Лучший способ понять монады — это начать их использовать. Нужно забить на монадические законы, теорию категорий, и просто начать писать код.
Написание кода на Haskell похоже на игру, в которой вы должны преобразовать объекты к нужному типу. Поэтому вам в первую очередь нужно понять правила этой игры. При написании кода вы должны четко понимать, какой тип имеет каждый конкретный кусок кода.
С обычными функциями все понятно. Если имеется функция типа «a->b», то подставив в неё аргумент типа «a», вы получите результат типа «b».
С монадами все не так очевидно. Под катом подробно расписано, как работать с do-конструкцией, как последовательно преобразуются типы, и зачем нужны монадные трансформеры.
1. Do-конструкция
Начнем с простого примера.
main = do
putStr "Enter your name\n"
name <- getLine
putStr $ "Hello " ++ name
Каждая do-конструкция имеет тип «m a», где «m» — это монада. В нашем случае это монада IO.

Каждая строчка в do-конструкции так же имеет тип «m a». Значение «a» в каждой строчке может быть разным.

Символ "<-", как бы, преобразует тип «IO String» в тип «String».
Если нам необходимо произвести в монаде некоторые вычисления, не связанные с данной монадой, то мы можем воспользоваться функцией return.
return :: a -> m a
main = do
text <- getLine
doubleText <- return $ text ++ text
putStr doubleText
Функция return заворачивает любой тип «a» в монадический тип «m a».

В данном примере, с помощью return выражение типа «String» преобразуется к типу «IO String», которое потом обратно разворачивается в «String». Как вариант, внутри do-конструкции можно использовать ключевое слово let.
main = do
text <- getLine
let doubleText = text ++ text
putStr doubleText
Вся do-конструкция принимает тип последней строчки.

Допустим, мы хотим прочитать содержимое файла. Для этого у нас имеется функция readFile.
readFile :: FilePath -> IO String
Как видим, функция возвращает «IO String». Но нам нужно содержимое файла в виде «String». Это значит, что мы должны выполнить нашу функцию внутри do-конструкции.
printFileContent = do
fileContent <- readFile "someFile.txt"
putStr fileContent
Здесь переменная fileContent имеет тип «String», и мы можем работать с ней, как с обычной строкой (например, вывести на экран). Обратите внимание, что получившаяся функция printFileContent имеет тип «IO ()»
printFileContent :: IO ()
2. Монады и монадные трансформеры
Я приведу следующую простую аналогию. Представьте, что монада — это пространство, внутри которого можно производить некоторые, специфичные для данного пространства, действия.
Например, в монаде «IO» можно выводить текст в консоль.

main = do
print "Hello"
В монаде «State» есть некоторое внешнее состояние, которое мы можем модифицировать.
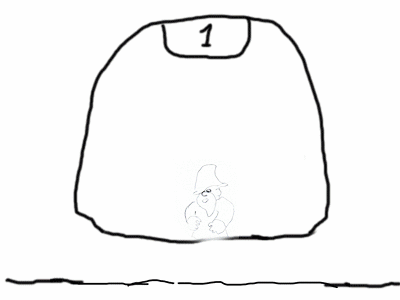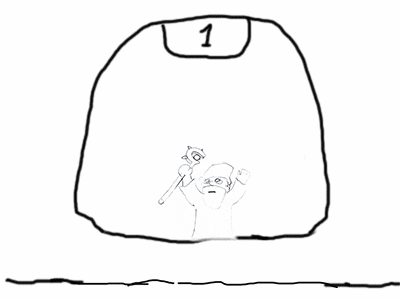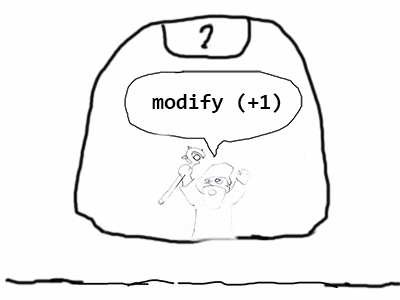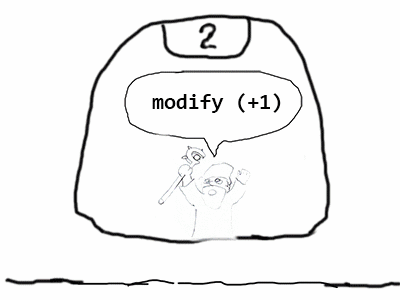
main = do
let r = runState (do
modify (+1)
modify (*2)
modify (+3)
) 5
print r
-- OUTPUT:
-- ((), 15)
В этом примере мы взяли число 5, прибавили к нему 1, умножили результат на 2, затем прибавили еще 3. В результате получили число 15.
С помощью функции runState
runState :: State s a -> s -> (a, s)
мы «запускаем» нашу монаду.

На монаду можно посмотреть с двух сторон: изнутри и снаружи. Изнутри мы можем выполнить некоторые, специфичные для данной монады, действия. А снаружи — мы можем её «запустить», «распечатать», преобразовать к некоторому немонадическому типу.
Это позволяет нам вкладывать одну do-конструкцию в другую, как в приведенном выше примере. Монада IO — это единственная монада, на которую нельзя посмотреть «снаружи». Все в конечном итоге оказывается вложенным в IO. Монада IO — это наш фундамент.
Приведенный выше пример имеет определенные ограничения. Внутри монады State мы не можем выполнять действия, доступные в IO.

Мы оказались «подвешенными в воздухе», потеряли связь с землей.
Для решения этой проблемы существуют монадные трансформеры.
main = do
r <- runStateT (do
modify (+1)
modify (*2)
s <- get
lift $ print s
modify (+3)
) 5
print r
-- OUTPUT:
-- 12
-- ((), 15)
Данная программа делает то же самое, что и предыдущая. Мы заменили State на StateT и добавили две строчки:
s <- get
lift $ print s
с помощью которых выводим промежуточный результат в консоль. Обратите внимание, операция ввода/вывода выполняется внутри «вложенной» монады StateT.
Здесь runStateT запускает монаду StateT, а функция lift «поднимает» операцию, доступную в IO, до монады StateT.
runStateT :: StateT s m a -> s -> m (a, s)
lift :: IO a -> StateT s IO a
Изучите внимательно, как последовательно преобразуется тип в данном примере.

Операция «print s» имеет тип «IO ()». С помощью lift мы «поднимаем» его до типа «StateT Int IO ()». Внутренняя do-конструкция теперь имеет тип «StateT Int IO ()». Мы «запускаем» её и получаем тип «Int -> IO ((), Int)». Затем мы подставляем значение «5» и получаем тип «IO ((), Int)».
Поскольку, мы получили тип «IO», то мы можем использовать его во внешней do-конструкции. Стрелочка "<-" снимает монадический тип и возвращает "((), Int)". В консоль выводится результат "((), 15)".
Внутри StateT мы можем менять внешнее состояние и выполнять операции ввода/вывода. Т.е. монада StateT не «болтается в воздухе», как State, а осталась связанной с внешней монадой IO.

Таким образом, в программе может быть куча монад, вложенных друг в друга. Некоторые из этих монад будут сцеплены друг с другом, некоторые — нет.
Надеюсь, моя аналогия помогла Вам взглянуть на вещи с новой точки зрения, и Вы сможете в будущем стать настоящим повелителем монад.

Комментарии (50)

devpony
04.03.2017 11:42+3Уж лучше вообще ничего не объяснять, чем объяснять всё некой магией, которая дана нам свыше и с помощью божественной силы может "поднимать" монады и "преобразовывать"
IO StringвString. Нужно понимать как работает твой инструмент, на какую математику он опирается, во что преобразуется do нотация, что такое монады и зачем вообще они нужны, а не просто бездумно их использовать. Иначе чем это лучше Карго-культа?
К тому же в статье всё изложено бегло и скомкано, не приведено никаких примеров. Статья рассчитана на абсолютных новичков, однако изобилует сложными терминами. Половина кода в мыльных картинках, половина не подсвечена. Не знаю, к чему стремился автор, но желанием помочь новичкам он точно не горел.
Вот пример как нужно объяснять монады новичкам, не теряя при этом важных деталей, не используя сложных терминов и не скатываясь в объяснение через магическую силу.

Tazman
04.03.2017 13:51+3Я с вами категорически не согласен. Я утверждаю, что новичок нуждается в «магии». Если перегружать новичка деталями, то это его еще больше запутает. Я сознательно упустил математическую строгость в пользу понятности.
Поэтому моя статья написана именно в таких терминах и именно на новичков она и рассчитана.
sshikov
04.03.2017 15:03+5Вообще гооворя, в монадах нет никакой магии. И незачем ее приплетать.
+1 к отсылке на видео (разве что я его смотрел на канале c9 от MS).
DmitryKoterov
05.03.2017 11:16+1Оффтопик, но я помню, что видео выше напомнило мне в свое время известную карикатуру «как нарисовать сову»: http://www.yaplakal.com/forum2/topic286982.html
Причем фальшивые поддакивания и хмыканья человека за кадром только укрепляли данное впечатление.
Практические примеры нужны, практические.
sshikov
05.03.2017 11:33+2Я тут могу сказать только одно — у монад есть две стороны. Одна — это чистая математика. И Бекман объясняет именно ее, причем на совершенно тривиальном уровне (ну, не считая английского языка изложения). И я настаиваю, что в ней нет никакой магии, если опять же посмотреть того же Бекмана. Это упрощенный вариант описания, но на мой взгляд — совершенно достаточный.
А практические примеры — это совершенно другая сторона, чисто программистская и прикладная. Где монады применяются как способ композиции программы из частей, где части — это функции. И это по сути тоже весьма несложная штуковина, если математическую ее часть понимать на уровне того же Бекмана.
>Практические примеры нужны, практические.
На мой взгляд в этой статье примеры вполне себе практические. Я только не согласен, что они совсем-совсем для начинающих. Можно было и попроще придумать наверное.

sshikov
05.03.2017 14:52+2Что до практических примеров, то спрошу так: неужели сегодня кому-то не хватает например практических примеров применения монады Option/Maybe? Ну скажем вот?. Это, на минутку, 2008 год.
Скажем, у вас есть функция, которая достает из базы какую-либо сущность. Дальше с ней нужно что-то сделать, некая последовательность обработки. При этом сущности в базе может и не быть.
Какие у нас есть варианты?
1. Проверяем после каждой функции «код возврата», который может нам говорить, что в базе ничего не нашли. Или была ошибка. Куча if в коде.
2. Выкидываем из функции поиска exception. Получаем типичный результат в стиле Java, который я приводить не буду, ибо их навалом.
3. Заворачиваем результат в Maybe. Дальше работаем с ним при помощи map/flatMap и т.п., так что вся последовательность пишется так, как будто у нас всегда есть результат.
Хотя на вкус и цвет, как говорится, все фломастеры разные, все же практическая польза тут обычно достаточно очевидна. Монады это, в частности, способ организации вычислений. В том числе — и в таких вот случаях. Который обеспечивает некоторые преимущества (и наверное, имеет некоторые недостатки), а именно более легко осуществляется композиция кода из частей.
Таких примеров — их в сети и так уже тысячи.
DmitryKoterov
05.03.2017 19:36+1Ну слушайте, Option и Maybe — это же вообще не о том (с практической точки зрения; с теоретической — так вышло, что одно и то же, но легче от этого особо не становится). Речь-то про IO и побочные эффекты, как с с ними обходиться в чисто функциональном языке. А у Option/Maybe — какие побочные эффекты?

sshikov
05.03.2017 20:08Мне бы не хотелось вот так на ночь отвечать на этот вопрос длинно, поэтому попробую спросить у вас — а как по-вашему, в чем состоит суть монады IO? Ну то есть, как же именно она обращается с побочными эффектами, скажем, файлами, сокетами, базами данных и прочим? Почему вы думаете, что это не о том?
Мой простой ответ: это все ровно о том же. По крайней мере с точки зрения «снаружи от самой монады».

sshikov
05.03.2017 20:12Вы ссылочку-то почитайте, которую я кинул. Там в разделе «Что общего» как раз неплохо описано, что же именно общего у IO и Maybe, например. И вообще.
Nakosika
04.03.2017 12:38К стати, многие не знают, но optional, steam в java 8 — это монады. А еще есть rxjava...

sshikov
04.03.2017 15:06Строго говоря — не совсем. Были разговоры, что разработчики как раз пытались уйти от того, чтобы делать optional монадой. Когда им резонно говорили, что все равно в итоге получится оно — не верили. В итоге сделали пусть и кривую, но все равно монаду.

Sirikid
05.03.2017 01:21Монады связаны некой общей сущностью — классом типов, а
OptionalиStreamнет.Nakosika
05.03.2017 02:30+1Ну конечно есть различия. Если кому интересно вот тут подробнее: https://dzone.com/articles/whats-wrong-java-8-part-iii
Optik
05.03.2017 11:47+1Монада определяется только поведением. Класс типов же нужен для абстрагирования.

Sirikid
05.03.2017 12:42+1Да, вы правы, я размышлял на этим и пришел к тому же выводу. Но разве не половина смысла монад в том, что можно писать функции абстрагированные от конкретной монады функции?
Optik
05.03.2017 14:34+2У монады смысл в том, что производится манипуляция не только со значением, но и с эффектом конкретной монады. То, что можно выделить интерфейс и в каких-то случаях абстрагироваться от конкретики, конечно прекрасно, но все же вторично.

sshikov
06.03.2017 09:57Я бы сказал, что это зависит от вашей цели. Невозможность абстрагироваться приводит к copy&paste при разработке кода очередной монады. Тому же кто ей пользуется — ему вообще все равно. Тех кто пользуется обычно намного больше.

funca
04.03.2017 18:43Спасибо за статью. Монады в программировании известны давно, но вне академических кругов не особо популярны на практике. Почему, как вы считаете?

Tazman
04.03.2017 20:35+2Мне кажется, проблема в системе типов. Система типов обычных языков, типа C#, просто не позволяет делать такие выкрутасы, которые позволяет система типов Haskell.
Допустим, есть класс типов Monoid
class Monoid a where mempty :: a mappend :: a -> a -> a
Я могу «эмулировать» его в C# с помощью интерфейса
interface Monoid<A> { A mempty(); A mappend(A a1, A a2); }
Затем я могу сделать instanse моноида для конкретного типа с помощью наследования
class IntMonoidInstance: Monoid<int> { int mempty(){ .. } int mappend(int a1, int a2) { .. } }
Но этот фокус не сработает для монады.
Класс типов монады объявлен как
class Monad m where return :: a -> m a (>>=) :: forall a b . m a -> (a -> m b) -> m b
Здесь m является не просто типом, как в случае с моноидом. Она является типом, параметризированным другим типом. Другими словами: * -> *.
Интерфейс для монады в C# должен выглядеть примерно так
interface Monad<M> where M: * -> * { M<A> return<A>(); M<B> bind<A, B>(M<A> a1, Func<A, M<B>> a2); }
Но C# со своей мощной системой типов не позволяет делать такие штуки. Я не могу объявить интерфейс, параметризированный типом, который параметризирован другим типом.
Любые реализации монады в C# все равно останутся недо-монадой.
sshikov
04.03.2017 22:51>Любые реализации монады в C# все равно останутся недо-монадой.
Это все-же не совсем так. Вы не можете сделать generic монаду, параметризованную. Это и для java кстати верно. Но любой конкретный экземпляр монады с фиксированными типами будет на практике вполне полноценным.
Tazman
04.03.2017 23:03+1Ну да. Можно реализовать частный случай. Но написать обобщенную функцию для произвольной монады, как в hakell, уже не получится. Например, не получится написать функцию типа
filterM :: Monad m => (a -> m Bool) -> [a] -> m [a]
negroid_gg
05.03.2017 23:21+3Вот есть такой пример .Net библиотеки https://github.com/louthy/language-ext, где кодогенерацией решается проблема невозможности написать обобщенную функцию для произвольной монады. Но, правда, чем больше ею пользуюсь, тем больше мыслей о том, что лучше уже перейти на F# и писать меньше кода.

sshikov
04.03.2017 22:54Монады не особо популярны? А ничего, что например jquery ($) это тоже монада? Ну да, со многими ограничениями, ну да, не совсем полноценная, почему так — вам уже ответили. Но тем не менее — это монада, самая настоящая. Вы считаете, что javascript, а точнее jquery — это академические круги? )))
Я вам больше скажу — в последние несколько лет это не просто популярно, это уже даже где-то модно.
funca
05.03.2017 03:29+1jquery ($) это тоже монада
докажите
sshikov
05.03.2017 10:10А вы посмотрете внимательно, что $ делает. У вас есть дерево DOM, состоящее из разнородных нод. Элементы, атрибуты, и прочее и прочее. $ позволяет вам применять к нему разного рода функции, для фильтрации и трансформации этого дерева, таким образом, как будто это простые строки, например. Т.е. применять скажем функции string->string к нодам DOM. Ничего не напоминает?
И если вы поищете — то найдете тут аналогии для flatMap например. Причем легко.
Т.е. по сути, $ это полноценный функциональный вариант монады в ее программистском стиле (программистском — потому что есть еще строгое математическое определение монады в теории категорий).
Да, если строго подходить — то можно долго придираться, что для $ мы не можем доказать, что законы выполняются, что система типов языка не позволяет написать монаду раз и навсегда, как это выше описано на примере C#. Но фактически — это самая натуральная монада.pawlo16
05.03.2017 10:56-1Не надо пороть гуманитарную чушь с умным видом. Монада — это мноноид в категории эндофункторов. Это на минутку ЕДИНСТВЕННОЕ ОПРЕДЕЛЕНИЕ монады. О том, каким образом класс типов Monad в Haskell представляет абстракцию этого ОПРЕДЕЛЕНИЯ, написано много и подробно. Вот и обоснуйте ваше утверждение про jQuery исходя из данного ОПРЕДЕЛЕНИЯ. Но вы не сможете, поскольку никакого отношения эта ваша жиквери к монадам не имеет, суть обычная обёртка над низкоуровневыми данными, по понятиям дурачка Фаулера — адаптер :)

sshikov
05.03.2017 11:13Продолжайте дальше жить в мире своих абстракций.
pawlo16
05.03.2017 14:18Ок, докажите что ваш мир реальней, приведя "программисткое" определение и показав, что жиквери ему соответствует. Либо признайте, что ляпнули не подумав.

sshikov
05.03.2017 14:26-1Гы. Открываем например википедию:
— Монада — термин в функциональных языках программирования.
— Монада — термин в теории категорий.
>Это на минутку ЕДИНСТВЕННОЕ ОПРЕДЕЛЕНИЕ монады.
Чё? Где-же единственное, когда вот их уже два (не считая еще трех, которые философского и прочих смыслов)? Вот идите, и сами себе доказывайте, что хотите.pawlo16
05.03.2017 15:22Продолжаем гнать дурочку? :-) не прокатит.
В статье википедии, на которую вы ссылаетесь, никакого "программистского" определения монады к сожалению для вас нет, там про Monad из Haskell.Вы не удосужились прочесть материал прежде чем ссылаться на него, ограничившись заголовком. Если уж заикнулись про википедию, покажите, какое отношение имеет жиквери к материалу из этой статьи.
Извините, но это не я, а вы утверждали тут что жиквери — монада. Так что сперва обоснуйте своё утверждение ЛОГИЧЕСКИ (о доказательствах я уже молчу), а потом рассказывайте кому куда идти и что делать.

sshikov
05.03.2017 15:50>В статье википедии, на которую вы ссылаетесь, никакого «программистского» определения монады к сожалению для вас нет
Может кому-то язык не родной?
«Мона?да в функциональном программировании — это абстракция линейной цепочки связанных вычислений. „
Итак, определение — не единственное. У меня уже все прокатило.pawlo16
05.03.2017 16:41А линейная цепочка связанных вычислений — это что такое? Является ли, например, функция абстракцией линейной цепочки связанных вычислений, и если не является, то почему? И какое отношение к этому имеет jquery?

funca
05.03.2017 16:08+1Вы пытаетесь убедить, а не доказать.
для $ мы не можем доказать, что законы выполняются
если так, $ не монада. для монад законы выполняются.
sshikov
05.03.2017 16:38+1Так, стоп, стоп. Давайте вернемся немного к началу. Я отвечал на ваш же вопрос, цитирую:
>Монады в программировании известны давно, но вне академических кругов не особо популярны на практике.
Суть моего замечания была в том, что соответствующие технологии и понятия (взятые из теории категорий, ясное дело) лежат в основе например $. То есть не просто популярны, а очень популярны. Вот в этом я и пытаюсь вас убедить.
>для $ мы не можем доказать, что законы выполняются
Я не просто верю, я практически знаю, что это так и есть. И что?
Начнем с того, что у $ весьма развесистое API, и тут нет прямого соответствия в виде «вот это bind, а вот это return». Более того, в языках типа javascript было бы глупо ожидать, что монада будет выглядеть как в хаскеле.
Ответьте, вот вам зачем монадические законы? На мой взгляд, они нужны исключительно для того, чтобы композиция работала правильно (а в идеале — чтобы это еще и статически проверялось). Но это далеко не всегда нужно, и далеко не всегда возможно (в конкретном языке).
Иными словами: если оно ходит как монада, крякает как монада, и плавает как монада — это монада и есть. Это такой вот прагматический подход, и именно таким образом монады уже давно и широко применяются налево и направо.
funca
06.03.2017 00:05+1
Ответьте, вот вам зачем монадические законы? На мой взгляд, они нужны исключительно для того, чтобы композиция работала правильно (а в идеале — чтобы это еще и статически проверялось). Но это далеко не всегда нужно, и далеко не всегда возможно (в конкретном языке).
Я просто поинтересовался причинами непопулярности монад. «это далеко не всегда нужно, и далеко не всегда возможно (в конкретном языке)» — вполне веский аргумент. Для композиции есть уйма других способов.
sshikov
06.03.2017 09:50Я боюсь вы не так поняли эту фразу. Далеко не всегда нужны монады? Ну это и так очевидно. Но я имел в виду, что далеко не всегда нужно формальное доказательство того, что законы монад соблюдаются. Это нам гарантирует правильность, но далеко не всю правильность, поэтому без этого вполне можно практически обходиться.
>Для композиции есть уйма других способов.
Ну да, есть. Но прям таки и уйма? Сможете назвать скажем четыре? )))
И потом, монады — один из достаточно удобных и проверенных.
funca
07.03.2017 00:42далеко не всегда нужно формальное доказательство того, что законы монад соблюдаются. Это нам гарантирует правильность, но далеко не всю правильность, поэтому без этого вполне можно практически обходиться.
тут вроде напрашивается другой вывод, что без соблюдения законов — которые гарантируют правильность, и то не всю — ни о какой правильности вообще не может быть и речи. $ это неправильный пример неправильной монады, так что-ли по-вашему?)
Ну да, есть. Но прям таки и уйма? Сможете назвать скажем четыре? )))
https://en.wikipedia.org/wiki/Software_design_pattern
sshikov
10.03.2017 14:46>без соблюдения законов — которые гарантируют правильность, и то не всю — ни о какой правильности вообще не может быть и речи.
Не без соблюдения законов, а без формального доказательства их соблюдения.

Vitter
10.03.2017 01:54+2Ответьте, вот вам зачем монадические законы?
Выполнение монадических законов гарантирует, что вы вы получите то, что ожидаете при использовании монадических функций.
Не, вы конечно можете переопределить, что "+" это "-", но только при использовании "+" вас ожидают неожиданные результаты вычислений

Sirikid
05.03.2017 00:41+3Не буду ничего говорить про магичность/немагичность монад и трансформеров, но вот do-нотация точно синтаксический сахар, почему бы не объяснить её так?

sshikov
05.03.2017 10:01+2Именно так. Некая «магия» или если угодно, сахар есть именно в do нотации, а не в самих монадах. То что они тут местами перемешаны — вовсе не упрощает дело.


redbeardster
Спасибо, пишите еще. Нашелся бы добрый человек, который запилил бы курс по Coq — было бы совсем прекрасно.
Tazman
Я думал об этом. Coq я люблю. Только эта тема не очень востребована.
ymn
Курс по Coq уже давным давно запилен и называется «Software Foundations». Альтернативный курс называется «Certified Programming with Dependent Types».
Лучше ничего нет.