Движение при полном отсутствии вязкости проявляется во многих впечатляющих эффектах: сверхтекучий гелий легко протекает через самые узкие щели и трещины, способен бесконечно течь по кругу(**) и вытекать из сосуда через тончайшую жидкую пленку, налипшую на его стенки. Все эти явления – примеры крупномасштабных квантовых эффектов.
В недавней теоретической статье был рассмотрен вопрос: можно ли плавать в сверхтекучей жидкости? Иными словами, может ли гипотетический пловец, двигая руками и ногами, создавать силу тяги, позволяющую ему разгоняться или замедляться, не задействуя силы вязкого трения?
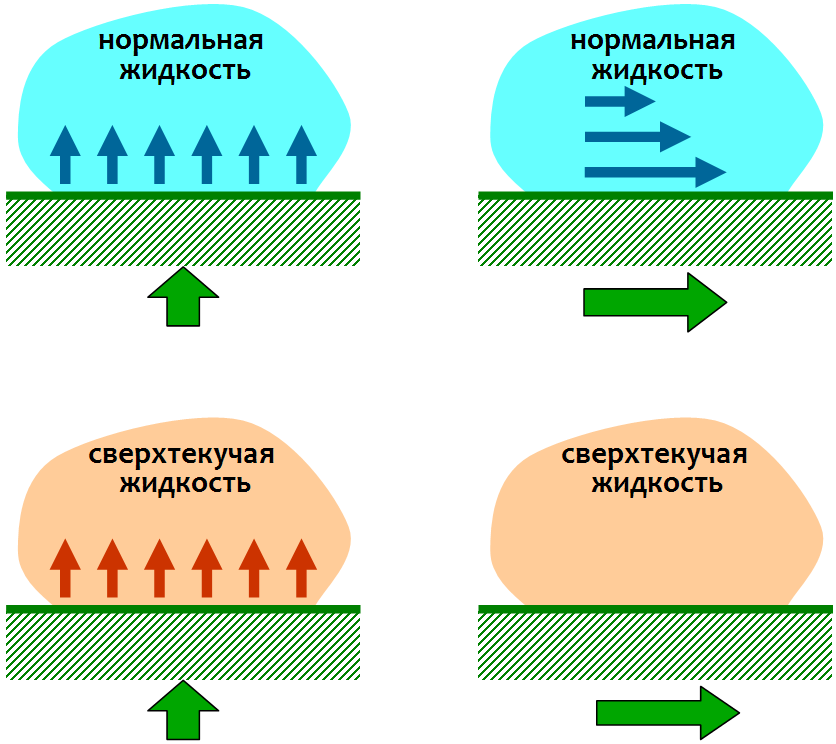
Осознать нетривиальность ответа на этот вопрос можно, рассматривая поведение нормальной и сверхтекучей жидкостей при взаимодействии с телами. Как показано на рисунке, нормальную жидкость можно заставить двигаться, как толкая ее поверхностью твердого тела, так и увлекая ее за собой за счет сил вязкого трения. В сверхтекучей жидкости последнее не получится: трение в ней отсутствует, и ее можно только толкать, что, как мы увидим, делает невозможным некоторые способы плавания.
Для анализа общих принципов физических явлений принято рассматривать простые модели «сферических коней в вакууме». Обсуждаемая статья не является исключением: в ней были рассмотрены двухтельный и трехтельный модельные «пловцы», представляющие собой два и три эллипсоида, соединенных «суставами». Пловцы могут двигать своими эллипсоидами, сгибая и разгибая суставы. Если у пловца получится отталкиваться от окружающей жидкости, он создаст силу тяги и начнет двигаться.

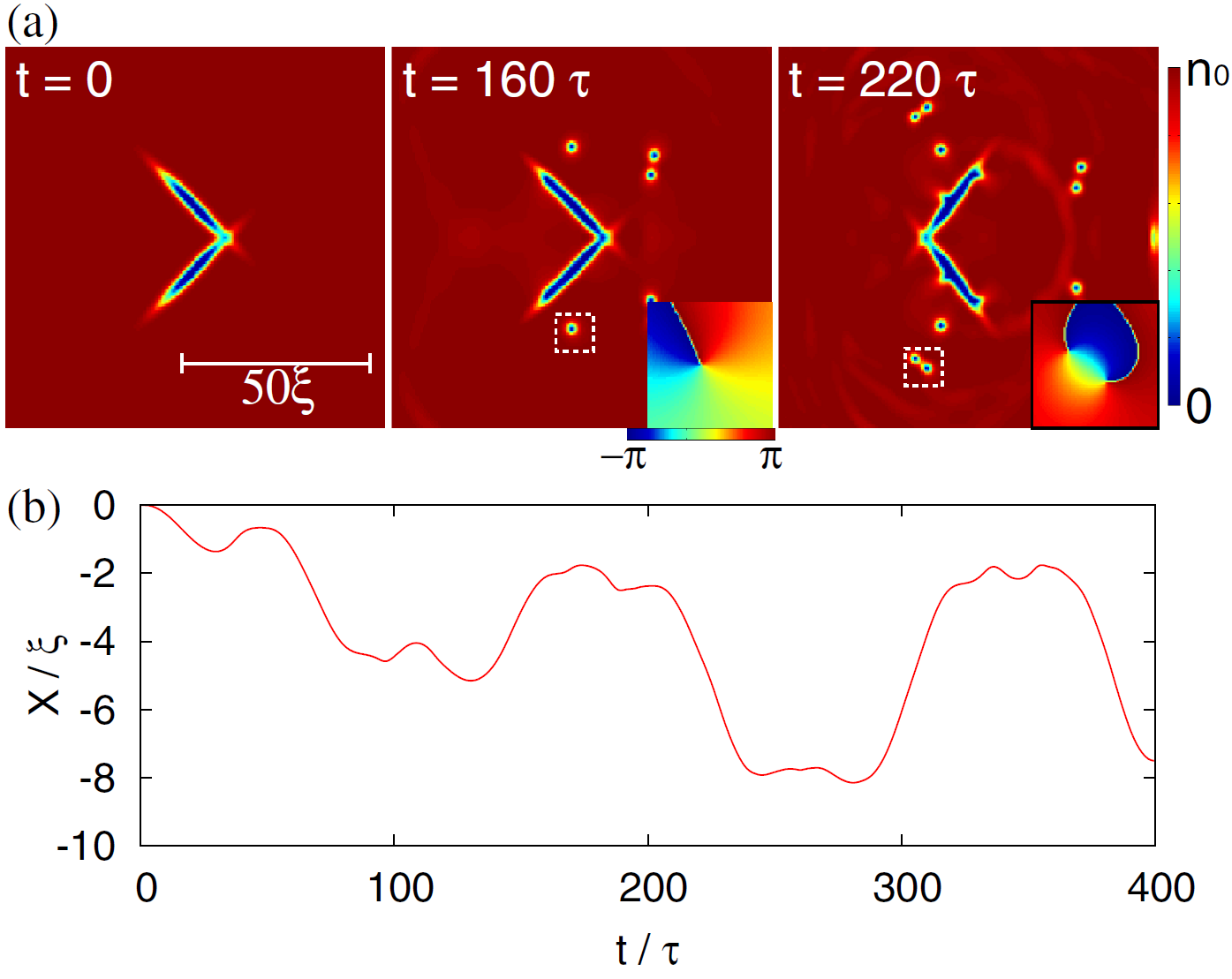
Двухтельный пловец похож на двустворчатого моллюска и может пытаться плыть, периодически изменяя угол между своими эллипсоидами подобно машущей крыльями бабочке. Однако расчеты показывают, что плыть у него не получится: при взмахах пловец перемещается вперед и назад, но в среднем остается на месте (здесь можно посмотреть видео его незамысловатых движений).

Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды двухтельного пловца.
Внизу: координата пловца как функция времени.
Можно провести параллели между этим результатам и теоремой Пёрселла о морском гребешке (Purcell’s scallop theorem). Эта важная теорема теории плавания гласит, что двустворчатый моллюск, медленно открывающий и закрывающий свою раковину в вязкой жидкости, не будет никуда плыть, коль скоро его движения будут обратимы во времени. Последнее означает, что периодические открывания и закрывания створок раковины не меняют свой вид при запуске времени в обратном направлении (можно представить себе видеоролик, выглядящий просмотре задом наперед точно так же, как при нормальном воспроизведении). В нашем случае жидкость не имеет вязкости, и работает не сама теорема Пёрселла, а ее аналог для сверхтекучей жидкости.

Рисунок из доклада Эдварда Пёрселла (лауреата Нобелевской премии по физике в 1952 году).
Ситуация меняется, когда двухтельный пловец начинает размахивать своими эллипсоидами с большей частотой. Если скорость их движения превышает скорость звука в жидкости, начинают испускаться звуковые волны и вихри(***). Эти возбуждения уносят с собой некоторый импульс, который, за счет отдачи, заставляет пловца двигаться. На рисунке видно, что в этом случае его координата хоть и колеблется, но с течением времени в целом уменьшается, а это значит, что пловец движется справа налево. После десяти колебаний (справа от пунктирной линии на графике) взмахи створками прекращаются, и пловец продолжает двигаться по инерции (видео).

Можно попробовать и другой тип движения пловца, когда его створки смыкаются и раздвигаются не только в правом направлении, а попеременно в двух направлениях. Такие симметричные движения похожи на взмахи крыльев бабочки. Расчеты показывают, что при этом возбуждается много квантованных вихрей (они видны на рисунке как маленькие кружочки), но, в целом, плавание не очень эффективно. Причина в том, что возбуждается примерно одинаковое количество вихрей, движущихся как вправо, так и влево, и уносимые ими импульсы в значительной мере компенсируют друг друга (видео).
Рассмотрим теперь трехтельного пловца. Перед двухтельным у него есть важное преимущество: он может извиваться, совершая змеевидные движения, которые не переходят сами в себя при обращении времени. А значит, теорема Пёрселла к нему неприменима, и он должен плыть даже при медленных движениях. Приведенные на рисунке расчеты подтверждают эту догадку: при извивающихся движениях пловец уверенно продвигается по горизонтали, при этом немного смещаясь и по вертикали (видео).
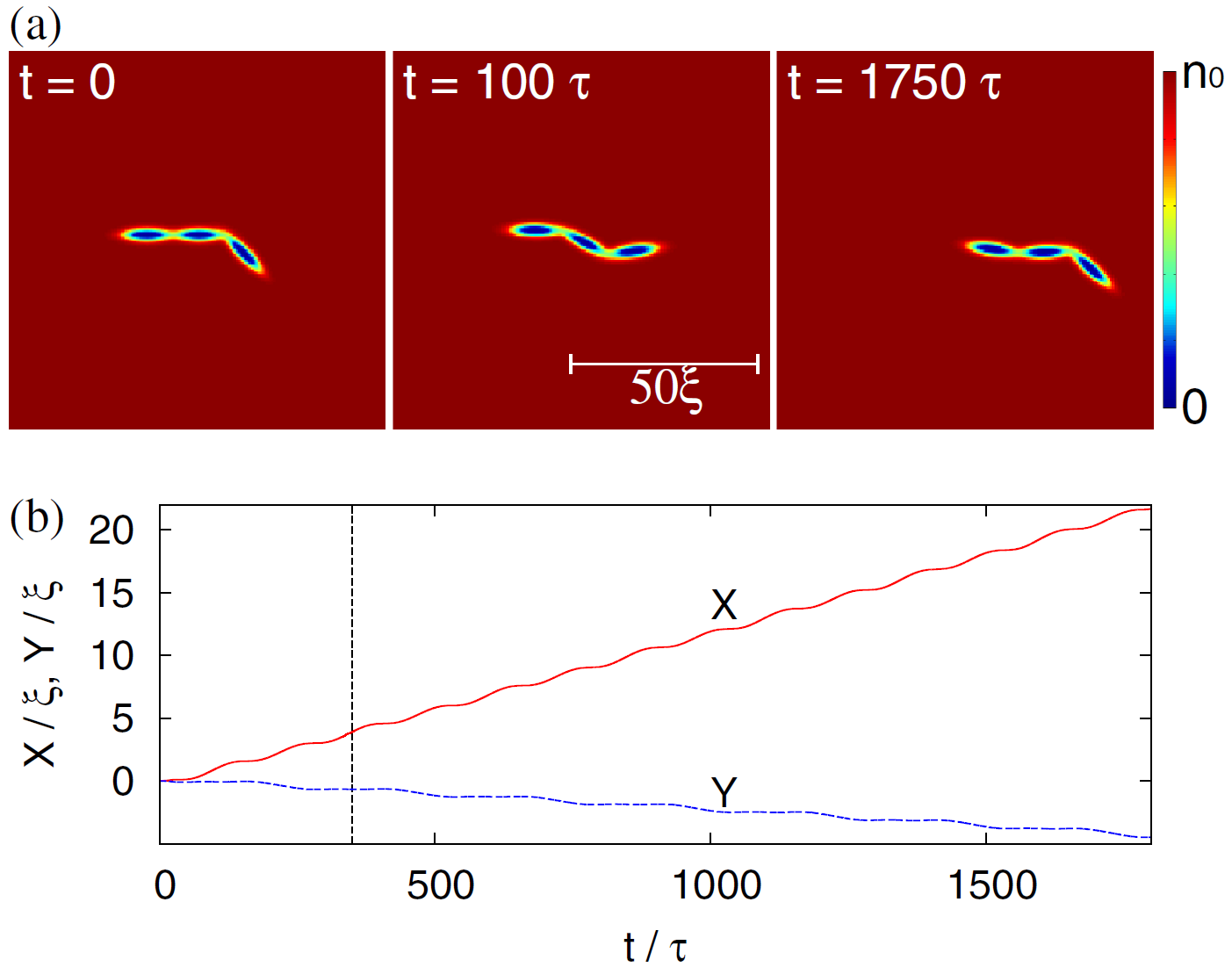
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды трехтельного пловца.
Внизу: горизонтальная (X) и вертикальная (Y) координаты пловца как функции времени.
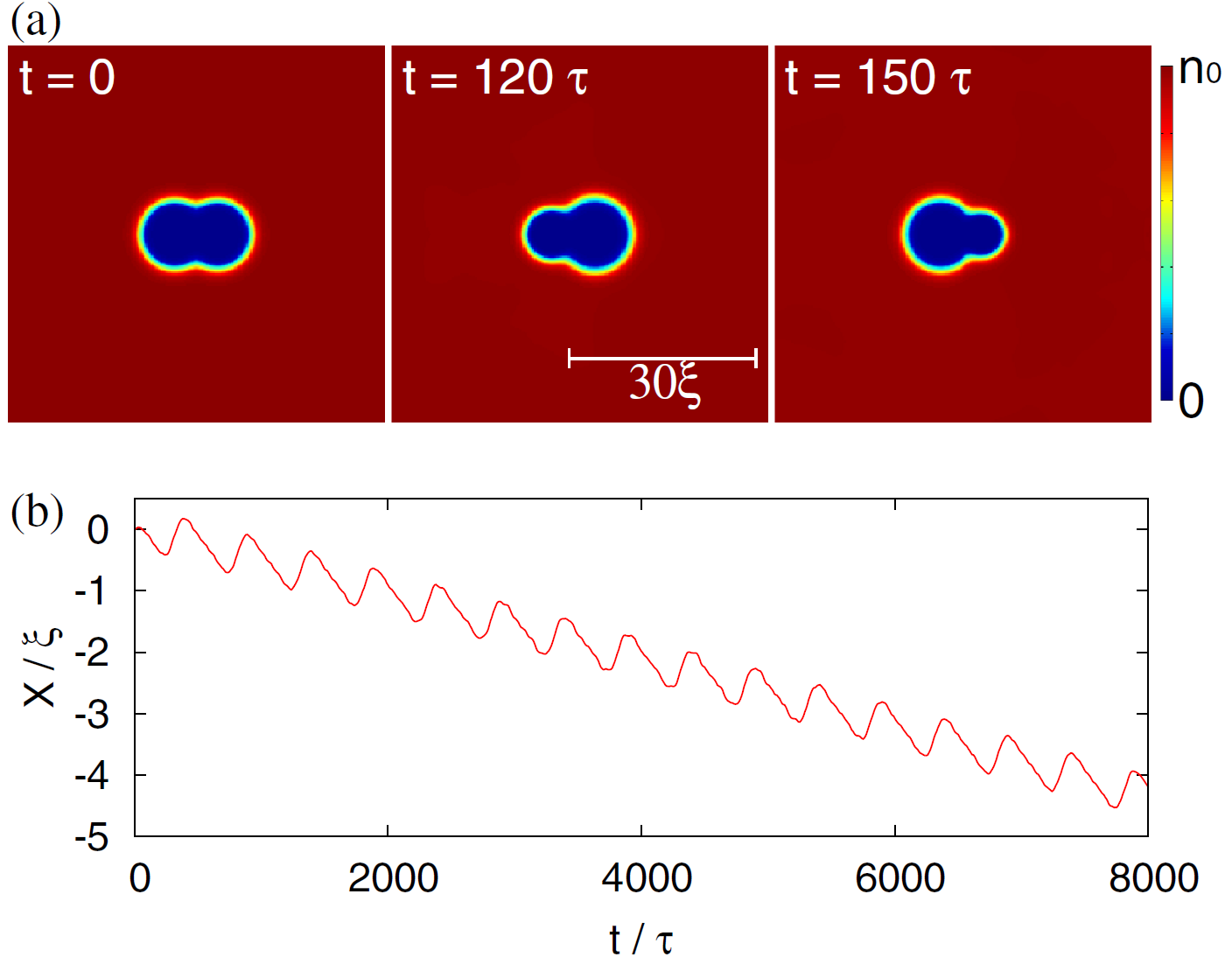
Какое применение можно найти полученным результатам? Казалось бы, задача о плавании в сверхтекучей жидкости не особо актуальна на практике, но есть одна область, где она может быть полезной. В последнее время активно развиваются эксперименты с бозе-конденсацией и сверхтекучестью ультрахолодных атомных газов, с которыми связывают большие планы по созданию квантовых симуляторов, квантовых компьютеров и экспериментальному моделированию экзотических состояний материи. В таких системах можно создавать сгустки сверхтекучего газа одного вида, погруженные в сверхтекучий газ другого вида. Если мы сможем деформировать сгусток так, как нам нужно (а это можно делать с помощью лазерных лучей), то можно будет заставить этот сгусток плыть, отталкиваясь от окружающего газа. На рисунке показаны расчеты, демонстрирующие такую возможность: когда изменения формы сгустка не являются обратимыми во времени, ему действительно удается двигаться (видео).
Итак, мы видим, что плавать в сверхтекучей жидкости нужно с умом: теорема Пёрселла гарантирует, что мы не сможем плыть, если наши движения руками и ногами будут совпадать с самими собой при проигрывании в обратном направлении. Чтобы начать перемещаться, нам нужно будет либо двигаться быстрее звука (что проблематично), либо извиваться подобно змее, нарушив обратимость движений во времени. Эти выводы хорошо знакомы плавающим в вязкой жидкости микроорганизмам: для того, чтобы обойти теорему Пёрселла, им приходится использовать спирально вращающиеся жгутики, являющиеся аналогами рассмотренного здесь трехтельного пловца.
По материалам статьи:
Hiroki Saito, Can We Swim in Superfluids?: Numerical Demonstration of Self-Propulsion in a Bose–Einstein Condensate, Journal of the Physical Society of Japan 84, 114001 (2015).
(*)На самом деле, это не совсем так: любая реальная сверхтекучая жидкость может быть представлена как совокупность «нормальной» и сверхтекучей компонент (двухжидкостная модель), и нормальная компонента будет по-прежнему замедлять движущееся тело. Однако это не мешает сверхтекучей компоненте двигаться полностью без трения.
(**)На практике круговой поток сверхтекучего гелия может затухать, но не из-за вязкости, а за счет квантовомеханического процесса – проскальзывания квантованных вихрей. В экспериментах не наблюдалось никакого заметного затухания в течение 18 часов.
(***)Возникающие в сверхтекучей жидкости вихри – это не просто вихри наподобие маленьких торнадо, а квантованные топологические возбуждения. В отличие от обычных вихрей, они не могут просто исчезнуть за счет постепенного затухания потока.
Комментарии (80)

amarao
28.03.2017 17:09+1Если бы мне предложили такую задачу, то я бы решал её так:
1. Создадим сферическое тело с соплом и клапаном, сопло закрывающим по нашему желанию.
2. Добавим в него боковые симметричные отверстия с клапанами (симметрия: равномерно по окружности с шагом в 30 градусов, например).
3. Добавим внутри сферы поршень любого вида. (Если возникает вопрос о создании импульса из-за движения поршня, пусть он будет сферический надувающийся).
Принцип движения:
1) закрыть клапан сопла
2) Открыть боковые отверстия
3) Убрать поршень (сжать/сдуть), пока внутренняя поверхность не наполнится.
4) Закрыть боковые клапаны
5) открыть клапан сопла.
6) Вытеснить жидкость поршнем.
PhysRevB
28.03.2017 19:00+2А эти движения как раз будут несимметричными относительно обращения времени — при запуске времени в обратном направлении получится то же самое, но с переставленными местами 3-й и 6-й стадиями, т.е. последовательность операций не будет совпадать с исходной.

DrZlodberg
28.03.2017 19:14+2Не очень понял про симметричность. Допустим моллюск медленно раскрывает створки, а потом резко захлопывает. Получаем небольшую реактивную струю, которая толкает в противоположную сторону. Да, при раскрытии чуть смешается назад, но в целом должен двигаться вперёд ведь. Или я что-то упускаю?

PhysRevB
28.03.2017 19:24+2Если резко захлопывает, то теорема Пёрселла уже нарушается, она справедлива для очень медленных движений. Моллюску ее нарушить довольно просто, а вот на пространственных масштабах микроорганизмов это уже нереально, они не могут двигаться с достаточно большой для ее нарушения скоростью.

DrZlodberg
28.03.2017 20:06+3Ну т.е. плавать можно, если не создавать очень специфичных условий и не быть микроорганизмом, что из статьи не очень очевидно с учётом упоминания моллюска и рук-ног.

PhysRevB
28.03.2017 20:44+2Про моллюска и микроорганизмы — это рассуждения для вязкой жидкости, а в сверхтекучей жидкости макроскопические размеры не помогут, там придется захлопывать створки со сверхзвуковой скоростью.

DrZlodberg
28.03.2017 20:55+1Т.е. даже если возьмём предельный случай — мешок который сокращается (как у кальмаров например) — всё равно импульс получить не выйдет без сверхзвука?

PhysRevB
28.03.2017 21:04+2Если засасывать и выбрасывать воду через одно и то же отверстие, то, думаю, не получится. Будут просто колебания взад-вперед.

Tufed
29.03.2017 11:18Разница в силе. В обычной жидкости роль играет еще и размер сопла, но в вашем случае как-то так: засасывание воды производится медленно и дает небольшой импульс по движению назад (P=V*H*c). Выбрасывание воды происходит быстро и даёт существенно больший импульс по движению вперед (P2=V*H2*c2). где V — объем воды одинакова, H-сила всасывания, H2 сила выталкивания, c-время всасывания, с2-время выталкивания. Т.к. переменные H и с обратно пропорциональны только на некотором отрезке, а в дальнейшем при повышении силы H разница будет заметнее. Приведу пример для лучшего понимания: взяли объем V рядом, затратили E энергии, потом оттолкнули его сильнее и затратили E*2 энергии, в итоге импульс отталкивания выше чем импульс притягивания. Еще интереснее если брать как было выше объем сбоку, тогда назад отката не будет. Про запуск времени в обратном направлении забудьте, ересь какая-то. Нет такого способа чтобы время запустить в обратном направлении. Не придумали еще человеки и пока что не предвидится, смиритесь с этим…

PhysRevB
29.03.2017 12:55+1Невозможность движения таким образом доказывается строго — https://arxiv.org/abs/0909.3860
— но как это объяснить на пальцах, не очень понятно. В доказательстве ключевым моментом является то, что движение сверхтекучей жидкости является безвихревым, т.е. жидкость не может закручиваться.
Применительно к вашему примеру: если исходить из уравнения Гросса-Питаевского, описывающего движение сверхтекучего конденсата, то сгусток разогнанной жидкости, который вы создаете при выталкивании, не сможет уйти на бесконечность и унести с собой импульс. Возможно, из-за этого сгустка за кормой создастся область пониженного давления, которая потянет пловца назад и скомпенсирует реактивный импульс. Так или иначе, нужно рассматривать не только силу взаимодействия между стенками камеры и жидкостью во время выталкивания и засасывания, а всю динамику системы в целом, как это делается при строгом рассмотрении.
Обращение времени — это, конечно, мысленная операция, но очень важная и широко используемая в теоретической физике. Анализ поведения системы при обращении времени позволяет многое сказать о ее качественных свойствах. Хотя локально, в какой-то небольшой системе, в экспериментах удается обратить движение во времени (спиновое эхо, эхо Лошмидта), это используется как метод исследования квантовой динамики.
Tufed
29.03.2017 18:49Не пойму причем тут безвихревое свойство. Ну не может жидкость закручиваться и как-то я не вижу как это относится к обсуждаемой теме? Это как то помешает предложенной схеме движения? Если да то попрошу уточнить как именно.
1)Почему сгусток не сможет уйти в бесконечность я понимаю, т.к. сверхтекучесть это не нулевое сопротивление, а просто очень маленькое, настолько маленькое что им можно пренебречь в нашей системе отсчета. Применительно к бесконечности по расстоянию и времени естественно когда-нибудь этот импульс сгустка погасится. Но мне и не нужно это, мну нужно только оттолкнуться от него, а там пусть себе летит в бесконечность сколь угодно. 2) Варианты «возможно» не интересны.
Ок, мысленно обращать время мы умеем = это и есть теория. Но вот в экспериментах… не знаю ни одного эксперимента чтобы обратить движение во времени. Если знаете опишите его.
PhysRevB
29.03.2017 22:26Потенциальность течения жидкости используется в математическом доказательстве теоремы, запрещающей плавание за счет обратимых движений. Как именно это проявляется на языке действующих на тело сил — точно сказать не могу (выше высказал лишь свое предположение), здесь было бы хорошо провести моделирование, но с такой степенью детальности его, вроде бы, никто не описывал.
Сверхтекучесть — это как раз нулевая вязкость, а не просто очень маленькая.
Экспериментов по реализации эха Лошмидта довольно много, вот только один пример:
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.79.032324
А здесь есть большой обзор со множеством ссылок на эксперименты:
http://www.scholarpedia.org/article/Loschmidt_echo
Tufed
30.03.2017 10:42Не могу согласится с вашей информацией о нулевой вязкости, вики мне говорит обратное: На сегодняшний день установлено, что коэффициент вязкости у гелия-II меньше 10^?12 Па·с, в то время как у гелия-I вблизи температуры 4,22 К этот коэффициент имеет величину порядка 10^?6 Па·с — это не ноль, хотя и очень маленькое значение.
Я не профессиональный ученый, а просто люблю физику и у меня были замечательные учителя. Я искренне уверен что любой физический процесс или явление можно объяснить простым языком доступным для понимания обычному школьнику, а уж тем более образованному человеку. т.к. вы не можете/не желаете отвечать на мои вопросы прямо и постоянно используете уловки чтобы перевести тему на то что к теме обсуждения не относится, то считаю дальнейшую дискуссию не продуктивной. Особенно меня радует эхо Лошмидта, которое я рассматривал весь вечер на приведенных вами ссылках и я искал информации больше, в надежде развеять сомнения в моих неполных знаниях или неполном понимании предмета. Но не вижу в экспериментах доказанного обращения во времени, только причинно-следственные связи и возможность вернуть объекты исследования в исходные позиции/состояния, пусть и на микро-уровне. Хотя там настолько усложнено и изобилует новыми для меня терминами, что читать и понимать это оказалось очень долго и тяжело.
PhysRevB
30.03.2017 11:01Теоретически вязкость нулевая, эксперименты показывают, что она не превышает какую-то очень малую величину — здесь нет противоречия (x=0 и x<10^-12 друг другу не противоречат). Гелий II это сверхтекучий гелий, а гелий-I это обычный жидкий гелий.

koderZ
29.03.2017 22:29Получится, при выбрасывании жидкости, импульс будет более направленным чем при ее всасывании

tiger847
29.03.2017 22:29+1И ваше решение бы отвергли потому, что вы используете реактивную тягу. а статья, вообще-то, была про гребной движитель. Простейший.

gerahmurov
28.03.2017 17:31+2А если рассматривать пловца-человека, то получится ли у него плыть в сверхтекучей жидкости, или жидкость начнёт сразу заливаться в лёгкие? Т.е. как только человек войдёт в воду, то сразу начнёт утопать.

amarao
28.03.2017 17:33+11Если мы говорим про жидкий гелий, то у «человека-пловца» будут более экстренные проблемы, чем посторняя жидкость в лёгких.
Например, температура окружающей среды ниже температуры замерзания кислорода.
Hayate
28.03.2017 17:37+5Можно жиром намазаться перед плаваньем.

amarao
28.03.2017 17:42+8Я попытался было попробовать посчитать насколько медленее будет остывать тело при перепаде температур в 300К, но быстро сдался — операторы Лапласа не для меня.
Зато у меня есть простая аналогия: с точки зрения теплопереноса направление не важно. Насколько хорошо защитит жировая плёнка тело при погружении в жидкость при температуре 300 градусов цельсия?
Мне кажется, это называется «фритюр». В отношении холода аналогично, только в обратную сторону.
APLe
28.03.2017 18:25+2Тут надо учесть ещё, что на поверхности тела жидкий гелий будет испаряться, образуя газовую прослойку между телом и жидкостью.

donvictorio
28.03.2017 22:36+7Но недолго. Где-то пару минут. Потом тело достигнет температуры гелия и пловцу придётся переходить на квантовые методы существования.

dmitry_dvm
29.03.2017 12:26+1Надо просто барахтаться но сверхзвуковой скоростью, тогда не замерзнешь.
igruh
28.03.2017 18:11+2Акваланг, термокостюм и много-много пенопласта для поплавка, учитывая плотность жидкого гелия.

Lachezis
28.03.2017 18:47+1В пенопласте много воздуха, он уменьшится в объеме при охлаждении и потонет.

vanxant
28.03.2017 19:22+1Вместо поплавка можно взять жесткий спасательный круг. Даже если воздух внутри него замерзнет до твердого состояния, масса этого воздуха не изменится, а значит сила Архимеда тоже.
Хотя конечно воздух лучше заменить на водород или хотя бы гелий.
Lachezis
28.03.2017 19:25+1Главное не забыть оставить урановый лом дома.

sevikl
28.03.2017 20:07+3урановый лом главное в поезд не брать

IvUyr
29.03.2017 23:19Представил себе ртутный унитаз… :-)
igruh
28.03.2017 20:16Вы недооцениваете пенопласт, многие сорта выдерживают. Есть ещё аэрогель. А вот привязать к себе кубометр водорода и выдыхать на него часть кислорода… Что-то в этом плане не то.

vanxant
28.03.2017 21:56+2Трюк в том, что если взять достаточно большой спасательный круг с водородом, в жидкий гелий можно и не лезть, летая немного над ним…
EnigMan
29.03.2017 17:13В жестком спасательном круге в таких условиях и водород не нужен. При достаточной жесткости круга самое эффективное откачать из него все газы вообще.

Kelt_Rivera
28.03.2017 17:49+1Как-то я плавал в грязи в
лужевулкане. Плыть там было проблематично: гребок рукой продвигает вперед, возвращение в исходную позицию продвигает назад, в итоге стоишь на месте. Нужна такая же статья, но для очень вязкой жидкости.
PhysRevB
28.03.2017 19:06+3Про вязкую жидкость как раз есть подробное рассмотрение в упомянутом докладе Пёрселла (на английском, к сожалению).
По сути, вы на себе испытали то, что чувствуют плавающие в воде микроорганизмы. На их пространственных масштабах вода ведет себя как предельно вязкая, не обладающая инерцией жидкость. И для того, чтобы в такой жидкости передвигаться, нужно вращать спиральным жгутиком, а грести руками бесполезно.

impetus
28.03.2017 19:42+2В очень вязкой у человека всегда есть поверхность с проносом руки поверху. напр в принципе можно «плыть» по песку.

Kelt_Rivera
29.03.2017 10:41Вот именно так я и сделал потом :) там ещё и плотность была очень высокая: при всём желании я не мог опуститься глубже. Можно было даже плавать на спине, подняв ноги над поверхностью...
Vjatcheslav3345
29.03.2017 18:34Интересно — тогда почему пострадавшим, попавшим в зыбучие пески, либо болото или смоляные ямы — не советуют в нём шевелиться, а не то что плавать?..
С другой стороны — в грязевой луже Вы испытали то, что чувствовали всякие динозавры и мамонты как раз перед тем, как скрыться на миллионы лет с дневной поверхности.
Kelt_Rivera
29.03.2017 23:15Интересная аналогия :D но, в отличии от диназавров я, слава богу, выжил. Да и не я один. Место-то было туристическим, там люди непрерывным потоком плавали и вылазили из грязи. А по-поводу песков и болота: возможно, там плотность меньше плотности тела, вот и такая разница

Browning
01.04.2017 20:16+1Зыбучий песок — другая история. Он не просто вязкий, он — неньютоновская жидкость. В нём чем быстрее движешься, тем он твёрже.

dom1n1k
28.03.2017 18:18По-моему, вполне очевидно, что отталкиваться от такой жидкости можно, поскольку ее удерживает на месте, помимо вязкого трения, еще и инерция.

eMarchenko
28.03.2017 18:47оттолкнуться можно, но как это сделать несколько раз? если возвращаться в исходную позицию, то см. т. Пёрселла.

dom1n1k
28.03.2017 19:46+1А в чем проблема? Грубо говоря, при отталкивании весло ставится поперек движения, а при его возврате — вдоль.

PhysRevB
28.03.2017 21:05-1Наверное, так тоже можно плыть, но в сверхтекучей жидкости это будет гораздо менее эффективно.
igruh
28.03.2017 21:38+1Мне кажется, что Вы перевели материал, но не углубились в суть явления. Грести можно и вантузом туда-обратно за счёт перераспределения импульса вдоль и поперёк движения. В статье рассматривается совсем уж сферический конь в вакууме — возвратно-поступательные движения без извлечения из среды… Хорошо, я первый: прошу либо по сути, либо, блин, наконец, смешно!

PhysRevB
28.03.2017 22:39-1При возвратно-поступательных движениях вантузом в сверхтекучей жидкости вы не поплывете, если только не будете двигать им быстрее скорости звука. Это доказывается в виде теоремы. Собственно, это и есть суть статьи: чтобы плыть, нужно совершать не возвратно-поступательные движения, а более сложные, не превращающиеся сами в себя при обращении времени.
Описанные выше движения веслами в эту категорию попадают, но чтобы количественно оценить их эффективность, нужно проводить расчеты. Так-то качественно понятно, что они будут менее эффективными, чем в нормальной жидкости.
Camill
29.03.2017 10:50Движения вантузом вполне могут быть несимметричны, если при движении «от себя» его диаметр будет шире, чем при обратном движении, на котором он будет слегка сжиматься. Представьте себе зонтик в воздухе, который вы болтаете туда-сюда.

NINeOneone
28.03.2017 18:59А не слишком ли это все напоминает газы? Я конечно не физик, но ведь они ведут себя практически так же. Поправьте, если не прав, но сходу не придумал никаких существенных отличий. Может стоило просто на газы посмотреть?

PhysRevB
28.03.2017 19:09+1Ну это все гидродинамика, она общая для газов и жидкостей. Различия лишь в количественных характеристиках — газы менее плотные и легче сжимаются, — а уравнения одни и те же. И сверхтекучими бывают как жидкости, так и газы.

vanxant
28.03.2017 19:15+1Уравнения Навье-Стокса для жидкостей, газов и плазмы одинаковые. Ну, в смысле, закорючки в них одинаковые, но скрываются под этими закорючками разные коэффициенты и прочие там числа Рейнольдса. Но есть одно важное отличие: невырожденные газы сжимаемы, а жидкости обычно нет.

Kelt_Rivera
29.03.2017 10:49Только сферические жидкости в вакууме несжимаемы (а.к.а малые возмущения вроде звука по ним распространяются мгновенно на любые расстояния). Просто скорость звука в воде значительно выше скорости звука в воздухе (что-то вроде 1500м/с, если я не ошибаюсь). Редко какие тела могут двигаться в воде с такой скоростью :) поэтому для большинства расчётов та же вода принимается несжимаемой. И, кстати, для несжимаемой жидкости-таки, уравнения другие. Точнее, уравнение неразрывности другое. Ну и уравнение состояния тоже своё
alexhott
28.03.2017 20:13а волны в сверхтекучей жидкости распространяются? Пловец будет генерировать волны, а это энергия кудато уходящая, и соответсвенно откудато берется. может и двигать тело в жидкости.

PhysRevB
28.03.2017 20:50+1Волны да, распространяются, но только для их возбуждения в сверхтекучей жидкости нужно двигаться со скоростью, превышающей некоторый порог (в жидком гелии это сотни метров в секунду). Этот случай как раз рассмотрен на 5-й по счету картинке.

VIK52
28.03.2017 23:30А что, при дозвуковых движениях "возбудителя" волны разве не излучаются? Просто интенсивность будет меньше, поскольку давление почти успевает выравниваться

PhysRevB
29.03.2017 10:10Вообще, критерий сверхтекучести Ландау запрещает формирование возбуждений (и, соответственно, передачу сверхтекучей жидкости импульса и энергии), если скорость движения тела меньше критической. Поэтому тело, движущееся или колеблющееся с достаточно малой скоростью, не будет создавать звуковых. Конечно, это не отменяет того, что оно будет толкать и возмущать вокруг себя жидкость, но все это будет происходить, если переходить на язык оптики, в области ближнего поля, а в дальнем поле звуковых волн не будет.

arheops
29.03.2017 04:24Ну человек плыть таки может. Вытягивая руку вдоль, вы перед собой толкаете меньше газа, чем отталкивает назад рукой. Чисто масса выкинутая назад больше. Аналогично человек плывет на станции в микрогравитации, в воздухе.
Хотя скорость без ласт на руки будет минимальна.
Расмотренные уравнения работают только для симетричных во времени движений, а у вас будет круговое, несимметричное.

Fenyx_dml
29.03.2017 19:33-2Остается только удивляться какой чушью занимаются ученые и как далеки их теоретические изыскания от реальности. При чем тут гребешки? Они что, из-за теоремы этого Порсела разучились плавать? И при чем здесь сверхзвуковое движение в жидкости (попробуйте-ка изобразить!)? Гребешки двигаются за счет реактивного момента при быстром схлопывании створок. При раскрытии скорость меньше — это во первых, а во вторых, это не полный аналог. Хоть это движение и можно прокручивать вперед-назад,, но вот жидкость-то ведет себя совершенно по разному! При всасывании нет такого сильного момента, как при выбрасывании и дело тут совсем не в вязкости. Вообще, любой пловец делает не просто движения вперед-назад, траектория движений гораздо сложнее. Это надо совершенно не уметь плавать, чтобы этого не понимать. Как и то, что если находясь в воде просто махать руками вперед-назад, то поплывешь только в одну сторону — на дно!
Если же не начинать от таких неуместных аналогий, как это сделано в статье, а непосредственно с поставленной задачи, то аналогию можно было взять у кольчатых червей и змей. Если представить себе три шара, соединенных «змейкой», то периодические волнообразные изменения размеров шаров (увеличение переднего шара, затем среднего, затем заднего и по кругу) или извивания — очевидные способы перемещения. Дальше уже можно математический аппарат подводить.
PhysRevB
29.03.2017 23:48+2Движение морского гребешка возможно только при некоторых промежуточных значениях числа Рейнольдса.
Если число Рейнольдса очень малое (это случай предельно вязкой жидкости, очень малых размеров, как для микроорганизмов или очень малой скорости движения), то работает теорема Пёрселла, и такой способ движения не годится. Просто не будет реактивной струи. Соответственно, микроорганизмы его использовать не могут, а используют извивания или жгутики.
Если же число Рейнольдса очень большое (это случай сверхтекучей жидкости), то работает аналог теоремы Пёрселла, и способ передвижения морского гребешка тоже не работает.
Как раз в этой статье (и в других цитированных в ней статьях) и подводится строгий математический аппарат под все эти вещи.Vjatcheslav3345
30.03.2017 13:07Многие водные микроорганизмы миллиарды лет имеют кремниевый панцирь, но никто не передвигается хлопая его створками — как моллюск.

Fenyx_dml
30.03.2017 22:47Спасибо за разъяснения, но в статье я никаким образом этого не увидел. Там упоминается гребешок, сразу же скачок к некоему «пловцу» из двух частей, который с гребешком ничего общего не имеет.


Flagman
Спасибо за статью! Очень пригодится, если придётся плыть в сверхтекучей жидкости (например, в жидком гелии).
eugenius_nsk
«Сами топите урановые ломы в ртути!» (с)
wwarlock
Придёт время, научимся загружать своё сознание в механические тела, выдерживающие критические условия, нам и не такие навыки пригодятся.
Впрочем, есть еще другие планеты/спутники, где вопросы проходимости дронов, стоят очень остро уже прямо сейчас.