Да, дорогой читатель, такое тоже бывает, и может быть вкусно и полезно!
Как ты уже наверняка знаешь, дорогой читатель, существует два способа построения цифровых фильтров. Это рекурсивные фильтры, они же фильтры с бесконечной импульсной характеристикой (БИХ), и трансверсальные фильтры, они же фильтры с конечной импульсной характеристикой (КИХ). Самым простым и широко используемым фильтром КИХ является «фильтр скользящего среднего». Результат фильтрации такого фильтра, есть среднее арифметическое последних N отсчетов входного сигнала.
Или, в развернутом виде, для N=4:
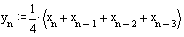
Функция на языке С реализующая фильтр скользящего среднего:
#define N (4)
int filter(int a)
{
static int m[N];
static int n;
m[n]=a;
n=(n+1)%N;
a=0;
for(int j=0;j<N;j++){a=a+m[j];}
return a/N;
}
Комплексный коэффициент передачи фильтра скользящего среднего, нормированный относительно частоты дискретизации, определится как преобразование Фурье от импульсной характеристики:
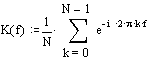
График амплитудно-частотной характеристики (АЧХ), нормированной относительно частоты дискретизации, при различных значениях длинны фильтра (N=4;8;16), приведен на рисунке:
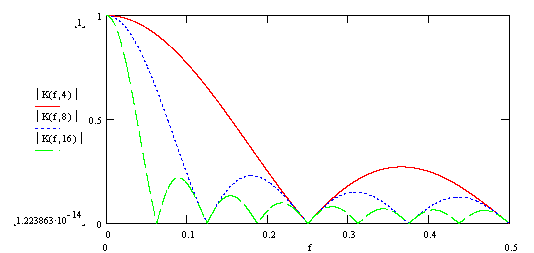
Соответственно, график фазо-частотной характеристики (ФЧХ):
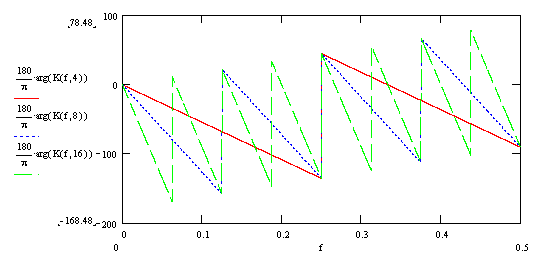
Данный фильтр нашел широкое применение в обработке сигналов, отчасти благодаря своей простоте, но самое главное его свойство — линейная фазо-частотная характеристика, и, соответственно, постоянное во всей полосе частот время запаздывания сигнала. Этот фильтр трансформирует амплитудный спектр сигнала, не затрагивая фазовый, что делает удобным его использование в системах регулирования. Фильтр скользящего среднего, благодаря своей линейной переходной характеристике, широко применяется при линейной интерполяции, передискретизации сигнала и т.п.
Главный недостаток фильтра скользящего среднего — вычислительная сложность, пропорциональная длине фильтра N. Для решения этой проблемы существует рекурсивный фильтр скользящего среднего. То есть, фильтр, имеющий те же характеристики, что и классический фильтр скользящего среднего, но реализованный по рекурсивной схеме. Такие типы фильтров широко известны в узких кругах, и называются: рекурсивные фильтры с линейной ФЧХ [Введение в цифровую фильтрацию. Под. ред. Богнера Р. М: 1976] или CIC-фильтры [DspLib]. Существует научная школа проф. Турулина И.И. [РГБ], занимающаяся исследованием подобных фильтров.
Покажем способ построения рекурсивного фильтра скользящего среднего на примере фильтра длинной N=4. Впоследствии нетрудно будет обобщить результаты на произвольную длину фильтра.
Как было отмечено выше, значение n-ного отсчета сигнала на выходе фильтра можно определить как:
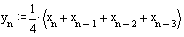
А значение предыдущего, ((n-1)-го) отсчета:
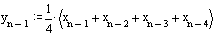
Вычтем из первого выражения второе, в результате получим:
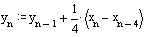
Нетрудно сообразить, что при произвольной длине фильтра N, уравнение запишется в следующем виде:
(1)На основании приведенного уравнения можно записать код фильтра на языке С, но сначала мы выполним проверку наших выкладок. Найдем частотные характеристики рекурсивного фильтра скользящего среднего, для чего выполним Z-преобразование уравнения фильтра. Хочу напомнить дорогому читателю, что для выполнения Z-преобразования необходимо заменить переменные (xn,yn) их Z-отображениями (X,Y), каждое понижение индекса переменной на единицу соответствует умножению Z-1.
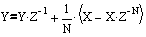
Решим полученное уравнение относительно Y/X –коэффициента передачи фильтра
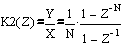
Перейдем из Z-области в частотную область, заменив
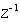на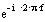 
, и получим комплексный коэффициент передачи: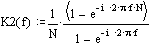
Построим график модуля комплексного коэффициента передачи (АЧХ фильтра), при различных значениях N=4,8,16:
А также аргумент комплексного коэффициента передачи (ФЧХ фильтра):
Как видно из приведенных графиков, частотные характеристики классического фильтра скользящего среднего и рекурсивного фильтра скользящего среднего полностью совпадают.
Перейдем к реализации фильтра. При непосредственной реализации по уравнению фильтра (1) в условиях целочисленной арифметики возможны некоторые трудности. При выполнении операции деления на N в целочисленной арифметике возникает потеря значащих разрядов, что приводит к нелинейным искажениям сигнала на выходе фильтра. Для разрешения этих трудностей необходимо исключить операцию деления из рекуррентного уравнения фильтра. Для чего умножим обе части уравнения фильтра (1) на N.
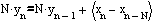
В полученном выражении выполним подстановку:
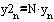
В результате уравнение фильтра (1) преобразуется в систему уравнений:
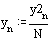
На основании системы уравнений фильтра запишем код, реализующий фильтр на языке С.
#define N (4)
int filter(int x)
{
static int n;
static int m[N];
static int y;
y=y+(x-m[n]);
m[n]=x;
n=(n+1)%N;
return y/N;
}Стоит отметить, что любители «совершенного кода» могут наложить ограничивающие требования на длину фильтра N. При длине фильтра, равной степеням двойки (2,4,8,16…), можно заменить операцию деления (/) арифметическим сдвигом (>>), операцию остаток от деления (%) — побитовой конъюнкцией (&).
Заключение
Дорогой читатель, целью данной публикации не столько познакомить тебя с рекурсивным фильтром скользящего среднего, очень может быть, что ты про него прекрасно знаешь. Цель данной публикации познакомить тебя, дорогой читатель, с некоторыми практическими приемами анализа и синтеза цифровых фильтров. Посмотри, как просто мы перешли от трансверсального фильтра к рекурсивному, и Z-преобразование не так страшно, как его малюют. Надеюсь также, что метод повышения точности вычисления рекуррентных выражений в условиях целочисленной арифметики будет полезен тебе.
Успехов тебе, дорогой читатель!
Комментарии (44)
aamonster
04.04.2017 09:48"Главный недостаток фильтра скользящего среднего — вычислительная сложность, пропорциональная длине фильтра N." — ну надо ж было ляпнуть такую ерунду. Вычислительная сложность — одно сложение, одно вычитание, одно деление на константу (заменяется на умножение, а то и на сдвиг). O(1).
Вот памяти O(N) надо, это да. Поэтому на совсем мелких девайсах непопулярен. И других недостатков хватает.
arteast
04.04.2017 10:00+1Автор имел в виду нерекурсивный фильтр (т.е. функция от предыдущих N входных отсчетов) — а он реализуется как сумматор-делитель всех отсчетов, со сложностью O(N).
Indemsys
04.04.2017 10:06Сложить, вычесть — это и есть «открытый» автором рекурсивный фильтр.
А изначальный фильтр у него — все сложить.
Причем у автора в программе ошибка.
aamonster
04.04.2017 11:00+2В следующей статье автор расскажет, как можно 2+2+2+2+2 заменить на 2*5?
При этом приведя кучу формул и наукообразной терминологии?
Tsvetik
04.04.2017 12:27Чем же рекурсивный вариант лучше прямого? Все равно N значений в памяти хранить
IBAH_II
04.04.2017 12:32но вычислять то одно
FGV
04.04.2017 14:18тогда зачем хранить n отсчетов?
FGV
04.04.2017 14:50Нда, без буффера никак, по сути надо реализовывать задержку в N отсчетов. Чего кстати в последней реализации на си не видно, думаю так будет корректнее:
#define N (4)
int filter(int x)
{
static int m[N];
static int y;
y=y+(x-m[0]);
for (int i=1;i<N;i++) m[i-1]=m[i];
m[N-1]=x;
return y/N;
}
Alexeyslav
04.04.2017 15:34+1Ужасно-ужасно! Двигать массив поэлементно? Это будет дольше чем считать «по полной программе».
Вместо того чтобы двигать «окно» лучше организовать классический кольцевой буфер — двигается указатель, а массив остаётся на месте. Число по указателю извлекаем — это будет последний элемент буфера, новое на его место записываем — это будет начало буфера, и сдвигаем указатель по кругу на 1 позицию. Никаких перекидываний целых кусков памяти!
Представьте себе крайнюю ситуацию, когда N = 2000000 и каждую итерацию вам надо будет 2млн элементов сдвинуть на одну позицию… да быстрее их будет сложить и не парится с рекурсивным вычислением.
IBAH_II
04.04.2017 19:34оно може и понятнее, но работает дольше
«Чего кстати в последней реализации на си не видно»
по моему отлично видно «n=(n+1)%N;»
я так понимаю большинство собравшихся тупит по патерну КИХ фильтра
Поясню. Входные данные складываются в буфер, указатель буфера закольцовывается n=(n+1)%N;
Значение указателя и есть нулевой отсчет, или согласно математическим формулам n-ный отсчет
Минус первый (n-1) отсчет это (n+N-1)%N, или в условиях N=2^L (n-1)&(N-1)
Минус k-тый (n-k) это (n+N-k)%N при условии что k<N, отсчеты k>N не сохранены
Alexeyslav
04.04.2017 13:35Прямой — надо складывать все N значений, потом делить…
А рекурсивный — сложить текущее значение(начало окна) и вычесть последнее(конец окна), и одно деление.erwins22
04.04.2017 13:45Вероятно этот алгоритм медленнее так как предусматривает дополнительную запись в память.
Думаю сложение 4х будет быстрееAlexeyslav
04.04.2017 14:07Это какую дополнительную? Обычно в таких алгоритмах используют кольцевой буфер — по указателю считали ячейку и это будет наш последний элемент, и на его место вписали свежее значение, передвинули указатель на следующий элемент или перешли на начало если это конец выделенной области под массив.
esaulenka
04.04.2017 16:42Во-первых, тут ОДНА дополнительная запись. В нерекурсивном оригинале будет 4 (а в большинстве случаев куда больше, скажем 64) чтения из той же памяти.
А во-вторых, это микроконтроллер. Если ОЗУ набортная (есть «толстые» модели с внешней памятью, но во всяких DIY это редкость), доступ к ней — ровно один такт.erwins22
04.04.2017 18:59Заметьте, ОДНА дополнительная ЗАПИСЬ.
Так как есть требование когерентности кеша то данная операция отразиться на замедлении всех ядер.
Сейчас основные тормоза это совсем не сложение или умножение — это чтение и запись в память.
доступ к памяти десятки и сотни тактов.
Deosis
05.04.2017 06:51Когерентность кэша нужна, если один фильтр считается из разных потоков. Так сделать можно, но зачем?
ПС. Если считать строго, то записей в память больше:
не рекурсивный) чтение и запись индекса, запись в массив, N ЧТЕНИЙ из массива
рекурсивный) чтение и запись индекса, ЧТЕНИЕ и запись в массив, ЧТЕНИЕ и ЗАПИСЬ суммы.
В первом случае мы задействуем N+1 адрес памяти за раз, во втором 3
Чем больше N тем больше промахов кэша будет в первом случае. Во втором количество промахов почти не зависит от N.
ilynxy
04.04.2017 21:03А как же CIC фильтр и Hogenauer pruning для пущей экономии?
IBAH_II
05.04.2017 09:42так этож оно и есть
Такие типы фильтров широко известны в узких кругах, и называются: рекурсивные фильтры с линейной ФЧХ [Введение в цифровую фильтрацию. Под. ред. Богнера Р. М: 1976] или CIC-фильтры [DspLib]. Существует научная школа проф. Турулина И.И. [РГБ], занимающаяся исследованием подобных фильтров.
Refridgerator
05.04.2017 07:03+1Ещё такой фильтр неустойчивый — при реализации на числах с плавающей точкой он через некоторое время станет накапливать постоянную составляющую.
Alexeyslav
Ещё одна очевидная проблема рекурсивного фильтра — малейшее однократное повреждение данных приводит к перманентному искажению результата, а оно в реальных системах может произойти по разным причинам — космическое излучение, несанкционированная запись в область памяти массива со значениями и т.д. поэтому для надёжности иногда приходится пересчитывать по полной весь массив. Или должна быть какая-то обратная связь которая устранит расхождение.
IBAH_II
Селяви, как говорят французы
Tsvetik
В рекурсивном варианте некоторое отклоение d на шаге k даст вклад в выход фильтра +d/N, но потом на шаге k+N это же отклонение вычтется.
Alexeyslav
Если значение в массиве изменится несанкционировано, то вычтется уже совсем другая величина…
knstqq
(удалено, дубликат)
esaulenka
В системах, у которых есть эти самые «малейшие однократные повреждения данных», проблем куда больше.
Потому что вероятность, что слетит стек, какой-нибудь индекс или прочий указатель ровно такая же.
Нет, я знаю про ватчдог, но это есть костыль — система перед его срабатыванием имела полное право делать чёрт-знает-что.
Tsvetik
А какие еще есть костыли для систем с возможным повреждениями данных?
Из программных средств для контроля целостности стека вызовов можно каждой функции передавать параметр CalledById и внутри функции его проверять. Желательно иметь поддержку такой фичи на уровне компилятора.
esaulenka
Вариант, в котором можно быть уверенным — дублировать (троировать) системы управления.
А «иногда пересчитывать» этот несчастный фильтр — это из анекдота о поиске кошелька под фонарём.
Alexeyslav
Троирование системы управления не поможет, т.к. программа на них будет одна и программная ошибка сделает плохо на всех экземплярах. Она в любом случае сделает плохо, даже если всё работать будет идеально — как только используешь арифметику с плавающей запятой — будет накапливаться неустранимая ошибка из-за неизбежного округления.
esaulenka
У меня тут вопрос возник. У Вас какая проблема?
Космические излучения? Дублируйте. Иначе за то время, что пройдёт между прилётом частицы и очередным пересчётом фильтра Ваш космолёт включит самый-главный-двигатель и улетит чёрт знает куда.
Программные ошибки? Пересчитывать каждые 5 секунд одни и те же данные с одной и той же ошибкой… Не лучшее решение.
Накопление ошибки во флоатах? Всё просто — не делайте так никогда. Разговор не с этого начался.
Или просто поговорить надо на отвлечённые темы?.. Тогда, пожалуйста, не ко мне.
Alexeyslav
Дело в том что однократная ошибка в случае полного пересчета уйдёт со временем и больше беспокоить не будет, а для рекурсивного алгоритма ошибка засядет надолго и если это девайс с аптаймом в 15 лет, за такой срок ошибок накопится просто вагон. А если его перезапускать каждые сутки никто ничего не заметит, конечно. Вот для этого и нужны пересчёта по полной, чтобы периодически сбрасывать возможные ошибки и не допускать их накопления. Независимо от их природы.
Alexeyslav
По большей части, повреждения данных не приводят к перманентным искажениям данных, даже повреждение стека — поток рано или поздно будет завершен аварийно, но система продолжит работать. А тут данные, обнаружить изменение которых нет никакой возможности а последствия — перманентные искажения, на основе которых будут приниматься какие-то важные решения.
Вач-дог спасает совсем от других проблем.
Система должна обладать свойством самовосстановления после сбоя, даже если часть данных будет потеряна она должна продолжить работать.