
На некотором сайте, в некотором форуме, добрый молодец по прозвищу SciFi озадачил коллектив свой историей.
Нашел он в руководящих технических материалах иноземной фирмы Texas Instruments [FSK Modulation and Demodulation With the MSP430 Microcontroller] требуемый ему цифровой фильтр. Но иноземцы шибко хитры оказались, и в исходном коде привели следующее:
**************************************************
* Running this filter takes 113 cycles
**************************************************
;*****************************************************
; New simpler filter at following specification
; Freq_Stop: 2.5KHz, Attenuation_Stop: 40dB
; Freq_Pass: 1.4KHz, Attenuation_Pass: 1dB
; Order of filter = 5
;*****************************************************
filters:
bis #INTERRUPT_TOGGLE,global_status
mov #WDF_PARMS,mem_ptr
.word 4f16h
.word 0000h
.word 498fh
.word 0000h
.word 4f17h
.word 0008h
.word 8607h
.word 4708h
.word 1108h
.word 4806h
.word 1108h
.word 1108h
.word 1108h
.word 1108h
.word 1108h
.
.
.
Зашифровали демоны! Но добрый молодец SciFi, тоже не промах оказался. Одолел их хитрости и перевел их тайнопись на язык С:
signed short filter(signed short x)
{
static signed short fltmem[5];
signed short r6, r7, r9;
r7 = fltmem[4] - fltmem[0];
fltmem[0] = x;
r6 = (r7 >> 1) - (r7 >> 6) - fltmem[4];
fltmem[4] = fltmem[3];
fltmem[3] = r6;
r6 -= r7;
r7 = fltmem[2] - x;
r9 = (r7 >> 3) - (r7 >> 6) + fltmem[2];
r7 -= r9;
fltmem[2] = fltmem[1];
fltmem[1] = r7;
return (r6 - r9)>>1;
}
Как выяснилось, демоны шифровались дважды. Данный код получен явно с использованием компилятора, так использовать относительную адресацию может только компилятор. Но сам по себе код заслуживает интереса и уважения. Как видно, он не содержит операций умножения и может эффективно выполнятся даже на самых простых процессорах. У доброго молодца SciFi, и у всех остальных, возник вопрос: “Что это за фильтр?”.
Восстановить структурную схему фильтра по такому коду, если и возможно, то весьма трудоемко. Поэтому мы пойдем другим путем. Вывод о типе и параметрах фильтра будем делать по амплитудно-частотной характеристике (АЧХ). Как ее получить? Да как два байта переслать.
Сразу отметим, что данный фильтр является фильтром с бесконечной импульсной характеристикой. Это угадывается в исходном коде, состояние фильтра хранится в массиве static signed short fltmem[5];
Снимем 60 отсчетов импульсной характеристики фильтра, то есть, реакцию фильтра на единичный импульс. Но в условиях целочисленной арифметики, чтобы получить конечный результат с наилучшей точностью, будем подавать на вход фильтра значение не 1, а 10000. Точнее, надо подавать максимально возможное число, не вызывающие переполнения.
Тестовый код для снятия импульсной характеристики:
printf("%d\r\n", filter(10000));
for(int i=1;i<100;i++)
{
printf("%d\r\n", filter(0));
}Полученный результат, с помощью копипастинга, обработаем в математическом пакете MathCad.
Построим график импульсной характеристики. На интервале 0-20 отсчетов он выглядит так:

И на интервале 20-60 отсчетов он выглядит так:
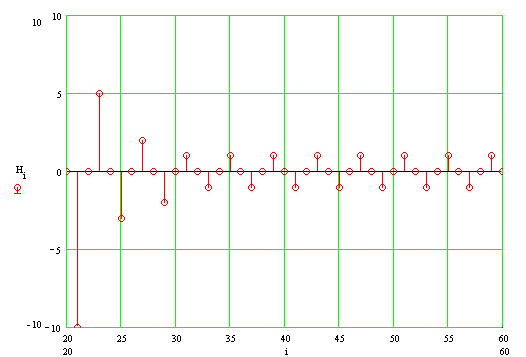
Из анализа импульсной характеристики видно, что фильтр не лишен недостатков. Импульсная характеристика содержит незатухающие колебания, амплитудой одна дискрета. В теории синтеза фильтров с бесконечной характеристикой [Гольденберг Л. М. и др. Цифровая обработка сигналов. М.: Радио и связь, 1985] такие колебания принято называть предельными циклами, которые возникают из-за ошибки округления целых чисел.
Комплексный коэффициент передачи исследуемого фильтра можно определить как преобразование Фурье от импульсной характеристики. Только в случае дискретной импульсной характеристики интегрирование по временой оси можно заменить сложением по всем ненулевым отсчетам. В нашем случае коомплексный коэффициент передачи случае определится выражением:
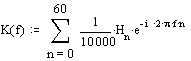
Где H – массив отсчетов импульсной характеристики;
f – частота, нормированная относительно частоты дискретизации;
Построим график модуля комплексного коэффициента передачи, амплидудно-частотную характеристику, в логарифмическом масштабе (ЛАЧХ). Здесь и далее, при построении графиков, используется частота, нормированная относительно частоты дискретизации.
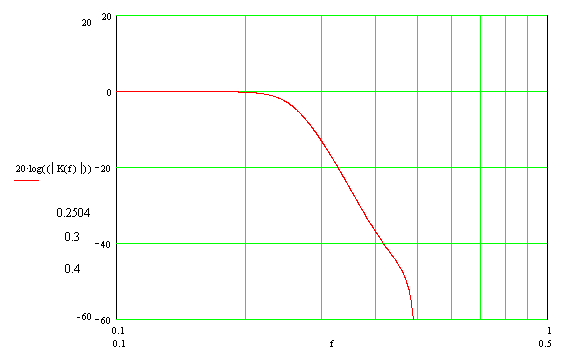
С помощью встроенных средств математического пакета определим ключевые точки АЧХ:
- Частота среза фильтра по уровню -3дБ – 0.25
- Коэффициент передачи на частоте 0.3 — -13.266дБ
- Коэффициент передачи на частоте 0.4 — -37.013дБ
Соответственно, наклон характеристики вне полосы пропускания составляет:
 Дб/декада
Дб/декадаДля полноты картины приведем фазо-частотную характеристику (ФЧХ):

Фазовый сдвиг на частоте 0.48 составляет (180+180+87)=447 градусов. Разрыв фазы на графике может вызвать недоумение, если забыть о неоднозначности арктангенса.
Так же, для полноты картины, приведем групповое время запаздывания (ГВЗ).

Теперь, глубоко задумавшись, можно ответить на вопрос “Что это за фильтр?”.
Порядок фильтра. Из анализа логарифмической амплитудно-частотной характеристики можно предположить, что данный фильтр является звеном 10 порядка, наклон характеристики вне полосы пропускания составляет около 20*10=200 дБ/декаду. Но из анализа фазовой характеристики видно, что фазовый сдвиг стремится к 90*5=450 градусам. Тут у неискушенного “угадывателя фильтров” невольно возникают мысли о неминимально-фазовости данного звена. Но не стоит забывать, что “аналоговая” частота отображается в “цифровую” через тангенс и, следовательно, законы аналогового мира (20дБ/декаду и т.п.) работают только на частотах много меньше частоты дискретизации. В нашем же случае, мы рассматриваем ЛАЧХ на участке близком к половине частоты дискретизации, и законы аналогового мира не работают.
Таким образом, по виду фазовой характеристики можно сделать вывод, что данное звено является звеном 5 порядка.
Тип фильтра. Принимая во внимания вид ЛАЧХ (в полосе пропускания ЛАЧХ максимально плоская) и вид графика ГВЗ (экстремум в окрестности частоты среза) можно предположить, что данное звено является фильтром Баттерворта. Для подтверждения нашего предположения построим ЛАЧХ, ФЧХ и ГВЗ идеального цифрового фильтра Баттерворта с частотой среза 0.25 синтезированного методом билинейного преобразования [Википедия].
На графиках красной сплошной линией обозначены величины соответствующие исследуемому фильтру, синей пунктирной линией — идеальному цифровому фильтру Баттерворта синтезированного методом билинейного преобразования



Как видно из графиков, практически полное совпадение параметров исследуемого фильтра с параметрами идеального цифрового фильтра Баттерворта синтезированного методом билинейного преобразования.
Заключение.
В данной работе мы исследовали замечательную реализацию цифрового фильтра Баттерворта 5-порядка. Данная реализация фильтра, не смотря на свои недостатки в виде предельного цикла, заслуживает большого уважения. Инженерам фирмы Texas Instruments удалось воплотить достаточно сложный алгоритм фильтра 5 порядка в целых числах, не используя операций умножения и деления, при этом обеспечить приемлемую устойчивость и соответствие характеристик фильтра прототипу.
Ваш покорный слуга, искренне надеется, что использованный в данной работе метод анализа кода цифровых фильтров будет интересен и полезен читателю.
Комментарии (36)

beeruser
22.03.2017 00:58+2«иноземной фирмы Texis Instrument»
Texas Instruments
«не используя операций умножения и деления»
(r7 >> 1) — (r7 >> 6)
r7/2 — r7/64 = r7/2.065

gunya
22.03.2017 02:57+10Битовый сдвиг != умножение. В случае, если нет математического сопроцессора, умножение может занимать далеко за десяток тактов. Битовый сдвиг всегда выполняется за один такт. Опять же, в кремнии/FPGA реализация битового сдвига делается абсолютно элементарно, в отличие от умножения.

beeruser
22.03.2017 04:52-8>> Битовый сдвиг != умножение.
Приведённый отрывок это программная реализация умножения (или деления — как угодно) с фиксированной точкой на конкретную константу.
Умножение не перестаёт быть умножением считаете вы его в столбик или на калькуляторе.
Refridgerator
22.03.2017 07:49Это если только рассматривать умножение как самоцель и результат операции. Здесь же результат — не комбинация умножений и сложений, а отфильтрованный сигнал.

beeruser
23.03.2017 18:35Ну тогда и не стоило заострять на этом внимание и нужно было рассматривать машинный код как блэк-бокс.
Но этот код дизассемблирован и сконвертирован на C с целью _изучить его работу_.
Моё естественное желание _обьяснить_ детали реализации натолкнулость на непонятное сопротивление.
Видимо, согласно первому комменту, людям проще поверить в магию, чем в возможность реализации умножения через сложение/сдвиг.

beeruser
22.03.2017 16:51-1Я смотрю тут многим не знаком алгоритм побитового умножения через сдвиг/сложение AKA умножение в столбик =)
http://users.utcluj.ro/~baruch/book_ssce/SSCE-Shift-Mult.pdf

gunya
22.03.2017 18:59+1Именно потому, что мне этот алгоритм знаком, я и говорю, что умножение в разы более затратная операция.
Посмотрите сами, для реализации битового сдвига нам понадобится:
— Сдвиговый регистр
— 1 такт на сдвиг
Если есть возможность скоммутировать выходы регистра — достаточно обычного регистра.
Для реализации умножения нам понадобится:
— Два сдвиговых регистра
— Регистр под результат
— Сумматор
— 4 такта на умножение
Про то, что комбинационная схема сумматора будет в разы медленнее, чем сдвиговый регистр, я даже говорить не буду.
beeruser
23.03.2017 18:22+1>> умножение в разы более затратная операция.
А кто-то спорит?
Я лишь показал как именно осуществляется умножение/деление, для тех кому интересно.
Причём тут ваш комментарий про «затратность»? Где-то в моём комментарии утверждалось иное?
Я говорил что мною приведённый кусок кода это не более чем оптимизированное умножение на константу.
>> 1 такт на сдвиг
Зависит от процессора. В Pentium4 сдвиг — 4 такта.Power4/PPC970 — 2 такта.
В иных сдвиг может приводить к вызову микрокода.
Чтобы был 1 такт на сдвиг (на несколько бит) ваша схема с одним сдвиговым регистром не подходит.
А вот barrel-shifter в свою очередь это довольно массивная схема, в отличие от последовательного умножителя.
Вот тут хорошо видно, что сдвигатель больше чем _всё_ ALU и пара регистров вместе взятых.
http://daveshacks.blogspot.ru/2016/01/inside-armv1-decoding-barrel-shifter.html

qw1
23.03.2017 22:34Про то, что комбинационная схема сумматора будет в разы медленнее, чем сдвиговый регистр, я даже говорить не буду.
Не спорю, умножение в общем виде гораздо затратнее этой оптимизации.
Но, ради истины, здесь два сдвига, а между ними стоит вычитание (по сложности равно сложению).
Некорректно говорить, что тут умножение заменено одним лишь сдвигом.
Просто надо всегда понимать, что происходит. На той же современной x86 32-битное умножение быстрее работает, чем 2 сдвига и 3 сложения.
ukt
22.03.2017 22:16На это можно смотреть, как взятие только старших битов.
По аналогии считаем рубли, копейки отбрасываем.
vesper-bot
22.03.2017 09:40+1Битовый сдвиг всегда выполняется за один такт.
Помнится, некоторые варианты процессоров выполняли битовый сдвиг в цикле.

netch80
27.03.2017 14:55На современной элементной базе полноценный barrel shifter дешевле, чем раскладка сдвига на много бит в цикл по одному биту.
Хотя x86 и сейчас не гарантирует быстрое выполнение для всяких нелепостей вроде RCR на несколько бит.

FGV
22.03.2017 13:41-2Битовый сдвиг != умножение.
да ну? а помоему битовый сдвиг дает те же результаты что умножение/деление на степень двойки.
В случае, если нет математического сопроцессора, умножение может занимать далеко за десяток тактов.
Первое что приходит в голову — avr, нет сопроцессора, но есть однотактная умножалка 8*8. К слову, подкласс сигнальных процессоров (особенно древние) как правило имеет умножалку на борту но не имеет математический сопроцессор.

IBAH_II
22.03.2017 11:19Прошу прощения, Texas Instruments, поправил
Может недостаточно точно выразился… Имелась в виду операция в смысле стандарта языка «Умножение — арифметическая бинарная операция ...»
Из-за прогрессирующего многоу?ровневого абстракционизма программисты забывают что на самом деле они не «пишут программы», а отдают приказы процессору. Умение дать такой приказ, чтобы он был выполнен эффективно и в срок, и есть искусство управления. В TI есть эффективные менеджеры (без кавычек) по управлению процессорами.
jok40
22.03.2017 12:42Прошу прощения, Texas Instruments, поправил
В тексте по-прежнему написано «Texis».
IIvana
22.03.2017 04:56+4Таким образом, по виду фазовой характеристики можно сделать вывод, что данное звено является звеном 5 порядка.
А докам, значит, вы не склонны верить — мало ли что они там понапишут чтобы специально запутать:
; Freq_Stop: 2.5KHz, Attenuation_Stop: 40dB
; Freq_Pass: 1.4KHz, Attenuation_Pass: 1dB
; Order of filter = 5Ну и ради исследовательского эксперимента можно в любой тулзе по проектированию фильтров (хоть тот же filterBuilder в Матлабе, да сотни их) вбить эти характеристики и поиграться с типами, в том числе и Баттерворта.

a_tarsov
22.03.2017 08:50+3Да бросьте придраться.
Человек способны в «рукопашную» разобрать происходящие процессы, а равно как и способный доходчиво объяснить. Достоин, как минимум, уважения.
А ваш способ, больше годится для работы. Т.е. когда надо просто подобрать компоненты или в поисках проблемы, если таковая возникнет… ну и прочее.
Так, что автору спасибо. Просвещайте дальше. Может появятся ещё инженеры которые понимают, что делают, а не лепят типовые решения.

Refridgerator
22.03.2017 05:54Из анализа импульсной характеристики видно, что фильтр не лишен недостатков. Импульсная характеристика содержит незатухающие колебания, амплитудой одна дискрета.
Это не недостаток, а фича — это же БИХ. При желании, этот бесконечный хвост можно было бы обрезать, добавив соответствующую логику.
stasemv
22.03.2017 08:51"Недостатки" скорее всего вызваны округлением коэффициентов фильтра до 2^(-n), чтобы стало возможным отказаться от использования умножения и деления, и заменить их на операции сдвига.

IBAH_II
22.03.2017 11:27Скорее дело не в округлении, а в фичах битовой арифметики. (-1) сколько не сдвигай влево, она так и останется (-1).
ProLimit
22.03.2017 11:45Ну да, БИХ разные бывают, но тут он должен затухать в ноль, если бы считался с бОльшей точностью. Но из-за оптимизаций вычислания, есть такой хвостик, но его посчитали допустимым (на три порядка ниже основного сигнала)

maybe_im_a_leo
22.03.2017 06:55Взял на заметку, заюзаю при случае.
А что за форум? Английский? Ссылку не дадите — поделюсь с англоязычными коллегами
Scratch
22.03.2017 09:16Если поискать в гугле .word 4f16h SciFi, то приводит прямиком сюда http://caxapa.ru/720400.html

telhin
22.03.2017 08:51С одной стороны умные ребята работают в TI, с другой стороны достаточную документацию не пишут. Страдал в свое время работая с их ЦСП.

le1ic
22.03.2017 19:48Я работал с 54 очень много, 55 (когда только появилась) и немного с 64, 67 (кажется) сериями. Проблем с документацией не помню. Баги были, да, но они в Errata описывались, их тоже надо было внимательно читать

telhin
22.03.2017 20:08OpenMP + ndk на 6678 по отдельности работают замечательно. Вместе требуют притирки в виде правильной инициализации менеджера очереди qmss. При этом из документации есть только пример с OpenMP 1.0 и работа с семафорами. Нормальная инициализация найдена через 2 недели на полу открытом git хранилище. При этом нужно поправить немало исходников mcsdk (в гайдах написано неподходящее решение), а уж про добавление какого-нибудь srio к первым двум технологиям и говорить страшно. Про забагованность ccs и говорить не хочется, но стоит отдать должное, что компилятор и линковщик замечательно описаны в гайдах.

monah_tuk
22.03.2017 09:14Великолепно! Формулы, как обычно, вызывают печаль (у меня, так как забыты уже чуть менее, чем полностью за невостребованностью), но читал как детектив.

FGV
24.03.2017 08:52+3структурная схема фильтра из статьи:

развернутая реализация для вещественных чисел:
double filtd(double x)
{
static double fltmem[5];
double out_f = (-1.515625*fltmem[4]-1.109375*fltmem[2]+0.515625*fltmem[0]+0.109375*x)*.5;
double new_flt3 = -(fltmem[4]*0.515625+fltmem[0]*0.484375);
fltmem[4] = fltmem[3];
fltmem[3] = new_flt3;
//
double new_flt1 = -(0.109375*fltmem[2]+0.890625*x);
fltmem[2] = fltmem[1];
fltmem[1] = new_flt1;
fltmem[0] = x;
return out_f;
};

chektor
28.03.2017 18:32Больше интересует применения этого «куцего» фильтра. Наверное, есть места, где его характеристики достаточно вписываются в ТЗ.

Psychosynthesis
28.03.2017 20:00Удваиваю предыдущего оратора — как этот код применять в качестве фильтра?
Тут дана функция, ок. Допустим, у нас есть некий АЦП, на выходе имеем некий массив с отсчётами этого АЦП за определённый период времени, дальше что? Скармливать этой функции по одному значению из массива?
Простите если туплю, я пока только начинаю в цифровой обработке разбираться.

IBAH_II
29.03.2017 18:24Ну почему сразу массив? скажем так — поток данных
Вызывая данную функцию с частотой F и передавая ей в качестве аргумента входной сигнал, на выходе мы получим выходной сигнал, соответствующий реакции фильтра с указанными частотными характеристиками, частота среза по уровню 0.707 будет равняться 0,25*F
еще раз, другими словами
АЦП опрашивается с частотой 1кГц
значения АЦП скармливаюся функции фильтра
по результатам строится осциллограмма
- на вход АЦП подаем синусоиду амплитудой 1000 дискрет с частотой 100Гц, на осциллограмме имеем синусоиду амплитудой 999 дискрет
- на вход АЦП подаем синусоиду амплитудой 1000 дискрет с частотой 250Гц, на осциллограмме имеем синусоиду амплитудой 707 дискрет
- на вход АЦП подаем синусоиду амплитудой 1000 дискрет с частотой 400Гц, на осциллограмме имеем синусоиду амплитудой где-то 20 дискрет
- на вход АЦП подаем синусоиду амплитудой 1000 дискрет с частотой 900Гц, на осциллограмме имеем синусоиду амплитудой 999 дискрет, частоту 100Гц, ничего не поделаешь теорема Котельникова


Meklon
Магия))