На мой взгляд самое простое с чего нужно начинать изучать нейросети — это аппроксимация таких простых математических функций, как синус, квадратичная функция, экспонента и т.д. Согласно универсальной теореме аппроксимации — нейронная сеть с одним скрытым слоем может аппроксимировать любую непрерывную функцию многих переменных с любой точностью. Главное чтобы в этой сети было достаточное количество нейронов. И еще важно удачно подобрать начальные значения весов нейронов. Чем удачнее будут подобраны веса, тем быстрее нейронная сеть будет сходиться к исходной функции.
Исходя из этого, я решил проверить эту теорему на практике, и написал вот такую вот программу:
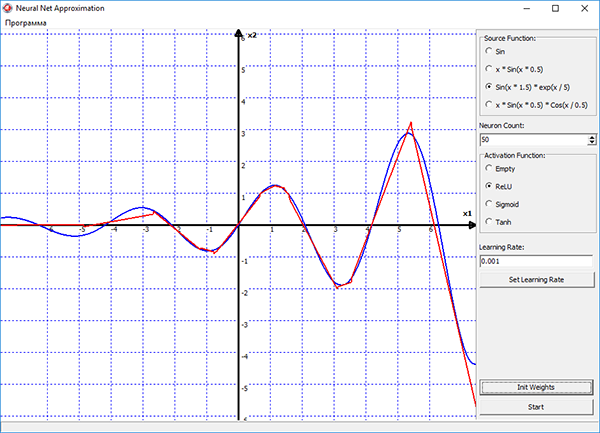
Обучение сети в программе, осуществляется методом стохастического градиентного спуска, который реализован в виде алгоритма обратного распространения ошибки. Процесс обучения наглядно отображается на графике в программе. Синим цветом на графике показана исходная функция, красным — функция построенная нейронной сетью. Можно выбирать различные функции активации для нейронов скрытого слоя, подбирать скорость обучения и изменять количество нейронов прямо в процессе обучения. И смотреть в реальном времени как изменение этих параметров влияет на процесс обучения сети.
Сама нейросеть имеет следующую структуру:
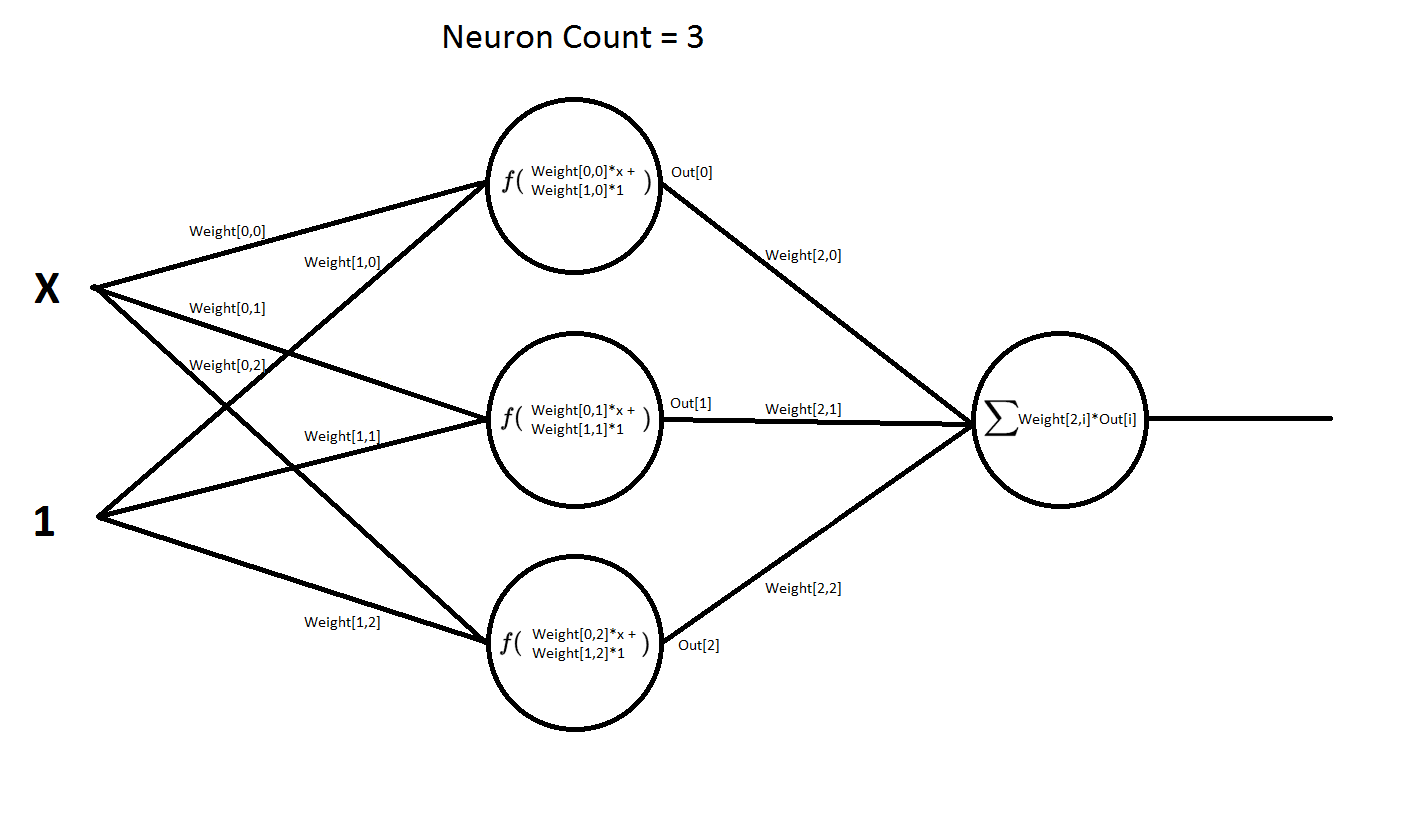
То есть она имеет два входа и один выход. Первый вход x — это значения функции, которые она может принимать по оси x. На второй вход всегда подается единица. В терминах нейросетей такой вход называется входом смещения. При его наличии сеть намного быстрее обучается и намного быстрее сходится к нужному нам результату. Эта сеть имеет два слоя слой, скрытый и выходной. На данной схеме показана сеть, которая содержит 3 нейрона в скрытом слое. Но в программе число этих нейронов можно менять в реальном времени, т.е. прямо в процессе обучения сети. Во втором же слое, число нейронов всегда неизменно. Т.е. там всегда один нейрон.
В нейронах в скрытого слоя применяется активационная функция — это может быть и выпрямитель «ReLU», сигмоид и гиперболический тангенс. Так же можно вообще убрать оттуда функцию активации «Empty», и там по сути там останется один сумматор. Будет интересно посмотреть как поведет себя сеть, не имея в себе нелинейных функций.
В нейроне второго слоя функции активации нет. Там обычный сумматор. Если бы там тоже была функция активации, то мы бы уже не смогли построить график функции нейронной сети.
Ну давайте теперь посмотрим, как это теперь всё будет работать в программе. Для начала попробуем аппроксимировать самую простою функцию синус. Поставим функцию активации на empty, то есть в нейронов скрытого слоя у нас не будет функции активации, а только сумматор. Поставим скорость обучения 00.1, Проинициализируем веса начальными случайными значениями, нажимаем кнопку старт и видим следующую картину:
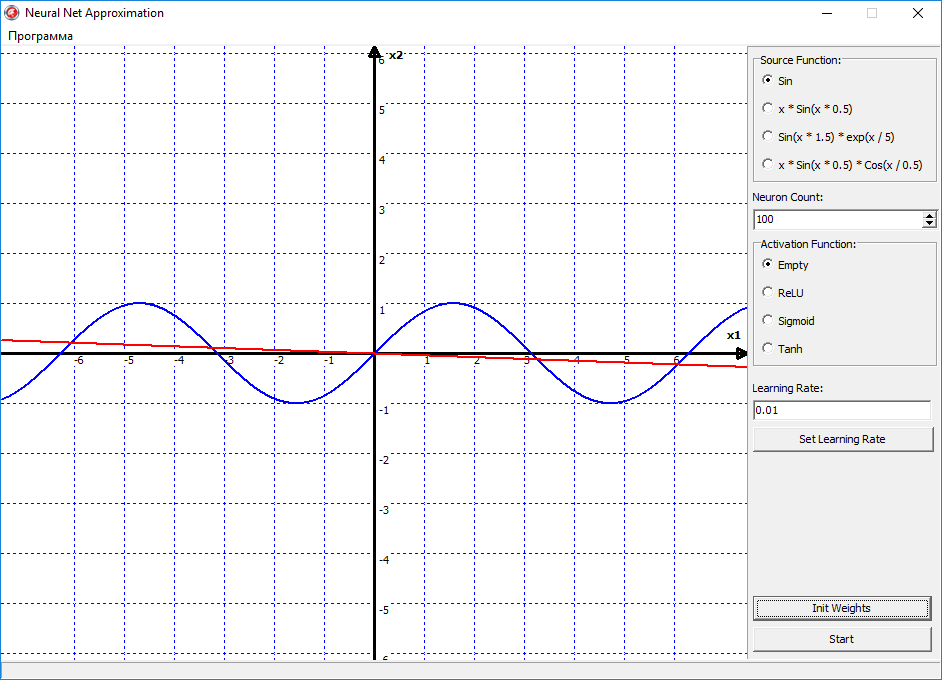
Красная линия начала дрыгаться, а это значит пошло обучение. Но теперь, как бы мы не меняли настройки программы, кол-во нейронов или скорость обучения, эта дрыгающаяся линия так и остаётся линией. Почему? Да всё очень просто. Потому что в нейронах скрытого слоя нет активационных функций, то есть нет нелинейности в нейронной сети, и на выходе она всегда будет давать прямую линию. Этот пример я показал специально, что в нейросети обязательно должна присутствовать нелинейность, иначе сеть будет выдавать всегда вот такой результат, и в итоге ничему не обучиться.
Теперь давайте попробуем переключить функцию активации на ReLU «выпрямитель», и посмотрим что будет:
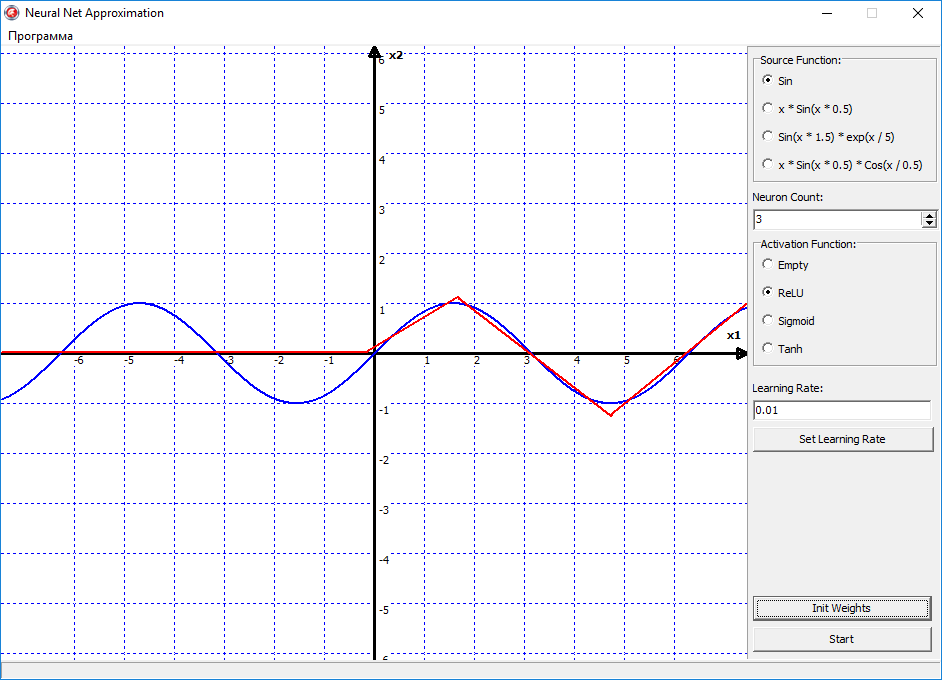
Ну вот видно, что тут уже поинтереснее начинается поведения сети, и эта линия начала выгибаться, то есть появилась нелинейность в сети. По сути, правую часть синуса, сеть уже аппроксимировала успешно. Давайте пробовать увеличивать количество нейронов, и наблюдать за изменениями:
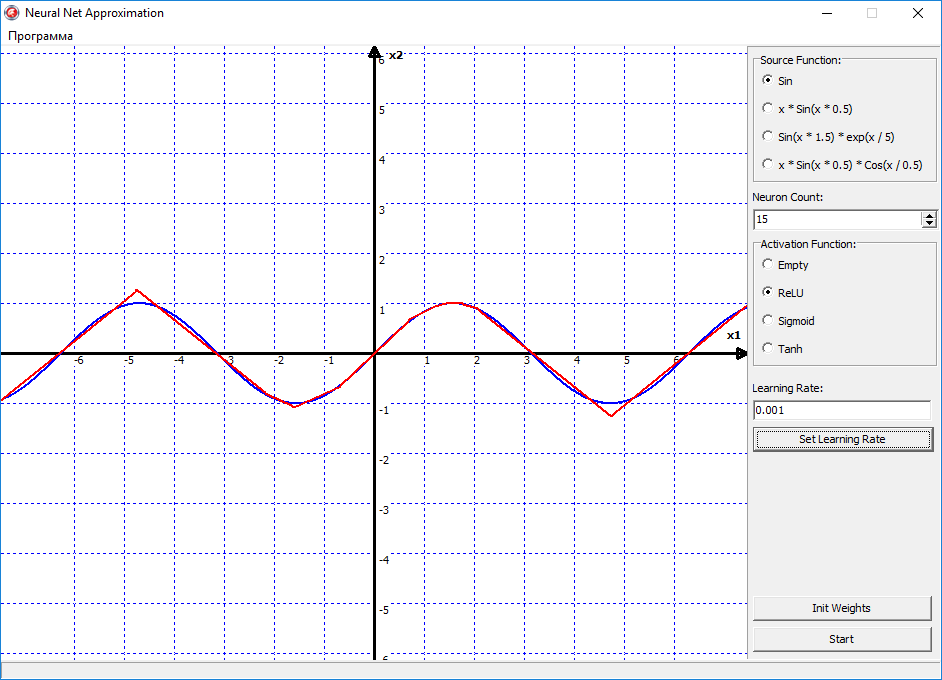
Теперь стало еще интересней, получается, что 15 нейронов в принципе хватило, чтобы более-менее аппроксимировать функцию синуса. На этом графике можно видеть, что ReLU — это всё таки грубая функция активации, то есть она ломает нашу прямую линию на множество мелких отрезков, с острыми углами. То есть если мы будем увеличивать количество нейронов, то функция будет становиться более гладкой, за счёт увеличения числа переломов, которые ломают линию на отрезки. Но преимущество ReLU в том, что это очень простая функция. И имеет очень простую производную. Соответственно скорость вычислений существенно возрастает. Поэтому ReLU можно использовать там, где не важна высокая точность, а важно скорость работы нейронной сети.
Но давайте теперь переключим функцию активации на сигмоид, и смотрим что получилось:
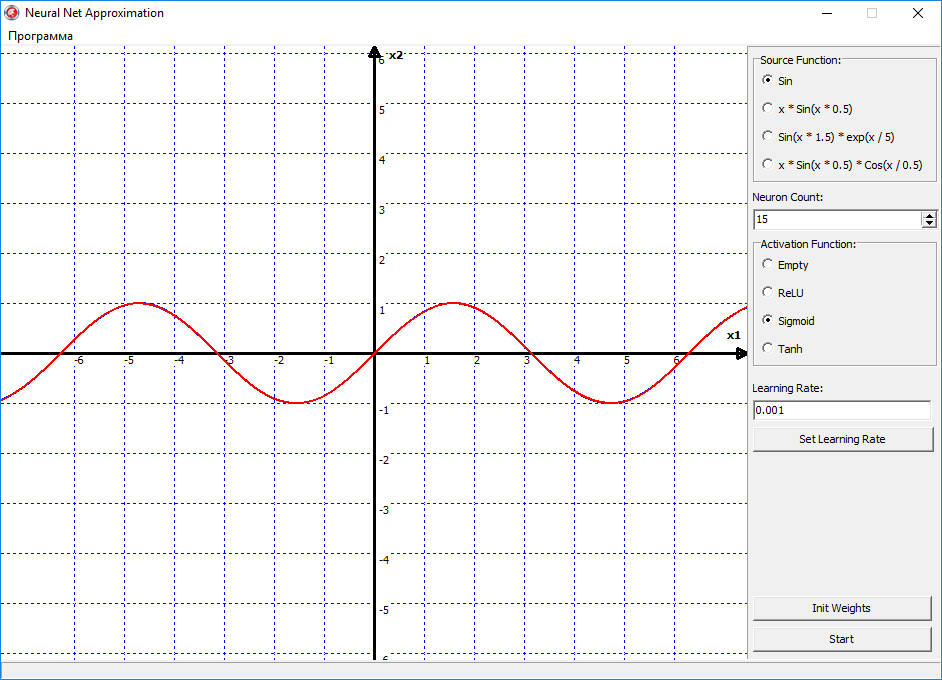
Вуаля, и сеть с идеальной точность аппроксимировала функцию синуса. Все из-за того, что сигмоид — это более гладкая функция активации. И имеет более высокую точность. В отличии от ReLU, она не ломает прямую, как если бы вы взяли в руки две соломинки, и сломали их пополам. Сигмоид же сгибает эту линию, как сгибается металлическая проволока, в отличии от хрупкой соломинки. Но конечно же недостаток сигмоида в том, что его скорость вычисления ее существенно больше.
Также если теперь переключить функцию активации на гиперболический тангенс. Сеть тоже с идеальной точностью ее аппроксимирует. Но отличие тангенса от сигмоида в том, что тангенс на выходе дает диапазон значений от -1 до 1. А сигмоид от 0 до 1. Поэтому тут уже нужно смотреть, какая функция будет лучше подходить под какую-то конкретную задачу. То есть если в вашей задачи нужно чтобы нейросеть выдавал значения от нуля до единицы, то соответственно подойдет больше сигмоид, если от минус единицы до единицы, то тангенс.
Можно также экспериментировать с аппроксимацией не только синуса, но других, совершенно различных функций. Сеть будет аппроксимировать их без проблем:
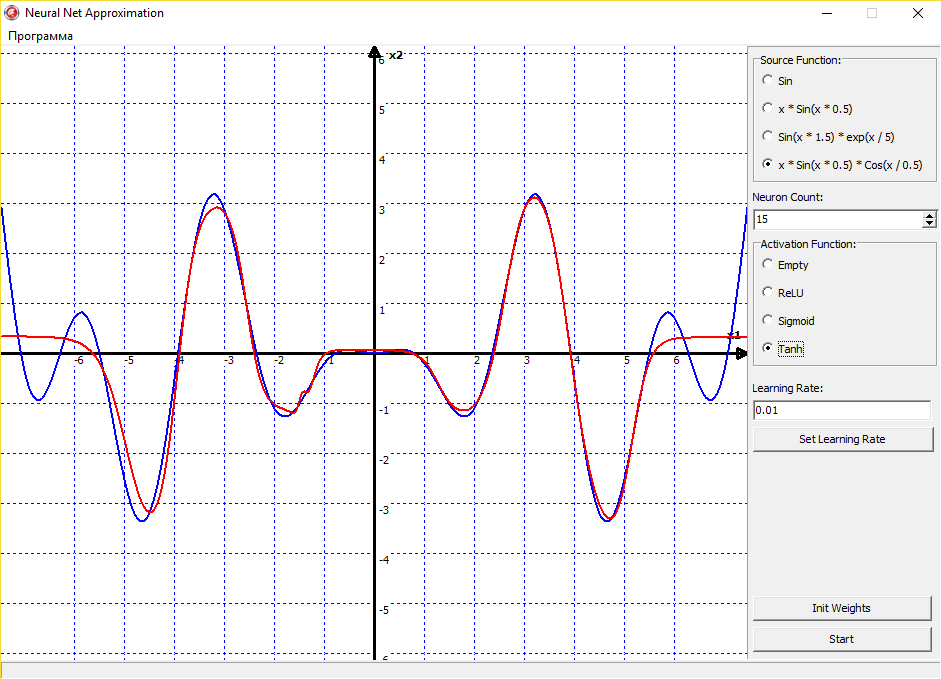
Выходит, что универсальная теорема аппроксимации действительно верна, и нейронная сеть может аппроксимировать функцию с любой точностью. Тут остается главным только правильный подбор функции активации, скорости обучения и правильная инициализация начальных значений весов. Со всем этим надо экспериментировать, нарабатывать опыт и тренировать свою интуицию. Поскольку нет какого-то четкого правила обучения нейронных сетей. Все зависит от опыта программиста, ну и еще от везения.
Комментарии (32)

kraidiky
10.07.2017 13:03Важное дополнение без которого тебя закалупают всё опытные любители нейронных сетей — скрывать от сети часть входных данных и смотреть как сеть поведёт себя на этих участках. Я бы посоветовал, например, треть входных данных на графике скрывать от обучения и отмечать эти места цветом. Потом посмотреть как качество апроксимации ведёт себя если добавить в скрытый слой больше чем надо нейронов. Бывает довольно поучительное зрелище. А у некоторых других алгоритмов и при правильной регуляризации наоборот получается всё хорошо и красиво.

MaximChistov
10.07.2017 13:16Но преимущество ReLU в том, что это очень простая функция. И имеет очень простую производную. Соответственно скорость вычислений существенно возрастает. Поэтому ReLU можно использовать там, где не важна высокая точность, а важно скорость работы нейронной сети.
Нифига подобного. Преимущество ReLU в том, что для нее не надо подгонять входные и выходные данные под диапозон [0;1] или [-1;1] с нормированием. Что в реальной жизни на реальных данных далеко не всегда возможно.(Далеко не для всех данных известны максимумы и минимумы, без чего нормализация будет неточной).
А теперь по функции. Вы решаете проблему, у которой уже есть решения намного более простые и эффективные чем нейронные сети — вывод функции по точкам 100% ей принадлежащим. Для этого нейросети не нужны! А нужны они в реальной жизни, когда к данным примешан случайный шум. И простые алгоритмы аппроксимации показывают себя намного хуже. Хотите, чтобы ваша демка была про нейросети — реализуйте добавление случайного шума хотя бы +-5% ко всем входным f(x).
Ну и, как правильно указали выше, гораздо интереснее будет выведение нейросетей для замнутых или самопересекающихся кривых, где нейросети пишутся намного быстрее и лучше аналогов.
alex_ey
10.07.2017 13:39+1Про relu, такого не знал, спасибо. Я никакую проблему не решал. Этот пример учебный, и сделал для того что бы лучше понять, как работают/обучаются нейросети. Может еще кому-нибудь этот пример и статья пригодится. Начал с самого простого, и до примерами с шумом еще доберусь.

daiver19
11.07.2017 02:05Что-то я не слышал никогда такого аргумента о ReLU. Их основное преимущество — гораздо меньше шансов на затухание и «взрыв» градиента. Собственно, использование ReLU было одним из важных шагов по построению рабочих глубоких нейросетей (ну и скорость тоже, в принципе). А вот масштабировать данные всё равно стоит в подавляющем большинстве случаев.

gudvinr
10.07.2017 13:20+2То есть, вы предлагаете скачать левый бинарник? И исходники доступны только после покупки, так что проверить и скомпилировать самостоятельно для проверки не выйдет.
Запускать исполняемые файлы из недоверенных источников любой здравомыслящий человек не будет.
В статье никакой описательной части по существу моделей, алгоритмов и принципов работы нет. Просто полотно с красивыми картинками.
Получается, вся суть в том, чтобы продать кота в мешке?
alex_ey
10.07.2017 13:46-3Ну если вы переживаете из-за вирусов в исполняемом файле, то уверяю вас, там их нет.
Ну насчет исходников, мое право делать с ними все что захочу. Тем более подчеркиваю что эта статья не рекламнаю, тут про их продажу ничего нет. Есть лишь в видео и на моем сайте.

YaakovTooth
12.07.2017 15:10С вирусами или без вирусов (сам с ними разберусь без проблем), давайте, пожалуйста, бинарник побаловаться. :)

myxo
10.07.2017 17:04+1Зачем ещё одна начальная статья по нейронным сетям?
«Выходит, что универсальная теорема аппроксимации действительно верна».
Нельзя так говорить. Вы лишь проверили пару примеров (и то, это на самом деле не проверка). Нельзя на основе этого утверждать о верности теоремы.

ImSept
10.07.2017 17:40Уважаемый автор, если вы любите сложные задачи, могу подкинуть материал для размышления из геофизической среды. Сам занимаюсь обратными задачами и пытался использовать сети, но, увы, не вышло ничего хорошего.

alex_ey
10.07.2017 17:42-1Да я только начал изучение этой темы. Сомневаюсь что у меня сразу получится решить задачу из практики, тем более такую сложную.
erwins22
10.07.2017 18:34LeakRelu
CRelu
и еще какие нить функции активации было бы интересно посмотреть

aamonster
10.07.2017 23:30троллейбус.jpg
Взять нейронную сеть и начать с её помощью решать задачу, для которой она заведомо не очень хороша? Ну… Может, как учебная задачка и сойдёт, но я бы не стал.
ilmarin77
11.07.2017 07:34+1Функцию Дирихле аппроксимируй, для интереса.

kraidiky
13.07.2017 14:57Ой, а можно я!!! Можно я!!! Моя апроксимация:
(double x) => { return 1; }
Даёт 100%-ную точность приближения, как показывают тесты.
Ну что умник, сам догадаешься почему, или подсказка через сутки? :)
ilmarin77
13.07.2017 16:46Свойства не те.

kraidiky
14.07.2017 14:59-1Иногда лучше быть добрым, чем не самым умным.
Сможешь привести пример кода, который продемонстрирует, что свойства не те?
А знаешь почему не сможешь? Потому что не целые числа в компьютере представляются в виде чисел с плавающей точкой, а они, так уж исторически сложилось, могут представлять только рациональные числа.
Будь добрее к людям, и менее язвителен.

morincer
12.07.2017 08:16Выходит, что универсальная теорема аппроксимации действительно верна
А разве ее не доказал Цыбенко еще в 1989 году?
В целом, пока пока статья смотрится бледновато — особенных глубин понимания не продемонстрировано. Настоятельно рекомендую посмотреть на курсере курс Machine Learning стэнфордского университета, хотя бы первые 4 недели курса. Там буквально на пальцах разжевывается суть задачи приближения функции и то, как она связана с нейронной сетью. В частности, там вы узнаете, почему добавление весового нейрона улучшает сходимость, в чем прелесть нормирования входных данных, и как можно строить нелинейные приближения, используя линейную функцию активации
kraidiky
12.07.2017 12:48Проблема изучения по курсам в том, что человек оказывается малоспособен воспринимать то что осталось за рамками курса. Вот точно так же начав с апроксимации, только я приближал функцию двух переменных, я получил новые знания о эфекте регуляризации на обобщающие способности сети. А те, кто учили по курсам в большинстве своём даже не способны были понять о чём идёт речь, особенно столкнувшись с хоть чуть отличающейся задачи.
ИМХО — правильный путь от половины до четверти пути, там где ты на основе подсказок и намёков понять что именно нужно делать чтобы это увидеть/провеить делать самому, потом снова читать чтобы нахвататься новых идей подсказок и готовых решений для следующей самостоятельно работы.

EndUser
16.07.2017 14:32Я не совсем понял: аппроксимация требует несколько двухмерных точек. А у вас на входе одинокое значение. Где второе для одинокой точки? Как вводятся другие точки?

alex_ey
17.07.2017 07:14Не понял вопроса. И что значит «одинокое значение»?

EndUser
17.07.2017 11:35Для аппроксимации нужна входная информация {x, f(x)}. Например, (-5, 0.96), (-4, 0.76), (-3, -0.14), (-2, -0.91), (-1, -0.84), (0, 0), (1, 0.84), (2, 0.91), (3, 0.14), (4, -0.76), (5, -0.96). Это синус. Для аппроксимации полиномом желательно иметь точек количеством не менее степени полинома, лучше больше. Если меньше, то аппроксимация станет бессмысленной, вообще не аппроксимирующей. А уж ввод функции без аргумента делает аппроксимацию просто невозможной.
В статье этот вопрос не раскрыт напрочь. То есть для любой выбранной одинокой точки в сеть скармливается только f(x), без x. И не понятно сколько раз вводится.

alex_ey
17.07.2017 12:16Ну если вы невнимательно смотрели на схему, то в сеть скармливается x, а не f(x). На выходе сеть дает значение NetOut. Вычисляется ошибка сети, error = f(x) — NetOut. В соответствии с этой ошибкой корректируется веса. Таким образом делается 10 000 итераций (эпоха обучения). После каждой эпохи, график сети обновляется в программе.



Denxc
Было бы интересно посмотреть на аппроксимацию замкнутых кривых!
alex_ey
У меня уже получилось аппроксимировать окружность, там просто в сеть добавится еще один вход y, плюс еще один скрытый слой. Позже напишу статью об этом.
BelerafonL
Есть в интрнетах готовая красивая онлайн-программка для визуализации простых нейросетей http://playground.tensorflow.org .
alex_ey
Я понимаю, что все это уже есть. Но суть в том, что когда ты напишешь свою программу с нуля, больше будешь понимать некоторые нюансы работы нейросетей. Которые можно упустить, если пользоваться уже готовыми решениями.