Введение

Приветствую, уважаемые читатели! Сегодня предлагаю поразмышлять о следующей задачке:

Дано $$ пар точек на плоскости $$. Все $$ различны. Необходимо найти многочлен $$ такой, что $$, где $$

Переводя на русский язык имеем: Иван загадал $$ точек на плоскости, а Мария, имея эту информацию, должна придумать функцию, которая (по меньшей мере) будет проходить через все эти точки. В рамках текущей статьи наша задача сводится к помощи Марии окольными путями.

«Почему окольными путями?» — спросите вы. Ответ традиционный: это статья является продолжением серии статей дилетантского характера про математику, целью которых является популяризация математического мира.

Процесс

Для начала стоит отметить, что некоторое кол-во интерполяционных многочленов уже, разумеется, существует. Оные полиномы как раз предназначены для решения искомой задачи. Среди них особенно известны такие как полином Лагранжа и Ньютона.

А также необходимо внести ясность, что такое «произвольные функции» (термин приходит из названия текущей статьи). Под ними понимается любая унарная функция, результат которой есть биективное отображение аргумента.

В рамках статьи предлагаю за такую функцию взять десятичный логарифм $$ и следующие точки:

$$

Представляя их на плоскости, должно получится нечто следующее:


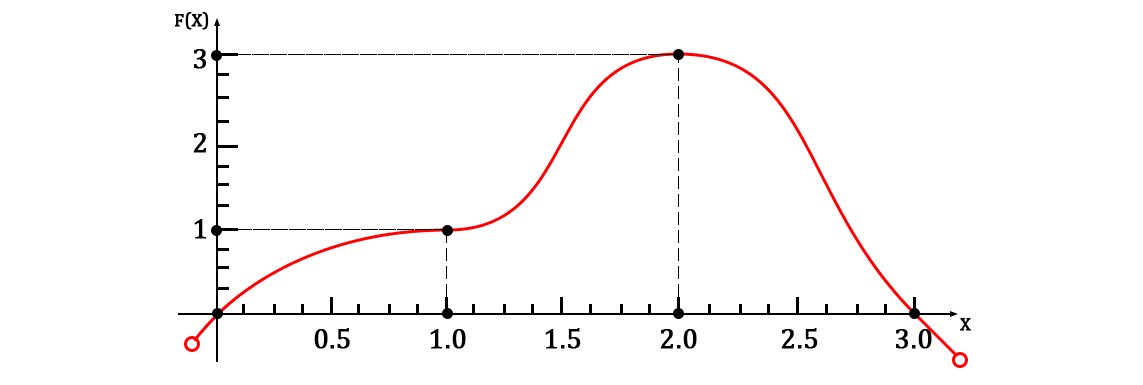
Нетрудно заметить, что сейчас кол-во пар точек равно $$.

При решении данной задачи приходит на ум некая системы уравнений, где кол-во линейно-независимых строк равно $$. Что же это за система уравнений такая?

Давайте попробуем функцию записать в виде суммы десятичных логарифмов с коэффициентами про оных (да так, чтобы кол-во коэффициентов было равно $$):

$$

Аргументы при $$ различные чтобы избежать линейной зависимости строк в будущем (можно придумать другие). А также, учитывая, что область определения функции как минимум $$ (на основе заданных условием точек), мы таким образом обеспечиваем существование области значений для функции $$ в этой области определения.

Так как нам известны $$ пар точек, то обратимся к ним для того, чтобы построить следующую тривиальную систему:

$$

Тривиальность системы заключается в том, что мы просто найдем такие $$, которые будет удовлетворять всему набору условия.

Собственно решая данную систему относительно $$ получим следующее решение:

$$

На этом задача естественным образом подходит к концу, остается только записать это в единую функцию:

$$

Она, разумеется, будет проходить через заданный набор точек. А график функции будет выглядеть следующим образом:


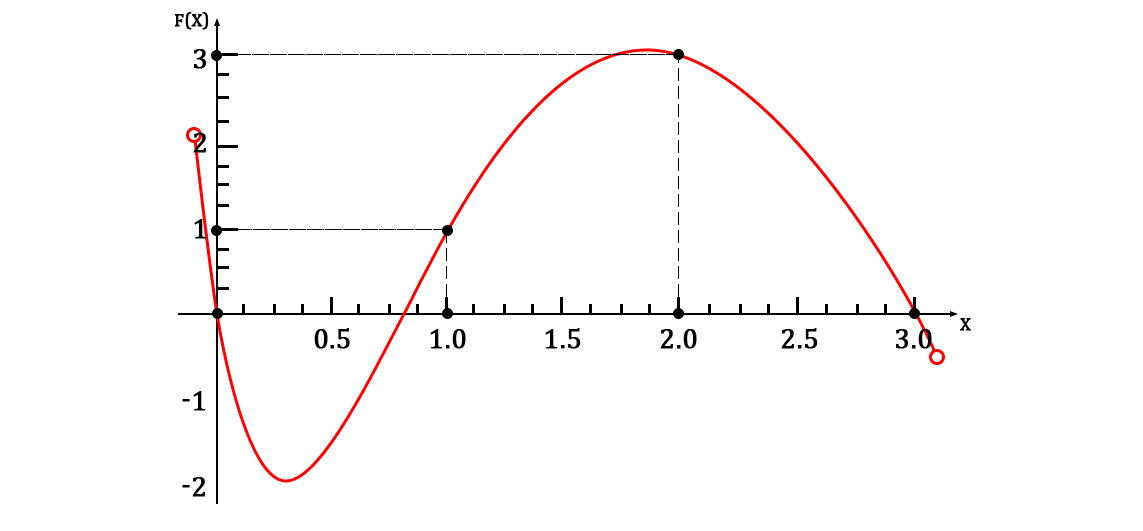
Также, ради наглядности, можно привести аппроксимированную систему решений:

$$

Тогда аппроксимированный вид функции будет следующий:

$$

Разумеется, никто не говорит о том, что полученная функция будет минимальной (тот же полином Лагранжа даст более короткую форму). Однако, данный метод позволяет выразить функцию через набор произвольных функций (правда, имея в виду ограничения, заданные выше по статье).

Различные примеры

На десерт аналогично построим функцию в радикалах:

$$

Составим систему уравнения для нахождения коэффициентов:

$$

Её решение единственно и выглядит следующим образом:

$$

Тогда готовая функция выглядит следующим образом:

$$

Что по совместительтву является полином Лагранжа для данного набора точек (т.к. оный в неявном виде реализует радикальную форму алгоритма из статьи). График на области заданных точек выглядит так:



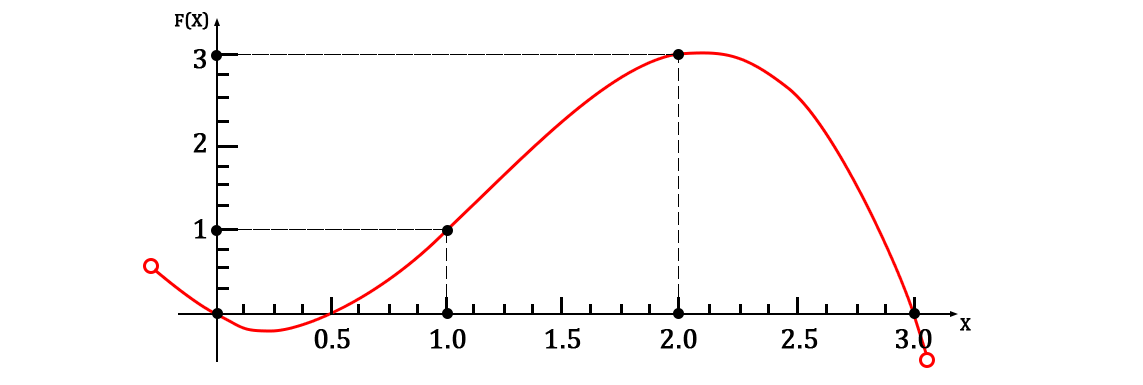
Самым интересным в данной истории является то, что произвольные функции для построения конечной функции можно и нужно комбинировать. Иными словами, функция может быть построена сразу на радикалах и логарифмах, а может и на чем-то другом (показательные функции, факториалы, и т.п. ). Лишь бы полученный набор функций обеспечивал линейную независимость строк при подборе коэффициентов. В общем виде для заданных $$ пар точек это выглядит так:

$$

Где $$ — коэффициенты которые предстоит найти через систему уравнений (СЛАУ), а $$ — некоторые функции, которые обеспечат линейную независимость при нахождении коэффициентов.

А дальше — по алгоритму выше, всё совершенно аналогично. Не забывая о том, что $$ должны быть определены на заданных условием точках.

К примеру можно показать функцию, состоящую из полностью различных базовых функций:

$$

Дабы удовлетворить заданному набору точек, коэффициенты будут в таком случае следующие (найдены строго по алгоритму из статьи):

$$

А сама функция будет такой:

$$

График же будет выглядит практически также как предыдущий (на области заданных точек).
Если хочется более «гладкий» график, то можно посмотреть в сторону факториальной формы, например такой:

$$

Найдем коэффициенты:

$\$\$display\$\$\backslash begin\{cases\}\backslash displaystyle\{2a+b+c+d=0\backslash \backslash \; 6a+2b+c+d=1\backslash \backslash \; 24a+6b+2c+d=3\backslash \backslash \; 120a+24b+6c+d=0\}\; \backslash end\{cases\}\; \backslash Rightarrow\; \backslash begin\{cases\}\backslash displaystyle\{a\; =\; -13/16\backslash \backslash \; b\; =\; 17/4\backslash \backslash \; c\; =\; -3/8\backslash \backslash \; d=-9/4\}\; \backslash end\{cases\}\$\$display\$\$$

Подставим оные в готовую функцию:

$$

А также полюбуемся очень хорошим графиком:

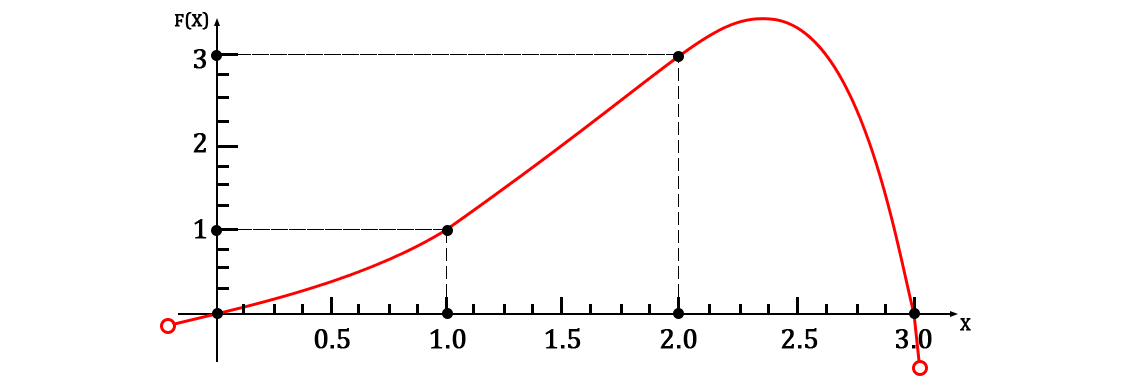
Зачем это нужно?

Да хотя бы для того, чтобы представить себе пучок веревок, стянутых пластиковыми хомутами :)

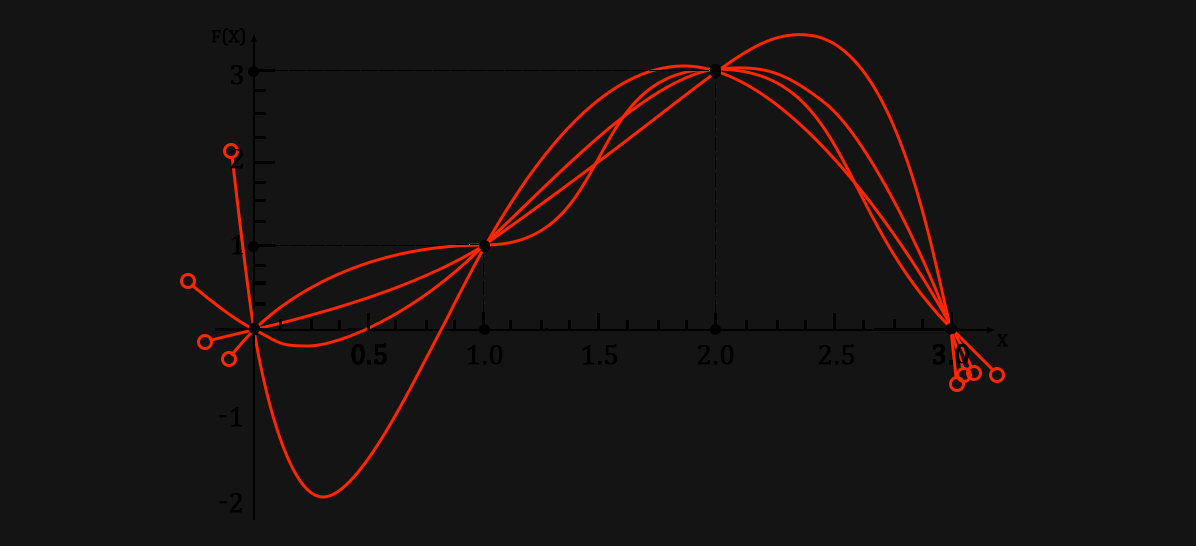
(* Тут мы просто наложили все графики друг на друга)

На этом в рамках текущей статьи все, рекомендую поиграться самостоятельно.

Всего наилучшего,
с вами был Петр.