### Часть 1. Золотое «Ку»
Лет в шесть мне попался в руки дедовский справочник[50] по грузовым автомобилям середины 20-го века. Добротный, напечатанный на гладкой плотной бумаге раритет. Единственное, что вообще осталось на память от деда после распада страны, войн и переездов.


В справочнике содержалось множество интересных ТТХ, так что слово «грузоподъёмность» стало мне знакомо с раннего детства. И когда отец на прогулке упомянул, что любой грузовик весит столько же, сколько увозит сам, я это запомнил. Запомнил и, много позже, заинтересовался.
Отец был прав. Для грузовиков 60-х годов это правило выполняется с довольно удивительной точностью:
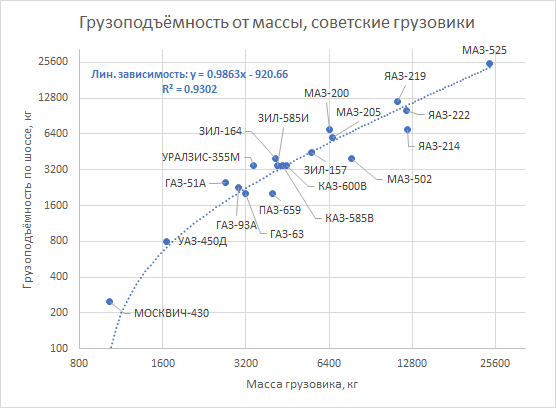
Гораздо любопытнее, что эта закономерность соблюдается и для совершенно непохожих на грузовики транспортных средств.
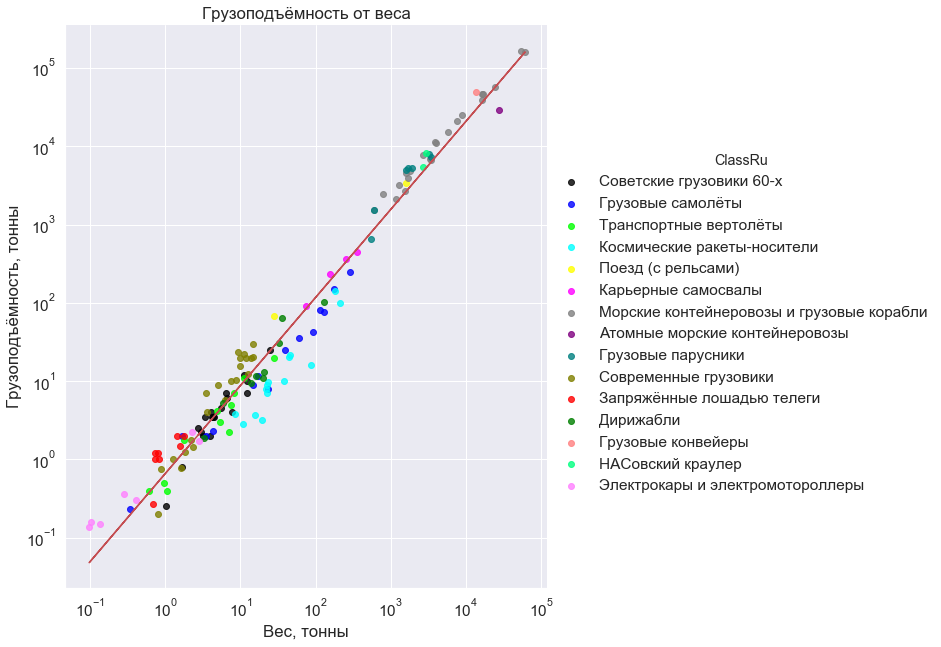
Сначала, хохмы ради, я нанёс на график грузовые самолёты. И удивился. Я стал добавлять другие транспортные средства. Ездящие, плавающие и летающие, построенных в веках 19-м, 20-м, и 21-м, работающие на энергии тепловой, атомной, ветровой и даже конной. Результат? Слабо степенная (показатель 1.125), если не просто линейная, зависимость. На массах от сотни килограмм до шестидесяти тысяч тонн. С отклонениями, конечно, куда же без них, до 10 раз иногда, но на шести порядках масс это, очевидно, мелочи.
Вот она, эта зависимость, жмущаяся к диагонали необъятного пустого поля:

На графике отметились: грузовые самолёты; транспортные вертолёты; дирижабли, современные и начала века; космические ракеты-носители (на низкую орбиту); советские грузовики 60-х; современные карьерные самосвалы; современные грузовики России, США, Китая и Индии; электрические кары и грузовые мотороллеры; поезда (с рельсами); атомные контейнеровозы; морские контейнеровозы и грузовые корабли (не танкеры); парусные грузовые корабли 17-20 веков; конвейерные ленты для передачи руды; насовский тягач для вывоза ракет на старт; и, наконец, телеги, запряжённые лошадью.
Если ввести величину Q, определяемую как масса перевозимого груза по отношению к сухой массе транспортного средства, то вот как она выглядит для каждой из групп:

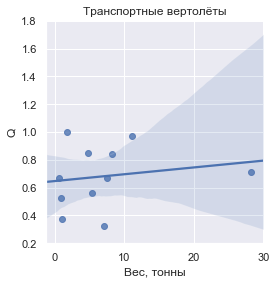

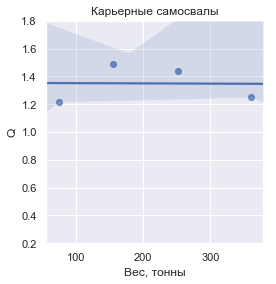




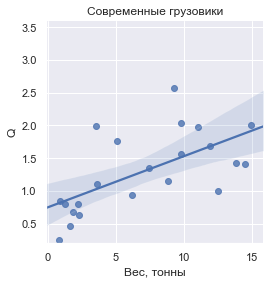


В цифрах значения Q составляют:
Как видно, Q хоть и не везде строго единично, но в рамках каждой группы тяготеет к общему значению, близкому к единице.
Мне это показалось… загадочным. Почему деревянный парусник, алюминиевый электрокар, и атомный контейнеровоз, вмещающий сто тысяч электрокаров, все поднимают более-менее свой вес? Что заставляет нас создавать транспортные средства с качеством Q ? 1 на массах, различающихся в тысячи раз? Проявление ли это свойств мировой физики, земной экономики, ограничение ли это человеческого интеллекта? Насколько универсален этот закон, будет ли он выполняться для цивилизаций с других звёзд? Вопросы глобальные. Вряд ли их удастся разрешить здесь и сейчас. Но вот рассмотреть и понадкусать, сколько получится, можно и нужно. Этим мы и займёмся.
Мировой рекорд[180] подъёма штанги человеком среднего веса превышает 200 кг. Теоретически это означает, что в наше тело заложен запас прочности для рывковых нагрузок по крайней мере до Q = 2.5. Однако это требует таких непомерных сил и тренировок, что в повседневной деятельности никогда не применяется. Целесообразнее фасовать сахар в мешки по 50 килограмм, хотя это и требует вчетверо больше грузчиков или ходок. Заметим, что данная ситуация — результат биологической эволюции, в которой человеческий интеллект участия (почти) не принимал, а следовательно, имеет в ней «алиби».
Физика и инженерия сами по себе высоких Q тоже не запрещают. Вон, водородный турбонасосный агрегат для маршевого двигателя Шаттла, та маленькая штучка справа на картинке, развивает мощность в 54 мегаватта[60] при вполне автомобильной массе в 350 кг:

[Image credit: [10]]
Если, упрощая, оценивать Q по мощности на килограмм массы, то это раз в 100 выше, чем у приличного автомобиля. Только ведь и стоит эта штука почти как ракета! Дешевле сделать 100 автомобилей с Q = 1 и перевезти груз ими, нежели пытаться «запрячь» данный агрегат в колёсную тележку.
Подобные соображения наводят на мысль: причины здесь экономические. Причём не в узком смысле конкретных экономик и стран (ибо наши устройства порождены самыми разными народами и системами), а скорее в смысле «целесообразности усилий». Целесообразности достаточно универсальной, чтобы, видимо, распространяться на очень разные изделия и где-то даже на животных.
Статья написана для сайта https://habr.com. При копировании просьба ссылаться на исходник. Автор статьи Евгений Бобух.
Попробуем исследовать границы этой целесообразности количественно. Поставим вопрос: как стоимость устройства с фиксированной массой зависит от Q? Вот, допустим, есть самосвал весом в 10 тонн, увозит 10 тонн груза. Мы хотим сделать тоже 10-тонный, но увозящий 20 тонн (Q = 2) или даже 50 (Q = 5). На том же уровне развития технологий, того же объёма выпуска. Понятно, что большие нагрузки повысят требования и к материалам (сталь -> титан?), и к двигателям (другие температуры, давления), и к инженерии (меньше допуски на ошибки, более хитрые конструкции). Ясно, что с ростом Q всё будет дороже. Но во сколько раз, по сравнению с десятитонным?
Задача эта, конечно, нетривиальна. Тем не менее, кое-какие оценки для неё можно получить из самых общих соображений. Что мы сейчас и проделаем.
Введём функцию C(Q). Она описывает минимально возможную стоимость устройства с эффективностью Q, выраженную в стоимостях аналогичного устройства той же массы при Q = 1. Что про неё известно?
1. С(1) = 1, по определению.
2. C(Q) — непрерывная функция, по крайней мере, пока разница в массе не измеряется штучными атомами. Интуитивно она кажется достаточно гладкой, чтобы иметь несколько первых производных. Думаю, можно допустить (как и с большинством физических функций), что она вообще аналитическая.
3. C(Q) — строго возрастающая функция. Чем выше качество Q, тем труднее сделать конструкцию, и тем она дороже. Т.е. dC(Q)/dQ > 0 по крайней мере для Q > 0.
4. При Q больше примерно 3-х C(Q) начинает возрастать быстрее, чем линейно. Почему? Потому что мы видим, что людям дешевле сделать три грузовика на десять тонн с Q = 1, чем один на тридцать c Q = 3. Обобщая, пишем: k*C(1) < C(k) при k >?3 — иными словами, C(k) растёт быстрее, чем k, при k >?3.
5. Аналогично, поскольку десять самолётов с Q = 0.1 явно неэкономичнее одного с Q = 1 (ибо строят вторые, а не первые), то для k >?3 имеем: k*C(1/k) > C(1), или C(1/k) > 1/k.
6. Стоимость насоса от Шаттла намекает, что по крайней мере до Q ~ 100 величина C(Q) нарастает ещё не как экспонента с существенным показателем. Иначе бы этот ТНА стоил не миллионы долларов, а эдак от $1020, и вряд ли бы мы вообще его сделали. Т.е. C(100) — это где-то 103 — 108, но никак не 1015.
7. Чему равно C(0)? Это стоимость устройства, которое ещё может сдвинуть с места себя, но неспособно увезти никакой груз. Очевидно, такой «грузовик» дешевле полноценного. Но во сколько раз? История показывает, что скорее в разы, чем в десятки или сотни. От первого самолёта, способного перемещать только себя (Q = 0), до перевозки грузов по воздуху прошло каких-то лет 15. От первых бензиновых автомобилей до вполне приличных грузовиков с Q = 1.5 ([120] + [130]) ненамного больше. Если бы это развитие представляло собой неимоверную сложность, оно вряд ли завершилось бы так быстро. Следовательно, трудность изготовления и стоимость транспортного средства с Q = 0 не должна совсем уж радикально отличаться от оной при Q = 1. Отсюда ожидаем, что C(0) — это где-то 0.1 — 0.5.
8. Имеет ли эта функция смысл при отрицательных Q? Вполне! Грузовик с Q = -0.5 — это такой, который сдвинется с места, только если башенным краном «снять» с него половину его веса. А Q = -1 — это повозка, развивающая нулевую тягу. Способная перевозить груз, только если взять её на буксир. То есть, вообще без двигателя. Очевидно, её стоимость если и не равна нулю, то очень мала. Поэтому положим C(-1) ? 0.
9. А что такое C(-2)? Это стоимость устройства, которое нужно тянуть вверх не менее чем с удвоенным его весом, чтобы сдвинуть! Да, области Q < -1 — это якоря, фундаменты, сваи, тормоза. Устройства, препятствующие движению. Там, конечно, совсем другая динамика и свои законы, но по крайней мере мы видим, что C(Q) не обрывается особенностью при Q < -1, и что в районе Q = -1 у неё минимум, а значит, хотя бы на небольшой окрестности этой точки C(Q) должна вести себя как парабола.
Таким образом, эскизно C(Q) выглядит как-то так:

Разложим C(Q) в ряд Тэйлора в точке Q = -1:
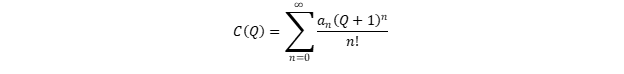
Из свойства (8) следует, что a0 = 0. Свойства (4), (5) и отчасти (9) намекают, что a1 близко к нулю, или уж во всяком случае что его вклад не доминирует на диапазоне 0...3.
А тогда получается, что первый ненулевой член в разложении C(Q) — параболический, и что при Q в районе единиц C(Q) ведёт себя примерно как функция квадратичная или чуть более быстро возрастающая:
C(Q) ? a2*(Q+1)2/2 + O((Q+1)3)
И из [1] следует, что a2 ? 1/2.
Наконец, поскольку по крайней мере до Q ~ 100 функция C(Q) всё ещё не экспоненциальна (свойство (6)), то можно положить её там равной Qp с показателем степени p где-то в районе 2...4. Вряд ли больше.
Вывод: При фиксированной массе стоимость устройства C(Q) возрастает не слабее, чем (Q+1)2/4, но не быстрее, чем примерно O(Q4) [1]
Можно ли взглянуть на реальную зависимость C(Q), чтобы понять, насколько корректен этот вывод? Трудно. Большинство механизмов, изготовляемых человеком — это разные массы, но фиксированные Q в районе единички. Нам же надо наоборот: примерно одинаковая масса, но разные Q. Сначала я надеялся на данные по авиационным двигателям… но работы[70][80] по их ценообразованию устроены очень смешно. Цены двигателей там засекречены, а опубликованы лишь формулы для предсказания и средние ошибки.
К счастью, помощь пришла со стороны легковых автомобилей[150]. Именно у них, при примерно одинаковой массе, встречаются двигатели самых разных мощностей. И хотя мощность — это ещё не перевозимый груз, но при некотором инженерном усилии он ей примерно пропорционален. Что позволяет прикинуть, близка ли наша формула к реальности.
Похоже, что да:

[Источник: [150]]
Синие точки — реальные легковые автомобили. В первом приближении их цена растёт как удельная мощность в степени 2.3.
Красные точки — цена, рассчитанная по формуле [1], исходя из предположения, что Q = 1 соответствует наиболее дешёвым за килограмм легковушкам в диапазоне $20-30 тысяч. Видно, что формула действительно даёт неплохую оценку C(Q) снизу (куда мы и целились).
При взгляде на массу этих вкусных точек возникает сильный соблазн: провести через них C(Q) и, таким образом, исследовать зависимость непосредственно. Делать этого нельзя. Главным образом потому, что цена легковушки определяется не только её тяговыми характеристиками. Трудно вообразить себе машину за сто килобаксов, в которой нет самого хорошего кондиционера, самых удобных кресел и «платиновой пепельницы с родиевой окантовкой». А всё это стоит денег, не имеющих никакого отношения к нашей C(Q). Однако вот нижняя «ветвь» автомобилей, проходящая почти в точности по рассчитанной C(Q), выглядит интересно. Смею допустить, что это — как раз машины без наворотов. Где «не шашечки, а чтобы ехать». Но дороже примерно $100K за автомобиль таких уже нет.
Статья написана для сайта https://habr.com. При копировании просьба ссылаться на исходник. Автор статьи Евгений Бобух.
Итак, стоимости устройств с высокими Q мы, хотя бы по порядку величины, прикидывать умеем. Зачем это было надо?
А вот зачем. Взглянём на первую ступень космического носителя. Ну вот хотя бы Протона-М[110], для конкретности. Она — почти полноценное транспортное средство, с двигателями, системой управления, приличным запасом прочности и сухой массой в 31 тонну. При этом на старте ракеты она тащит на своём горбу не только полезную нагрузку, но и всё топливо, все верхние ступени, и, конечно же, себя. В сумме — 683 тонны. Плюс стартовая перегрузка, итого (эффективно) 1068 тонн нагрузки! С точки зрения первой ступени она работает в жутком режиме Q = (1068/31) = 34.4! Это эквивалент 50 тонн груза, наваленного на легковушку.
И мы знаем, что стоимость устройства с высоким Q как минимум в (Q+1)2/4 раз выше, чем чего-то аналогичного с Q ? 1. Для «Протона» это составляет… 313 раз.
То есть, «Протон» должен обходиться раз в 300 дороже похожего устройства с Q = 1. И эта цифра мало зависит от прогресса и технологий. Ибо как только «британские учёные» изобретают супер-сплав, делающий ракету дешевле, тут же дешевеют и наземные двигатели. Поэтому химическая ракета, даже многоразовая, будет всегда очень дорога. Как ни крути.
Хорошо. Допустим, в 300 раз. Но по сравнению всё-таки с чем? Неплохо бы сверить наши выкладки с какими-нибудь объективно существующими устройствами, для исключения грубых ошибок?
К сожалению, тридцатонных ракет с Q = 1 нет. Но есть приблизительные аналоги, пригодные для сравнения:
Вроде, мы не совсем уж оторваны от реальности.
Подведём итоги. Поскольку ракеты, даже многоразовые, стоят на 2-3 порядка дороже грузовиков, то и любое космическое поселение из наземных материалов тоже обойдётся в 100-1000 раз дороже наземного аналога. Это очень высокий барьер на освоение.
Ракеты же дороги потому, что они очень тяжёлые и вынуждены работать при нездорово высоких Q. Но почему ракеты тяжёлые? Ответ (который несколько глубже, чем формула Циолковского) мы рассмотрим во второй части.
Продолжение.
Update: несколько человек пытались мне указать на неоднозначности с учётом топлива при рассмотрении ракет. Я об этом подумал. И понял, что в статье действительно есть некоторая неточность. Рассмотренная в комментарии здесь.

Лет в шесть мне попался в руки дедовский справочник[50] по грузовым автомобилям середины 20-го века. Добротный, напечатанный на гладкой плотной бумаге раритет. Единственное, что вообще осталось на память от деда после распада страны, войн и переездов.


В справочнике содержалось множество интересных ТТХ, так что слово «грузоподъёмность» стало мне знакомо с раннего детства. И когда отец на прогулке упомянул, что любой грузовик весит столько же, сколько увозит сам, я это запомнил. Запомнил и, много позже, заинтересовался.
Отец был прав. Для грузовиков 60-х годов это правило выполняется с довольно удивительной точностью:

Гораздо любопытнее, что эта закономерность соблюдается и для совершенно непохожих на грузовики транспортных средств.
Сначала, хохмы ради, я нанёс на график грузовые самолёты. И удивился. Я стал добавлять другие транспортные средства. Ездящие, плавающие и летающие, построенных в веках 19-м, 20-м, и 21-м, работающие на энергии тепловой, атомной, ветровой и даже конной. Результат? Слабо степенная (показатель 1.125), если не просто линейная, зависимость. На массах от сотни килограмм до шестидесяти тысяч тонн. С отклонениями, конечно, куда же без них, до 10 раз иногда, но на шести порядках масс это, очевидно, мелочи.
Вот она, эта зависимость, жмущаяся к диагонали необъятного пустого поля:

На графике отметились: грузовые самолёты; транспортные вертолёты; дирижабли, современные и начала века; космические ракеты-носители (на низкую орбиту); советские грузовики 60-х; современные карьерные самосвалы; современные грузовики России, США, Китая и Индии; электрические кары и грузовые мотороллеры; поезда (с рельсами); атомные контейнеровозы; морские контейнеровозы и грузовые корабли (не танкеры); парусные грузовые корабли 17-20 веков; конвейерные ленты для передачи руды; насовский тягач для вывоза ракет на старт; и, наконец, телеги, запряжённые лошадью.
Если ввести величину Q, определяемую как масса перевозимого груза по отношению к сухой массе транспортного средства, то вот как она выглядит для каждой из групп:











В цифрах значения Q составляют:
| Класс средств | Среднее Q | Среднеквадратичное отклонение Q |
| Грузовые самолёты | 0.667091 | ± 0.206162 |
| Транспортные вертолёты | 0.681605 | ± 0.225062 |
| Дирижабли, современные и начала века | 0.842673 | ± 0.374622 |
| Космические ракеты-носители (низкая орбита) | 0.372446 | ± 0.155810 |
| Советские грузовики 60-х | 0.777435 | ± 0.232425 |
| Современные карьерные самосвалы | 1.349610 | ± 0.136840 |
| Современные грузовики России, США, Индии, Китая | 1.293679 | ± 0.604313 |
| Электрические карты и грузовые мотороллеры | 1.098433 | ± 0.343791 |
| Поезд (с рельсами) | 2.275989 | ± 0.205999 |
| Атомные контейнеровозы | 1.035233 | ± NA |
| Морские контейнеровозы и грузовые корабли (не танкеры) | 2.556004 | ± 0.378040 |
| Парусные грузовые корабли 17-20 веков | 2.488461 | ± 0.671785 |
| Грузовые конвейерные ленты | 3.703704 | ± NA |
| Насовский тягач для вывоза ракет на старт | 2.355919 | ± 0.525174 |
| Телеги, запряжённые лошадью | 1.203061 | ± 0.389183 |
Как видно, Q хоть и не везде строго единично, но в рамках каждой группы тяготеет к общему значению, близкому к единице.
Мне это показалось… загадочным. Почему деревянный парусник, алюминиевый электрокар, и атомный контейнеровоз, вмещающий сто тысяч электрокаров, все поднимают более-менее свой вес? Что заставляет нас создавать транспортные средства с качеством Q ? 1 на массах, различающихся в тысячи раз? Проявление ли это свойств мировой физики, земной экономики, ограничение ли это человеческого интеллекта? Насколько универсален этот закон, будет ли он выполняться для цивилизаций с других звёзд? Вопросы глобальные. Вряд ли их удастся разрешить здесь и сейчас. Но вот рассмотреть и понадкусать, сколько получится, можно и нужно. Этим мы и займёмся.
Мировой рекорд[180] подъёма штанги человеком среднего веса превышает 200 кг. Теоретически это означает, что в наше тело заложен запас прочности для рывковых нагрузок по крайней мере до Q = 2.5. Однако это требует таких непомерных сил и тренировок, что в повседневной деятельности никогда не применяется. Целесообразнее фасовать сахар в мешки по 50 килограмм, хотя это и требует вчетверо больше грузчиков или ходок. Заметим, что данная ситуация — результат биологической эволюции, в которой человеческий интеллект участия (почти) не принимал, а следовательно, имеет в ней «алиби».
Физика и инженерия сами по себе высоких Q тоже не запрещают. Вон, водородный турбонасосный агрегат для маршевого двигателя Шаттла, та маленькая штучка справа на картинке, развивает мощность в 54 мегаватта[60] при вполне автомобильной массе в 350 кг:

[Image credit: [10]]
Если, упрощая, оценивать Q по мощности на килограмм массы, то это раз в 100 выше, чем у приличного автомобиля. Только ведь и стоит эта штука почти как ракета! Дешевле сделать 100 автомобилей с Q = 1 и перевезти груз ими, нежели пытаться «запрячь» данный агрегат в колёсную тележку.
Подобные соображения наводят на мысль: причины здесь экономические. Причём не в узком смысле конкретных экономик и стран (ибо наши устройства порождены самыми разными народами и системами), а скорее в смысле «целесообразности усилий». Целесообразности достаточно универсальной, чтобы, видимо, распространяться на очень разные изделия и где-то даже на животных.
Статья написана для сайта https://habr.com. При копировании просьба ссылаться на исходник. Автор статьи Евгений Бобух.
Попробуем исследовать границы этой целесообразности количественно. Поставим вопрос: как стоимость устройства с фиксированной массой зависит от Q? Вот, допустим, есть самосвал весом в 10 тонн, увозит 10 тонн груза. Мы хотим сделать тоже 10-тонный, но увозящий 20 тонн (Q = 2) или даже 50 (Q = 5). На том же уровне развития технологий, того же объёма выпуска. Понятно, что большие нагрузки повысят требования и к материалам (сталь -> титан?), и к двигателям (другие температуры, давления), и к инженерии (меньше допуски на ошибки, более хитрые конструкции). Ясно, что с ростом Q всё будет дороже. Но во сколько раз, по сравнению с десятитонным?
Задача эта, конечно, нетривиальна. Тем не менее, кое-какие оценки для неё можно получить из самых общих соображений. Что мы сейчас и проделаем.
Введём функцию C(Q). Она описывает минимально возможную стоимость устройства с эффективностью Q, выраженную в стоимостях аналогичного устройства той же массы при Q = 1. Что про неё известно?
1. С(1) = 1, по определению.
2. C(Q) — непрерывная функция, по крайней мере, пока разница в массе не измеряется штучными атомами. Интуитивно она кажется достаточно гладкой, чтобы иметь несколько первых производных. Думаю, можно допустить (как и с большинством физических функций), что она вообще аналитическая.
3. C(Q) — строго возрастающая функция. Чем выше качество Q, тем труднее сделать конструкцию, и тем она дороже. Т.е. dC(Q)/dQ > 0 по крайней мере для Q > 0.
4. При Q больше примерно 3-х C(Q) начинает возрастать быстрее, чем линейно. Почему? Потому что мы видим, что людям дешевле сделать три грузовика на десять тонн с Q = 1, чем один на тридцать c Q = 3. Обобщая, пишем: k*C(1) < C(k) при k >?3 — иными словами, C(k) растёт быстрее, чем k, при k >?3.
5. Аналогично, поскольку десять самолётов с Q = 0.1 явно неэкономичнее одного с Q = 1 (ибо строят вторые, а не первые), то для k >?3 имеем: k*C(1/k) > C(1), или C(1/k) > 1/k.
6. Стоимость насоса от Шаттла намекает, что по крайней мере до Q ~ 100 величина C(Q) нарастает ещё не как экспонента с существенным показателем. Иначе бы этот ТНА стоил не миллионы долларов, а эдак от $1020, и вряд ли бы мы вообще его сделали. Т.е. C(100) — это где-то 103 — 108, но никак не 1015.
7. Чему равно C(0)? Это стоимость устройства, которое ещё может сдвинуть с места себя, но неспособно увезти никакой груз. Очевидно, такой «грузовик» дешевле полноценного. Но во сколько раз? История показывает, что скорее в разы, чем в десятки или сотни. От первого самолёта, способного перемещать только себя (Q = 0), до перевозки грузов по воздуху прошло каких-то лет 15. От первых бензиновых автомобилей до вполне приличных грузовиков с Q = 1.5 ([120] + [130]) ненамного больше. Если бы это развитие представляло собой неимоверную сложность, оно вряд ли завершилось бы так быстро. Следовательно, трудность изготовления и стоимость транспортного средства с Q = 0 не должна совсем уж радикально отличаться от оной при Q = 1. Отсюда ожидаем, что C(0) — это где-то 0.1 — 0.5.
8. Имеет ли эта функция смысл при отрицательных Q? Вполне! Грузовик с Q = -0.5 — это такой, который сдвинется с места, только если башенным краном «снять» с него половину его веса. А Q = -1 — это повозка, развивающая нулевую тягу. Способная перевозить груз, только если взять её на буксир. То есть, вообще без двигателя. Очевидно, её стоимость если и не равна нулю, то очень мала. Поэтому положим C(-1) ? 0.
9. А что такое C(-2)? Это стоимость устройства, которое нужно тянуть вверх не менее чем с удвоенным его весом, чтобы сдвинуть! Да, области Q < -1 — это якоря, фундаменты, сваи, тормоза. Устройства, препятствующие движению. Там, конечно, совсем другая динамика и свои законы, но по крайней мере мы видим, что C(Q) не обрывается особенностью при Q < -1, и что в районе Q = -1 у неё минимум, а значит, хотя бы на небольшой окрестности этой точки C(Q) должна вести себя как парабола.
Таким образом, эскизно C(Q) выглядит как-то так:

Разложим C(Q) в ряд Тэйлора в точке Q = -1:
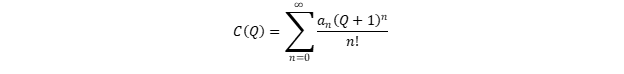
Из свойства (8) следует, что a0 = 0. Свойства (4), (5) и отчасти (9) намекают, что a1 близко к нулю, или уж во всяком случае что его вклад не доминирует на диапазоне 0...3.
А тогда получается, что первый ненулевой член в разложении C(Q) — параболический, и что при Q в районе единиц C(Q) ведёт себя примерно как функция квадратичная или чуть более быстро возрастающая:
C(Q) ? a2*(Q+1)2/2 + O((Q+1)3)
И из [1] следует, что a2 ? 1/2.
Наконец, поскольку по крайней мере до Q ~ 100 функция C(Q) всё ещё не экспоненциальна (свойство (6)), то можно положить её там равной Qp с показателем степени p где-то в районе 2...4. Вряд ли больше.
Вывод: При фиксированной массе стоимость устройства C(Q) возрастает не слабее, чем (Q+1)2/4, но не быстрее, чем примерно O(Q4) [1]
Можно ли взглянуть на реальную зависимость C(Q), чтобы понять, насколько корректен этот вывод? Трудно. Большинство механизмов, изготовляемых человеком — это разные массы, но фиксированные Q в районе единички. Нам же надо наоборот: примерно одинаковая масса, но разные Q. Сначала я надеялся на данные по авиационным двигателям… но работы[70][80] по их ценообразованию устроены очень смешно. Цены двигателей там засекречены, а опубликованы лишь формулы для предсказания и средние ошибки.
К счастью, помощь пришла со стороны легковых автомобилей[150]. Именно у них, при примерно одинаковой массе, встречаются двигатели самых разных мощностей. И хотя мощность — это ещё не перевозимый груз, но при некотором инженерном усилии он ей примерно пропорционален. Что позволяет прикинуть, близка ли наша формула к реальности.
Похоже, что да:

[Источник: [150]]
Синие точки — реальные легковые автомобили. В первом приближении их цена растёт как удельная мощность в степени 2.3.
Красные точки — цена, рассчитанная по формуле [1], исходя из предположения, что Q = 1 соответствует наиболее дешёвым за килограмм легковушкам в диапазоне $20-30 тысяч. Видно, что формула действительно даёт неплохую оценку C(Q) снизу (куда мы и целились).
При взгляде на массу этих вкусных точек возникает сильный соблазн: провести через них C(Q) и, таким образом, исследовать зависимость непосредственно. Делать этого нельзя. Главным образом потому, что цена легковушки определяется не только её тяговыми характеристиками. Трудно вообразить себе машину за сто килобаксов, в которой нет самого хорошего кондиционера, самых удобных кресел и «платиновой пепельницы с родиевой окантовкой». А всё это стоит денег, не имеющих никакого отношения к нашей C(Q). Однако вот нижняя «ветвь» автомобилей, проходящая почти в точности по рассчитанной C(Q), выглядит интересно. Смею допустить, что это — как раз машины без наворотов. Где «не шашечки, а чтобы ехать». Но дороже примерно $100K за автомобиль таких уже нет.
Статья написана для сайта https://habr.com. При копировании просьба ссылаться на исходник. Автор статьи Евгений Бобух.
Итак, стоимости устройств с высокими Q мы, хотя бы по порядку величины, прикидывать умеем. Зачем это было надо?
А вот зачем. Взглянём на первую ступень космического носителя. Ну вот хотя бы Протона-М[110], для конкретности. Она — почти полноценное транспортное средство, с двигателями, системой управления, приличным запасом прочности и сухой массой в 31 тонну. При этом на старте ракеты она тащит на своём горбу не только полезную нагрузку, но и всё топливо, все верхние ступени, и, конечно же, себя. В сумме — 683 тонны. Плюс стартовая перегрузка, итого (эффективно) 1068 тонн нагрузки! С точки зрения первой ступени она работает в жутком режиме Q = (1068/31) = 34.4! Это эквивалент 50 тонн груза, наваленного на легковушку.
И мы знаем, что стоимость устройства с высоким Q как минимум в (Q+1)2/4 раз выше, чем чего-то аналогичного с Q ? 1. Для «Протона» это составляет… 313 раз.
То есть, «Протон» должен обходиться раз в 300 дороже похожего устройства с Q = 1. И эта цифра мало зависит от прогресса и технологий. Ибо как только «британские учёные» изобретают супер-сплав, делающий ракету дешевле, тут же дешевеют и наземные двигатели. Поэтому химическая ракета, даже многоразовая, будет всегда очень дорога. Как ни крути.
Хорошо. Допустим, в 300 раз. Но по сравнению всё-таки с чем? Неплохо бы сверить наши выкладки с какими-нибудь объективно существующими устройствами, для исключения грубых ошибок?
К сожалению, тридцатонных ракет с Q = 1 нет. Но есть приблизительные аналоги, пригодные для сравнения:
- Самый первый — карьерный самосвал. Да, не ракета. Но всё-таки тоже тепловой двигатель, не совсем тривиальная инженерия, и одно из самых дешёвых средств для перевозки грузов. И если уж мы говорим об освоении космоса, то не грузовик ли должен быть прообразом бизнес-модели космического извозчика? Так что попробуем, хотя бы для общей прикидки. Вот 30-тонный Белаз-7540. Рыночная цена[140] — 3.7 миллиона рублей, т.е. $62K. Для «Протона» это пересчитывается в стоимость первой ступени в районе $19 миллионов. Википедия обозначает[100] стоимость пуска как $65 миллионов. Довольно близко, учитывая, что в эту сумму входит ещё много чего, кроме цены самой первой ступени.
- В [160] описана экспериментальная ракетная платформа на рельсах. Массой под 10 тонн, пять ступеней, разгоняется до 4 км/с. Цена 750 килобаксов. Судя по опубликованным картинкам и параметрам, работает это устройство где-то при Q = 10. Не единица, но всё-таки и не 34. Если отталкиваться от этих цифр, первая ступень «Протона» должна стоить где-то $23 миллиона.
- Вообще, когда я пытаюсь представить себе ракету с Q = 1, перед мысленным взором возникает этакая здоровенная болванка с ма-аленькой выемкой, наполненной порохом. Порох выгорает и толкает болванку вперёд. Совсем чуток, сильно так не разгонишься. Я два дня мусолил эту картину, пока не понял, что она мне напоминает. Это же… пневматический молот! Где газ расширяется и толкает болванку. Предельная бастардизация идеи реактивного двигателя, ещё сохраняющая какое-то родство. Что ж, ищем. Ага, вот[170] пневматический молот Stanko M212. Вес болванки 2 тонны, всей конструкции — 58.3 тонн. Q системы, таким образом, составляет скромненькие 0.034. Продаётся за 40 тысяч евро. Если экстраполировать стоимость этой шутки на Q = 34.4 по формуле [1], то получится… 47 миллионов евро. Или 24 миллиона в пропорции за 30 тонн.
Вроде, мы не совсем уж оторваны от реальности.
Подведём итоги. Поскольку ракеты, даже многоразовые, стоят на 2-3 порядка дороже грузовиков, то и любое космическое поселение из наземных материалов тоже обойдётся в 100-1000 раз дороже наземного аналога. Это очень высокий барьер на освоение.
Ракеты же дороги потому, что они очень тяжёлые и вынуждены работать при нездорово высоких Q. Но почему ракеты тяжёлые? Ответ (который несколько глубже, чем формула Циолковского) мы рассмотрим во второй части.
Продолжение.
Update: несколько человек пытались мне указать на неоднозначности с учётом топлива при рассмотрении ракет. Я об этом подумал. И понял, что в статье действительно есть некоторая неточность. Рассмотренная в комментарии здесь.
Про данные
Желающие самостоятельно проанализировать данные могут найти их (вместе с источниками) здесь в формате CSV. (Кстати, какие на Хабре есть лучшие варианты, кроме выкладывания файла на сторонний хостинг?) При работе с ними следует учесть следующее.
1. Рассматривались только грузовые транспортные средства. Пассажирская Тесла с вместимостью багажника в 70 кг — не грузовик. Грузовые фургоны тоже (почти) исключены — у них средства защиты груза вносят существенные искажения.
2. С советскими грузовиками работать было одно удовольствие. Вот вес, вот допустимая нагрузка, всё чётко. С современными, особенно американскими — беда. Мало кто публикует их максимальную грузоподъёмность. Вместо этого есть законы, разрешающие ту или иную нагрузку для каждого типа бизнеса и дорог. Плюс приписка к грузовику: «удовлетворяет стандарту № такой-то, § такой-то». Полная, разгромная победа бюрократии над физической реальностью. В тех случаях, когда грузоподъёмность всё-таки публикуется, она сплошь и рядом взятаот балды из маркетинговых соображений. Строишь график — а там явная «ёлочка», пардон, линейка продуктов. По этой причине, увы, данные современных грузовиков более зашумлены (± 0.60), нежели старых (± 0.23). Положение отчасти спасли Китай, Россия и Индия: у них ТТХ грузовиков по-прежнему легкодоступны.
3. Самые лёгкие электрические кары и мотоциклы весят зачастую по 30-70 кг, перевозя при этом по 200-400 кг груза. На первый взгляд, это выглядит как Q в районе десятки. Но я подумал и кое-что осознал. Все эти транспортные средства не ездят без человека. Более того, человек в них выполняет ещё и структурно-силовую и балансирующую роль. Он в них — не полезная нагрузка, без которой можно и уехать, а неотъемлемая запчасть. Поэтому и массу их надо считать с водителем (+80 кг). А это уже 100-150 кг. Аналогичная поправка вносилась в характеристики конных экипажей, с массой лошади принятой за 500 кг.
4. Массу поезда я считал с массой подстилающих его рельсов. Ибо, в отличие от прочих транспортных средств, перемещаться поезд может только по рельсам, а они весят существенно и держат транспортную нагрузку. Как гусеницы у бульдозера. Только не носимые с собой. При этом на сами рельсы, вагоны и электровозы существует куча запутанных спецификаций, в которых я не факт, что правильно разобрался.
5. Атомный грузовой ледокол в мире один: российский Севморпуть[600], так что и точка в этой группе лишь одна.
6. С грузовыми мореходными судами тоже не всё просто. Для большинства из них не публикуется ни максимальная масса груза, ни пустая масса конструкции. Для второго, правда, есть всё-таки термин: LWT — Light Weight Tonnage, и его значения изредка встречается на корабельных аукционах (типа [610] и [620]). Долгим ручным вычитыванием этих сайтов я надёргал цифр по LWT, но как быть с перевозимым грузом? Вместо него обычно используется величина DWT (Deadweight Tonnage), представляющая собой полный максимально возможный вес корабля. В который входят не только вес груза, но и конструкции, топлива, вспомогательных жидкостей, и ещё каких-то мелочей. Пошарившись по разным сайтам, я установил, что на практике предельный вес груза обычно составляет 85% от (DWT — LWT), с разбросом в 65-90%. Этим пришлось и удовлетвориться. Так что грузоподъёмность считалась как Г = 0.85*(DWT — LWT). Что, возможно, внесло погрешность до 30%.
7. По космическим носителям я опирался в основном на [110]. Там лежит разбивка многих ракет по ступеням и их массам. К сожалению, иногда с пометкой, что масса ступени включает остатки несгоревшего топлива, которые толком неизвестны. По этой причине величина Q для ракет, возможно, занижена процентов на 10.
8. Были ли транспортные средства, в эту картину не вписывающиеся? Конечно. Во-первых, негрузовые. Танки. Пассажирские автомобили, круизные пароходы. У них Q существенно меньше единицы. С последними всё понятно: их цель — не груз увезти, а людей, да ещё с комфортом. Вес средств комфорта портит им картину. Во-вторых, сюда не вписываются танкеры, у которых Q нередко достигает 3-8 единиц. Но у танкеров особенный и очень «удобный» груз, допускающий равномерное распределение нагрузки по корпусу и удержание её не столько собственной прочностью, сколько внешним давлением моря. На суше аналогом этого был бы грузовик с «костылями», но таких нет, сравнивать не с чем, а потому танкеры я на графике не указал (хотя вот упоминаю здесь).
Желающие самостоятельно проанализировать данные могут найти их (вместе с источниками) здесь в формате CSV. (Кстати, какие на Хабре есть лучшие варианты, кроме выкладывания файла на сторонний хостинг?) При работе с ними следует учесть следующее.
1. Рассматривались только грузовые транспортные средства. Пассажирская Тесла с вместимостью багажника в 70 кг — не грузовик. Грузовые фургоны тоже (почти) исключены — у них средства защиты груза вносят существенные искажения.
2. С советскими грузовиками работать было одно удовольствие. Вот вес, вот допустимая нагрузка, всё чётко. С современными, особенно американскими — беда. Мало кто публикует их максимальную грузоподъёмность. Вместо этого есть законы, разрешающие ту или иную нагрузку для каждого типа бизнеса и дорог. Плюс приписка к грузовику: «удовлетворяет стандарту № такой-то, § такой-то». Полная, разгромная победа бюрократии над физической реальностью. В тех случаях, когда грузоподъёмность всё-таки публикуется, она сплошь и рядом взята
3. Самые лёгкие электрические кары и мотоциклы весят зачастую по 30-70 кг, перевозя при этом по 200-400 кг груза. На первый взгляд, это выглядит как Q в районе десятки. Но я подумал и кое-что осознал. Все эти транспортные средства не ездят без человека. Более того, человек в них выполняет ещё и структурно-силовую и балансирующую роль. Он в них — не полезная нагрузка, без которой можно и уехать, а неотъемлемая запчасть. Поэтому и массу их надо считать с водителем (+80 кг). А это уже 100-150 кг. Аналогичная поправка вносилась в характеристики конных экипажей, с массой лошади принятой за 500 кг.
4. Массу поезда я считал с массой подстилающих его рельсов. Ибо, в отличие от прочих транспортных средств, перемещаться поезд может только по рельсам, а они весят существенно и держат транспортную нагрузку. Как гусеницы у бульдозера. Только не носимые с собой. При этом на сами рельсы, вагоны и электровозы существует куча запутанных спецификаций, в которых я не факт, что правильно разобрался.
5. Атомный грузовой ледокол в мире один: российский Севморпуть[600], так что и точка в этой группе лишь одна.
6. С грузовыми мореходными судами тоже не всё просто. Для большинства из них не публикуется ни максимальная масса груза, ни пустая масса конструкции. Для второго, правда, есть всё-таки термин: LWT — Light Weight Tonnage, и его значения изредка встречается на корабельных аукционах (типа [610] и [620]). Долгим ручным вычитыванием этих сайтов я надёргал цифр по LWT, но как быть с перевозимым грузом? Вместо него обычно используется величина DWT (Deadweight Tonnage), представляющая собой полный максимально возможный вес корабля. В который входят не только вес груза, но и конструкции, топлива, вспомогательных жидкостей, и ещё каких-то мелочей. Пошарившись по разным сайтам, я установил, что на практике предельный вес груза обычно составляет 85% от (DWT — LWT), с разбросом в 65-90%. Этим пришлось и удовлетвориться. Так что грузоподъёмность считалась как Г = 0.85*(DWT — LWT). Что, возможно, внесло погрешность до 30%.
7. По космическим носителям я опирался в основном на [110]. Там лежит разбивка многих ракет по ступеням и их массам. К сожалению, иногда с пометкой, что масса ступени включает остатки несгоревшего топлива, которые толком неизвестны. По этой причине величина Q для ракет, возможно, занижена процентов на 10.
8. Были ли транспортные средства, в эту картину не вписывающиеся? Конечно. Во-первых, негрузовые. Танки. Пассажирские автомобили, круизные пароходы. У них Q существенно меньше единицы. С последними всё понятно: их цель — не груз увезти, а людей, да ещё с комфортом. Вес средств комфорта портит им картину. Во-вторых, сюда не вписываются танкеры, у которых Q нередко достигает 3-8 единиц. Но у танкеров особенный и очень «удобный» груз, допускающий равномерное распределение нагрузки по корпусу и удержание её не столько собственной прочностью, сколько внешним давлением моря. На суше аналогом этого был бы грузовик с «костылями», но таких нет, сравнивать не с чем, а потому танкеры я на графике не указал (хотя вот упоминаю здесь).
Ссылки
[10] Схема SSME: http://www.jht.com/icuf/Space-Science/LiquidRockets/PT-04-125.htm
[50] А. П. Рунова, А. А. Вагнер. ГРУЗОВЫЕ АВТОМОБИЛИ. КАТАЛОГ. Типография ЦИНТИМАШ, 1960 г.
[60] Power-to-weight ratios: https://en.wikipedia.org/wiki/Power-to-weight_ratio#Heat_engines_and_heat_pumps
[70] Development and Production Cost Estimating Relationships for Aircraft Turbine Engines by John Birkler, Jeffrey B. Garfinkle, Kenneth E. Marks, https://www.rand.org/content/dam/rand/pubs/notes/2005/N1882.pdf
[80] Military Jet Engine Acquisition (Technology Basics and Cost-Estimating Methodology), Obaid Younossi, Mark V. Arena, Richard M. Moore
Mark Lorell, Joanna Mason, John C. Graser, https://www.rand.org/content/dam/rand/pubs/monograph_reports/2005/MR1596.pdf
[100] Стоимость пуска Протона-М: https://en.wikipedia.org/wiki/Proton-M
[110] Данные по ступеням «Протона»: http://www.spacelaunchreport.com/proton.html
[120] Ford TT curb weight: https://www.conceptcarz.com/s13963/ford-model-tt-type-c.aspx
[130] Ford TT load capacity: https://en.wikipedia.org/wiki/Ford_Model_TT
[140] Цена на Белаз-7540: http://www.raise.ru/market/mining/haul-trucks/id-market_43697/
[150] Подборка ста с лишним автомобилей с данными по мощности, весу, цене, и удельным параметрам: https://oppositelock.kinja.com/whats-the-best-power-weight-ratio-per-dollar-1699756090 (автор проделал нетривиальную работу, но почему-то гадает, нужны ли эти данные. Да ещё как нужны!)
[160] Ракетные сани: http://www.impactlab.net/2006/01/15/the-fastest-rocket-sled-on-earth/
[170] Пневматический молот https://www.machineseeker.com/Air-steam-Forging-Hammer-double-action-Stanko-M212-RAM-2000kg/i-3521173
[180] Мировые рекорды в тяжёлой атлетике: https://ru.wikipedia.org/wiki/%D0%9C%D0%B8%D1%80%D0%BE%D0%B2%D1%8B%D0%B5_%D1%80%D0%B5%D0%BA%D0%BE%D1%80%D0%B4%D1%8B_%D0%B2_%D1%82%D1%8F%D0%B6%D1%91%D0%BB%D0%BE%D0%B9_%D0%B0%D1%82%D0%BB%D0%B5%D1%82%D0%B8%D0%BA%D0%B5
[10] Схема SSME: http://www.jht.com/icuf/Space-Science/LiquidRockets/PT-04-125.htm
[50] А. П. Рунова, А. А. Вагнер. ГРУЗОВЫЕ АВТОМОБИЛИ. КАТАЛОГ. Типография ЦИНТИМАШ, 1960 г.
[60] Power-to-weight ratios: https://en.wikipedia.org/wiki/Power-to-weight_ratio#Heat_engines_and_heat_pumps
[70] Development and Production Cost Estimating Relationships for Aircraft Turbine Engines by John Birkler, Jeffrey B. Garfinkle, Kenneth E. Marks, https://www.rand.org/content/dam/rand/pubs/notes/2005/N1882.pdf
[80] Military Jet Engine Acquisition (Technology Basics and Cost-Estimating Methodology), Obaid Younossi, Mark V. Arena, Richard M. Moore
Mark Lorell, Joanna Mason, John C. Graser, https://www.rand.org/content/dam/rand/pubs/monograph_reports/2005/MR1596.pdf
[100] Стоимость пуска Протона-М: https://en.wikipedia.org/wiki/Proton-M
[110] Данные по ступеням «Протона»: http://www.spacelaunchreport.com/proton.html
[120] Ford TT curb weight: https://www.conceptcarz.com/s13963/ford-model-tt-type-c.aspx
[130] Ford TT load capacity: https://en.wikipedia.org/wiki/Ford_Model_TT
[140] Цена на Белаз-7540: http://www.raise.ru/market/mining/haul-trucks/id-market_43697/
[150] Подборка ста с лишним автомобилей с данными по мощности, весу, цене, и удельным параметрам: https://oppositelock.kinja.com/whats-the-best-power-weight-ratio-per-dollar-1699756090 (автор проделал нетривиальную работу, но почему-то гадает, нужны ли эти данные. Да ещё как нужны!)
[160] Ракетные сани: http://www.impactlab.net/2006/01/15/the-fastest-rocket-sled-on-earth/
[170] Пневматический молот https://www.machineseeker.com/Air-steam-Forging-Hammer-double-action-Stanko-M212-RAM-2000kg/i-3521173
[180] Мировые рекорды в тяжёлой атлетике: https://ru.wikipedia.org/wiki/%D0%9C%D0%B8%D1%80%D0%BE%D0%B2%D1%8B%D0%B5_%D1%80%D0%B5%D0%BA%D0%BE%D1%80%D0%B4%D1%8B_%D0%B2_%D1%82%D1%8F%D0%B6%D1%91%D0%BB%D0%BE%D0%B9_%D0%B0%D1%82%D0%BB%D0%B5%D1%82%D0%B8%D0%BA%D0%B5
[600] Севморпуть, советское ледокольно-транспортное судно (лихтеровоз) с атомной силовой установкой: https://ru.wikipedia.org/wiki/Севморпуть_(лихтеровоз)
[610] Доска объявлений по продаже кораблей: http://www.seaboats.net
[620] Доска объявлений по продаже кораблей: http://www.vedshipping.com


Caracat
Муравей, как гугл подсказывает, способен поднимать и таскать груз весом в 50-100 раз более своего.
eugeneb0 Автор
Я бы с большим интересом ознакомился с какой-нибудь серьёзной работой, где это аккуратно измеряется. Всё, что мне удалось найти — это не очень внятные научно-популярные сайты. Где не проводится разницы между «тащить волоком» или «поднять», равно как «один раз в рывке» или «регулярно каждый день». А контроль этих параметров легко десятку раз дать может. По этой причине я не стал включать насекомых в анализ. Хотя и был соблазн.
Сам я, наблюдая за муравьями (могу видео поделиться), видел, что поднимают они соломинки размером примерно с себя, то есть и весом где-то такие же.
Но, как сказано, если есть работы, было бы интересно их изучить.
dedyshka
Journal of Biomechanics: The exoskeletal structure and tensile loading behavior of an ant neck joint.
eugeneb0 Автор
Из абстракта ясно, что мышцы шеи муравья способны выдерживать нагрузку до 5000-кратного веса муравья. Пожалуй, это действительно покруче, чем наши мышцы или стрела башенного крана. Явно Q >> 1 имеет место. Но не совсем понятно, как количественно это соотносится с долговременными нагрузками, регулярно выдерживаемыми муравьём в целом. Может, в полном тексте статьи это проясняется?
Moskus
5000 раз — это кратковременные нагрузки, например, при отрывании частей пищи или строительных материалов. Муравьи-листорезы, например, таскают куски листьев, которые предварительно отгрызает особый «отряд» рабочих, не сильно превосходящие их по весу, точно в пределах одного порядка. Иначе, им пришлось бы есть все время — эффективность химического топлива здесь тоже играет роль.
balexa
Да никак. Наши челюсти могут дать ~ 200 кг усилия при сжатии, а из детской книжки (Перельман по моему) я помню что бедренная кость способна выдержать вес груженого самосвала. И как это соотносится с нашими нагрузками? Правильно, никак.
Diordna
А я слышол около 1т
RiseOfDeath
Если про бедренную кость — мы в школе на физике считали — большая бедренная кость (сферическая в вакууме) выдерживает на сжатие до 5 тонн (по рассчету, исходя из ее сечения и табличных механических характеристик кости). Опять же это статичная нагрузка, т.к. когда вы тяжесть кладете, то онав момент «укладывания» окажет сильнее воздействие.
darthmaul
Масса и нагрузки растут кубически от размера, а прочность — квадратически. Поэтому детскую машину из пластика ребенок роняет с высоты в 10 её длин и она остается невредимой, а настоящий автомобиль из высокопрочной стали с высоты в 10 своих длин разобьётся всмятку.
sim31r
Настоящий автомобиль, за счет деформации кузова пытается спасти пассажиров и водителя, снижая ударные перегрузки. Аналогия верна, но автомобили делают, дополнительно, в разы более мягкими, чем могли бы обеспечить материалы.
У детского автомобиля еще и плотность ниже, и больше периметр на единицу веса, он вряд ли в свободном падении разгонится выше 50 км/ч, человек кстати стабилизируется на 200 км/ч в падении.
Чем меньше предмет, тем больше периметр, площадь, на единицу массы и медленней свободное падение из-за трения, это в дополнение к прочности.
gleb_kudr
Долговременно он тоже прекрасно все выдерживает. Объяснение простое — мощность мышц это квадратичная функция к линейным размерам (зависит от площади сечения), а вес — кубическая функция (зависит от объема). Точные значения там чуток другие, т.е. чуть меньше двойки и чуть меньше тройки. Но физический смысл остается тем же — при уменьшении линейных размеров относительная тяговооруженность мышц растет.
PS Прочитал дальше, ниже в каментах то же самое пишут.
DGN
Не очень быстро и не очень далеко. Потому и надо учитывать факторы скорости и расстояния. Что там у нас имеет самое низкое Q? Космические ракеты! Очень быстро и очень далеко! А что самое высокое Q? Конвейерная лента. Совсем медленно и недалеко, сравнимо с насовским тягачом, и по Q в том числе.
Кстати, не все эти транспортные средства тащат на себе свой источник энергии. По сути, это делает лишь ракета и атомный морской контейнеровоз. В некоторой мере, электротранспорт (он не возит с собой электростанцию, но и ракета не возит нефтеперерабатывающий завод).
eugeneb0 Автор
Конвейерная лента (равно как и парусник) отличаются по скорости от космической ракеты на три-четыре порядка. А Q почти одинаковые. Ну какая там может быть зависимость, о чем Вы? Максимум скромненький логарифм скорости с маленьким весом. Можете, конечно, попытаться его выжать из данных, я не против. Но почти уверен, что, кроме шума, там мало что выплывет.
DGN
Иными словами, скорость и дальность транспортного средства не зависит от его стоимости? Межзвездным полетам быть!?
eugeneb0 Автор
А вот не надо мне приписывать то, что не было сказано. Возникла гипотеза? Отлично. Посчитайте и результаты на стол. В цифрах и графиках. Тогда и поговорим. Предметно.
sim31r
Зависит, но минимум, как я понял при Q примерно около 1. Ракеты очень дорогие, но минимум цены при показанном авторе Q. Конвейерная лента дешевая, но еще ниже цена при указанном Q и нет особого смысла повышать её цену.
Mad__Max
Где же почти одинаковые если вы сами порядок разницы даже в среднем насчитали?
Это как раз самые далекие друг от друга категории.
Причем даже с учетом того, что ракеты вы судя по всему считали «сухими» — без запаса топлива, без которого они вообще ничего поднимать не смогут.
Иначе разница больше 2х порядков получилась бы.
eugeneb0 Автор
Уточните, не понял. Порядок разницы чего?
Mad__Max
Q различается на порядок (в ~10 раз)
eugeneb0 Автор
Вот график Q(v):

Зависимость Q от скорости по группам. Хорошо видно следующее:
1. Есть слабая зависимость от логарифма скорости.
2. Она статистически слаба (R2 = 0.47)
3.… и основывается, по сути, лишь на трёх группах. Из которых только одна (ракеты) представлена более чем одной точкой. Что, возможно, корректнее объясняется как «ракеты — особый случай», а не «общая зависимость».
eugeneb0 Автор
Вот график Q(v):

Зависимость Q от скорости по группам. Хорошо видно следующее:
1. Есть слабая зависимость от логарифма скорости. Как я и говорил.
2. Она статистически слаба (R2 = 0.47)
3.… и основывается, по сути, лишь на трёх группах. Из которых только одна (ракеты) представлена более чем одной точкой. Что, возможно, корректнее объясняется как «ракеты — особый случай», а не «общая зависимость».
Вопрос закрыт.
ZlobniyShurik
С муравьями и прочими насекомыми особой загадки нет.
Грубо говоря, усилие, развиваемое мышцами, прямо пропорционально поперечной площади сечения этих самых мышц (квадратичная зависимость от размеров). А масса груза, при прочих равных, зависит от линейного размера кубически.
Так что при уменьшении линейных размеров живого существа по всем измерениям (допустим, в 10 раз) получаем, что масса падает быстрее (1000 раз), нежели спадает усилие развиваемое мышцами (100 раз).
Отсюда и бешеная, по меркам среднего человека, относительная грузоподъемность насекомых.
eugeneb0 Автор
О! Вот это похоже на правду!
juray
Ну вообще, эффекты размерности с разной степенью функции — известная штука.
И в зоологии (например, для млекопитающих — замедление метаболизма и уменьшение потребления пищи с ростом размеров), и в технике — прочность сечения как квадратичная функция размеров vs масса как кубическая.
scifinder
Правильно ли я понимаю — тираннозавр ничего тяжелее ложки поднять не мог?
opckSheff
Вряд ли он мог поднять ложку. :)
ferosod
Скорее не мог поднять другого тираннозавра. Был бы еще больше — не смог бы и ложку поднять. Но не был бы, потому что эволюция.
dilukhin
Не знаю про тираннозавра, но слоны, говорят, прыгать не умеют. А киты и вовсе, лёжа на суше, даже дышать не могут толком. Теперь давайте сравним с блохой или кузнечиком.
u010602
Не умеют. Более того слоны меньше слоних не просто так, слониха не выдержит еще одну слониху у себя на крупе во время спаривания, а слона выдержит.
konst90
Больше. В полтора-два раза по массе.
u010602
Спасибо, всю жизнь думал иначе и в голову не приходило проверить. Увидел в детстве на дискавери.
LynXzp
У динозавров были свои фичи, например кости полые. Что не только уменьшало вес, но и позволяло прокачивать больше воздуха через легкие, используя полости как резервуар (как птицы делают сейчас).
Но все равно динозавры испытывали трудности из-за размеров своего тела.
mSnus
Сейчас люди тоже иногда испытывают, но мы стремимся к бодипозитиву!
oracle_and_delphi
У динозавров главной проблемой оказался не вес, а медленное размножение. В случае катаклизма — крысы и тараканы, размножаясь ударными темпами компенсируют любые потери, а динозаврам чтобы дорасти до полового созревания и приступить к размножению требовался не один десяток лет, что в условиях катаклизма слишком долго.
u010602
Прямо как люди в 21м веке. Еще меня пугает что раньше люди реагировали на любую проблему повышением рождаемости, а сейчас наоборот. Если мир стал хуже чем был, то многие люди отказываются от детей, мол зачем их мучать.
oracle_and_delphi
Про перенаселение никогда не слышали?
Когда реагировали на любую проблему повышением рождаемости в типичной семье был десяток голодных детей, из которых большая часть дохла не дожив до совершеннолетия, а более половины взрослых дохло не дожив до старости в результате очередной войны (и даже, не в качестве солдат, а в процессе грабежа учинённого бандами мародёров).
u010602
Плотность населения в Индии выше чем раньше, и рождаемость не падает. Плотность населения в странах СНГ ниже и рождаемость падает. Я не думаю что перенаселенность влияет на рождаемость. Я думаю влияет осознанность этого процесса, раньше рожали и не переживали за судьбу ребенка. А сейчас переживают, и если не уверены что могут или хотят обеспечить ребенку жить выше среднего — отказываются.
oracle_and_delphi
В Индии рождаемость к середине 2010-х вообще-то уже упала.
u010602
И тем не менее она выше, чем в СНГ, Китае и США. Она упала по той-же причине что и везде — рост обеспеченности и осознанности.
Glays
Не пугайтесь, почитайте про демографический переход
u010602
Почитал, там нет ни каких положительных прогнозов. Лишь анализ причин происходящего.
Glays
Вы пишете
Но там говорится что люди отказываются от детей именно из-за того что мир стал лучше.
Прогнозы там тоже есть и повышенная рождаемость в них как раз противоречит позитивным тенденциям.
u010602
Еще раз перечитал и не нашел таких прогнозов. Можно цитату пожалуйста. А то я вижу это
Я это писал в контексте реакции на негативные факторы. Например в Украине в 2014 когда началась война, я слышал частые изречения «куда рожать, ужас же!».
Glays
Ну и кому поможет увеличение рождаемости, которое приведёт к перенаселению и в следствии резкому спаду уровня жизни человечества, глобальному голоду и социальным катаклизмам?
Кому поможет увеличение рождаемости во время резкого спада уровня жизни человечества, глобального голода и социальных катаклизмом вызванных перенаселением?
u010602
Меня больше заботит в этом процессе не спад уровня жизни, а выживаемость моих генов после спада. На данном этапе идет гонка, кто какую долю займет в этих 12 млрд. П.С. уровень жизни меня вовсе не беспокоит, есть своя романтика жить натуральным хозяйством например.
a5b
https://en.wikipedia.org/wiki/Square%E2%80%93cube_law (Закон квадрата — куба,… first described in 1638 by Galileo Galilei in his Two New Sciences as the "...ratio of two volumes is greater than the ratio of their surfaces")
Weerel
Нет. Мощность все-таки пропорциональна всей мышечной массе. Соответственно тоже кубу линейных размеров. Для отдельной мышцы пропорциональна ее массе, а не сечению. Если мышца тонкая и длинная, имеет смысл говорить об удельной мощности на единицу длины. Допустим есть груз, который должны сдвинуть два трактора. Как их запрячь, последовательно или параллельно, не так важно. В любом случае справятся с задачей и разовьют сопоставимую мощность. Работа мышцы — это сила на перемещение. Сила действительно зависит только от сечения, а вот перемещение как раз пропорционально длине. Каждый кусочек немного сжимается и совершает часть своей работы, приходящейся на всю мышцу.
Тем не менее фактор масштаба присутствует. Все дело в метаболизме. Чем меньше организм, тем выше метаболизм. В том числе мощность на единицу мышечной массы. Самое простое объяснение, что теплообмен с окружающей средой пропорционален поверхности. А тепловыделение — массе. Поэтому для поддержания постоянной температуры (для теплокровных) — метаболизм должен быть обратно пропорционален линейным размерам. От масштаба зависит и опорно двигательный аппарат. Для небольших размеров нет никаких ограничений, чтобы обеспечивать большую удельную можность. Для больших размеров он банально не сможет выдержать нагрузок, котрые в состоянии создать мышцы. Или если все таки сможет, то это должна быть сложная и дорогая конструкция. Вот тут как раз прочность костей определяется их сечением, а нагрузки всей мышечной массой.
sim31r
Вроде проблем с перегревом нет особых. Самые крупные животные как-раз в Африке живут. На севере средних размеров, хотя на севере большие размеры выгоднее для сохранения тепла.
VolCh
Два из трёх подвидов самого крупного животного на настоящий момент и, вероятно, самого крупного существовавшего на Земле когда-либо, тяготеют к холодным кругополярным водам.
sim31r
По какой причине? Может больше корма в воде? Планктон для китов, например.
По моим наблюдениям, в холодных водах даже крупные животные много ресурсов тратят на сохранение тепла, шерсть, толстый слой жира. Даже в теплом климате у большинства животных достаточно теплая шерсть. Что свидетельствует о проблеме переохлаждения, а не перегрева.
Перегрев, вероятно, был бы актуален животным на порядок больших размеров, чем существующие, весом в 500 тонн и более. Но нужно моделировать.
Даже у кита весом в 100 тонн, есть защита от переохлаждения, ну и запас на случай голода
jrthwk
… поэтому 50 грамм муравьев могут сбегать за бутылкой пива. (с)баш
evgusihin
Нужно еще бурлаков на Волге оценить
u010602
Думал над графиком легковых авто. И авто «чтоб ехать» за 100к. Я думаю это дешевые авто переходящие в спортивные купе. Не думали взять именно спорт кары, масл кары и пикапы(типа сильверадо) для анализа и коммерческие легковушки.
eugeneb0 Автор
Скорее всего Вы правы. Думал провести отдельный анализ, но сил и времени просто не хватило. Может, кто из читателей удосужится.
DGN
Трубопроводный транспорт не посчитали?
Электросамокат?
Логично как то увязать не только отношение транспортного средства к массе груза, но и время с расстоянием (иначе, как считать к примеру конвейерную ленту и трубопровод, железную дорогу).
u010602
Я по ленте вообще не согласен. Лента сама себя не питает, и лента сама себя не движет. Отсюда и дополнительная масса, которую она может перевезти.
DGN
Сова вообще трещит по всем швам. Если поезд с рельсами, то почему атомный контейнеровоз без океана?
u010602
Я думаю логично взять не весь океан, а воду, которая обеспечивает плавучесть.
DGN
Как будто бы у нас от старта до финиша есть канал нужной глубины-ширины или просто по водоизмещению судна?
eugeneb0 Автор
Ezhyg
Архимед только что в ванной поскользнулся. Термин «водоизмещение» прошёл мимо?
Кстати, в тему про воду — как насчёт буксиров и несамоходных барж?
Или пары мелких буксирчиков, толкающих огромный сухогруз?
Или тягач везущий на себе груз (максимально облегчённый, потому что использует вес перевозимого).
eugeneb0 Автор
А что не так с водоизмещением?
Вот корабль с грузом массы m. На него сверху вниз действует сила тяжести mg. Снизу вверх на него действует сила Архимеда F. Поскольку корабль не улетает ни вверх, ни вниз, mg = F. Далее, чему равна F? F = ?gV, где V — объём погружённой под воду части. Поскольку вода (в первом приближении) несжимаема, этот объём, втиснутый в воду, и есть объем воды, которая вытеснилась (предполагая сосуд изначально полным). Сокращая g, получаем m = ?V. Правая часть есть масса вытесненной воды. Она равна, как видим, массе корабля. ЧТД.
Буксиры и баржи — надо посчитать. Баржа ведь тоже что-то весит. Q, наверное, получится побольше единички, но вряд ли уж за десятку.
adictive_max
Да даже если и большое получится, то ничего удивительного. Из графиков хорошо видно, что Q заметно больше 1 очень дорого даётся. Конкретно с буксиром это даётся ценой очень маленькой скорости и около-нулевой маневренности.
nvor
Ценой скорости. Из вики: От других судов буксиры отличает высокая удельная мощность, хорошая маневренность, повышенная прочность корпуса и остойчивость.
adictive_max
Это маневренность самого буксира. А маневренность сухогруза, толкаемого буксиром, примерно никакая, но для мелких перемещений хватает.
Ezhyg
С водоизмещением всё так, но только у подводной лодки весь объём полностью погружается под воду, у нормальных же кораблей есть подводная и надводная части, которая, вместе с большой частью груза, если говорить о сухогрузах — над водой и она не вытесняет «объём» воды равный по массе… и далее по тексту Архимеда. То есть корабль (судно) погружённой частью вытесняет воды «с запасом» ещё и на надводную часть и на груз. То есть, корабль (его подводную часть), по определению, приходится делать более «водоизмещающим», там же нужна не нулевая плавучесть. То есть, по определению — больше единицы.
Мало того, если не путаю, у них есть заполняемые водой отсеки, почти как у подводной лодки, чтобы осадку дать для устойчивости (кажется остойчивость называется) пустого кораблика и при погрузке они постепенно «продуваются», вроде.
В общем, как это вижу я, простая физика подаётся, как некое «открытие». Хотя такое я уже не первый раз наблюдаю — что я сам ребёнком читал в журнале ЮТ в 80-ых годах, сегодня подаётся как открытие года (это не к вам, а вообще). И это не абстрактный пример, именно такое вот «переоткрытие» информации из статьей ЮТ я сам, прямо здесь, видел минимум 5 раз и даже хотел написать об этом… но не с моими писательскими способностями. :(
aleksandros
Автор всё правильно написал. Корабль вытесняет такую массу воды, сколько весит сам, ни больше, ни меньше. Эта характеристика и называется водоизмещением. А объём этой воды равен объёму погруженной части корабля. Соответственно, верхняя, надводная, находится над водой.
Другими словам, «средняя плотность» корабля меньше плотности воды. Именно по этому он и не тонет.
Ezhyg
Так я это же и пояснил, нет?
Mad__Max
Нет, пытались невнятно «доказать» свое исходное ошибочное утверждение, что масса вытесненной кораблем воды якобы не равна массе этого самого корабля.
Ezhyg
Вообще-то это был саркастичный комментарий, похоже, не слишком удачный, с намёком, что «всё это» называется одним словом.
avost
Вы, наверное, удивитесь, но это не имеет значения. Что подводная, что надводная часть корабля вытесняют объем воды равный по массе… и далее по тексту Архимеда.
Нет, конечно. При недогрузе судно "всплывает" и вытесняет меньший объём воды. "чудесным" образом в точности равный его текущей массе.
Возможно, у каких-то судов такое есть, но, как правило, нет. В любом случае это не имеет значения в контексте обсуждаемой проблемы.
Да, да. Старая байка о том, что японцы якобы сделали квадриллион бабла, патентуя заметки из ют и науки и жизни.
Ezhyg
Вы удивитесь, но вы не читали комментируемый коментарий, ладно, согласен пойти на уступку — читали невнимательно.
Надводная часть ничего не вытесняет, потому что… она надводная! Удивительно, не так ли? И поэтому за неё приходится отдуваться подводной :D
И снова вы подтверждаете, что читали невнимательно. Весь корабль — весит больше, чем только подводная часть, а надводная не вытесняет ничего, по причине названной уже три раза и поэтому подводную часть приходится делать большего объёма.
Он перевернётся и утонет и никуда больше не поплывёт — очень даже имеет :P.
Заметьте, про японцев не я заговорил. Вообще-то я говорил, что прямо здесь, на этом сайте такое появлялось и это были не только переводы.
VolCh
Надводная часть вытесняет путем передачи своего веса подводной, а подводная непосредственно за себя и за вес надводной. Уберите надводную часть и часть подводной станет надводной.
eugeneb0 Автор
Если представить себе корабль в очень тесном облегающем шлюзе, то воды там вообще капля. Считай ноль массы.
Так что не очень понятно, сколько же воды «обеспечивает плавучесть», и весь наш спор, пожалуй, бессмысленен.
u010602
Не совсем понимаю, почему в очень тесном шлюзе корабль будет плавать как-то иначе. Если корабль в шлюзе стоит на дне — то он плавать не может, он уже не ТС. Как машина без колес — легче но не ездит. Корабль который плывет всегда требует воды той-же массы что и сам.
YMA
«Вытесненной» воды, т.е. виртуальной. Если пытаться умозрительно поднять вверх корабль из такого шлюза «в обтяжку» — сразу это поймёте.
По водному транспорту вообще интересно. Берем вырожденный, но реальный случай — плот из стволов деревьев, сплавляемый по реке. Масса «груза» — сотни тонн, «сухая масса» — около нуля (плотовщики с шестами, но даже если добавим двигатели для маневров, Q все равно заоблачный будет.)
u010602
Если в вашем шлюзе-презервативе воды меньше чем масса корабля — то корабль просто сядет на дно, а вода будет стоять где-то там вверху. Вы ни когда реально (а не умозрительно) не вставляли кастрюлю в кастрюлю? Законы физики топологией не обмануть.
YMA
Посмотрите описание опыта №2 тут www.rusnauka.com/27_NNM_2011/Phisica/2_92717.doc.htm
А там я доберусь до дома, возьму два пластиковых стаканчика разных размеров, пластилин и воспроизведу опыт вживую ;)
u010602
в первом же абзаце ошибка
А вот верная формулировка.
Даже не знаю стоит ли дальше читать после этого… Буду ждать вашего воспроизведения опыта
YMA
Стоит, узнаете немного про физику ;)


Итого, нашел два стаканчика и воду. Как видно на первом фото — стаканчик с гирькой 100 гр. и магнитными шариками весом 50 гр. плавает (именно плавает, можно утопить и глубже, или покрутить) в другом стакане, в котором содержится 64 гр. воды. Фото на весах тоже есть, но тут и на глаз видно вес объектов.
u010602
Вы правы, эффект называется Гидростатический парадокс
avost
Ну, вы, блин, даёте! Нет, конечно. Архимедова сила не зависит от фактического объёма воды, а только от объёма погружёного тела. Архимедова формулировка просто численно приравнивает этот объём к объёму фактически вытесненной воды. Попробуйте вывести архимедову силу, интегрируя гидростатическое давление по поверхности погружённого тела. Для простоты представьте кубик, погружённый в жидкость так, чтобы одна (обе-две) грани были горизонтальными. Вы же не будете спорить, что архимедова сила будет равна интегралу по поверхности нижней грани от давления (боковые силы давления будут скомпенсированы)? А этот интеграл численно равен площади грани, умноженной на глубину погружения грани и умноженной на плотность воды (следует из определения поверхностного интеграла и закона Паскаля). И ни какой объём воды тут не будет фигурировать вообще. Так понятнее? Поэтому корабль в доке-презервативе таки будет плавать (если, конечно, обеспечить какое-то пространство для воды по всей погружаемой поверхности).
Насчёт кастрюль, не знаю уж что вы с ними такого проделывали, а я такое делал неоднократно, собирая из подручных средств водяную баню. Всё прекрасно работает, как и полагается по законам физики.
u010602
А чем обеспечивается по вашему давление жидкости на дно кубика? Насколько я знаю, оно обеспечивается массой жидкости выше дна. Когда у нас большой резервуар, типа океана, мы можем в первом приближении рассчитывать просто высоту водного столба. Но когда количество свободной воды значительмо меньше обьема тела — то это уже не работает. Фактически мы имеем тут систему из двух сосудов. В одном поршне наш кубик подперт снизу водой. В другом сосуде мы имеем свободную воду. Отношение площадей двух цилиндров будет влиять на отношение разницы уровне в сосудах. Так вот что-бы фактически поднять кубик со дна его сосуда, нужно будет в другой сосуд налить воды по массе как этот кубик. А иначе кубик просто будет стоять на дне. Это как весы по сути аптечные. Хз как еще это объяснить.
u010602
Вы правы, эффект называется Гидростатический парадокс.
juray
Он самый. Хотел было накатать аргументов к вашему комменту выше, но заметил эту корректировку.


Но картинок подкину:
Virgo_Style
Плоты, imho, это читерство. Если рассматривать объекты, движущиеся под действием внешних сил, то можно вообще прийти к грузу, который космонавт Иванов бросил космонавту Петрову в невесомости космической станции. Иванов — внешняя сила, упаковки у груза нет, Q равно бесконечности.
u010602
Иванов просто реализует потенциальную энергию груза. Так считать не верно, т.к. запасалась эта энергию двигателем ракеты.
С плотами опять-же ни какого читерства не вижу. Плот он же груз, он же корабль. Он сам себя везет за счет внешних сил. Q равен 1 если нет плотовщика, и чуть менее 1 если есть. И то только благодаря наличию течения реки. Без течения будет Q=0. В данном случае течение реки это внешний источник энергии. И я считаю автору не стоило включать такие устройства в анализ. Например у конвейерной ленты так-же источник энергии не учтен и как результат не адекватное Q.
Virgo_Style
По-видимому, я как-то криво сформулировал свою мысль, ибо имел в виду ровно то же самое %)
А вот насчет потенциальной энергии, честно говоря, не понял. Иванов же не роняет груз на матушку-Землю, а тот не падает на нее. Орбита, невесомость, груз летит-плывет из т.И на расстоянии N от Земли в т.П на том же расстоянии N (для простоты) от Земли.
Да и странно как-то, что наши рассуждения начинают зависеть от происхождения груза.
u010602
На рассуждения зависят не от происхождения груза, а от происхождения энергии, которую груз тратит на перемещение в пространстве. Если вы про обмен грузами между двумя станциями на орбите. То там мы вообще груз не двигаем, мы его бросаем и ловим. Не думаю что это относится к транспортным средствам в принципе. Мы ведь не преодолеваем сопротивление ни каких сред. Так можно и движение электрона записать в анализ.
eugeneb0 Автор
— Пожалуй. Но лента там — одна точка, картину в целом не делает.
eugeneb0 Автор
— Увяжите. С интересом гляну на результат.
wapuku
А как-же всевозможные роботы-«домкраты», как на складах Амазона?
eugeneb0 Автор
А что по ним? Я не в курсе.
robert_ayrapetyan
Ну вот электросамокат, 25 кг с батареей. Способен везти 100 кг (т.е. это Q = 4.0 по вашим определениям). Но не очень быстро. И не долго. И не в крутую горку. Без всех этих уточняющих параметров смысл Q как-то ускользает.
eugeneb0 Автор
Электросамокат ездит без человека?
DGN
В той же мере, как и грузовик.
Updated
С другой стороны, вес человека как управляющего элемента грузовика почти не сказывается на его массе. А если взять большой электросамокат, весом 30кг и способный везти двоих, то есть 75+75кг, получаем Q=1.4 — бинго! Сова снова на глобусе.
YMA
На электросамокате весом 10 кг едет сын весом 25 кг и везёт меня весом 100 кг — Q=3, глобус на сове ;)
pulsatrix
Оставтье уже сову в покое
robert_ayrapetyan
Не очень понимаю к чему вы клоните. Человека к грузу нельзя приравнять или что?
eugeneb0 Автор
В общем, там выше мою мысль уже поняли и пояснили. Нельзя приравнять. Человек в самокате выполняет стуктурную и балансирующую роль. Без него (в отличие от груза) самокат никуда не поедет.
Если только Вы не имели в виду какой-нибудь самоуправляемый самокат, я почему и задал уточняющий вопрос.
Kroid
Оторвите ручку, чтобы осталась только платформа. Добавьте еще два колеса, чтобы она была устойчивая. Прикрутите какую-нибудь ардуино, чтобы автономно ездить.
Получатся вот такие «электросамокаты»:
www.youtube.com/watch?v=H5pChlqcm40
Интересно, какое у них Q.
eugeneb0 Автор
ТТХ на видео не вижу, но по размерам не удивлюсь, если с восьмёрку.
Впрочем, я начинаю подозревать, что на массах ниже 100 кг закономерность Q ? 1 начинает таки ломаться. Там выше в обсуждении про муравья народ интересные мысли на эту тему высказывал.
Opaspap
Ну какой самокат, мотобайк 125cc (а то и 110) может везти водителя, его друга и два других мотобайка на багажнике одновременно, не знаю как по расчетам, но я каждый день подобную магию вижу, как еду на работу. Вес такого транспорта 80-120kg бензина в баке 3-4 литра.
gleb_kudr
25 кг самокат способен везти и быстро и долго :) Там необходимого железа килограмм на 12, остальное можно занять батарейкой.
justserega
После прочтения сложилось впечатление, что вы подгоняете данные под гипотезу. В случае с грузовиком вы берете максимальную полезную нагрузку единицы техники, а в случае с ракетами — рассматриваете только тягу двигателя. В случае с ракетами полезную нагрузку нужно не просто переместить, а разогнать до какой-то скорости (ее максимальный вес прямо зависит от того до какой скорости нужно разогнать).
В пользу этого предположения говорит, что вы пытаетесь добавить к массе поезда рельсы, к контейнеровозу воду, а к самокату вес водителя. Это все очень явные манипуляции, поставьте четкое определение, что такое «полезная нагрузка» и что «сухая масса» (почему кстати сухая, без топлива ничто не поедет).
eugeneb0 Автор
Знаете, я тут немного занят, а комментаторов много. Можно, я кратко?
К контейнеровозу воду в расчётах я не добавляю. Это кого-то из комментаторов идея.
Без топлива ничто не едет, но уже с 10% топлива едет всё. А вот без человека самокат вообще не поедет. Никуда. Как и телега без лошади. И 10% человека в систему не посадишь.
За исключением ракет, масса топлива, даже если её включить в картину, выводов радикально не меняет.
Топливо структурной нагрузки (почти) не несёт.
Картина вообще чрезвычайно устойчива к упомянутым Вами неоднозначностям. Я, скажем, долго думал, включать ли массу рельсов. Решил — так точнее. Но можно и наоборот. От этого мало что меняется. Точек-то сотни. Я для чего и выложил данные. Чтобы, если кто сомневается или хочет посчитать лучше, могли бы. Пусть люди пробуют, проверяют. Но мне думается, основные выводы останутся те же.
Справедливо, что масса ПН конкретной ракеты зависит от конечной скорости. Но ведь конкретная ракета (космическая ли, баллистическая или там противотанковая) уже конструируется под фиксированную конечную скорость. Никому не нужен «космический» носитель, поднимающий 50% своего веса — но только до ближайшего океана. И все хотят, чтобы эта ПН была не слишком мала. Так скорость и пропадает из картины.
Не очень понял комментарий про нагрузку единицы техники vs тягу двигателя, не поясните?
vanxant
Забавно, но ракетное топливо можно и посчитать:) Но без окислителя, так как все прочие там грузовики, кроме электро, берут кислород «бесплатно» из воздуха. Окислителя в ракете примерно 2/3 стартовой массы.
mSnus
Телега не везёт лошадь.
А самокат везёт человека.
Germanjon
Кстати, да. Соответственно, нужно оценивать грузоподъёмность самоката, которого за руль везёт человек, идущий рядом
VolCh
Самокат, велосипед, мотоцикл и т. п. в общем случае пассажирское транспортное средство, а не грузовое. А если грузовое, то водитель становится принадлежностью самоката.
vvzvlad
Человек, в общем-то, там только равновесие держит. Думаю, в 7кг(10% от человека) уложится масса гироскопа, который будучи раскрученным, будет так же держать равновесие. Тем более, активно его держать надо только на старте.
eugeneb0 Автор
Плюс какие-то решётки прочности. Чтобы 100-килограммовый груз не вываливался на старте или повороте. Ну, получится Q в районе тройки, возможно.
vvzvlad
Ну, на самом деле, я не прав. Человек там — еще навигация.
konst90
Нет.
Машина с 10% топлива перевезет груз на 10% расстояния. Ракета с 10% топлива поднимется километров на двадцать и шлепется неподалеку от места старта.Атомоход с 10% стержней в реакторе вообще из порта не выйдет, думаю. Конвейерная лента… а что вообще для неё топливо? Как и для электровоза, кстати.
Поэтому топливо учитывать надо, без него никак. Более того, оно ещё и разную относительную массу имеет — на порядок. В машине это 2-5% от полной массы (т.е. от того, что мы имеем на старте), у ракеты — примерно 90%. Или даже так — в машине это 10% от массы груза, в ракете — 1000%.
А потом ещё и скорость/расстояние учесть…
eugeneb0 Автор
Вы кое-что упускаете.
Вот грузовик полностью заправлен. Он тащит 5 тонн груза. Его конструкция воспринимает определённую нагрузку. Он долго ехал в свой пункт Б и под конец в баке осталось 10% топлива. Но он по-прежнему тащит 5 тонн груза, нагрузка на конструкцию осталась одна и та же. Инженерная сложность, потребная на создание этой конструкции, не зависит от того, сколько топлива осталась в баке. А мы интересуемся измерить именно как стоимость конструкции зависит от этой инженерной сложности, задаваемой массой. Топливо в этой картине ни при чём абсолютно.
Равно как и с ракетой. Перед отключением первой ступени в баках топлива вообще 3% может быть. Но конструкция работает так же, и сложность её от выгорания топлива не меняется.
Если Вы начнёте считать с топливом, вы смешаете две очень разные вещи: цену разработки прочного корпуса, и (почти нулевую) стоимость топлива, нагрузки не несущего.
VolCh
В случае ракеты прочный корпус потому и нужен, что топливо и окислитель тяжелые. Если обеспечить внешний их подвод (шлангами какими-нибудь, или разгонного вертикального «рельса»), то вес ракеты будет на порядки меньше.
vvzvlad
Тут вопрос вот еще в чем: любое средство передвижения должно выполнить свою функцию, иначе оно не очень средство. Грузовик должен отвезти тонну картошки в магазин, ракета — спутник на орбиту. Очевидно, что сломанный грузовик(или часто ломающийся, каждый километр, например), эту функцию выполнять не может — он или не едет, либо его эксплуатация требует второй машины с механиками, и ну его нафиг. И в этом случае, действительно, работа грузовика в первом приближении не зависит от количества топлива в его баке — было бы можно доехать до заправки: если сделать бак размером 10% от стандартного, эксплуатировать грузовик будет как минимум возможно. Вот на 1% размера бака — уже скорее всего нет, а на 10% да.
С ракетой ситуация иная: ни с каким уровнем топлива, кроме как со 100%(опустим пока запас) она спутник на орбиту не доставит — или упадет, недолетев, или выйдет на нерасчетную орбиту. Соответственно, грузовик, заправленный на старте 10% топлива, функционировать может, так как именно с таким обьемом топлива его работа становится, в некотором роде, самоподдерживающейся — заправиться, чтобы доехать до следующей заправки, где заправиться, чтобы… и так далее. Ракету надо обязательно заправлять на 100%.
Соответственно, именно с таким количеством топлива надо считать массу для вычисления Q — некий процент заполненности бака(исходя из среднего расстояния между заправками и потребления топлива) для машины, и полная масса топлива для ракеты.
sim31r
С ракетой всё сложнее. Топливо и есть основной её вес. При стартовой массе в 10% она стартанет с ускорением в 10G или выше (вместо запланированных 1.4) и быстро наберет большую скорость. Там нелинейная зависимость. Топливо не только перемещает ракету, но и является балластом. Остаток топлива самое ценное.
А если загрузить топливом на 200%, то может висеть с нулевым ускорением, пока не сожжет излишек топлива, не позволяющее оторваться от Земли ))
vanxant
висеть на опорах…
justserega
> Никому не нужен «космический» носитель, поднимающий 50% своего веса — но только до ближайшего океана.
Тогда почему рассуждения в статье идут про первую ступень без топлива? Давайте на примере Falcon 9 FT (расчеты грубые, но чтобы показать идею сойдет)
Стартовая масса: 549 т.
Полезная нагрузка (НОО): 22.8 т. (Q = 0.0415)
Полезная нагрузка (ГПО): 5.3 т. (Q = 0.009)
Марс: 4 т. (Q = 0.07)
Из этого видно, что для ракет вес полезной нагрузки зависит от того куда конкретно нужно ее забросить. С одной стороны найденная вами линейная зависимость массы техники от массы полезной нагрузки ожидаема, но с другой вольность трактовок позволяет делать громкие заявления, что они 1:1.
И еще важный момент — грузоподъемность это важная величина для грузоперевозок, но зачем тогда сюда пытаться притянуть легковой и спортивный транспорт у которого полезная нагрузка может быть далеко не первым параметром оптимизации.
VolCh
С рельсами с одной стороны точнее, но с другой их крайне редко прокладывают под одно ТС (в голову приходят только узкоколейки очень местного масштаба и рельсы башенных кранов), а длина очень различаться может. То есть в формулу нужно вводить ещё и длину перемещения, размерность Q должна быть не безразмерная, а 1/км
justhabrauser
«Подгоняете данные под гипотезу» — ну да, без учета эффективности, целей и т.п.
Особенно умилила экстраполяция графиков (где точки разбросаны плюс-минус лапоть) и ведро допущений из пальца.
Ловкость рук — и никакого мошенства (tm).
Я так тоже умею:
* температура по больнице в среднем — 36.6
* вероятность встретить динозавра на улице — 50%
Ну и т.д.
NP447
Встречал в сети похожее исследование с соотношением максимальной скорости ТС и произведения удельной силы тяги на максимальную скорость:

alex-anpilogov.livejournal.com/72668.html
Результаты точно также лежат на одной прямой в логарифмических координатах.
catharsis
Потому что более мощный транспорт обычно едет быстрее, иначе зачем его делать мощным.
Сопротивление среды в общем случае зависит от квадрата скорости, то квадрат скорости примерно пропорционален тяговооруженности, то есть P/(mgv^2) ~= const, что показывает этот график.
На самом деле, бурный прогресс пароходов, который дал нам "Титаник", опирался на масштабный эффект: сопротивление и потребная мощность двигателя растет скорее с квадратом линейного размера, а полная масса и запас топлива с кубом, то есть в 64 раза более тяжелый пароход при прочих равных сможет уплыть вчетверо дальше, но на этой диаграмме будет вчетверо хуже из-за низкой тяговооруженности.
phenik
Спасибо, очень интересное исследование) Вы рассматриваете зависимость цены от условной эффективности машин. Есть еще одна интересная зависимость — времени эксплуатации (средней, максимальной) от удельной мощности. Чем она интересна? Тем, что по смыслу напоминает зависимость макс. продолжительности жизни особей биологических видов от удельного значения основного обмена, кот. для живых систем можно считать удельной мощностью, необходимой для поддержания жизнедеятельности в условиях покоя. Эта эмпирическая зависимость в свое время дала основания для предположений о зависимости макс. прод. жизни особей видов от интенсивности метаболизма, и механизме старения, как накопления нарушений в организме, связанном с окислительным стрессом (условно «горением», сопровождаемого тепловыделением). Есть много вариантов объяснения этого механизма, наиболее продвинутым из которых является теория митохондриальная свободнорадикальная теория старения. Вот график такой зависимости по данным из базы AnAge, для млекопитающих, для кот. имеется информация о величине осн. метаболизма: Интуитивно понятно, что чем больше удельная мощность машины, тем интенсивнее ее износ связанный с эксплуатацией. Возникает вопрос есть ли аналогичная степенная зависимость для машин, и др. технич. систем, например, для процессоров. В одном из коментов пытался сделать такую оценку для автомобилей:
Интуитивно понятно, что чем больше удельная мощность машины, тем интенсивнее ее износ связанный с эксплуатацией. Возникает вопрос есть ли аналогичная степенная зависимость для машин, и др. технич. систем, например, для процессоров. В одном из коментов пытался сделать такую оценку для автомобилей:
«Конечно машины мало напоминают организмы, в основном по тому, что они не обладают свойством роста и самовосстановления. Но все же они периодически восстанавливаются во время техобслуживания и ремонтов, хотя и с помощью людей. И еще, машины можно по аналогии с животными классифицировать, разделяя на семейства. К примеру, если упрощенно, гоночные болиды, легковые и грузовые авто, с соотв. параметрами средних мощностей, масс и времени эксплуатации. Можно также ввести аналог инт. метаболизма, если отнести мощность к массе. Макс. время эксплуатации не найти, потому взяты некоторые предельные по нормативам из сети. Для болидов срок не нашел, но двигатели F1 расчитаны на ~2000 км пробега. Посему сред. срок эксплуатации можно определить в несколько лет, для определенности возьмем 3. Получается такая «удельная инт. метаболизма» и «МПЖ» для машин: для болидов ~ 700/1000 = 0.7 и 3 года, для лег. машин ~ 150/1500 = 0.1 и 12 лет, для грузовых ~ 400/6000 = 0.07 и 20 лет. Если построить график, то он тоже будет аппроксимироваться степенной зависимостью, особенно, если брать множество конкретных марок машин. Какие семейства млекопитающих условно могут соответствовать этим авто-семействам? Гоночным болидам — землеройковые, чемпионы по инт. метаболизма среди млекопитающих, и имеющих самую короткую МПЖ (на графике представитель семейства — Белобрюхая белозубка). Легковым авто — к примеру, семейство землекоповых (на графике — Дамарский пескорой), а грузовым — медвежьи (на графике — Медведь губач).»
Конечно, как и у каждого отдельного человека, или особей др. видов со своей индивидуальной историей жизни, у каждой машины своя индивидуальная история эксплуатации. Но тепловыделение связанное с расходом энергии для выполнения функций является одним из основных факторов их повреждения и износа, и влияет на время «жизни», как биологических организмов, так и машин, и связано с физическими ограничениями.
eugeneb0 Автор
Интересно, спасибо!
Germanjon
Идея хорошие, результаты интересные, но много вопросов к чистоте экспериментов:
Ограничения на тип транспортного средства: нужно указать требования, что и как оценивать, в каких условиях. Например, шагающий экскаватор (1000 тонн) тоже служит для перемещения груза в ковше/дреглайне (30 тонн) с существенно низким Q. С другой стороны, канатом (масса 50 кг) можно тянуть на тележке массу в десятки тонн. Целлофановая плёнка (масса менее 1 кг), надутая воздухом, перемещала нескольких ребятишек (совокупная масса около 100 кг) на практически любое расстояние вниз по течению реки. Целлофановая плёнка (масса менее 1 кг) перемещает нескольких взрослых (совокупная масса более 200 кг) вниз со снежного склона.
Ограничения на условия эксперимента: трудно сравнить «мягкое с тёплым». Для каждого технического средства есть наиболее выгодные условия применения. Пытаться вывести «среднее по больнице» приведёт к погрешностям измерений, либо к намеренному ограничению выборки (чтобы она соответствовала условиям).
Путаница с тем, что включать или не включать в состав ТС: В каких-то случаях топливо играет неотъемлемую часть ТС. В каких-то случаях водитель или лошадь является неотъемлемой частью… Как понять, когда это происходит? Может быть поставить условие, например транспортное средство должно переместить груз в своей привычной среде (дороги, воздух, космос, вода) при наличии благоприятных условий (штиль, попутный ветер, идеальное дорожное покрытие) на определённое расстояние (N километров, M корпусов транспортного средства), за время, не превышающее X единиц, при условии нулевой начальной скорости.
eugeneb0 Автор
Да, пожалуй, есть над чем подумать. Спасибо за мысли!
Afterk
Сравнивать машины с самолётами и ракетами это уже слишком, назначения совсем разные. Вот curb weight типичной машины:

Сразу видно что если заменить сталь/чугун на что-то очень легкое, то можно существенно уменшить этот вес. Но при этом новый материал должен соответствовать инженерным, технологическим и экономическим требованиям.
vvzvlad
Так прикол-то в том, что никто не заменяет: невыгодно.
eugeneb0 Автор
Заменить можно. Но ведь дороже получится.
vanxant
Ну вот болиды формулы-1 — в них именно что заменяют сталь на «что-то очень легкое» в пределах техрегламента (ну, чтобы от столкновения с травинкой не развалился). Было бы интересно посчитать Q для этого случая. Но думается, там тоже не больше 10-20.
vvzvlad
А возит он человека массой в 100кг, и все.
Caracat
У автомобиля из-за различных передаточных чисел коробки передач будет разное Q. Причем на низших может тягать кого-то еще, а на высших и себя сдвинуть с места не сможет. Но начав с грузом движение с низшей передачи, разгоняясь по хорошей дороге, переключаясь на высшие, может очень быстро ехать, расходуя меньше топлива, чем на старте. Силы инерции и накат на хорошей дороге тут в помощь. Как тут Q считать?
eugeneb0 Автор
Я подходил к вопросу просто. В справочнике написано «4 тонны»? Значит, люди, которые грузовик делали (и которые лучше меня в нём разбираются), уже учли особенности коробки передач и составили картину типичных условий эксплуатации. Для которых получается 4 тонны и такое-то Q.
Разумеется, опытный водитель (равно как, кстати, и правильное распределение груза) этот справочный предел превысить может. Но… опытный водитель дополнительных денег стоит ))
sim31r
Зачем на высших передачах трогаться с места? Передачи для экономии топлива, чтобы поддерживать обороты двигателя в оптимальном режиме, это особенность (недостаток) двигателя внутреннего сгорания. У электромобилей вообще нет коробки передач, электромоторы тянут на одной передаточной скорости нормально.
Да, потому что Q примерно около 1, грузовик массой 10 тонн может тягать груз 10 тонн или другой грузовик массой 10 тонн. Противоречия нет.
vanxant
Нет, там стоит хитромудрый контроллер, который раздает токи-напряжения-частоты в зависимости от оборотов.
Есть универсальное правило, следующее из законов сохранения энергии и импульса. Для линейного движения (ракет) оно звучит как P = T * u, где P — полезная мощность двигателя, T — тяга, u — скорость истечения (газа из сопла). Для кругового вращения (двигатели наземных транспортных средств) там вместо T и u будет крутящий момент и скорость вращения вала. Коробка передач при помощи шестерней позволяет уменьшить скорость вращения, но получить момент при той же мощности. Частотный контроллер электродвигателя делает то же самое, но еще на этапе подачи энергии в обмотки.
sim31r
В коллекторном моторе обычном нет хитрого контроллера. Мотор «сам» берет нужный ток по мере возникновения препятствий вращению. Прекрасная нагрузочная характеристика, очень подходящая для транспорта. Ниже скорость, выше момент и ток потребляемый.
Да и не влияет это на Q значительно. Подразумевается крейсеркая скорость, а как она реализована уже не важно, электромотор или ДВС с коробкой передач. При разумном соотношении цена/качество приходим к Q примерно равным 1. Другие соотношения возможны, но менее практичны, есть побочные эффекты.
andersong
Спасибо, интересная тема. У меня есть подобная мысль: почему техника, созданная человеком, может нормально функционировать при температурах, комфортных самому человеку? И при отклонении температуры эксплуатации как в большую, так и меньшую сторону, уже требуются дополнительные затраты, пропорциональные отклонению температуры.
DGN
КМК потому что человек это машина созданная из элементов доступных в солнечной системе, ровно как и все прочие машины. И оптимальная температура функционирования примерно вот такая, а не как на поверхности звезды, к примеру. В общем случае, всю земную биологию ограничивает с одной стороны сворачивание белка (~60), с другой — замерзание воды.
С другой стороны, сверхпроводящий магнит требует очень сильного холода (единицы К). Автомобильный мотор желательно разогреть до 95 градусов Цельсия. Термоядерный реактор требует 150 миллионов градусов Цельсия…
Zavtramen
Потому что на данный момент почти не встречается полностью автономной техники, почти вся она управляется или обслуживается человеком, которому как раз и нужны комфортные условия.
balamutang
техника проектируется под нужный диапазон температур, тк уменьшение диапазона приведет к неработоспособности техники, а избыточное увеличение диапазона приведет к ценовой неконкурентоспособности
andersong
В том и вопрос, почему диапазоны температур, нужные человеку и технике совпадают?
balamutang
ок, упрощу ответ: примерно по той же причине по какой совпадает размер шапки с размером головы :) — ее такой специально проектируют
техника делается под температуру окружающей среды, человек эволюционировал под температуру окружающей среды, т.е. есть внешний фактор, под который мы подстроились в обоих случаях.
konst90
Потому что техника проектируется под условия эксплуатации (т.е. проживания или работы человека) же.
Если вы проектируете автомобиль — то он будет рассчитан на эксплуатацию в температуру, нормальную для региона эксплуатации. Например, в машинах для Саудовской Аравии не будет печки (но будет мощный кондиционер), а в машине для России будет и печка, и аккумулятор увеличенной емкости, и обогрев зеркал-стекол-сидений, а для некоторых регионов ещё и Вебасто опцией сделают.
Авиадвигателю «комфортнее» в -50 по Цельсию, например. Но приходится делать самолёт таким, чтобы он мог взлетать в +30.
sim31r
Полупроводникам чем холоднее, тем лучше. Есть просто особенности проектирования, параметры подстраивают под человеческие температуры (более тяжелые для электроники), и при быстром охлаждении платы могут потрескаться, нужно какие-то зазоры и компенсаторы геометрии предусматривать.
habr.com/ru/post/190180
Разгон Arduino. Под жидким азотом. 20 ? 65.3Mhz @ -196 °C
И наоборот, для скважин есть высокотемпературная электроника, работающая при температуре до +200. Всё работает, это не критический режим, просто ухудшаются параметры электроники, высокие токи утечки, заниженное быстродействие, сложности с отводом тепла.
Для механизмов другая тема. Они разрабатываются при человеческих температурах. Карбон, например. Прекрасный материал, но в космосе он становится хрупким при низких температурах и плавится при высоких. Хотя материал лучше стали во многом. Многочисленные органические материалы, пластмассы, пленки, электролиты, тоже оптимизированы для комнатных температур.
Возможно для температур -50… -80 (случайный диапазон температур) будет группа материалов лучше на порядок известных пластмасс, просто их не открыли еще. Или открыли, но не востребованы, так как при -40 они уже плавятся, а при -90 становятся хрупкими, т.е. далеко за человеческими пределами функционирования.
Интересно что обычные стали тоже становятся хрупкими при низких температурах, кроме специальных легированных. Казалось бы это металл, чем холоднее, тем должно быть лучше. А нет, большинство сталей наиболее упругие и прочные при комнатной температуре. При высоких уже окисляются и становятся ковики, при низких хрупкие.
opetrenko
может потому что техника зачастую работает рядом с человеком?
Техника для экстремальной среды тоже существует. Выбор материалов ограничивается при этом. Телегу можно и из дерева, а вот поршня в мотор уже надо из металла.
Wizard_of_light
Это потому что температура, более-менее комфортная человеку, обычно на поверхности нашей планеты поддерживается сама по себе, поэтому механизмы, рассчитанные на такие условия, будут работать без дополнительных затрат. А для отступления от температуры окружающей среды нужно усилия затрачивать, и чем дальше, тем больше.
sim31r
На часто шкафы автоматики и слаботочные подогреваются, так как электроника может начать глючить при температуре ниже 0, обычно так и пишут производители, рабочий диапазон 0… +30 например. Причем впечатление что 0 пишут наугад, не -1, не +3, а именно 0.
arheops
0 пишут не наугад
Если у вас -1 разрешенная, то у вас будет большое число переходов -1 до +1, что приводит к появлению и исчезновению льда-воды.
А лед-вода такая штука, что малейшая трещинка на плате становится дыркой(поскольку лед занимает больше обьема). Тоесть плата должна быть герметична и выпукла.
sim31r
Если на плате образовалась влага, будет окисление и часто мгновенный выход из строя. Конденсат может образоваться и при +15 градусах и высокой влажности. При влажности 100% влага будет стекать почти по всем поверхностям.
Обычно просто пишут, без образования конденсата влажность допускается. И еще одно требование, когда заносят оборудование с улицы в помещение, нужно подождать пока испарится возможный конденсат. На холодных предметах в теплом помещении может образоваться влага.
И наоборот, при типичной влажности менее 20% влаги или инея не будет ни при 0, ни при -1.
Уличные часы, телефоны, автомобили и много чего еще многократно переживает охлаждение ниже 0 градусов, естественно в сухом виде.
Скорее всего именно 0 градусов пишут просто подразумевая обычный режим температур, комнатный. Что ниже, считается чуть ли не криотемпературами, уличным/промышленным/военным/космическим исполнением и требует отдельного дорогостоящего тестирования. Смотрю по микроконтроллерам, сердце электроники
Причем в военном исполнении 2 проблемы, очень дорого и не продадут. Хотя на севере это обычные температуры уличные.
arheops
Ну защита от конденсата — это два слоя простого лака, просто опускаем пару раз в раствор.
А защита от образования льда и деструкции — сильно сложнее.
vvzvlad
О чем вы вообще? От льда и деструкции защищает корпус. А обсуждаются температурные границы для электроники. Если на плата попала вода, то вам уже никто ничего не гарантирует, ни при -1, ни при +10.
arheops
При проходе через 0 в большинстве корпусов не исключается лед внутри корпуса.
Конденсация-вода-лед
vvzvlad
Ох. Ладно, смотрите за руками. Корпус 1х1х1м, объем — соответственно, кубометр, площадь стенок — 6м2. Влажность 50%, 20 градусов при закрытии — 9 грамм воды в воздухе. Понижаем температуру до 0 градусов, в воздухе остается 5 грамм воды, остальное конденсируется на стенах(допустим что корпус пустой внутри, а электроника размазана по стенам, хотя реально она еще поднимет площадь в пару раз точно).
9-5=4г воды. 4/6=700мг на квадратный метр, или 0.7мг на квадратный сантиметр. Не думаю, что такое количество воды в виде инея может что-то повредить на плате, покрытой лаком.
Но дело даже не в этом. Следуя вашей логике, получается, что самое страшное — это переход нуля. А это не так: не зря есть разные градации нижней температуры, -10, -40, -55.
arheops
Да пожалуйста.
Только оно может осесть не в виде инея, а обычно в виде капелек, которые имеют тенденцию затекать в щели.
А -40 — это уже прочность материалов, да, другая градация. Некоторые пластмасы и смолы, да тот же лак, становятся неустойчивыми и/или хрупкими. Да и припои некоторые — тоже.
Но мы в этой ветке вроде бы обсуждаем, почему «наугад» пишут «от 0».
u010602
Потому что наукой движет рынок, а рынок продает устройства для нашей планеты. Вполне возможно есть элементная база для работы в других условиях — мы просто пока не искали достаточно активно. Откуда человеку, который ни когда не видел моря, знать из каких материалов строить корабль?
NetBUG
Тут ещё вопрос в конструкции ТС и механизма удержания груза на нём.
Для электромотороллера Q ~ 1, а вот для самоката порядка 4-5 (мой самокат весит 14 кг, я вешу 59 в голом виде, типичная масса нагрузки ближе к 70 кг).
Но человек на самокате — это очень хорошая нагрузка, сама держится и активно стремится не упасть.
sim31r
Электромотороллер поддерживает пассажиров в сидячем положении, а на электросамокате пассажир стоит, опираясь ногой в основание. Чтобы сравнивать, можно считать что ноги это часть самоката в какой-то мере, они участвуют в движении поддерживая торс. А в электромотроллер сам поддерживает торс, ноги отдыхают полностью, нагрузка на ноги 0 кг.
Iwanowsky
Очень интересное исследование на тему транспорта! В Интернет до этого встречались аналоги, но это мне понравилось больше.
Коэффициент Q, в принципе, можно привязать к КПД транспорта. Кроме того, т.к. в вес транспорта входит и масса перевозимого топлива, то для некот. видов транспорта (особенно с очень высоким Q) в принципе можно сказать, что Q (или КПД) будет увеличиваться по мере расхода топлива.
gleb_l
Введение C(Q), построение гипотезы, ее оценка снизу/сверху и пруф просто блестящие!
nonpar
Необходимое условие любой успешной транспортировки — сохранность груза. Отсюда, во-первых, прочностные требования к «таре» должны примерно соответствовать прочности груза, для которого она предназначена. Во-вторых, если речь идет о грузах, для которых не определено понятие прочности (жидкости, сыпучие вещества) — «тара» для них должна обеспечивать всего лишь изоляцию груза от окружающей среды и её факторов. Исходя из этого, для нефтеналивных танкеров, например, показатель заметно больше 1. Трубопроводы, кстати, тоже транспорт; как для них посчитать Q, большой вопрос. Если же рассматривать перевозку через открытый космос, то космический «супертанкер», функционирующий в условиях невесомости, отсутствия атмосферы и контролируемых ограниченных ускорений при его перемещении, может иметь Q ещё больше, чем судно-супертанкер. А ведь есть ещё плоты — конструкции для транспортировки «самонесущих» грузов.
eugeneb0 Автор
Где-то так. Я тоже интуитивно ощущаю, что здесь важна связь между прочностью груза и прочностью транспортного средства.
А плот — интересный вопрос. Плоты в природе ведь естественным путём иногда образуются. Это транспортное средство не совсем сделано человеком )
nonpar
Плот, самокат, лыжи/коньки — явления одного порядка. В контексте статьи их, вероятно, нельзя называть транспортными средствами.
catharsis
у самоката (или например электроскейта) есть рама, передающая вес груза на колеса,
так что самокат, чемодан на колесиках и карьерный самосвал в данном контексте похожи (и, конечно, чем размеры рамы меньше, тем удельная грузородъемность больше — из тех же соображений, как про муравья выше).
Лыжи, ледянка, плот или наливной танкер принципиально другие, потому что опираются на большую площадь и не имеют несущей конструкции, способной длительно выдерживать перевозимый вес.
vadimr
Если разместить на транспортном средстве произвольно взятый груз, значительно превышающий его вес, то оно потеряет остойчивость и другие динамические характеристики. Вот и вся причина. Меньше своего веса таскать неэффективно, а больше – опрокинется.
eugeneb0 Автор
Интересная мысль. Мне кажется, тут что-то слишком упрощено. Но я подумаю.
Jogger
Только наверное всё же зависимость от массы, а не от веса. А то вес у дирижаблей так-то отрицательный будет.
eugeneb0 Автор
Ох, вопрос «вес или масса» меня чуть не съел при написании этой статьи. Потому что, на самом деле, нужно ни то, ни другое. Мы же хотим измерить выдерживаемую конструкцией нагрузку по отношении к её массе. Но так, чтобы было безразмерно. Так что более-менее точным определением будет Q = «вес груза, делённый на сухую массу конструкции, и делённый на g». В тексте решил не усложнять, но, похоже, зря: многих эта неоднозначность сбила с толку.
Tim_23
Сравнивать ракету и «многоразовую» технику наверно некорректно еще и потому, что материалы в ракете могут работать уже в зоне предела текучести(и даже выше) и ограниченного временного отрезка, без циклических нагрузок.
Не совсем понятно также, почему для Протона Q считается как соотношение сухой массы к полной массе, а на ранее приведенных графиках, насколько я понял вы брали отношение сухой массы к массе груза(или полезной нагрузки) (или не так?)
Опять же, если сравнивать с автомобилями, массу топлива и прочих жидкостей учитываем или нет?
eugeneb0 Автор
Мы считаем Q не совсем для Протона, а только для его первой ступени. Это имеет смысл, т.к. первые ступени являются практически самостоятельными транспортными средствами (а Titan II, например, теоретически вообще мог выйти на орбиту одной первой ступенью).
При вычислении Q нас в первую очередь интересует инжереная сложность противостоящей нагрузке конструкции (топливо ей не противостоит и ничего почти не стоит). Какой нагрузке противостоит первая ступень? Свой стартовый вес, вес топлива, и вес всего, что сверху, всё это с учётом перегрузки. Делим это на сухую массу ступени (именно она всё это держит). И делим на g (исключительно чтобы оперировать безразмерным параметром).
Absent
Эта статья — то ли притягивание фактов «за уши», то ли открытая фальсификация фактов.
Первые же взятые наугад несколько ссылок в гугле опровергают основной постулат данной статьи: www.google.com/search?q=вес+и+грузоподъемность
Например, calcsoft.ru/skolko-vesit-kamaz — несколько таблиц как раз на заданную тему показывают, что отношение массы автомобилей КамАЗ к их грузоподъемности составляет величину около 2.0
konst90
2.0 — это отношение полной массы к грузоподъёмности. А полная масса — это масса с грузом.
Возьмем первую же строку. КамАЗ 4308.
В вашей табличке «масса со снаряжением» 11500 кг, грузоподъёмность — 5500 кг. Сайт КамАЗа нам говорит:
Грузоподъемность автомобиля, кг 5730
Снаряженная масса, кг 6020
Почти совпадает.
MacIn
Немного странная таблица.
К примеру, взять самосвал КамАЗ 65115 — указано «снаряженная масса» 25 тонн, грузоподъемность 15.
При этом КамАЗ-6522 (тоже самосвал) если верить википедии:
Снаряженная масса а/м, кг — 13950
Грузоподъемность а/м, кг — 13500
т.е. 1 к 1.
Да и описание в шапке странное:
Т.е. сначала «полный вес», потом «грузоподъемность» и аж 20-40 тонн, что нереально.
На деле это полная масса, как указано изначально.
В общем, пмсм, намешано в кучу.
Serhii-Che
Из Вашей статьи получается, что прогресс не приносит никакой выгоды и технический прогресс стоит на месте, меняется только форма, материалы, технологии…
Грустно как то (
eugeneb0 Автор
Не грустите. Не так всё плохо. А про прогресс мы в четвёртой части поговорим ))
KOPiten
Касательно грузовых судов (корабль может быть только военным), Q значительно больше единицы (3-10). Разного рода сухогрузные суда и, в частности контейнеровозы, перевозят груза, измеряемого в тоннах, меньше чем могли бы исключительно потому, что объем занимаемый грузом очень велик. Контейнеровозы, паромы, пассажирские суда и прочие возят в основном воздух. Если грузить их чем-нибудь более тяжёлым, тогда ваш Q может быть более 20 (балкеры или танкеры, например).
eugeneb0 Автор
Про танкеры я написал в разделе о данных, Вы, видимо, не обратили внимание. Значительная часть нагрузки танкера воспринимается окружающим морем. Сухопутным аналогом этого был бы грузовик с внешними подпорками, чтобы борта не разваливались. Но таких нет.
В целом же — было бы интересно взглянуть на данные.
Iwanowsky
А для дирижабля окружающий воздух принимает значительную часть нагрузки.
eugeneb0 Автор
У танкера нефть давит изнутри на корпус. Этому давлению противостоит давление внешней воды. Оно снимает значительную часть нагрузки, которую иначе пришлось бы выдерживать прочному корпусу и, таким образом, позволяет сделать его легче.
У дирижабля груз размещён снаружи. Покажите мне, как воздух облегчает структурную нагрузку на корпус в этом случае (и делает его легче)?
Iwanowsky
В современных дирижаблях груз может находиться внутри жесткого корпуса, как и баллоны с гелием или горячим воздухом.
eugeneb0 Автор
И как воздух облегчает структурную нагрузку на корпус?
vvzvlad
Если бы снаружи был ваккум, корпус бы разорвало :)
eugeneb0 Автор
Если бы снаружи был вакуум, дирижабль бы не полетел.
Но дирижабли летают в воздухе, а корабли плавают в воде, так что давайте попробуем получить ответ для этих условий.
vvzvlad
Ну, это была шутка, я попытался это передать с помощью смайлика.
eugeneb0 Автор
А. Извините, не понял.
eugeneb0 Автор
Подсказываю. На нижнюю часть корпуса корабля с осадкой 10 метров снаружи внутрь действует давление в 1 атмосферу. 10 тонн на квадратный метр. Это давление можно скомпенсировать изнутри, «уперев» в корпус много жидкого груза. Тем самым снизив требования на прочность корпуса и облегчив его.
Теперь дирижабль. На нижнюю часть его корпуса диаметром 10 метров действует разница давлений столба гелия и воздуха высотой 50 метров. Это 0.1% атмосферы, или 10 кг на квадратный метр. В 1000 раз меньше. Что не особо позволяет снизить требования на прочность корпуса и облегчить его.
eugeneb0 Автор
Del
KOPiten
Несколько натянутый довод. Все суда нагрузку распределяют на воду. В разные стороны. В таком случае их следует совсем убрать из ваших выкладок. Как впрочем и ж/д составы вместе с рельсами. А если подтягивать коэффициенты, тогда можно к современным грузовикам подтянуть асфальтовое покрытие. В общем, очень сомнительное утверждение :)
eugeneb0 Автор
Тут, конечно, есть некоторая натяжка. Но не беспредельная, поверьте.
Для простоты — мысленный эксперимент. Представим себе танкер, перевозящий… воду. Он сидит себе в воде. Изнутри наружу давит вода. Снаружи внутрь — вода. Они компенсируются. Прочность корпуса (и массу) за счёт этого можно радикально уменьшить. В разы.
А вот с сухопутным грузовиком такой номер не пройдёт. Кузову приходится полностью держать груз. Срезать разы по массе за счёт асфальта не получается.
VolCh
А если кузов положить на асфальт? Типа волокуш.
KOPiten
Вы не поверите! Танкера перевозят жидкости, удельный вес которых очень близок к… воде. Так что можете сразу считать, что что он перевозит воду. Однако, танкера уже давно двухкорпусные. Перевозимый груз отделяется от воды как минимум двумя стенками. Между грузовыми танками и водой расположены балластные танки или просто пустые помещения. Это необходимо для экологической безопасности. Конструкция танкера — это как бы термос — колба в колбе. Это так, вам для информации.
juray
Впрочем, всё равно не грузовым — если говорить о современности. Вот только — а почему нужно придерживаться такого ограничения? Так-то, например, клиперы были вполне грузовиками.
Dolby
Интересное исследование, но ИМХО не совсем корректно проведено. Я считаю что неправильно сравнивать наземные/водные виды транспорта с авиацией и ракетной техникой.
Напомню:
есть огромная разница в перемещении грузов по горизонтали, где мы сопротивляемся трению и лобовому сопротивлению воздуха, пропорционального квадрату скорости, и по «вертикали» где нам необходимо побороть тоже самое трение воздуха (переменное по высоте), лобовое сопротивление (переменное по высоте) + гравитацию. Авто конечно тоже может двигаться с уклоном, но вот водные виды транспорта движутся строго горизонтально без преодоления уклонов
Полагаю правильно было бы выполнить расчеты для каждой категории транспорта по отдельности, а перемещаемую расчетную грузоединицу представить как совершаемую работу. Согласитесь, тащить груз в гору с уклоном 30 град. совсем не то же самое что тащить под уклон, и уж тем более это никак не сравнить с ракетой выводящей груз на орбиту высотой 400 км. Для морского и речного транспорта необходимо еще учитывать течение и вообще кучу всего, например учесть массу топлива, для ракет это суперкритично
eugeneb0 Автор
Вот мне тоже на первый взгляд кажется, что не должно быть корректно. А Q всё равно у всех более-менее одинаковый. Что и удивительно. Видимо, есть какие-то общие причины, несмотря на настолько разную природу транспорта. (Кстати, тут вот подумалось: какая-нибудь канатная дорога, что тащит груз в гору, тоже вряд ли же имеет Q = 0.03 или 30. Надо бы поискать цифры).
Germanjon
В случае канатной дороги ещё возникает избыточный балластный вес — противовесы, опоры. Нужно ли их учитывать?
OriSvet
Грузовой самолёт с «сухим» весом почти в 300 тонн лично мне неизвестен.
Самый крупный из летающих, Ан-225 — Q=250\250=1, с оговорками
A380F, существует в линейке, но ни одного не заказано — Q=150\274=0,54
В районе 180 тонн точечка почему-то одна.
Ан-124 — Q=120\178,4=0,67
С-5 Galaxy — Q=130\172,3=0,75
747 Dreamlifter — Q=113,4\180,53=0,63
747-8F — Q=134,2\191,1=0,70
В районе 120 тонн:
Ан-22 — Q=60\118,72=0,51
C-17 Globemaster III — Q=77,5\122,01=0,64
Более лёгкие проверять не стал, поскольку их реально дофига.
В остальном не разбираюсь.
eugeneb0 Автор
Там в данных все источники указаны. За что купил, за то и продаю. В частности, Википедия для Ан-225 даёт пустой вес как 285 тонн.
OriSvet
Я все данные брал из Википедии. Вес в 285 тонн для пустого борта есть только в англоязычной статье.
opetrenko
Роликовые ботинки считаются?
или тележки, для передвижения мебели?
Или надо сначала моторчик приделать?
Думаю даже с моторчиком Q будет довольно большое.
xenon
а что такое ролик — это и есть тележка. Можно стакан возить или книжку. Но для нормального груза — надо тележку увеличить примерно до размеров кузова грузовичка. да, добавить мотор. бензобак или аккумулятор. Ну и место для водителя, кто-то же решает, вправо или влево ехать. Руль. Ну вот мы автомобиль и изобрели.
homocomputeris
Смотрю на таблицу и пытаюсь понять: как именно 2.5 и 3.5 тяготеют к единице?
arheops
Логарифмически, конечно.
Имеется в виду, что крайне близко к 1 по отношению к возможным значениям(+бесконечности).
eugeneb0 Автор
Хороший вопрос!
Вот у нас есть транспортные средства с массами от 100 до 107 килограмм. И есть грузоподъёмности примерно в том же диапазоне. Предположим, что эти величины полностью друг от друга независимы. Тогда, если мы начнём вычислять величину Q, то где-то 300 кг поделятся на 900 тонн, а где-то 2000 тонн на 5 тонн (поскольку связи нет, пары значений для каждого средства случайны). В итоге значения Q будут разбросаны от 10-5 до 105. Это и есть ожидаемый диапазон разброса для «нулевой гипотезы» об отсутствии связи между массой и грузоподъёмностью. С ним надо сравнивать, когда мы выясняем, тяготеет ли Q к чему-то.
Реальный разброс — от 0.3 до 3.5. То есть, в 100 тысяч раз меньше теоретически возможного. На этом фоне отклонение от единицы в 2-3 раза, очевидно, настолько ничтожно, что «нулевую гипотезу» приходится с треском отбросить.
homocomputeris
Это никак не объясняет, почему 0,6 и 3,6 — почти единица и почему разницей в два-три раза можно просто пренебречь.
Можно сделать транспортные средства для перевозки одного атома, там «теоретический» разброс ещё больше будет. После этого и порядок 5 будет «почти единицей» по сравнению с -25.
eugeneb0 Автор
Эх… «привези мне, батюшка, чудо-юдище для утех сексуальных» (анекдот про аленький цветочек). Пойдём сложным путём.


Вот распределение F = dN/dLog10(m) логарифмов масс ТС в данной работе:
(Логарифм десятичный, масса в килограммах)
Вот, аналогично, распределение G = dN/dLog10(Load) логарифмов нагрузок:
Их характерная полуширина — 3-4 порядка. Характерная, т.е. не зависящая от наличия единичных машин для перевозки атомов, и даже от включения/исключения класса электрокаров, на котором часть народа выше так сфокусировалась ))
Логарифм Q есть логарифм отношения L/m, то есть разница логарифмов масс и грузоподъёмностей. Характерная полуширина этой разницы — вообще порядков 10.
Вопрос. Дано два независимых распределения F(x) и G(y). Какова будет функция распределения величины x — y? Ответ: это свёртка функций F(x) и G(-y).
Т.е., распределение логарифма Q — это свёртка распределений логарифма масс F и
минус-логарифма грузоподъёмности G. Если, конечно, между первым и вторым нет связи.
Какова характерная полуширина этой свёртки? Можно, конечно, посчитать точно, но для не слишком экзотических распределений она — примерно половина ширины распределения F(m) — G(m). Т.е., примерно 5 порядков. Опять же, характерная, т.е. не зависящая от единичных примеров/выпадов. Важно также помнить, что операция свёртки вообще имеет тенденцию «замыливать и обезличивать» входные функции, устраняя особенности вроде сильных пиков или далёких выбросов.
Итак, если m и L(oad) никак не связаны, следует ожидать, что распределение величины Log(Q) будет чем-то колоколоподобным с полушириной около 5 порядков.
Мы наблюдаем нечто колоколоподобное, но с полушириной в 0.5 порядка.
Какова вероятность, что подобная «узкая» выборка образовалась случайно в то время как мы ожидаем «широкую»? Считаем хи-статистику, смотрим по таблицам вероятность, что результат — случайность. Я этого не делал, но поверьте, в данном случае она астрономически мала.
И будет мала, пока наблюдаемая характерная полуширина логарифма Q не достигнет хотя бы половины полуширины каждого из распределений, т.е. эдак 1.5-2 порядков. Можно посчитать точно, при необходимости. Но при такой колоссальной разнице ожидаемого «независимого» и реально наблюдаемого распределения в этом нет нужды, статистика заменяется здравым смыслом.
eugeneb0 Автор
Впрочем… я тут подумал. Вот более простой способ проиллюстрировать идею.



15 точек (столько же, сколько у нас классов). У точек логарифм грузоподъёмности линейно зависит от логарифма массы. Но — добавлен разный уровень шума s. От s = ±0.5 порядка и выше. Это в точности эквивалентно разбросу Q в 10s раз.
Проведём через каждую группу линию и посчитаем, какова же вероятность того, что данные точки сложились в эту линию (или, возможно, лучшую) при разных уровнях разброса Q.
±0.5 порядка (т.е. полуширина отклонения от единицы до 3-х раз::
Вероятность, что это случайность — 1.9*10-11
±2 порядка (т.е. полуширина отклонения от единицы до 100 раз):
Вероятность, что это случайность — 1.3*10-5. Уже можно задуматься.
±7 порядков:
Полный шум (p = 0.47)
Т.е. видно, что отклонения Q от единицы раз эдак до тридцати даже выводов не ломают.
Germanjon
Пример — контейнер для хранения и переноски радиоактивных веществ. Много килограмм свинца для переноски одной небольшой пробирки
santa324
Хорошая статья, интересная тема затронута.
Почему все транспортные средства тяготеют к грузоподьемности равной своему весу легко прийти из простых рассуждений: Если есть ТС способное везти в 10 раз больше собственного веса — тогда чтобы увеличить грузоподьемность на 5% надо уменьшить сухую массу в 2 раза. А если ТС можетвезет 1/10 собственного веса — тогда уменьшив сухую массу всего на 10% получаем прирост грузоподьемности в 2 раза.
При таком раскладе делать ТС с массовым совершенством сильно больше единицы выгодно только если это очень дешево получается.
Аналогично для первой ступени ракеты делать ее массовое совершенство выше примерно 15 (как у современных ракет) не целесообразно так как экономия массы на фоне массы полезной нагрузки (в виде заправленной второй ступени) незначительна. Если только вы не собираетесь уменьшать количество ступеней или сажать ступень на своих движках.
И в статье совсем не ракрыта тема стоимости топлива. Для самолетов, слышал мнение, что стоимость топлива дает основной вклад в стоимость перевозки грузов а не стоимость самолета.
eugeneb0 Автор
Интересное рассуждение. Думал о чём-то похожем в качестве возможного объяснения, но не сформулировал так чётко, как у Вас. Похоже на правду.
Googlist
Статя очень интересная, очень напомнила такую штуку.
И вот еще. Какое тут Q будет?
Тягач примерно 7 тонн и полуприцеп 8. Автор их сознательно исключил ибо они не попадают в теорию однако ирл перевозят грузов почти как железная дорога с рельсами. Ограничение на перевозку в ~24 тонн только в законе — зависит от прочности дорожного полотна.
eugeneb0 Автор
Трудности с делением 24 на 15? Q = 1.6 получится. Где непопадание?
Сравните это с диапазоном 10-5....105, который бы наблюдался, если бы массы и грузоподъёмности действительно абсолютно не зависели друг от друга (диапазон и тех, и других — от 102 до 107 килограмм).
numitus2
del
numitus2
А еще есть всякие тележки на которых перемещают дома. Для них не считали?
eugeneb0 Автор
Не-а. Мне и в голову не пришло. Любопытно было бы прикинуть.
vvzvlad
Вес дома, судя по паре статей — 3000-7000т. Вряд ли колеса и домкраты будут весить больше 1000т, что дает нам как минимум Q в 3-7
u010602
Вы упускаете тягач.
vvzvlad
Он с большим запасом влезает в 1000т, при весе в 6т :)
Там, в общем-то, можно обойтись без тягача, просто лебедка, которая тянет сантиметры в минуту, но с большим усилием. Пары тонн хватит.
u010602
Лебедке нужен источник питания, и его нужно внести в уравнение. Так-же как и массу стоячего груза. Относительно массы дома — ее можно прикинуть по количеству колес у платформы что его везет. Т.к. давление колеса на дорожное полотно строго регламентировано в США и ЕС. Насколько я вижу, там вполне обычные прицепы, а значит и масса дома не сильно больше массы зерновозов, просто дома объемные.
Пожалуй дом в неск тысяч тонн двигать будут по рельсам при помощи гидравлических домкратов.
worldmind
Наблюдение прикольное, но не стоит сильно нагнетать пессимизм — в космос дорого летать всё-таки из-за того, что надо всё брать с собой и преодолевать с этим грузом гравитацию, если добывать например большую часть на условной Луне, то должно быть полегче.
iozjik
С интересом жду продолжения статьи. Любопытно, когда же будет объяснено название — пока в тексте не упоминаются пружины, но подозреваю, что это ключевая аллегория для понимания следующих частей.
didkovskyi
Не совсем понял, почему массу топлива в ракете отнесли к полезной нагрузке.
eugeneb0 Автор
Знаете, Вы очень хорошо задали вопрос. Настолько, что я сам осознал некоторую неточность в статье. И вынес ответ в отдельный комментарий: habr.com/ru/post/437910/#comment_19684854
Спасибо!
eugeneb0 Автор
Про ракеты и топливо.
В статью действительно закралась одна серьёзная неточность. Неочевидная. Её заметили несколько человек. Но благодарен я больше всего пользователю didkovskyi.
Он не стал размахивать совой на глобусе, обвинять меня в намеренной подгонке данных, и пытаться перечислить все шершавости текста (а куда же без них?). Он сфокусировался на главном, задав один-единственный простой вопрос:
И вот тут я, попытавшись сформулировать ответ, разглядел, наконец, эту неоднозначность в незамутнённом виде.
Есть два разных Q. И они очень похожи.
Первое, Q1, характеризует экономическую эффективность системы. Оно равно массе груза к сухой массе ТС. Без топлива. Почему без? Потому что именно в таком рассмотрении вырисовывается сильная закономерность Q = 1. Со страшной силой. Вероятность случайного совпадения — на уровне 10-300. Можно выкинуть конвейерную ленту, подозрительные электрокары, ракеты и ещё половину точек — всё равно p-value остаётся астрономически ничтожным. Спрашивать, почему мы смотрим именно без топлива — это все равно что требовать у Ома, чтобы он не ток от напряжения мерял, а что-то другое. Именно там возникает закономерность. Видимо, «так устроена природа». Впрочем, очень хорошее, на мой взгляд, объяснение феномену предложил santa324.
И есть другое Q, назовем его Q2. Оно характеризует способность системы выдерживать механическую нагрузку. Равно весу груза плюс топлива, деленным на mg, где m — маса сухой конструкции.
Для подавляющего большинства транспортных средств Q1 ? Q2 ? 1. Именно это сходство не позволило ни мне, ни десятку человек, которых я просил вычитать и «разбомбить» статью перед публикацией, заметить неоднозначность. И потребовались тысячи читателей Хабра, чтобы обратить на неё внимание.
Существенная разница возникает именно у ракет. Из-за массы топлива. Так, у первой ступени Протона Q1 — это масса всех заправленных вышестоящих ступеней плюс ПН, к сухой массе ступени. Где-то 7.7. А вот Q2 действительно зашкаливает за 34.
И здесь встаёт вопрос: так к какому же Q применимы полученные формулы стоимости?
Я утверждаю, что к Q2. Именно им определяется способность системы держать нагрузки, а значит, и инженерная сложность.
Простой мысленный эксперимент. Вот Вы — конструктор первой ступени Протона. Есть два варианта нагрузки, на которую её нужно рассчитывать:
а) Q1, нагрузка 240 тонн (только верхние ступени).
б) Q2, нагрузка 1068 тонн (вес верхних ступеней и топлива, да с учётом перегрузки)
Очевидно, что если выбрать Q1, то ракета не то что никуда не улетит, а просто порвётся на этапе заправки топливом. Значит, конструировать её надо под значительно большую нагрузку Q2. С соответствующими инженерными трудностями и более высокой стоимостью.
Сумируем:
1. Q1 характеризует экономическую эффективность транспортного средства, Q2 — инженерную стоимость.
2. Для большинства человеческих ТС Q1 ? Q2 ? 1.
3. Однако у ракет Q1 ? 1, Q2 — несколько десятков.
3. У первых ступеней ракет Q1 ? 3-10, Q2 — несколько десятков. Последним и определяется (в значительной степени) их высокая стоимость.
Это, надеюсь, разрешает противоречие по ракетам, на которое с разной степенью отчётливости пытались указать умные люди.
u010602
Подгонка результата под ожидание, разве нет?
eugeneb0 Автор
Это Вы меня красиво вычислили. Я тут два года подгонял-подгонял, всё думал, как бы ещё фазы Луны использовать, а тут Вы раз — и поймали меня на горячем. Круто )
Ладно, давайте серьёзно. Вы путаете подгонку описания под данные и подгонку данных под описание. Первое, в общем — наука. Второе… не будем о грустном.
Опасная это путаница, будьте осторожнее. Я без иронии.
justserega
Это нормальная практика в научном мире, когда работу исследователя проверяют другие и находят методологические ошибки. Никто же не говорит, что это умышленная подгонка — довольно часто человек вовлеченный в расчеты или эксперимент не видит эти ошибки (по многим причинам).
Как известно экстраординарные утверждения требуют экстраординарных доказательств. Мне кажется как простое эмпирическое правило для быстрой оценки вполне имеет право на существование, а вот на закон не тянет.
Например, я взял самые большие самосвалы (получилось далеко от единицы):
ru.wikipedia.org/wiki/Liebherr_T282B (Q = 1.4)
ru.wikipedia.org/wiki/БелАЗ-75710 (Q = 1.25)
А в случае разных видов техники начинает топливо и среда оказывать влияние. Как идея для повышения предсказательной силы можно попробовать усовершенствовать формулу как-то так:
(полезная нагрузка) / (сухая масса + масса топлива) ? 1 ± 0.3
u010602
Я просто считаю, что у ракеты на самом деле Q мизерное, и ракету нужно рассматривать как конец линейной части закона, где возможности уже исчерпаны и нет возможности Q сделать даже 1. А вы просто вытягиваете эти точки, чтобы продолжить линейный сегмент. Было-бы что-то за ракетами — вам скорее всего пришлось выкинуть еще что-то, потом еще что-то из расчетов, что-бы сохранять положение около 1.
С другой стороны если вы хотите брать только двигатель и шасси без топлива — то нужно и везде так делать. И везде топливо записывать в полезную нагрузку. Заодно уйдем от запаса хода, который у всех разный.
chersanya
Из этого вашего сообщения следует, что для описанной в посте закономерности нет заметной разницы, брать Q1 или Q2. Верно?
Тогда ещё более непонятно это обоснование выбора Q1 вместо Q2, т.к. из цитаты выше следует, что ровно такая же закономерность наблюдается и для Q2.
eugeneb0 Автор
Для транспортных средств, у которых масса топлива, грубо говоря, составляет не более половины массы ТС, разницы действительно нет. Хоть Q1 берите, хоть Q2. Они примерно одинаковы и оценка стоимости тоже будет примерно одинаковой.
Но если масса топлива существенна (как у ракет), то эти параметры расходятся. И инженерную сложность (равно как и стоимость) тогда оценивает Q2.
chersanya
Это всё понятно, но неясно как согласуются утверждения
и
В первом вы говорите, что выбрали Q1 потому, что в таком случае получается закономерность Q = 1. Во втором — что для большинства Q1 почти равно Q2, т.е. получается что для демонстрации закономерности не важно, какое из них брать.
Wizard_of_light
Я бы ещё разделил транспортные средства (агрегаты, самостоятельно несущие груз) и транспортирующую инфраструктуру типа тех же канатных дорог, эскалаторов, транспортёров, трубопроводов и т. п. Заодно исчезнут неопределенности типа учитывать ли рельсы с поездом, асфальт с автомобилем, воду с судном и воздух с самолётом — это будет зависеть от того, оцениваем ли мы транспортную систему в целом, либо только элемент этой системы — транспортное средство.
YMA
Ещё что не было сильно затронуто в обсуждении совы и глобуса — прочность структуры при ее увеличении растет квадратично, а вес — кубически. Поэтому, например — шины игрушечной машинки можно сделать из пенопласта, и она будет вполне пригодна для перемещения. Если сделать из пенопласта колесо карьерного самосвала — сомнётся, не тронувшись с места. Отсюда, на мой взгляд, и выходит некий типичный Q для структур сопоставимых размеров — он снижается от достаточно большой величины для муравья до минимума для гигантских динозавров.
PS: выходит, Гигантские Боевые Человекоподобные Роботы нереальны при имеющихся материалах?
oracle_and_delphi
Смотря насколько гигантские.
Типичный ОБЧР — вполне укладывается в прочность стали (он ростом — ниже стальной Эйфелевой башни), просто его грунт не удержит, и он в него будет проваливаться в него «по колено», как человек в рыхлый снег, при каждом шаге.
Wizard_of_light
Ну, если посмотреть на Big Muskie, то кажется, что реальны :)