10.04.2019 23:39
xcont 17 8000 Источник
Часть 0: Фракталы в простых числах.
Часть 1: Фракталы в иррациональных числах.



В статье присутствуют Gif и контрастные картинки. У эпилептиков может случиться эпилептический припадок.

В предыдущей статье мы рассмотрели алгоритм визуализации двоичных последовательностей. Давайте вспомним.

Берем двоичную последовательность. В качестве примера несколько первых бит фрактальной последовательности, рассмотренной в предыдущей статье:

$Q_n=\lfloor n\sqrt{2} \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



0100110110010011001001101100

Рисуем квадратное клеточное поле. Расставляем биты у верхней границы. Расстояние между битами — две клетки:



Для каждого бита рисуем по диагонали пунктирную траекторию (через клетку). Для нулей первый штрих рисуем вправо:



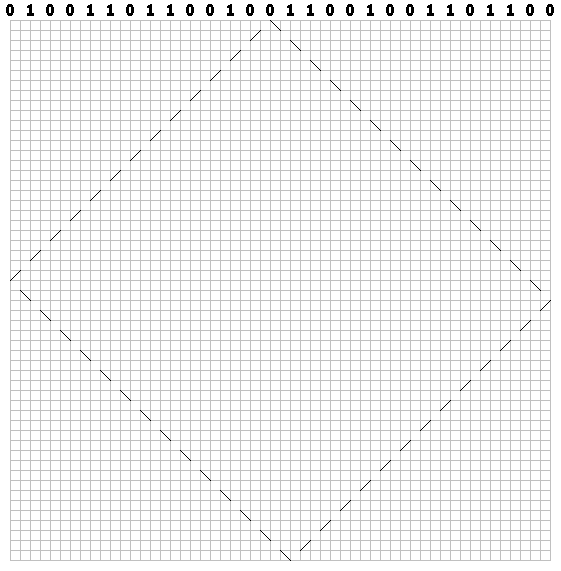
Для единиц — влево:



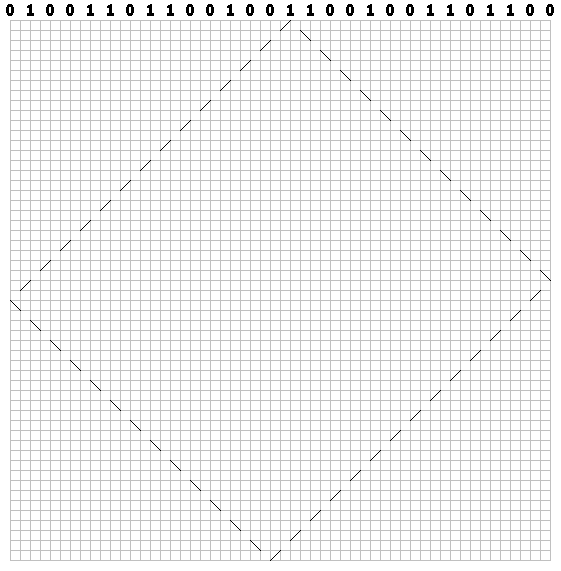
Нарисовали траекторию для каждого бита. Получили «бильярдный» паттерн:



Идентичный паттерн (без дефекта по диагонали — последовательность бесконечная, мы же ее визуализировали как конечную последовательность) можно получить другим способом. Инвертируем каждый четный бит в последовательности:

0001100011000110011100111001

Далее для каждого бита рисуем вертикальные пунктирные линии:



Расставляем биты слева, рисуем горизонтальные линии:



Совмещаем:



После написания первой статьи, оставались нерешенными два вопроса:

1. Можно ли нарисовать фрактальный паттерн для иррациональных чисел. Можно. Вопрос решили в предыдущей статье. На картинке выше — часть фрактального паттерна для $\sqrt{2}$. Если выделить одну из кривых на этом паттерне:



Получим известную фрактальную кривую — «Fibonacci word fractal».

2. Второй вопрос — можно ли написать алгоритм, закрашивающий паттерн:



Решением второго вопроса займемся в этой статье. Раскрашивать паттерны будем с помощью ткацкого станка, работу которого сымитируем с помощью JavaScript.



На схеме выше — самый простой станок. Он состоит из двух рамок, через которые протянуты нити. Рамки соединены с педалями. При нажатии на одну из педалей, одна из рамок поднимается. Нити, протянутые через эту рамку поднимаются и в получившийся зазор между нитями протягивается поперечная нить. Если четные и нечетные нити протянуть через разные рамки — получается переплетение в шахматном порядке:



В более сложных станках используется от четырех и больше рамок:


Ashford 4 Shaft Table Loom

Для того, чтобы не запутаться, какую педаль нажимать — составляют схему.



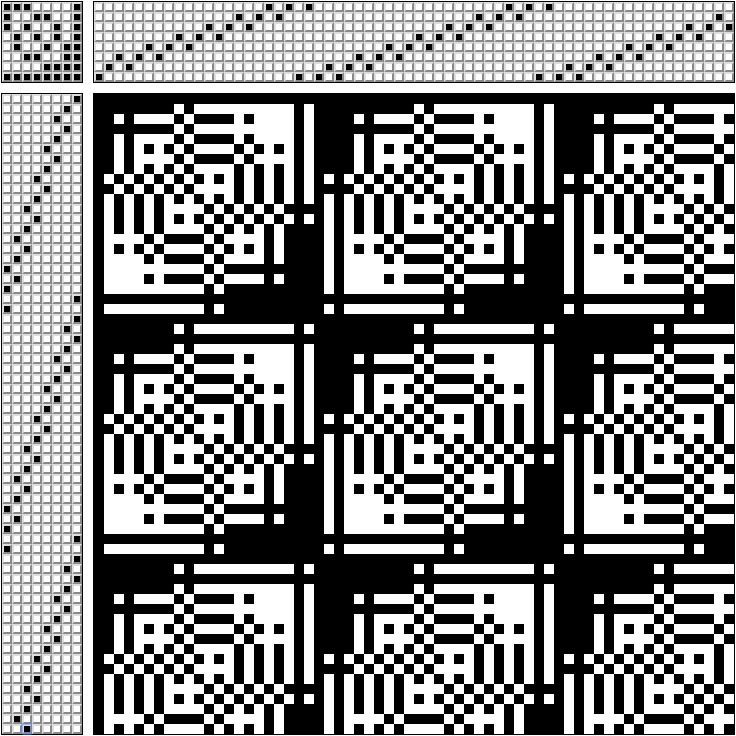
В верхней правой части схемы отмечено, через какие рамки проходят нити (схема для ткацкого станка на 8 рамок).

В левом верхнем углу — какие педали зажимать одновременно (каждая педаль связана только со своей рамкой).

В левой нижней части — в каком порядке зажимать педали.

В правой нижней части — какое переплетение мы получим. Если протягивать белую нить через черные — получим монохромный узор.

Сходу «въехать» в принцип может показаться немного затруднительным. На картинке ниже показано, как формируется ткацкий узор:



Напишем скрипт. Протягивать нити через рамки будем с помощью одномерного массива array2. В одномерный массив array1 запишем очередность зажатия педалей. В array3 (бинарный массив 8х8) запишем, какие педали зажимать одновременно.



	for(var i=0;i<length;i++){
		for(var j=0;j<length;j++){
			if(array3[array1[i]][array2[j]]){
				context.fillRect(i, j, 1, 1);
			}
		}
	}

Скрипт (работает в Google Chrome).

С помощью нашего импровизированного ткацкого станка мы можем нарисовать самые разнообразные узоры:



Но так исторически сложилось, что у среднестатистического человека не больше двух ног. Поэтому удобно одновременно зажимать не больше двух педалей. Один из самых популярных шаблонов для ткацкого станка выглядит следующим образом:



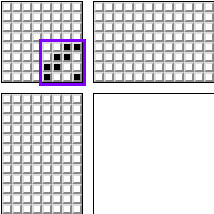
Для 4-х рамок. И его модификация для 8-ми рамок:



Неожиданно, узоры (или фрагмент узоров) сделанные с помощью этого шаблона, похожи на наши «бильярдные» паттерны. Кроме того, эти узоры получаются закрашенными:



Можно научиться подбирать «бильярдные» паттерны для ткацкого станка. Пример:



В начале статьи мы уже видели фрагмент этого паттерна.

Закончим с ткацкими станками и напишем скрипт для визуализации двоичных последовательностей. От одного из массивов можем избавиться — паттерн симметричен по диагонали. Как заполнить оставшийся массив? Элементарно:



Берем последовательность для $\sqrt{2}$. Создаем массив. В нулевой элемент массива записываем нулевой бит последовательности. Поочередно берем каждый бит последовательности. Если n-й бит = 1 — записываем в массив a[n]=a[n-1]+1. Если бит = 0 — записываем a[n]=a[n-1]-1

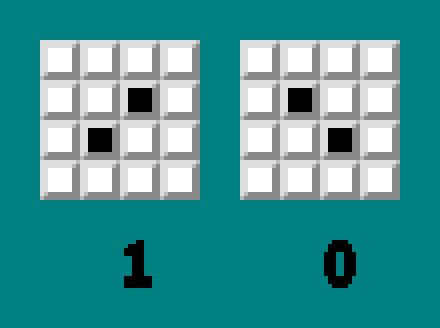
$Q_n=\lfloor n\sqrt{x} \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…\\ a_n=\begin{cases}a_{n-1}+1, Q_n=1;\\a_{n-1}-1, Q_n=0\end{cases}$





	var a=[0];
	for(var i=1;i<size;i++){
		if(Math.floor(i*Math.sqrt(2))%2==1)
			a[i]=a[i-1]+1;
		else
			a[i]=a[i-1]-1;
	}

Проверяем:

	for(var i=0;i<size;i++){
		context.fillRect(i, a[i]+50, 1, 1);
	}



Фактически мы уже получили элементарный фрактал, но продолжим.

Далее разберемся с матрицей:



Суммируем $x$ и $y$. Делим по модулю на 4. Если получившийся результат = 0 или 1 — записываем в матрицу true. Для 2 и 3 записываем false. Можем обойтись без матрицы (заранее неизвестно, какие максимальные и минимальные значения принимает a[n]). Суммируем a[x] и a[y]. К получившейся сумме добавляем некоторое число $C$ (чтобы избавиться от тех случаев, когда сумма — отрицательное число). Делим по модулю на 4. Для значений 0 и 1 закрашиваем пиксель с координатами $x$ и $y$.

Окончательный алгоритм занимает всего несколько строк:

	var a=[0];
	for(var i=1;i<size;i++){
		if(Math.floor(i*Math.sqrt(2))%2==1)
			a[i]=a[i-1]+1;
		else
			a[i]=a[i-1]-1;
	}
	for(var x=0;x<size;x++){
		for(var y=0;y<size;y++){
			q=(a[x]+a[y]+512)%4;
			if(q==0 || q==1) context.fillRect(x, y, 1, 1);
		}
	}

Визуализируем наши фрактальные последовательности.

$Q_n=\lfloor n\sqrt{2} \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$





Можно легко модифицировать скрипт для того, чтобы получить RGB-изображение:

			q=(a[x]+a[y]+512)%4;
			/*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/
			if(q==0) context.fillStyle = 'rgb(255,0,0)';
			if(q==1) context.fillStyle = 'rgb(0,255,0)';
			if(q==2) context.fillStyle = 'rgb(0,0,255)';
			if(q==3) context.fillStyle = 'rgb(0,0,0)';
			context.fillRect(x, y, 1, 1);



Выше мы к сумме a[x]+a[y] прибавляли некоторое число $C$. Если не прибавлять это число — минимальное значение суммы = -8, максимальное = 8 (для $x$ и $y$ от 0 до 750). Если убрать $C$ — в некоторых случаях сумма получается отрицательной и не кратной 4-м и для этих случаев пиксель не закрашивается (остается черным):

			q=(a[x]+a[y])%4;
			if(q==0 || q==1) context.fillRect(x, y, 1, 1);



Можно представить это так, будто часть фрактала находится ниже некоторой мнимой границы (ниже этой границы закрашиваются только отрицательные значения кратные 4-м: -4, -8, -12, ...).

Можем посмотреть, где находится эта граница:

			if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1);



Вместо деления по модулю, можем сравнить сумму с некоторым определенным значением и тем самым закрасить только один «слой» фрактала. В качестве примера возьмем среднее между минимальным и максимальным значением:

			q=(a[x]+a[y]);
			if(q==0) context.fillRect(x, y, 1, 1);



Если не понятно


Изменяя значения от минимального до максимального, можем посмотреть как меняются «слои» в динамике:



Если не понятно
Настоятельно не рекомендую открывать спойлер, если у вас эпилепсия



Кроме того, мы можем «в лоб» сравнить a[x] с a[y] и тоже получить фрактальный паттерн:

if(a[x]==a[y]) context.fillRect(x, y, 1, 1);



Следующая последовательность:

$Q_n=\lfloor n(\sqrt{2}+1) \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



Фрактал:



RGB:



Средний слой:



В динамике:



$Q_n=\lfloor n\sqrt{3} \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



Фрактал:



RGB:



Средний слой:



В динамике:



$Q_n=\lfloor n(\sqrt{3}+1) \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



Фрактал:



RGB:



Средний слой:



В динамике:



$Q_n=\lfloor n\sqrt{5} \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



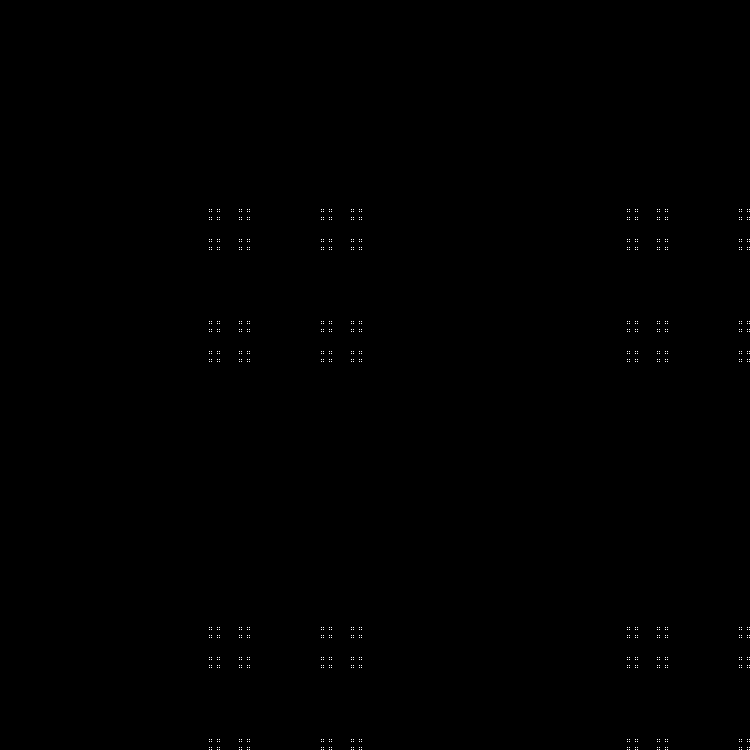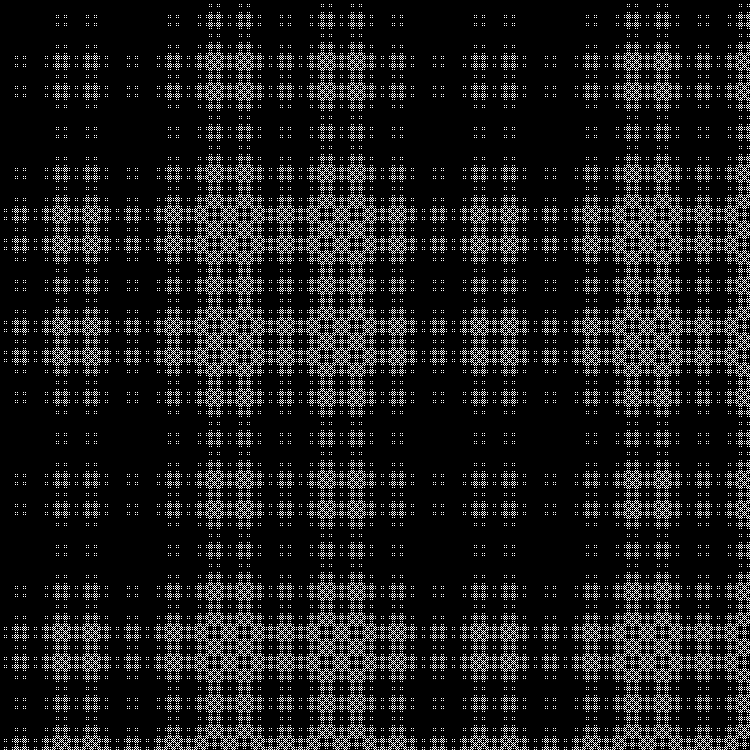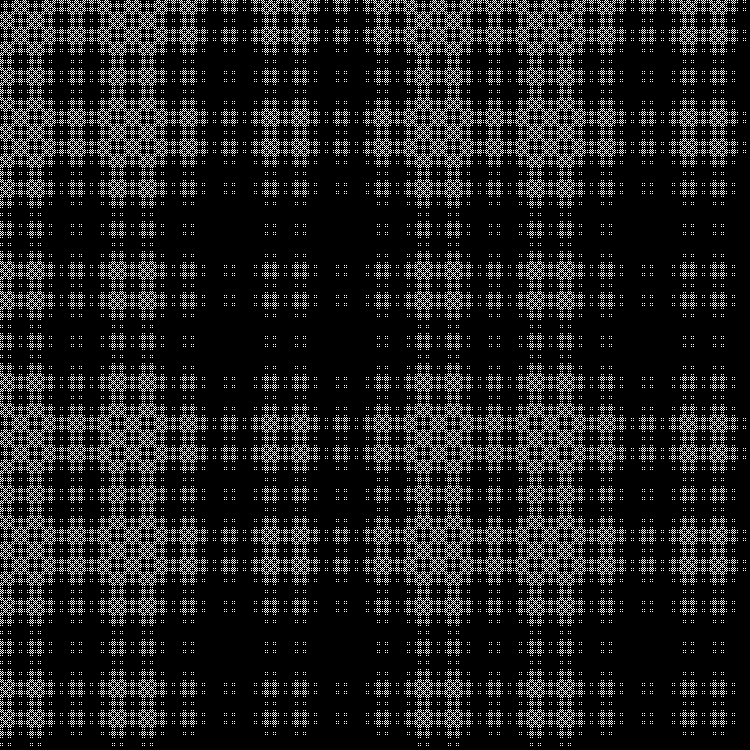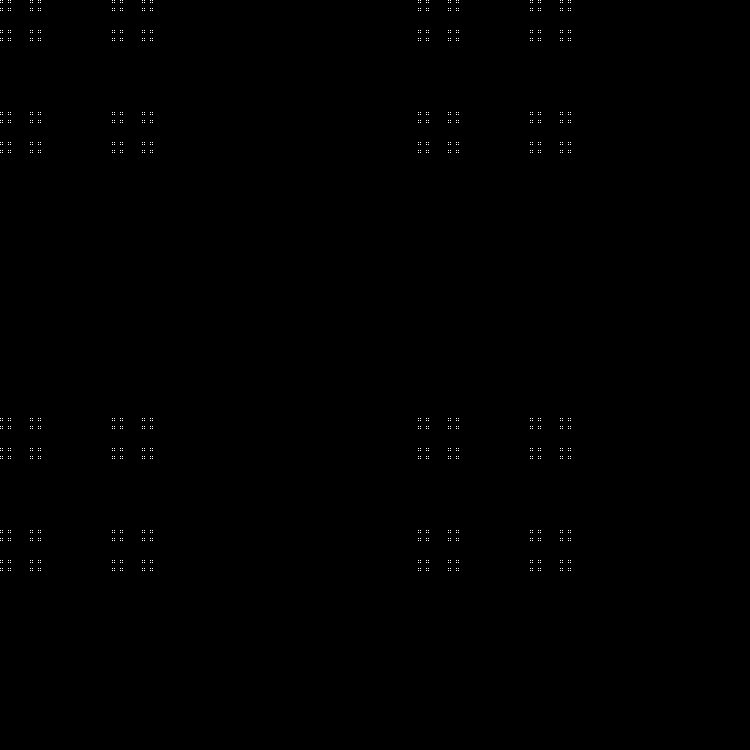
Фрактал:



RGB:



Средний слой:



В динамике:



Ну и наш любимый фрактал (часть этого паттерна можно нарисовать с помощью бильярда, с размерами сторон равными числам Фибоначчи):

$Q_n=\lfloor n(\sqrt{5}+1) \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



Фрактал:



RGB:



Средний слой:



В динамике:



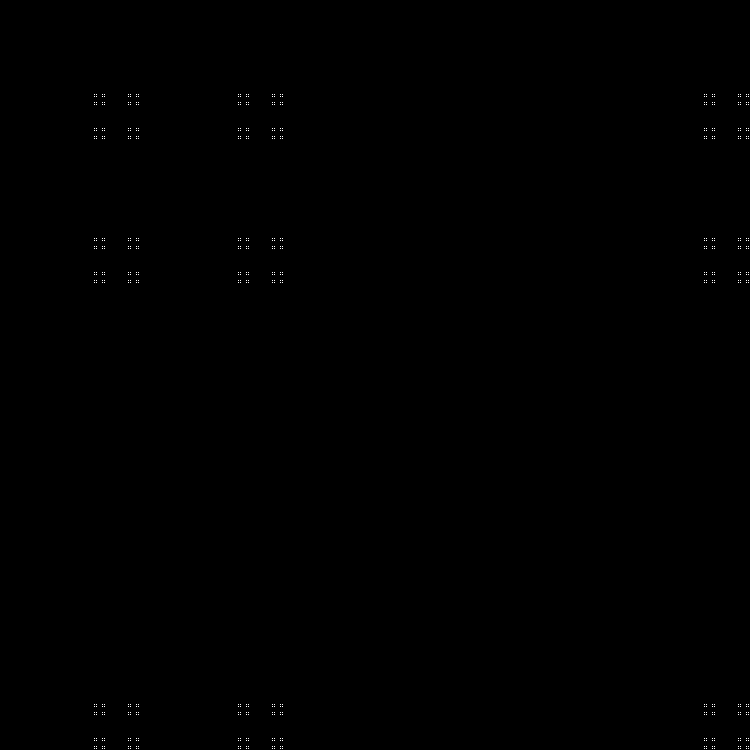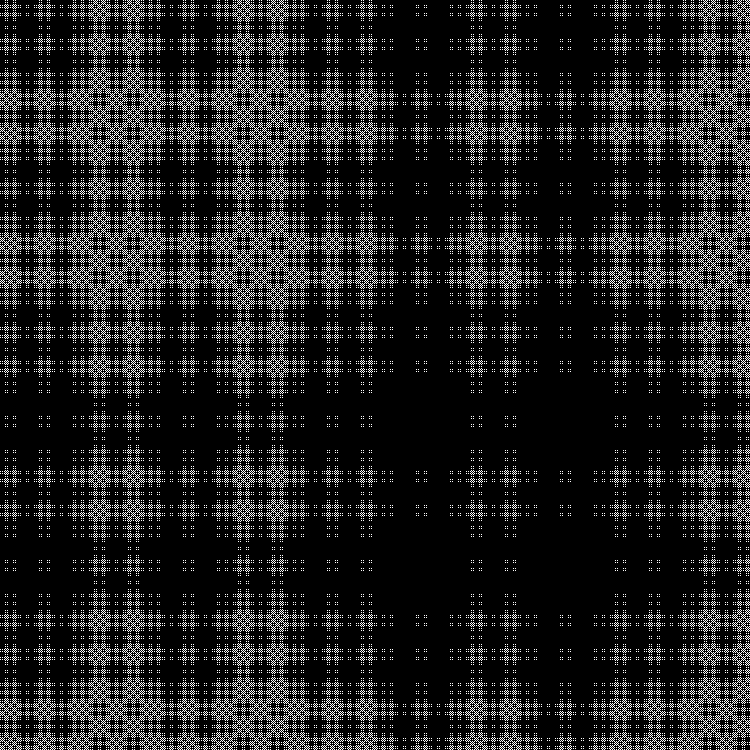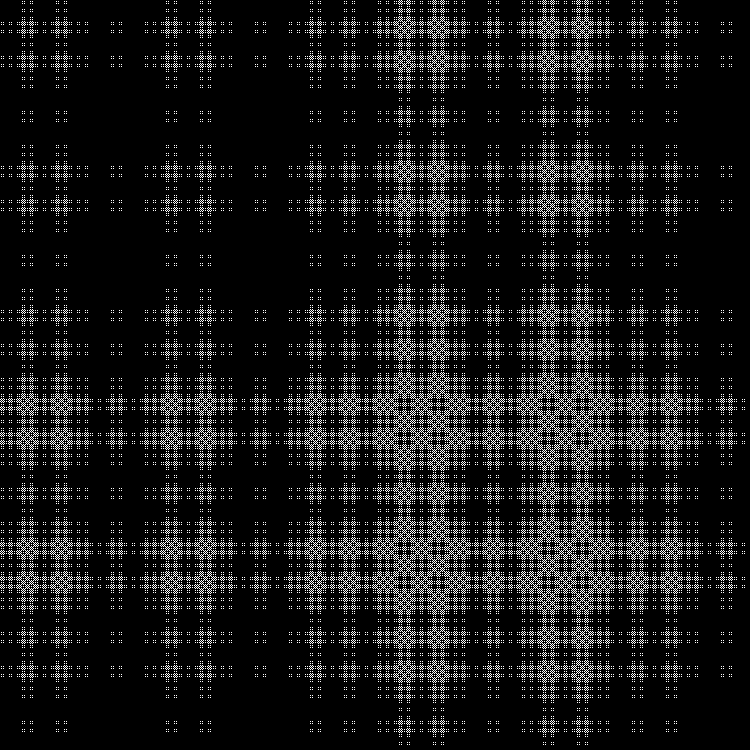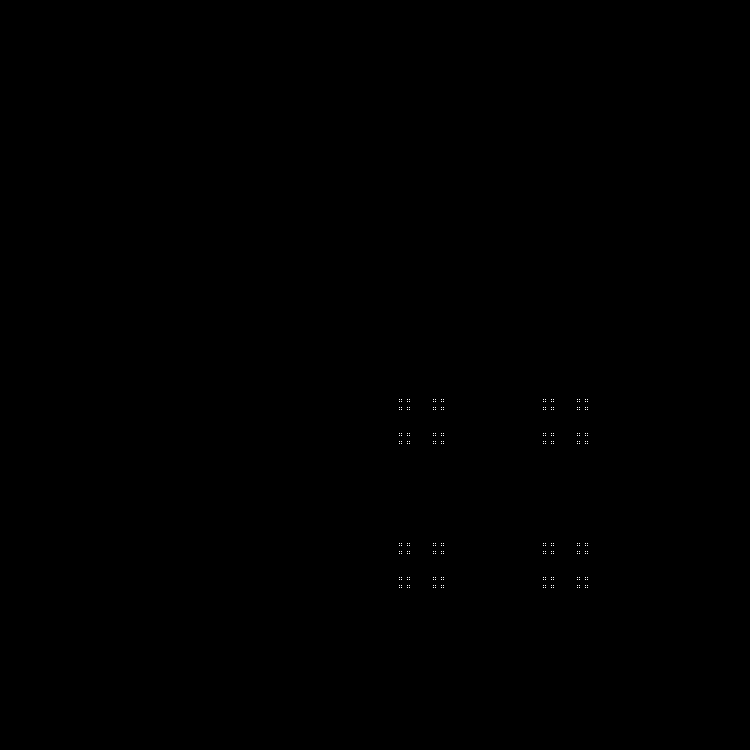
Еще одна последовательность в завершение:

$Q_n=\lfloor n^{2}\sqrt{2} \rfloor \; (\textrm{mod} \; 2); \quad n=0,1,2,…$



Паттерн:



RGB:



Средний слой:



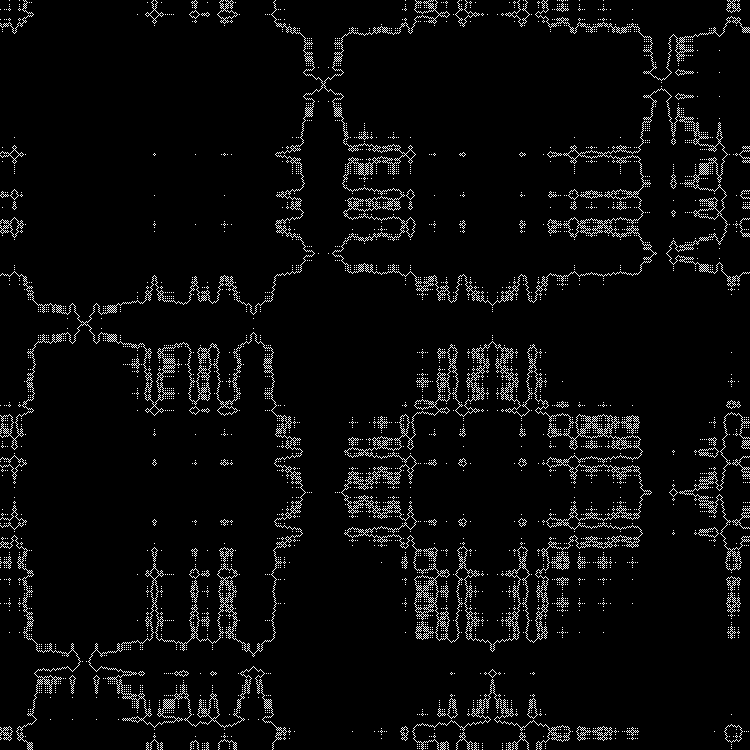
В динамике:



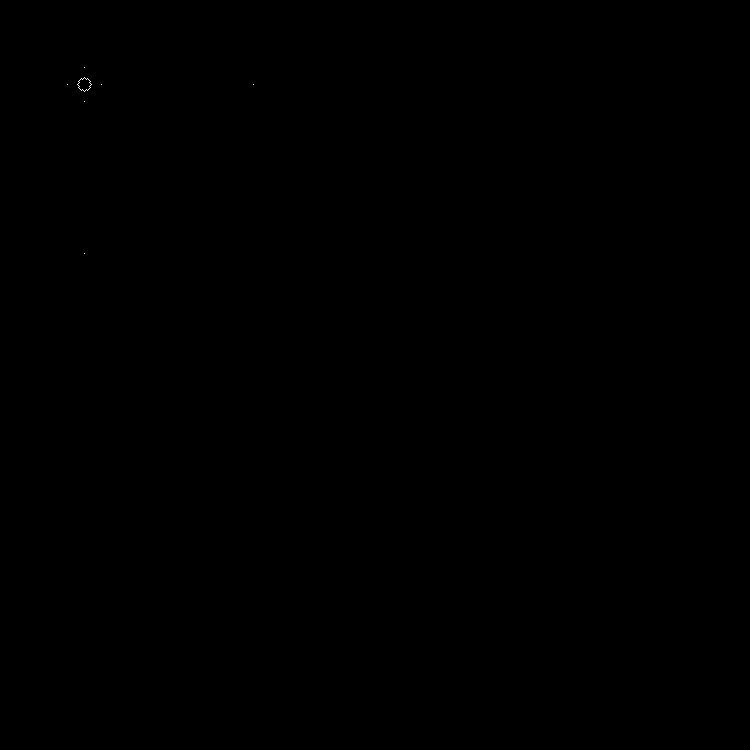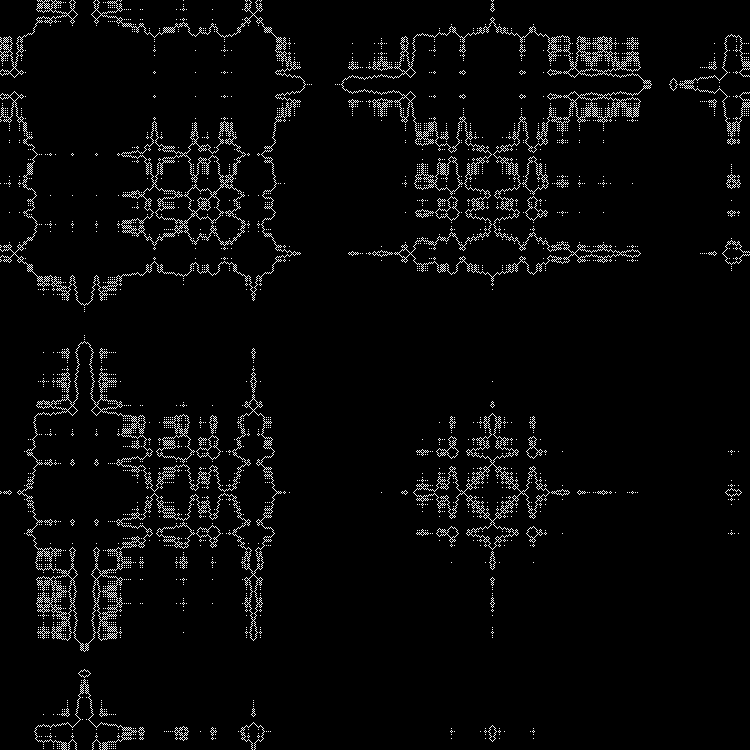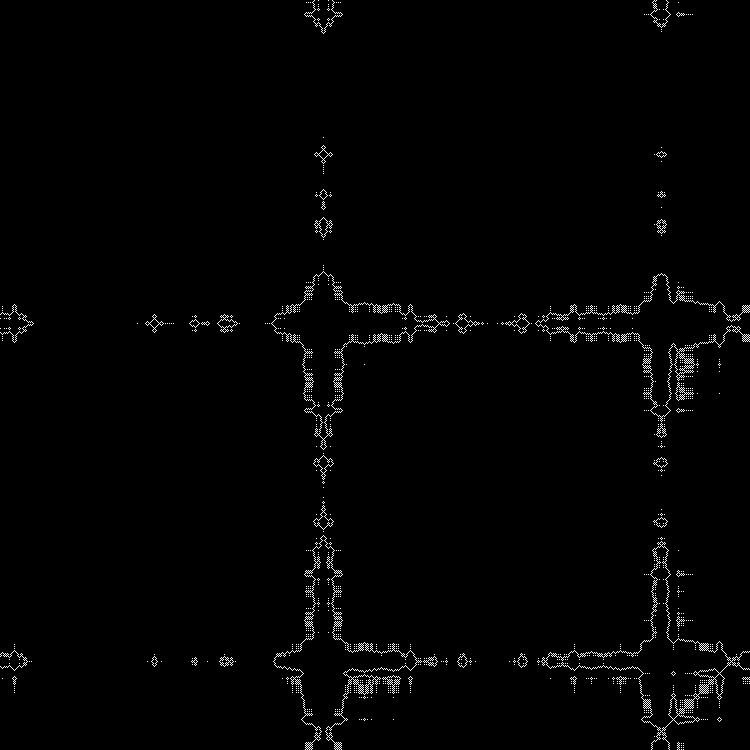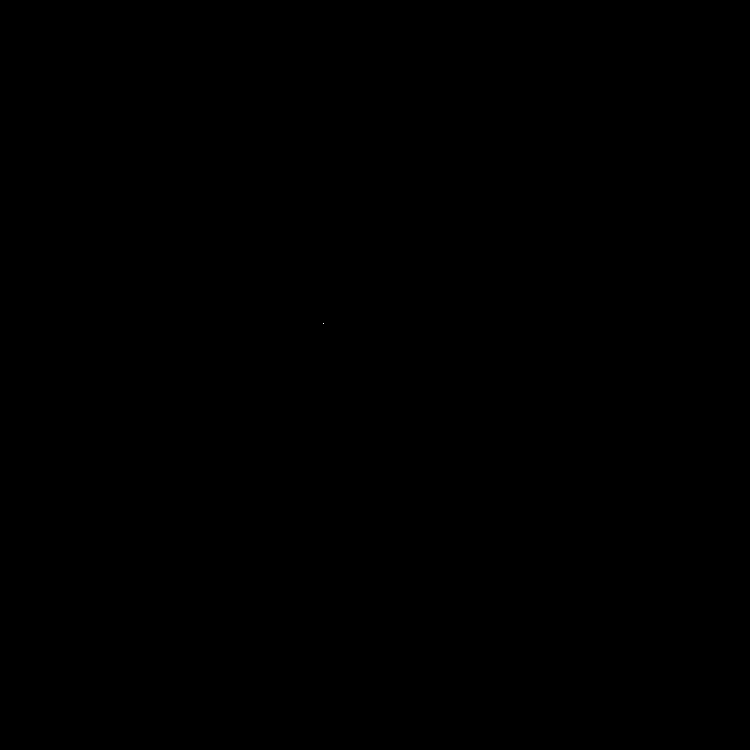
Другие квадратные корни можно вбить в скрипт. (Можно вбивать дробные значения).

Во втором скрипте можно вбить последовательность вручную.

Еще один скрипт для бильярдов. Координаты мышки — размеры бильярда. Паттерн в левой части формируется из последовательности, полученной с помощью остатков от деления (подробности в предыдущей статье). В правой части — четность $\lfloor n\frac{y}{x}\rfloor$.

Комментарии (17)


  1. EvokSinister
    11.04.2019 08:16
    #20012708

    Тот момент, когда человек воистину увлечён своим делом. Ваш труд определённо занял кучу времени.

    Фракткальная графика часто применяется при генерации всяческих процедурных ландшафтов в играх, просто различных природных объектов. И потому мне интересно, а какие области применения вот у таких вот фракталов, как у вас? Получившиеся изображения крайне занимательны, но вот так сложно определить область их применения. Ну, кроме приятного времяпрепровождения от их изучения, само собой)


    1. 3DragonV
      11.04.2019 11:29
      #20013550

      Последний представленный фрактал, лично мне напомнил спрайт взрыва из какой-то игры(названия не помню). В целом, на ландшафте применения, как мне кажется, заканчиваются.


      1. usdglander
        11.04.2019 12:14
        #20013802

        (названия не помню)

        Bomberman


      1. berez
        11.04.2019 13:09
        #20014110

        лично мне напомнил спрайт взрыва из какой-то игры(названия не помню).

        Bomberman — там как раз взрывы этаким крестиком расходились.


      1. weird_one_man
        13.04.2019 11:50
        #20023490

        Забавно, я и не задумывался, что спрайты в старых играх делались с помощью фракталов. На ум падает только отрисовка дыма в кс 1.6 на старом ноуте (белые, расходящиеся хлопья)


  1. staticmain
    11.04.2019 08:48
    #20012796

    А если использовать Pi?


    1. xcont Автор
      11.04.2019 13:13
      #20014128

      n*Pi:



      n*e (число Эйлера):


      1. staticmain
        11.04.2019 13:37
        #20014306

        Можно ли зная свойства фракталов экстраполировать изображение чтобы получить изначальную последовательность, но в расширенном виде?
        Пример: на вход дали 4,8,15,16,23,42, увидели что на изображении часть общеизвестного фрактала, расширили изображение (потому что мы знаем, *как* он должен выглядеть), смотрим выходную последовательность, видим, что 4,8,15,16,23,42 превратилось в 4,8,15,16,23,42,54,90


        1. xcont Автор
          11.04.2019 18:30
          #20016034

          Можно. На вход даем двоичную последовательность. Эту последовательность можно составить комбинаторно — копируя, инвертируя и переставляя биты. На бильярдах это легко показать, но это тема для отдельной статьи.

          Например, последовательность floor(n(sqrt(5)+1)%2, для n=1, 2, 3, ...:
          10100101101001011010110100101101001010010110100101101011010010110100101…

          Можно строить рекурсивно, не вычисляя квадратные корни и остатки от деления:

          function invers(array){ //инвертируем биты
	var temp=[];
	var size=array.length;
	for(var i=0; i<size; i++){
		if(array[i]==0)
			temp[i]=1;
		else
			temp[i]=0;
	}
	return temp;
}
function revers(array, s){ //берем последние s бит в обратном порядке
	var temp=[];
	var size=array.length;
	for(var i=0; i<s; i++) temp[i]=array[size-i-1];
	return temp;
}
function seqence(fn, fn1){ //fn и fn1 - числа Фибоначчи F(n) и F(n-1)
	if(fn1==3) return [1];
	fn1=fn-fn1;
	fn=fn-fn1;
	var array=seqence(fn, fn1); //рекурсия
	var a0=invers(array); //инвертированные биты
	var a1=[];
	if(fn1%2==0) a1=[1]; //добавляем "1" бит, если F(n-1) четное
	var a2=revers(array, Math.floor((fn-fn1)/2)); //биты в обратном порядке
	return a0.concat(a1, a2);
}
console.log((seqence(610, 377)).join(''));


  1. usdglander
    11.04.2019 09:20
    #20012924

    Забота о читателе очень импонирует! Спасибо!


  1. neyrowebster
    11.04.2019 17:30
    #20015666

    Очень круто, зашёл посмотреть на картинки которые заставляют мозг думать что я сошёл с ума.


  1. TwistedFrog
    11.04.2019 17:42
    #20015772

    Да, как тут уже кто-то написал, конечно хотелось бы узнать побольше о практическом применении всех этих интересных фракталов.


    1. Refridgerator
      11.04.2019 17:53
      #20015840

      Получать эстетическое наслаждение от их просмотра — вполне себе практическое применение.


      1. TwistedFrog
        12.04.2019 17:12
        #20021158

        Неужели за это платят зарплату? :)


        1. Vinchi
          13.04.2019 03:02
          #20022950

          Ну можно сделать бакграунд на сайте например


  1. Vinchi
    13.04.2019 03:02
    #20022948

    Эх, гифки надо было в цветном варианте наверно делать


    1. xcont Автор
      13.04.2019 10:29
      #20023332

      Тогда припадок может случиться не только у эпилептиков.
      Два варианта сделал:
      1. Цвет движется вместе со слоем.
      2. Цвет каждого соответствующего слоя не меняется.



      Заголовок спойлера