Статья является продолжением моей первой статьи «Фракталы в простых числах».

В предыдущей статье мы научились рисовать самоподобные паттерны с помощью взаимно простых чисел. В этой статье покажу фрактальную природу числа .
Без предисловия. Под кат.
Определимся с терминологией и обозначениями. В математике, описанные ниже системы называют бильярдами. Далее будем использовать этот термин. Размеры прямоугольного бильярда будем обозначать через (ширина) и (высота).
В предыдущей статье мы брали прямоугольный бильярд со сторонами и , запускали в него шар и отмечали траекторию пунктирной линией через клетку:
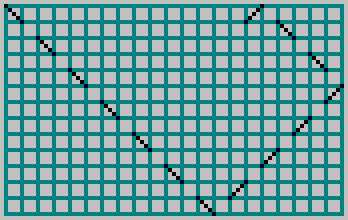
Для взаимно простых и получаем паттерн:

В двоичной версии, траекторию отмечаем не пунктирной линией, а закрашивая поочередно клетки, черным и белым цветом (формируем двоичный массив, в соответствующую ячейку помещаем 0 для черного и 1 для белого):

Правила отражений на границах:
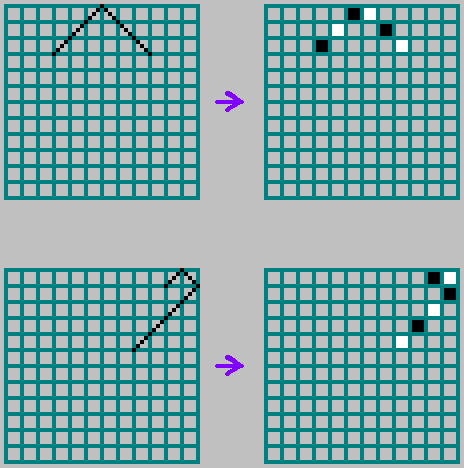
Для взаимно простых и траектория проходит через каждую клетку:

Если стороны имеют общий делитель — тогда шар попадает в угол до того, как пройдет через каждую клетку:

Этот случай удобно рассматривать, как бильярд в прямоугольнике со сторонами и (НОД — наибольший общий делитель):

Прежде чем двигаться дальше, заполним таблицу предложенную пользователем Captain1312 в его статье (стороны бильярда будем делить на НОД).
Для каждого бильярда и возьмем бит с координатами .
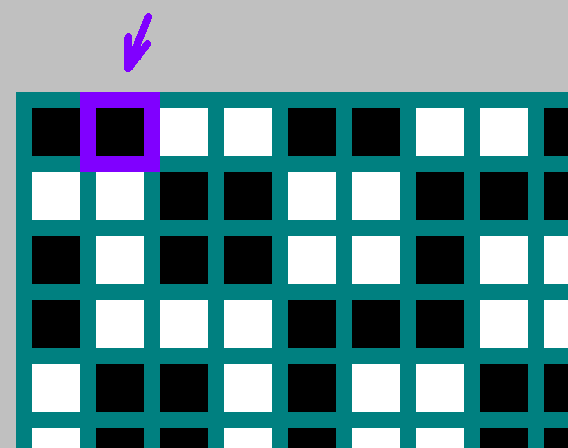
Если является делителем — тогда бит с координатами отсутствует (). В этом случае берем инвертированный бит с координатами .
Заполняем таблицу. Начало координат — левый верхний угол. По — ширина бильярда , по — высота . Для каждого бильярда отмечаем бит , или инвертированный бит (к этой теме вернемся ниже).

Почему мы инвертировали бит в тех случаях, когда ширина бильярда ? Для взаимно простых и , траектория шара проходит через каждую клетку. Между верхней и левой стенкой бильярда, шар каждый раз проходит четное количество клеток.


Биты в левом столбце — инвертированные биты из верхней строки. Нулевой бит не берем — с него начинается траектория:
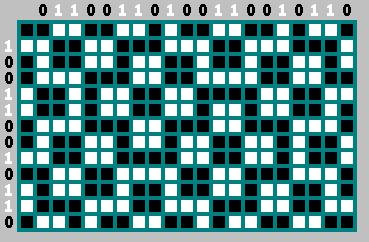
Кроме того, мы можем смело выкинуть каждый второй бит из этой последовательности (бит — инвертированный бит ):

Получили последовательность для бильярда . Последовательность уникальная для каждого и .
Какую бы высоту мы не взяли — шар всегда проходит траекторию между двумя отражениями от верхней стенки. От верхней стенки, движение всегда начинаем с «0» бита (черная клетка) и заканчиваем «1» битом (белая клетка):
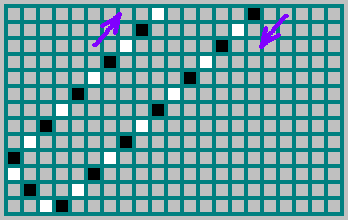
Фактически, последовательность (которую мы выделили выше — ) показывает, с какой стороны прилетел шар: 1 — если шар прилетел, отразившись от правой стенки и 0 — если шар прилетел, отразившись от левой стенки. На картинке траектория шара отмечена черным, если шар двигался вправо и белым — если двигался влево:

Эта последовательность () содержит всю необходимую информацию о паттерне. С помощью нее мы можем восстановить исходный паттерн (и даже заглянуть за нижнюю границу паттерна). Возьмем квадрат со сторонами . Расставим биты нашей последовательности в тех местах, в которых шар ударился об верхнюю стенку (расстояние между соседними касаниями шара — 2 клетки).

Если соответсвующий бит = 1 — начинаем двигаться влево, отмечая траекторию через клетку. Если бит = 0 — двигаемся вправо.
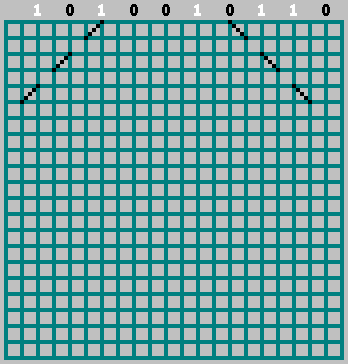
При этом не забываем про нулевой бит:
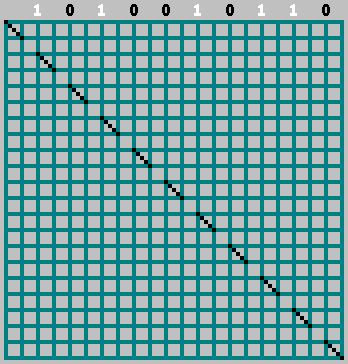
Gif:
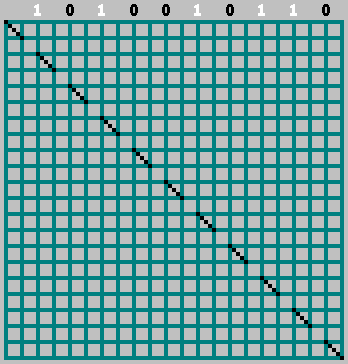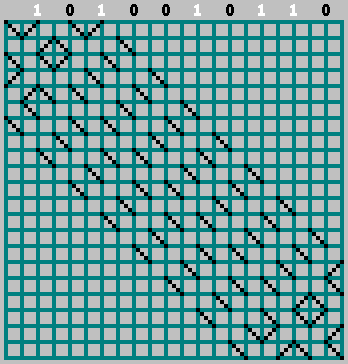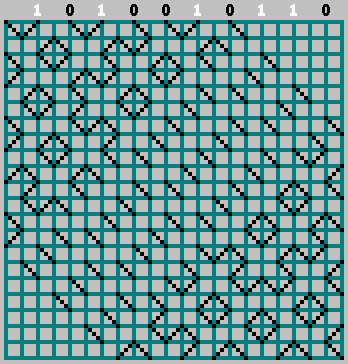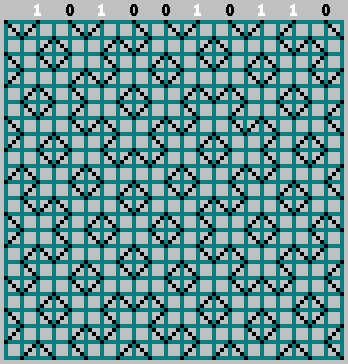
Получили исходный паттерн (и немного заглянули за нижнюю границу):

Скрипт для визуализации двоичных последовательностей
Эту последовательность мы можем построить с помощью остатков от деления.
На числовой оси возьмем две точки: и .

Двигаясь от одной точки к другой, отмеряем расстояния :
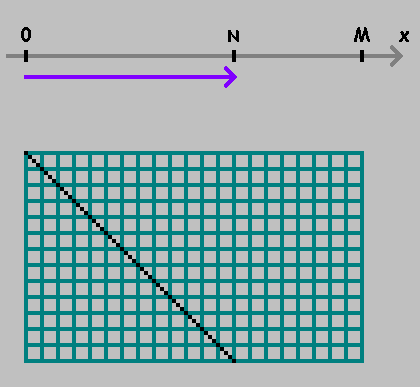
Отметили точку. Продолжаем отмерять расстояние от этой точки, сохраняя направление. Если достигли точки или — меняем направление:
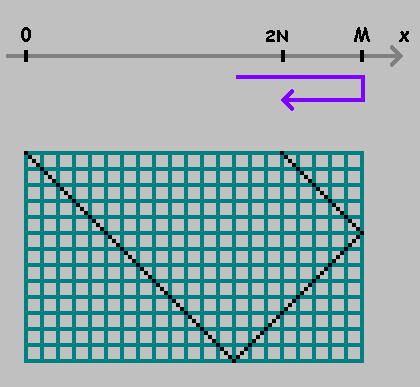
Как видно на рисунках выше, первая точка показывает место, где шар касается нижней стенки бильярда. Эта точка нас не интересует. Мы будем фиксировать только точки для .
Как отметить эти точки? Развернем наш бильярд на оси . Отметим точки . Теперь достигнув точки мы не меняем направление движения, а продолжаем двигаться к точке .
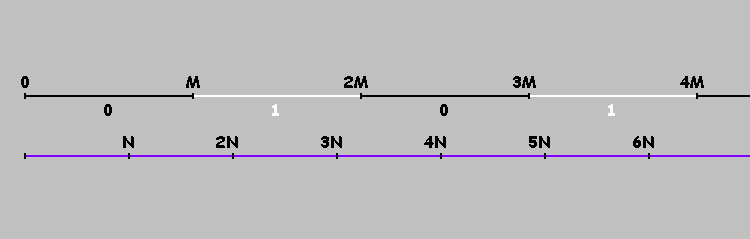
Точки, кратные , делят нашу ось на отрезки. Условно отметим эти отрезки единицами и нулями (чередуются). На отрезках, отмеченных нулями, шар (в прямоугольном бильярде) двигается слева направо. На отрезках, отмеченных единицами — справа налево. Или проще: шар двигается слева направо, если , для
(На эту формулу следует обратить особое внимание. Далее мы к ней вернемся)
Легко заметить, что точка, в которой шар коснулся верхней стенки бильярда — это остаток от деления на . При этом мы можем не фиксировать движение шара в обратную сторону. Берем целую часть от деления на , если она четная — считаем остаток от деления на . Получившийся остаток разделим на 2 (расстояние между соседними точками касания — две клетки). Получили индексы элементов массива, которые нам надо заполнить нулями. Оставшиеся элементы заполняем единицами (шар двигался от правой стенки к левой).
Длина последовательность = .
Теперь мы можем построить двоичную последовательность для бильярда с любыми сторонами и (натуральными числами).
Несколько примеров:
144x89 (числа Фибоначчи):
169x70 (числа Пелля):
233x55 (нечетные числа Фибоначчи и ):
Последовательности у нас есть. Как еще можно визуализировать двоичные последовательности? С помощью Черепашьей графики.
Рисуем отрезок. Далее берем поочередно биты из нашей последовательности. Если бит =1 — поворачиваем отрезок относительно предыдущего на (по часовой). Если бит = 0 — поворачиваем отрезок на . Начало следующего отрезка — конец предыдущего.
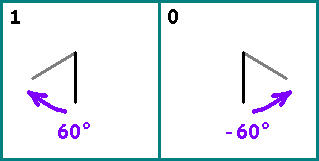
Возьмем два достаточно больших числа Фибоначчи: и .
Построили последовательность:
00101101001011010010100101101001011010110100101101001010010110100101… (257114 символов плюс нулевой бит).
Визуализируем с помощью черепашьей графики. Размер начального отрезка — 10 пикселей (начальный отрезок в правом нижнем углу):

Размер начального отрезка — 5 пикселей:

Размер начального отрезка — 1 пиксель:

Следующий пример — числа Пелля.
Берем и .
Последовательность:
00101001010110101001010110101001010010101101010010101101010010101101 (235415 символов плюс нулевой бит).
Размер начального отрезка — 1 пиксель:
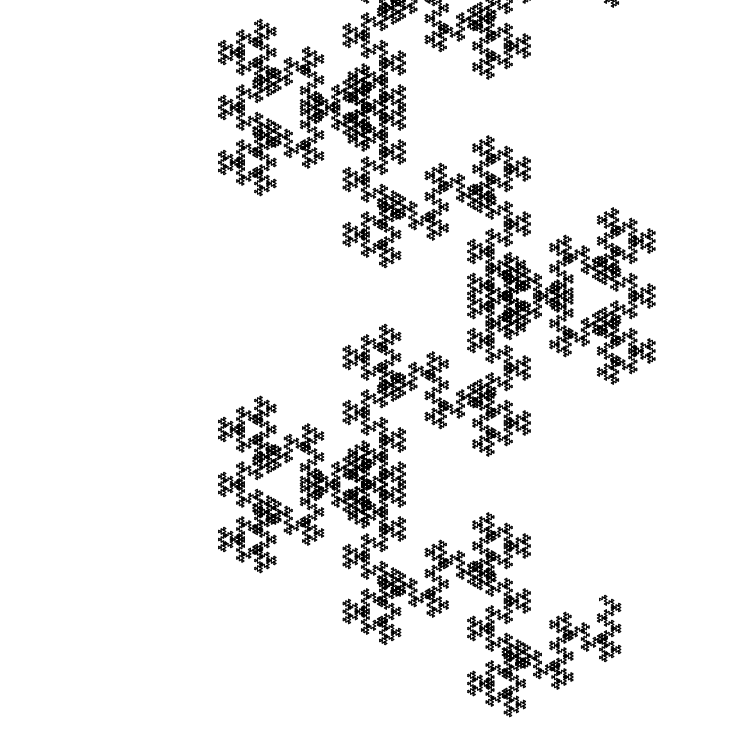
Еще один пример — нечетные числа Фибоначчи и .
Берем и .
Последовательность:
00110110010010011011001001001101101100100110110110010011011011001001… (158905 плюс нулевой бит).
Вместо углов и будем использовать углы и .
Размер начального отрезка — 5 пикселей:

Размер начального отрезка — 0.4 пикселя:

У этой кривой есть название — «Fibonacci word fractal». Размерность Хаусдорфа для этой кривой известна:
Скрипт для визуализации двоичных последовательностей с помощью Turtle Graphics
Можно ли нарисовать паттерн для бильярда, стороны которого несоизмеримы (одна из сторон — иррациональное число)? Задача нетривиальная. Пытаясь решить эту задачу, мы столкнемся с рядом вопросов:
1. Если стороны несоизмеримы — мы не можем замостить бильярд клетками одинаковой величины.
2. Если стороны несоизмеримы — шар будет бесконечно отражаться и никогда не попадет в угол.
3. Последовательности в бильярдах заполняются не по порядку, а хаотично.

Первые два вопроса, очевидно, не имеют решения. Но если бы существовал способ заполнить последовательность по порядку — тогда мы могли бы, двигаясь по последовательности слева направо, восстановить паттерн способом, которым мы пользовались выше. И тем самым увидеть, как выглядит паттерн в левом верхнем углу бильярда, стороны которого несоизмеримы.
Возьмем бильярд, стороны которого равны числам Фибоначчи (с другими числами такой фокус может не сработать). Запустим в него шар и будем фиксировать номер касания шара у верхней стенки. Номера закрасим белым цветом — если шар двигался справа налево и черным — если шар двигался слева направо:

Белому цвету соответствует единица в последовательности, черному — ноль. Теперь расставим номера по порядку:

Получили точно такую же последовательность единиц и нулей.
Фактически, в некоторых случаях, нам не надо брать остаток от деления. Для чисел Фибоначчи достаточно проверить четность целой части от деления на :
В числителе у нас . В знаменателе — .
Как известно:
— Золотое сечение. Иррациональное число. Теперь нашу формулу можем записать как:
Получили формулу, с помощью которой можем по порядку заполнять последовательность для бильярда, ширина которого равна , а высота — . Длина последовательности = , но мы можем восстанавливать часть паттерна, двигаясь слева направо по последовательности и заглянуть в верхний левый угол бильярда. Осталось разобраться, как посчитать
Единицу деленную на золотое сечение можно переписать как:
Мы можем избавиться от двойки:
Наша формула принимает вид:
Для наглядности нарисовал таблицу. В третьей колонке отбрасываем дробную часть и оставляем целую. В четвертой колонке проверяем четность целой части:
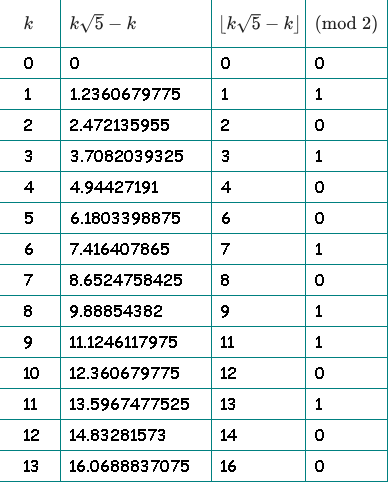
В четвертой колонке получили нашу последовательность: 01010010110100…
Продолжаем вычислять биты для остальных . Восстанавливаем часть паттерна для бильярда со сторонами и :

Если не отнимать каждый раз — тогда каждый второй бит в последовательности инвертируются. Получим общую формулу:
Что нам мешает вместо квадратного корня из пяти использовать квадратный корень из трех или, скажем, из двух? Ничего.
Построим последовательность для
Первые несколько бит последовательности:
00100101101001001011010010110110100101101001001011010010010110100101…
Визуализировать будем с помощью черепашьей графики. Углы 90 и -90 градусов. Размер начального отрезка 5 пикселей:

Размер начального отрезка — 0.5 пикселя:

Построим последовательность для
Первые несколько бит последовательности (A083035):
01001101100100110010011011001101100100110110011011001001100100110110…
Углы 90 и -90 градусов. Размер начального отрезка 5 пикселей:

Размер начального отрезка — 0.5 пикселя:

Углы 60 и -60 градусов. Размер начального отрезка 5 пикселей:

Скрипт для визуализации
Кто-то может засомневаться в том, что четность целой части от дает фрактальную последовательность. Визуализируем часть этой последовательности вторым способом:

Для наглядности, закрасил самую длинную кривую в получившемся паттерне:

У этой кривой есть название — «Fibonacci word fractal».
Как с помощью бильярда получить эту последовательность? Берем бильярд, ширина которого = 1, а высота = . У верхней и нижней границы фиксируем направление движения шара. Если шар двигался слева направо — записываем 0, если справа налево — записываем 1.

Два графика:


Продолжать в том же духе можно очень долго — у паттернов есть много интересных свойств. Но статья и без того получилась слишком громоздкой. Об одном из интересных свойств расскажу напоследок.

В предыдущей статье мы научились рисовать самоподобные паттерны с помощью взаимно простых чисел. В этой статье покажу фрактальную природу числа .
Без предисловия. Под кат.
Определимся с терминологией и обозначениями. В математике, описанные ниже системы называют бильярдами. Далее будем использовать этот термин. Размеры прямоугольного бильярда будем обозначать через (ширина) и (высота).
Двоичный бильярд
В предыдущей статье мы брали прямоугольный бильярд со сторонами и , запускали в него шар и отмечали траекторию пунктирной линией через клетку:

Для взаимно простых и получаем паттерн:

В двоичной версии, траекторию отмечаем не пунктирной линией, а закрашивая поочередно клетки, черным и белым цветом (формируем двоичный массив, в соответствующую ячейку помещаем 0 для черного и 1 для белого):

Правила отражений на границах:

Для взаимно простых и траектория проходит через каждую клетку:

Для разных M и N
Больше всего в этих паттернах удивляет то, что для разных и получается свой уникальный паттерн:





В статье, в качестве и , мы используем преимущественно числа Фибоначчи. Здесь можно нарисовать паттерны для других чисел (координат мышки).





В статье, в качестве и , мы используем преимущественно числа Фибоначчи. Здесь можно нарисовать паттерны для других чисел (координат мышки).
Если стороны имеют общий делитель — тогда шар попадает в угол до того, как пройдет через каждую клетку:

Этот случай удобно рассматривать, как бильярд в прямоугольнике со сторонами и (НОД — наибольший общий делитель):

Прежде чем двигаться дальше, заполним таблицу предложенную пользователем Captain1312 в его статье (стороны бильярда будем делить на НОД).
бит
Для каждого бильярда и возьмем бит с координатами .

Если является делителем — тогда бит с координатами отсутствует (). В этом случае берем инвертированный бит с координатами .
Заполняем таблицу. Начало координат — левый верхний угол. По — ширина бильярда , по — высота . Для каждого бильярда отмечаем бит , или инвертированный бит (к этой теме вернемся ниже).

Немного о числах Фибоначчи
На таблице видны линии, выходящие из левого верхнего угла. Если построить такую таблицу для бита с координатами — эти линии видно еще лучше:

Есть еще один оригинальный способ получить эти линии.
Для каждого и , если является делителем , построим последовательность чисел Фибоначчи:
И отметим на графике точки и :


Есть еще один оригинальный способ получить эти линии.
Для каждого и , если является делителем , построим последовательность чисел Фибоначчи:
И отметим на графике точки и :

Двоичная последовательность
Почему мы инвертировали бит в тех случаях, когда ширина бильярда ? Для взаимно простых и , траектория шара проходит через каждую клетку. Между верхней и левой стенкой бильярда, шар каждый раз проходит четное количество клеток.


Биты в левом столбце — инвертированные биты из верхней строки. Нулевой бит не берем — с него начинается траектория:

Кроме того, мы можем смело выкинуть каждый второй бит из этой последовательности (бит — инвертированный бит ):

Получили последовательность для бильярда . Последовательность уникальная для каждого и .
Какую бы высоту мы не взяли — шар всегда проходит траекторию между двумя отражениями от верхней стенки. От верхней стенки, движение всегда начинаем с «0» бита (черная клетка) и заканчиваем «1» битом (белая клетка):

Фактически, последовательность (которую мы выделили выше — ) показывает, с какой стороны прилетел шар: 1 — если шар прилетел, отразившись от правой стенки и 0 — если шар прилетел, отразившись от левой стенки. На картинке траектория шара отмечена черным, если шар двигался вправо и белым — если двигался влево:

Это интересно
С помощью бильярда можно делить два числа в двоичной системе счисления. В момент касания верхней или нижней стенки фиксируем направление движения шара. Если шар двигался вправо — запишем 0. Если влево — запишем 1. Фиксировать будем каждое касание шара.
Первое касание нижней стенки. Шар двигался вправо. Зафиксировали 0
Второе касание — верхней стенки. Шар двигался влево. Зафиксировали 1
Четвертое касание — верхней стенки. Шар двигался вправо. Зафиксировали 0
Восьмое касание — верхней стенки. Шар двигался вправо. Зафиксировали 0
И т.д.
Получили: 0.1001111001111001111… — это двоичная запись дроби .

Первое касание нижней стенки. Шар двигался вправо. Зафиксировали 0
Второе касание — верхней стенки. Шар двигался влево. Зафиксировали 1
Четвертое касание — верхней стенки. Шар двигался вправо. Зафиксировали 0
Восьмое касание — верхней стенки. Шар двигался вправо. Зафиксировали 0
И т.д.
Получили: 0.1001111001111001111… — это двоичная запись дроби .

Эта последовательность () содержит всю необходимую информацию о паттерне. С помощью нее мы можем восстановить исходный паттерн (и даже заглянуть за нижнюю границу паттерна). Возьмем квадрат со сторонами . Расставим биты нашей последовательности в тех местах, в которых шар ударился об верхнюю стенку (расстояние между соседними касаниями шара — 2 клетки).

Если соответсвующий бит = 1 — начинаем двигаться влево, отмечая траекторию через клетку. Если бит = 0 — двигаемся вправо.

При этом не забываем про нулевой бит:

Gif:

Получили исходный паттерн (и немного заглянули за нижнюю границу):

Скрипт для визуализации двоичных последовательностей
Эту последовательность мы можем построить с помощью остатков от деления.
Одномерный бильярд
На числовой оси возьмем две точки: и .

Двигаясь от одной точки к другой, отмеряем расстояния :

Отметили точку. Продолжаем отмерять расстояние от этой точки, сохраняя направление. Если достигли точки или — меняем направление:

Как видно на рисунках выше, первая точка показывает место, где шар касается нижней стенки бильярда. Эта точка нас не интересует. Мы будем фиксировать только точки для .
Как отметить эти точки? Развернем наш бильярд на оси . Отметим точки . Теперь достигнув точки мы не меняем направление движения, а продолжаем двигаться к точке .

Точки, кратные , делят нашу ось на отрезки. Условно отметим эти отрезки единицами и нулями (чередуются). На отрезках, отмеченных нулями, шар (в прямоугольном бильярде) двигается слева направо. На отрезках, отмеченных единицами — справа налево. Или проще: шар двигается слева направо, если , для
(На эту формулу следует обратить особое внимание. Далее мы к ней вернемся)
Легко заметить, что точка, в которой шар коснулся верхней стенки бильярда — это остаток от деления на . При этом мы можем не фиксировать движение шара в обратную сторону. Берем целую часть от деления на , если она четная — считаем остаток от деления на . Получившийся остаток разделим на 2 (расстояние между соседними точками касания — две клетки). Получили индексы элементов массива, которые нам надо заполнить нулями. Оставшиеся элементы заполняем единицами (шар двигался от правой стенки к левой).
Длина последовательность = .
function sequence(m,n){
var md=m/2;
var array=[];
for(var k=0;k<md;k++) array[k]=1;
for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0;
return array;
}
console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001Теперь мы можем построить двоичную последовательность для бильярда с любыми сторонами и (натуральными числами).
Несколько примеров:
144x89 (числа Фибоначчи):
010100101101001011010110100101101001010010110100101101011010010110100101169x70 (числа Пелля):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010233x55 (нечетные числа Фибоначчи и ):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100Еще одна интересная таблица
Очень любопытные графики получаются, если взять бильярд с шириной и построить последовательности для каждого от до . Далее эти последовательности сложить стопкой.
Несколько примеров.
M=610:

M=611:

M=612:

M=613:

M=614:

Для остальных M
var array;
for(var y=1;y<m;y++){
array=sequence(m,y);
for(var x=0;x<array.length;x++){
if(array[x]==0) context.fillRect (x, y, 1, 1);
}
}
Несколько примеров.
M=610:

M=611:

M=612:

M=613:

M=614:

Для остальных M
Последовательности у нас есть. Как еще можно визуализировать двоичные последовательности? С помощью Черепашьей графики.
Turtle graphics
Рисуем отрезок. Далее берем поочередно биты из нашей последовательности. Если бит =1 — поворачиваем отрезок относительно предыдущего на (по часовой). Если бит = 0 — поворачиваем отрезок на . Начало следующего отрезка — конец предыдущего.

Возьмем два достаточно больших числа Фибоначчи: и .
Построили последовательность:
00101101001011010010100101101001011010110100101101001010010110100101… (257114 символов плюс нулевой бит).
Визуализируем с помощью черепашьей графики. Размер начального отрезка — 10 пикселей (начальный отрезок в правом нижнем углу):

Размер начального отрезка — 5 пикселей:

Размер начального отрезка — 1 пиксель:

Следующий пример — числа Пелля.
Берем и .
Последовательность:
00101001010110101001010110101001010010101101010010101101010010101101 (235415 символов плюс нулевой бит).
Размер начального отрезка — 1 пиксель:
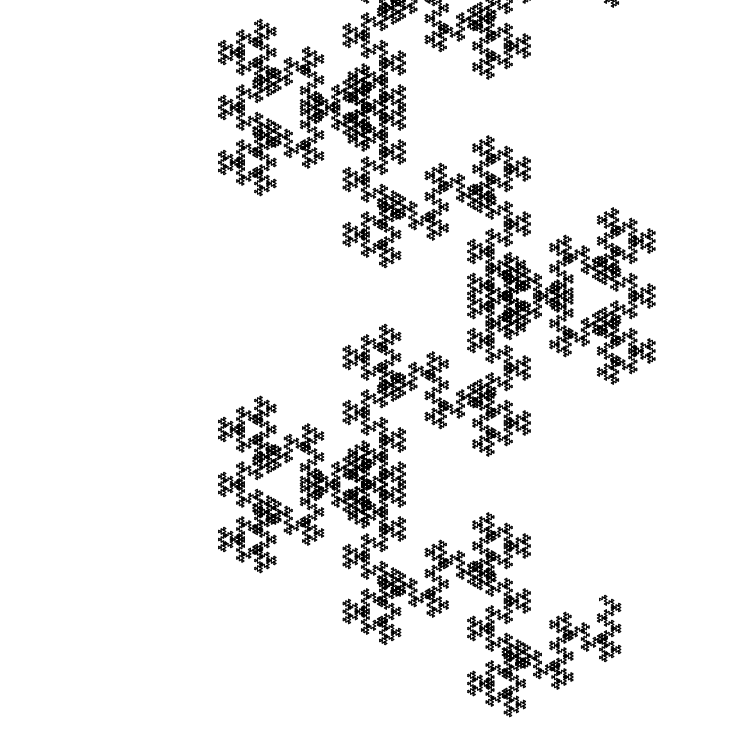
Еще один пример — нечетные числа Фибоначчи и .
Берем и .
Последовательность:
00110110010010011011001001001101101100100110110110010011011011001001… (158905 плюс нулевой бит).
Вместо углов и будем использовать углы и .
Размер начального отрезка — 5 пикселей:

Размер начального отрезка — 0.4 пикселя:

У этой кривой есть название — «Fibonacci word fractal». Размерность Хаусдорфа для этой кривой известна:
Скрипт для визуализации двоичных последовательностей с помощью Turtle Graphics
Проблема
Можно ли нарисовать паттерн для бильярда, стороны которого несоизмеримы (одна из сторон — иррациональное число)? Задача нетривиальная. Пытаясь решить эту задачу, мы столкнемся с рядом вопросов:
1. Если стороны несоизмеримы — мы не можем замостить бильярд клетками одинаковой величины.
2. Если стороны несоизмеримы — шар будет бесконечно отражаться и никогда не попадет в угол.
3. Последовательности в бильярдах заполняются не по порядку, а хаотично.

Первые два вопроса, очевидно, не имеют решения. Но если бы существовал способ заполнить последовательность по порядку — тогда мы могли бы, двигаясь по последовательности слева направо, восстановить паттерн способом, которым мы пользовались выше. И тем самым увидеть, как выглядит паттерн в левом верхнем углу бильярда, стороны которого несоизмеримы.
Черная магия
Возьмем бильярд, стороны которого равны числам Фибоначчи (с другими числами такой фокус может не сработать). Запустим в него шар и будем фиксировать номер касания шара у верхней стенки. Номера закрасим белым цветом — если шар двигался справа налево и черным — если шар двигался слева направо:

Белому цвету соответствует единица в последовательности, черному — ноль. Теперь расставим номера по порядку:

Получили точно такую же последовательность единиц и нулей.
Для других чисел
Начало координат — левый верхний угол. По оси — ширина бильярда . По оси — высота бильярда . Белыми точками отмечены числа, для которых последовательности совпадают:

Числа, для которых последовательность инвертируется:

Закинул скрипт:

Первая строка — координаты мышки, которые используются в качестве ширины и высоты бильярда.
Вторая строка — первые 100 бит последовательности, полученной через остатки от деления.
Третья строка — первые 100 бит последовательности, полученной через четность целой части.
Черный цвет — Визуализация первой последовательности с помощью Turtle graphics.
Фиолетовый — визуализация второй последовательности.

Числа, для которых последовательность инвертируется:

Закинул скрипт:

Первая строка — координаты мышки, которые используются в качестве ширины и высоты бильярда.
Вторая строка — первые 100 бит последовательности, полученной через остатки от деления.
Третья строка — первые 100 бит последовательности, полученной через четность целой части.
Черный цвет — Визуализация первой последовательности с помощью Turtle graphics.
Фиолетовый — визуализация второй последовательности.
Фактически, в некоторых случаях, нам не надо брать остаток от деления. Для чисел Фибоначчи достаточно проверить четность целой части от деления на :
В числителе у нас . В знаменателе — .
Как известно:
— Золотое сечение. Иррациональное число. Теперь нашу формулу можем записать как:
Получили формулу, с помощью которой можем по порядку заполнять последовательность для бильярда, ширина которого равна , а высота — . Длина последовательности = , но мы можем восстанавливать часть паттерна, двигаясь слева направо по последовательности и заглянуть в верхний левый угол бильярда. Осталось разобраться, как посчитать
Единицу деленную на золотое сечение можно переписать как:
Мы можем избавиться от двойки:
Наша формула принимает вид:
Для наглядности нарисовал таблицу. В третьей колонке отбрасываем дробную часть и оставляем целую. В четвертой колонке проверяем четность целой части:

В четвертой колонке получили нашу последовательность: 01010010110100…
Продолжаем вычислять биты для остальных . Восстанавливаем часть паттерна для бильярда со сторонами и :

Если не отнимать каждый раз — тогда каждый второй бит в последовательности инвертируются. Получим общую формулу:
Что нам мешает вместо квадратного корня из пяти использовать квадратный корень из трех или, скажем, из двух? Ничего.
Построим последовательность для
var x=3;
var q=[];
for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2;
Первые несколько бит последовательности:
00100101101001001011010010110110100101101001001011010010010110100101…
Визуализировать будем с помощью черепашьей графики. Углы 90 и -90 градусов. Размер начального отрезка 5 пикселей:

Размер начального отрезка — 0.5 пикселя:

Построим последовательность для
var x=2;
var q=[];
for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2;
Первые несколько бит последовательности (A083035):
01001101100100110010011011001101100100110110011011001001100100110110…
Углы 90 и -90 градусов. Размер начального отрезка 5 пикселей:

Размер начального отрезка — 0.5 пикселя:

Это интересно
Из этой кривой можно восстановить «бильярдный паттерн» и посмотреть, что находится вокруг кривой:

Интересно было бы подобрать и для этого паттерна.

Интересно было бы подобрать и для этого паттерна.
И это
Количество отрезков в повторяющейся части кривой = (числа Пелля: 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, … ).


Углы 60 и -60 градусов. Размер начального отрезка 5 пикселей:

Скрипт для визуализации
Кто-то может засомневаться в том, что четность целой части от дает фрактальную последовательность. Визуализируем часть этой последовательности вторым способом:

Для наглядности, закрасил самую длинную кривую в получившемся паттерне:

У этой кривой есть название — «Fibonacci word fractal».
Как с помощью бильярда получить эту последовательность? Берем бильярд, ширина которого = 1, а высота = . У верхней и нижней границы фиксируем направление движения шара. Если шар двигался слева направо — записываем 0, если справа налево — записываем 1.

Два графика:


Продолжать в том же духе можно очень долго — у паттернов есть много интересных свойств. Но статья и без того получилась слишком громоздкой. Об одном из интересных свойств расскажу напоследок.
При просмотре картинок, у некоторых пользователей может случиться эпилептический припадок.
В двоичном бильярде мы запускали шар из левого верхнего угла и заполняли матрицу битами.
Для бильярда 610х377:

Увеличенная часть паттерна:

Если запустить второй шар из другого угла (из левого нижнего для бильярда 610х377) и отметить биты, которые совпадают для обеих траекторий — получим очень любопытный паттерн:

Совпадающие биты отмечены черными пикселями. Увеличенная часть паттерна:

Существует еще два способа нарисовать этот паттерн. Об одном из них упомянул в статье Perfect shuffle. Второй:
Нарисуем график функции:
И отметим черными точками :

Увеличенная часть паттерна:

Для бильярда 610х377:

Увеличенная часть паттерна:

Если запустить второй шар из другого угла (из левого нижнего для бильярда 610х377) и отметить биты, которые совпадают для обеих траекторий — получим очень любопытный паттерн:

Совпадающие биты отмечены черными пикселями. Увеличенная часть паттерна:

Существует еще два способа нарисовать этот паттерн. Об одном из них упомянул в статье Perfect shuffle. Второй:
Нарисуем график функции:
И отметим черными точками :

Увеличенная часть паттерна:



xcont Автор
AEP
Можно было залить на jsfiddle.net или аналоги.
babylon
Это Ваша работа или хобби?
Javian
off Картинка первого графика (y*sqrt(x)) очень похожа на искажения на аналоговом видеосигнале при передаче изображения из прямых линий, выходящих из одной точки.
rumkin
От таких изображений эпилептический припадок может случиться. Лучше убавьте контраст.
xcont Автор
Спрятал «проблемные» картинки под спойлер.
vvzvlad
Ну и зря. Эпиприступ, провоцируемый регулярными узорами — очень большая редкость, нет нужны настолько параноить. Вот если бы там была анимация, другое дело.
S-e-n
Спасибо за статью.
Я не специалист, но не поставить ли тут варнинг для эпилептиков? Я не эпилептик, но от продолжительного созерцания последней картинки слегка поплохело.
amarao
Последняя картинка поста обладает свойством оптической иллюзии — если её скроллить, разные части картинки будут двигаться с разной скоростью.
zuborg
Отправьте ссылку Стивену Вольфраму, он оценит! )
fivehouse
Прикольно. На самом деле свойство образовывать фракталы достаточно распространено в рекуррентных вычислениях.
Но вызовы, например, в том, чтобы попытаться предсказать с какой нибудь степенью уверенности еще не вычисленное изображение.
Или доказать невозможность/сложность решения обратной задачи. То есть при известном способе построения фрактала и наличии части изображения фрактала доказать невозможность/сложность вычисления исходных параметров.
Smith2018
Очень красиво! Только зачем это все нужно? Убили столько времени на то, чтоб сгенерировать всю эту хр*нотень…