Несмотря на развитие науки и техники, сжатие информации по прежнему остаётся одной из актуальных задач, где особое место занимают алгоритмы сжатия видеоинформации. В этой публикации речь пойдёт о сжатии статических цветных изображений JPEG-подобными алгоритмами.
Для начала хочу поблагодарить автора статей «Декодирование JPEG для чайников» и «Изобретаем JPEG», которые очень помогли мне в работе по написанию данной публикации. Когда я занялся вопросами изучения алгоритмов сжатия изображений с потерями, то в части алгоритма JPEG меня всё время мучил вопрос: «Почему роль базисного преобразования в алгоритме JPEG отведена именно частному случаю преобразования Фурье?». Здесь автор даёт ответ на этот вопрос, но я решил подойти к нему не с точки зрения теории, математических моделей или программной реализации, а с точки зрения схемотехники.
Алгоритм сжатия изображений JPEG является алгоритмом цифровой обработки сигналов, которые, аппаратно, как правило, реализуются либо на цифровых сигнальных процессорах, либо на программируемых логических интегральных схемах. В моём случае, выбор для работы цифрового сигнального процессора означал бы приход к тому, от чего я пытался уйти — к программной реализации, поэтому решено было остановиться на программируемой логике.
В одном из интернет-магазинов я приобрёл довольно простую отладочную плату, которая содержит в своём составе ПЛИС Altera FPGA Cyclone 4 -EP4CE6E22 и память SRAM 512Kx8. Так как ПЛИС была фирмы Altera, то и для разработки решено было использовать среду Quartus II Web Edition. Разработка отдельных функциональных блоков аппаратного кодека осуществлялась на языке Verilog, а сборка в единую схему производилась в графическом редакторе среды Quartus II Web Edition.
Для связи с персональным компьютером (приём команд, приём/передача обрабатываемых данных), на языке Verilog мной был написан простенький асинхронный приёмопередатчик UART. Для подключения к COM-порту (RS-232) компьютера, на базе микросхемы MAX3232WE и из того, что было под рукой, наспех, был спаян преобразователь уровней. В итоге вот, что получилось:

Для отправки команд с персонального компьютера, а также приёма-передачи данных использовалась триальная версия программы ADVANCED SERIAL PORT MONITOR, которая позволяет формировать не только отдельные посылки байт данных, но и формировать потоки данных из содержимого файлов, а также записывать принимаемые потоки данных в файл, что позволило передавать и принимать файлы. Никакие протоколы и контрольные суммы, для для приёма/передачи данных по UART я тут не использую и не контролирую (попросту лень было всё это предусматривать и реализовывать), во время связи для приёма/передачи я использовал, что называется, «сырые данные».
Все арифметические операции связанные с дробными числами в кодеке осуществляются в формате с фиксированной точкой, операции сложения и вычитания осуществляются в дополнительном коде, в принципе это и так понятно. Как определялась разрядность обрабатываемых данных будет описано ниже.
Операция сжатия осуществляется над исходными изображениями, представленными в формате .bmp с глубиной цвета — 24 бита на пиксель (по 8 бит на каждую из цветовых компонент).
Имеющаяся на отладочной плате память была организована следующим образом: адреса с 00000h по 3FFFFh (в шестнадцатиричной системе счисления) выделены под хранение исходных данных (рисунок в формате .bmp для сжатия, либо закодированные данные для распаковки), итого 256 КБ, остальные 256 КБ — пространство для записи получаемых, в результате сжатия или распаковки данных, это адреса с 40000h по 7FFFFh. Я думаю, очевидно, что максимальный размер сжимаемых изображений ограничен объёмом, выделяемой для хранения данных, памяти.
Алгоритм работы устройства такой: сразу после подачи питания кодек ожидает поток данных по UART, любые принятые, при этом, данные здесь интерпретируются как исходный файл для обработки, если пауза между байтами составляет 10 мс, то это интерпретируется как конец файла, и следующий за паузой байт, принимаемый по UART, воспринимаются устройством как команда. Команды представляют собой конкретные значения байт. Например, после приёма файла через 10 мс, поступившее в кодек по UART, значение байта AAh интерпретируется устройством как команда, по которой происходит выдача по UART на компьютер данных с микросхемы памяти, начиная с адреса 40000h и до значения адреса на котором завершилась запись обработанных данных, т.е. на компьютер передаются результаты сжатия/распаковки. Значение EEh интерпретируется как команда на сжатие/распаковку изображения, также для отладки мной был предусмотрен ряд других команд.
Что касается структуры файла с жатым изображением, то тут я решил не заморачиваться, и, в отличии от алгоритма JPEG, реализуемый мной алгоритм, носит довольно-таки узконаправленный характер и не рассчитан на все случаи жизни, поэтому получаемые, в результате сжатия, данные единым потоком записываются в выделенную область памяти. Единственное, что тут нужно отметить, для того чтобы не реализовывать генератор заголовка .bmp файла (тоже было лень), при сжатии он просто целиком переписывается в начальную (с адреса 40000h) область памяти, отведённую для конечных данных, а затем уже, начиная со смещения, с которого в исходном .bmp файле хранятся пиксельные данные, записываются сжатые данные. Это смещение храниться в заголовке .bmp файла по адресу 0Ah относительно его начала, и, как правило составляет 36h. При распаковке, соответственно осуществляется такая же операция.
Итак, сжатие изображений JPEG-подобными алгоритмами осуществляется в следующей последовательности:
Распаковка идёт в обратном порядке.
Из всех, вышеперечисленных этапов, в кодеке я не реализовывал субдискретизацию, так как посчитал её лишней (может быть я не прав).
Исходя из представленной выше последовательности действий, мной была разработана следующая функциональная схема кодека:
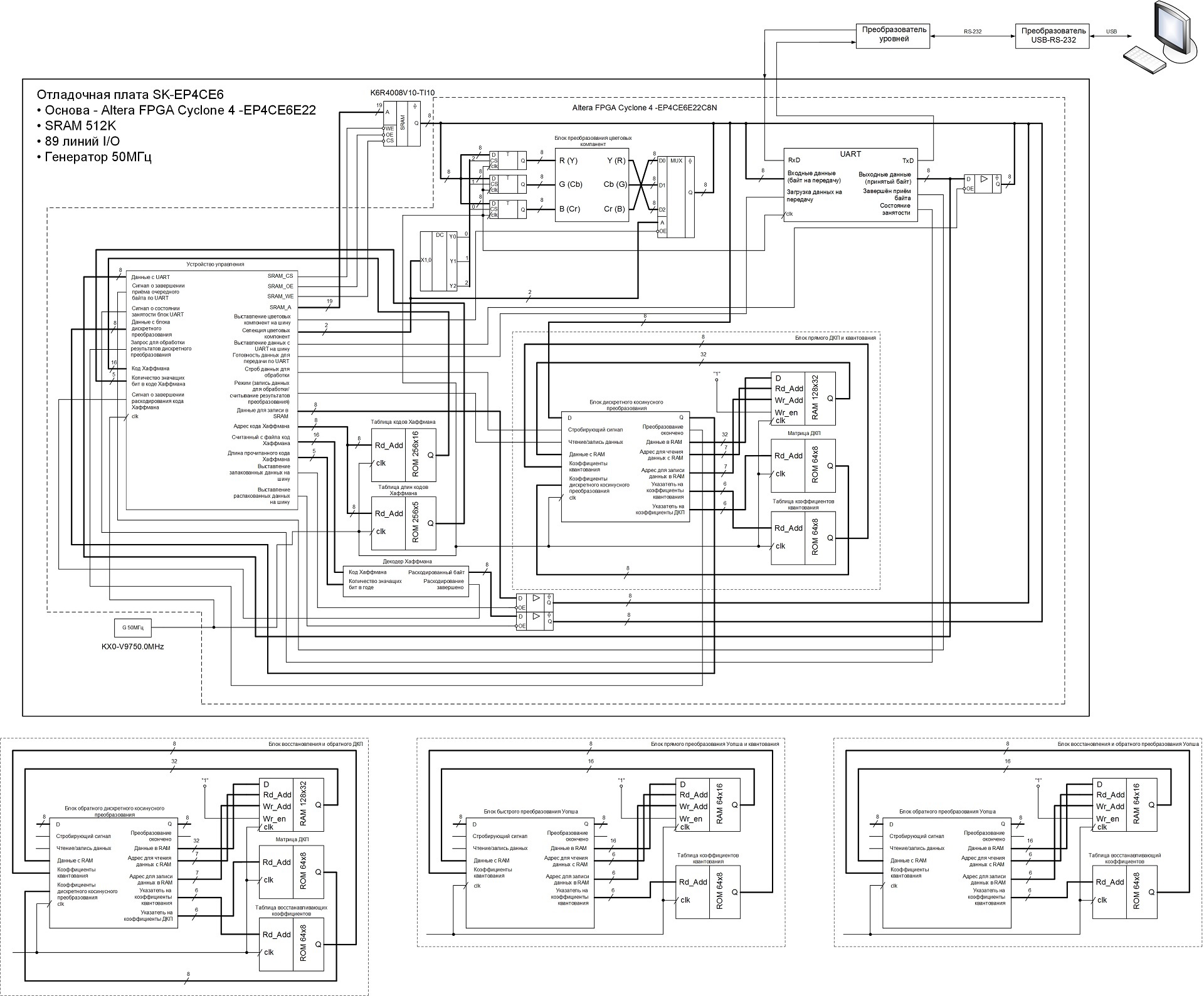
Процесс работы кодека контролирует устройство управления, которое представляет собой конечный автомат, здесь же осуществляется кодирование/декодирование длин серий, а также формирование конечных данных из кодов Хаффмана при сжатии и формирование самих кодов Хаффмана из поступающих с памяти SRAM данных при распаковке. Также устройство управления генерирует управляющие сигналы для других операционных блоков.
Под основной схемой, представлены схемы операционных блоков, меняя которые в основной схеме, я менял режимы работы устройства. Была попытка собрать всё в единое устройство и задавать режимы работы кодека, а также способы базисного преобразования при помощи команд по UART, но не хватило логической ёмкости ПЛИС. Поэтому режимы работы устройства меняются сменой соответствующих операционных блоков и задачей определённых параметров в устройстве управления (в т.ч. и размеры сжимаемого/распаковываемого изображения), после чего изменённый проект компилируется и прошивается в ПЛИС.
В интернете можно найти много различной информации, посвящённой преобразованию цветовых пространств, поэтому сразу начну с описания аппаратной реализации.
Блок преобразования цветовых пространств представляет собой комбинационную логику, благодаря чему преобразование цветовых компонент осуществляется за один такт генератора. Преобразование цветового пространства RGB в YCbCr осуществляется по следующим формулам:

Вычисление начинается с того, что устройство управления выставляет в адресный порт микросхемы памяти SRAM начальный адрес, с которого в .bmp файле хранятся пиксельные данные, как было сказано выше, значение начального адреса — 36h. В файлах .bmp по этому адресу хранится значение синей цветовой компоненты самого нижнего правого пикселя изображения. По адресу 37h — значение зелёной цветовой компоненты, далее красной, потом снова идёт синяя компонента следующего пикселя в самой нижней строке изображения и т. д. Как видно из функциональной схемы, под каждую цветовую компоненту в схеме предусмотрен свой регистр. После загрузки с памяти всех трёх цветовых компонент в свои регистры, со следующего такта генератора осуществляется запись в память результатов вычислений. Так, по адресу синей компоненты «B» записывается монохроматическая красная компонента «Cr», по адресу зелёной компоненты «G» записывается монохроматическая синяя компонента «Cb», и по адресу компоненты «R» записывается компонента яркости «Y». В результате выполнения данного этапа на месте исходного изображения в памяти SRAM, представленного в формате RGB, появится то же изображение в формате YCbCr.
Для аппаратной реализации вычислений яркостной и монохроматических компонент, все дробные коэффициенты из формул были представлены в виде шестнадцатиразрядных слов в формате с фиксированной точкой, где в старших восьми битах содержится целая часть, соответственно в младших восьми — дробная. Например, коэффициент 0.257 в двоичном представлении с фиксированной точкой выглядит так: 0000000001000001 или в шестнадцатиричной форме 0041h. Ограниченность количества разрядов уменьшает точность, так, если дробное двоичное число 0000000001000001 перевести в десятичную форму, то получим: 2^(-2) + 2^(-8) = 0.25 + 0.00390625 = 0.25390625. Как видно, результат отличается от значения 0.257 и для повышения точности представления нужно увеличивать количество разрядов, отводимых под дробную часть. Но я решил ограничиться, как было сказано выше, восемью разрядами.
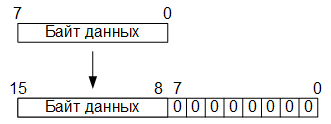
Итак, на первом этапе преобразования, восьмиразрядные значения цветовых компонент RGB преобразуются в шестнадцатиразрядные в формате с фиксированной точкой путём добавления восьми младших разрядов, заполненных нулевыми битами:
На втором этапе осуществляются операции умножения, сложения и/или вычитания. В результате которых получаются тридцатидвухразрядные данные, где в шестнадцати старших разрядах содержится целая часть, в шестнадцати младших — дробная.
На третьем этапе из полученных тридцатидвухразрядных слов формируются восьмиразрядные данные путём выделения восьми разрядов, стоящих непосредственно перед запятой (если порядковый номер самого младшего бита — 0, а самого старшего — 31, то это биты с 23 по 16):
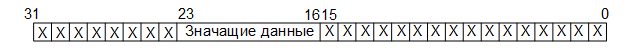
На четвёртом этапе, к полученным восьмиразрядным словам, в соответствии с вышепредставленными формулами, прибавляются смещения (для компоненты Y — 16, для компонент Cb, Cr — 128).
Преобразование из YCbCr в RGB осуществляется по таким формулам:
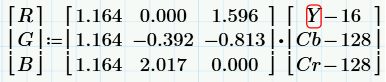
Здесь есть такая особенность, что результаты вычислений, в некоторых случаях, могут приобретать значения большие 255, что выходит за пределы одного байта, либо отрицательные значения, соответственно такие ситуации нужно отслеживать.
Так, если возникает переполнение, то значение итоговой цветовой компоненты должно быть равным 255, для этого просто проводим побитовую логическую операцию «ИЛИ» результата с битом переполнения. А если знаковый разряд результата равен единице (т.е. значение меньше нуля), то значение итоговой цветовой компоненты должно быть равным 0, для этого проводим побитовую логическую операцию «И» результата с инвертированным значением знакового бита.
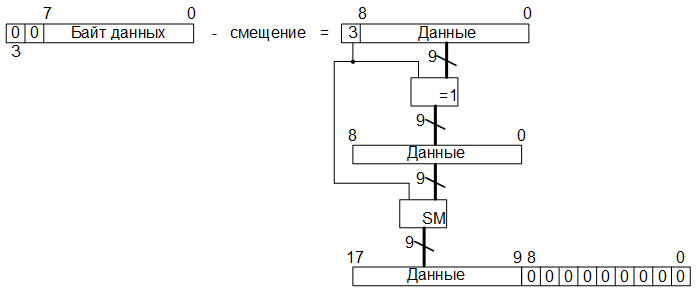
Итак, на первом этапе операции преобразования цветового пространства YCbCr в RGB, считанные с микросхемы памяти SRAM, восьмиразрядные значения яркостной и монохроматических компонент переводим в дополнительный десятиразрядный код, путём добавления двух старших нулевых бит (знаковый бит и признак переполнения). В итоге получаем десятиразрядные слова. Далее в соответствии с формулами отнимаем от данных значений смещения (или прибавляем отрицательные значения смещений, представленные в десятиразрядном дополнительном коде). Затем, полученный результат переводим из дополнительного кода в прямой, сохраняя значения самого старшего (знакового) бита. Оставшиеся девятиразрядные слова преобразуем в восемнадцатиразрядные с фиксированной точкой путём, приписывания младших девяти разрядов с нулевыми битами:
Дробные коэффициенты, фигурирующие в формулах, также представляем в виде восемнадцатиразрядного кода с фиксированной точкой, где под целую и дробную части отводятся по 9 бит. В результате операций умножения получаем тридцатишестиразрядные значения произведений, в которых 18 старших разрядов – целая часть, 18 младших – дробная. Затем вычисляем знак произведения путём проведения логической операции «сложение по модулю 2», ранее сохранённого знакового разряда со знаком, стоящим перед коэффициентом в формуле (если «-», то «1», если «+», то «0»).
Также нужно определить, не является ли результат произведения нулевым, если результат умножения равен нулю, то и в знаковом разряде должен быть записан 0 вне зависимости от знаков, стоящих перед коэффициентами и знаков, стоящих перед результатами, полученных в результате смещения считанных с памяти компонент. Для этого, к произведению применяем оператор редукции (|product[35:0]), который определяет, все ли биты в результате умножения равны нулю (если да, то результат работы данного оператора будет нулевым), после чего проводим операцию логического «И» полученного результата с результатом операции «сложение по модулю 2» знаковых разрядов.
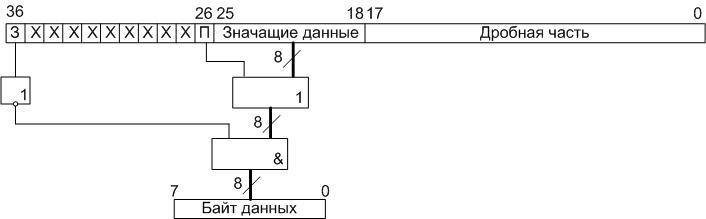
После всего этого переводим результаты умножения в дополнительный тридцатисемиразрядный код, где в самом старшем разряде хранится знак, и проводим операции сложения. После операций сложения, полученные, в дополнительном коде, результаты переводим в прямой код, и выделяем восемь бит, стоящих непосредственно перед запятой (если номер самого младшего бита 0 а самого старшего – 36, то это биты с 25 по 18). Далее проверяем, не было ли переполнения, для этого, как было сказано выше, проводим операцию побитового логического «ИЛИ» выделенных восьми бит с признаком переполнения, который хранится в 26-ом разряде. И ещё, проверяем не получился ли отрицательный результат, для чего проводим побитовую операцию логического «И» инвертированного знакового разряда с этими же восемью битами:
Полученные, в результате вычисления по трём формулам, и преобразованные восьмиразрядные значения и есть значения цветовых компонент RGB.
Тестировать работу устройства я решил при помощи фотографии Лены Содерберг размером 256 на 256 пикселей:

С этой фотографией работают все, кто занимается обработкой изображений, и я решил не быть исключением.
Итак, в результате преобразования исходной фотографии, загруженной по UART в память SRAM отладочной платы, из цветового пространства RGB в пространство YCbCr, было получено следующее изображение:

Ниже на рисунке справа представлена исходная фотография, слева фотография – результат обратного преобразования из пространства YCbCr в цветовое пространство RGB так, как это описывалось выше:

При сравнении исходной и преобразованной фотографии можно увидеть, что исходная фотография ярче обработанной, это объясняется потерей данных, которые возникали при округлении («отбросе» дробной части), а также потерей точности, при представлении дробных коэффициентов в двоичной форме.
Информации о том, что такое дискретное косинусное преобразование (далее по тексту ДКП), на просторах интернета присутствует в предостаточном количестве, поэтому на теории остановлюсь кратко.
Как было сказано в этой публикации, суть любого базового преобразования сводится к умножению матрицы преобразования на матрицу исходных данных, после чего полученный результат снова умножается уже на транспонированную матрицу того же преобразования. В случае с дискретным косинусным преобразованием, коэффициенты матрицы преобразования вычисляются по следующему правилу:
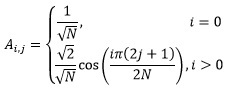
Где:
N — размерность матрицы;
i, j — индексы элементов матрицы.
В нашем случае N = 8, т.е. исходное изображение разбивается на блоки 8 на 8 пикселей, при этом значения индексов i и j изменяются в диапазоне от 0 до 7.
В результате применения этого правила при N = 8 получаем такую матрицу преобразования:
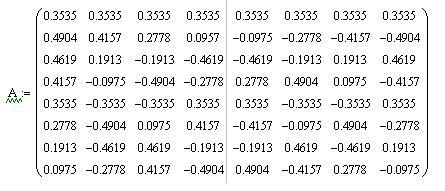
Для того, чтобы не проводить вычисления с дробными числами помножим каждый элемент матрицы на 8v8, и округлим полученные значения элементов матрицы до целых чисел, в результате чего получим матрицу Т:
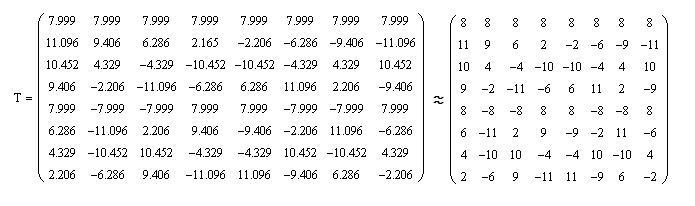
При этом, необходимо будет результат умножения матриц, как в случае прямого дискретного косинусного преобразования при кодировании, так и в случае обратного при декодировании, разделить на 512. Учитывая, что 512 = 2^(9), то деление осуществляется методом сдвига делимого вправо на 9 позиций.
В результате прямого дискретного косинусного преобразования получается матрица, так называемых, коэффициентов ДКП, в которой элемент, расположенный в нулевой строке и нулевом столбце, называется низкочастотным коэффициентом и его значение всегда положительное. Остальные элементы матрицы ДКП – высокочастотные коэффициенты, значения которых могут быть как положительными, так и отрицательными. Учитывая это, и то, что элементы результирующей матрицы должны быть восьмиразрядными, для низкочастотного коэффициента диапазон значений составит [0..255], а для высокочастотных – [-127..127]. Для того, чтобы уложиться в эти диапазоны необходимо результаты прямого дискретного косинусного преобразования разделить на 8, соответственно результаты обратного – помножить на 8. В результате для прямого ДКП получаем такую формулу:
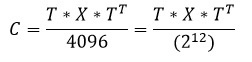
Где:
С – матрица коэффициентов дискретного косинусного преобразования;
Т – матрица преобразования;
Х – матрица 8 на 8 яркостной или монохроматических компонент (в зависимости от того какая, назовём так, компонентная плоскость Y, Cb или Cr кодируется).
Для обратного ДКП получаем следующую формулу:
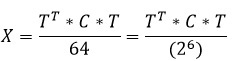
Коэффициенты матрицы T в восьмиразрядном формате хранятся в памяти ROM, расположенной на кристалле ПЛИС в прямом коде, при этом старший бит содержит знак.
И так, на первом этапе дискретного косинусного преобразования, с памяти SRAM в операционный блок, осуществляющий прямое ДКП, последовательно считываются 64 байта одной из компонент (сначала кодируется вся компонентная плоскость Y, затем Cb и Cr), образующие часть изображения, как было написано ранее, размером 8 на 8 пикселей (при этом адреса для памяти SRAM генерируются особым образом):
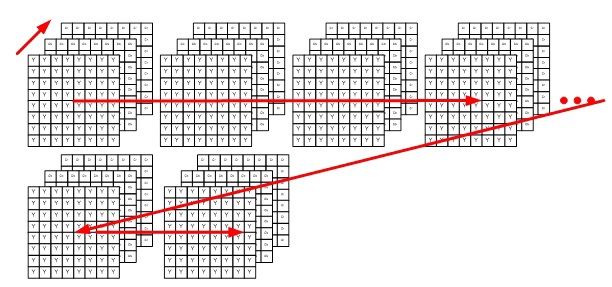
Операции вычисления в данном блоке осуществляются с двадцатиодноразрядными данными: 12 младших разрядов – значения, которые будут потерянны при делении на 4096 (2^(12)), 8 разрядов – значащая часть и старший разряд – знак, итого: 12+8+1 = 21:
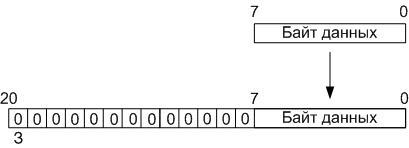
Исходя из этого, во время загрузки, восьмиразрядные данные в операционном блоке преобразуются в двадцатиодноразрядные слова, представленные в дополнительном коде, путём приписывания старших тринадцати разрядов, заполненных нулевыми битами (старший бит — знак), после чего полученное слово запоминается в буферную память RAM, расположенную, также, на кристалле ПЛИС, в адресное пространство c 00h по 3Fh (среда Quartus II не позволила создать память RAM с организацией 128х21, поэтому пришлось использовать память с организацией 128х32).
На втором этапе, после того как в буферную память RAM записано 64 двадцатиодноразрядных слова (блок 8 на 8), запускается процесс умножения матриц. При этом, с памяти ROM считывается восьмиразрядный строковый элемент матрицы преобразования, который «разворачивается» в двадцатиодноразрядное слово, путём записывания седьмого (знакового) бита значения, считанного с памяти ROM, в двадцатый (знаковый) бит распакованного слова. Остальные семь бит, считанного восьмиразрядного значения элемента матрицы преобразования, переписываются в семь младших бит распакованного слова, биты с порядковыми номерами 7 – 19 заполняются нулями:
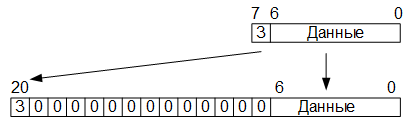
Далее, с буферной памяти RAM считывается, ранее записанный туда, двадцатиодноразрядный столбцовый элемент, после чего, его двадцать младших разрядов перемножаются с двадцатью разрядами развёрнутого элемента матрицы преобразования. Знак произведения вычисляется также, как и при преобразовании цветовых пространств:
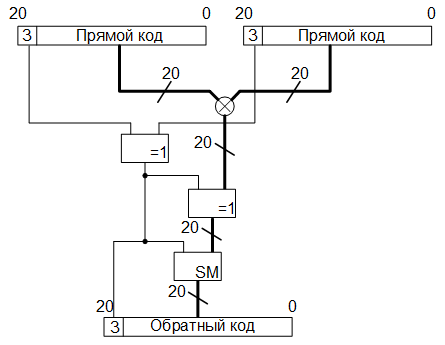
Произведение переводится в дополнительный код и запоминается в стек, глубиной 8 двадцатиодноразрядных слов. Как только стек заполнен (это означает, что элементы строки матрицы преобразования перемножены на элементы очередного столбца исходной матрицы), все значения стека суммируются и результат в дополнительном коде, записывается в буферную память RAM, в адресное пространство с 40h по 7Fh.На третьем этапе, с буферной памяти RAM, с адресного пространства 40h – 7Fh, построчно считываются элементы матрицы, которая является результатом произведения матриц преобразования и исходной матрицы, и преобразуются в прямой код. А с памяти ROM, также как и ранее, считываются, также построчно, и разворачиваются элементы матрицы преобразования (вопреки правилу умножения матриц, здесь мы перемножаем строку на строку, что означает операцию транспонирования матрицы множителя). Затем, также как и раньше, в прямом коде перемножаются двадцатиразрядные элементы матриц, вычисляется знаковый разряд, произведение переводится в дополнительный код и запоминается в стек. Как только стек заполняется восемью элементами, осуществляется их суммирование, и результат из дополнительного кода переводится в прямой.
Далее осуществляется операция квантования. Каждый элемент полученной матрицы делится на, так называемый, соответствующий коэффициент квантования, таблица которых хранится в отдельной памяти ROM на кристалле ПЛИС. Значения коэффициентов квантования рассчитывались по следующей формуле:
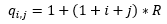
Где:
R – коэффициент сжатия, или коэффициент характеризующей потери качества восстановленным изображением по отношению к исходному;
i, j – индексы вычисляемого элемента матрицы квантования, изменяются в пределах от 0 до 7.
Тут же нужно сказать, что для всех компонентных плоскостей Y, Cb, Cr в кодеке используется одна матрица квантования, вычисленная для R = 2 (не стал я заморачиваться, делая для каждой плоскости свою таблицу коэффициентов квантования).
Для того, чтобы аппаратно не реализовывать делитель, операцию деления при квантовании я заменил операцией умножения следующим образом:
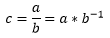
Где:
a – квантуемый коэффициент, элемент результативной матрицы базового преобразования;
b – соответствующий коэффициент матрицы квантования, вычисленный по ранее приведённой формуле;
c – результат квантования.
Соответственно, в память ROM записаны результаты возведения в степень -1 (или 1/b), представленные в формате с фиксированной точкой, при этом в памяти хранятся только 8 разрядов дробной части, так как целая часть всегда равна 0.
Процесс квантования в кодеке реализован следующим образом: как только вычислен и переведён из дополнительного кода в прямой, очередной двадцатиодноразрядный элемент результирующей матрицы линейного преобразования, определяется, является ли этот элемент низкочастотным коэффициентом и если да, разряды с 19 по 12 записываются в восемь старших разрядов промежуточного шестнадцатиразрядного регистра, 8 младших разрядов данного регистра, при этом, заполняются нулями (разряды с 11 по 0 исходного двадцатиодноразрядного слова отбрасываются, так осуществляется операция деления на 4096).
Если элемент является высокочастотным коэффициентом, то в самый старший разряд промежуточного регистра записывается 0, в семь следующих разрядов переписываются разряды с 18 по 12 двадцатиодноразрядного слова, а 8 младших разрядов промежуточного регистра, также, заполняются нулями. Выходы с данного промежуточного регистра подключены к одному из входных портов умножителя 16х16, на другой порт данного умножителя подаются значения из памяти ROM, где хранятся дробные части коэффициентов квантования, возведённых в степень -1. Причём, на 8 старших выводов порта подаются нулевые значения, а на 8 младших – значения считанные с памяти ROM.
Далее, с тридцатидвухразрядного выходного порта умножителя считывается результат квантования, в котом 16 младших разрядов – дробная часть, которая отбрасывается, а 8 разрядов, стоящих непосредственно перед фиксированной запятой, это значащая часть (я думаю и так понятно, что результат квантования – это дробное число, представленное в формате с фиксированной точкой). Причём, в случае с низкочастотными коэффициентами, значащей частью являются не 8, а 7 разрядов, стоящих непосредственно перед запятой, в восьмой разряд здесь переписывается знак, полученный ещё на этапе базового преобразования, находящийся в самом старшем разряде:
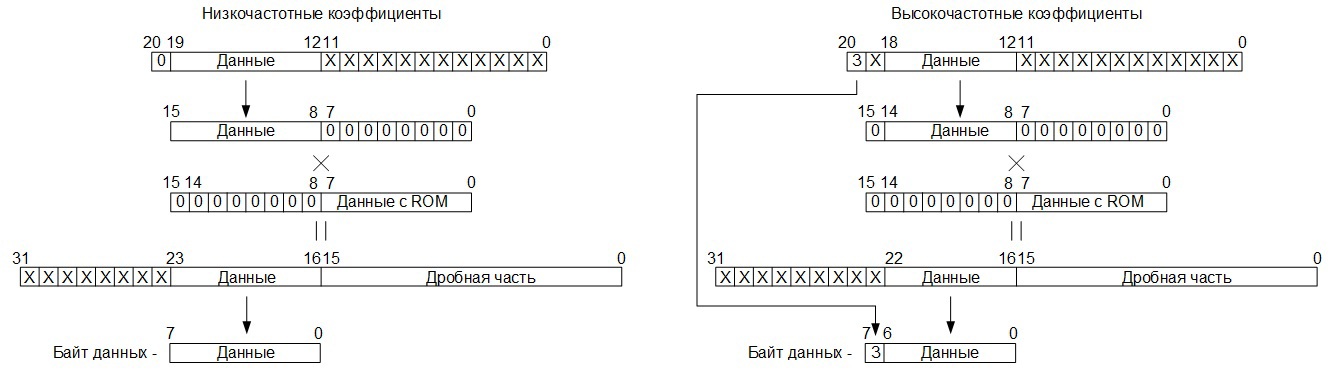
Ну и далее, сформированные восьмиразрядные значения записываются в буферную память RAM в адресное пространство 00h – 3Fh:
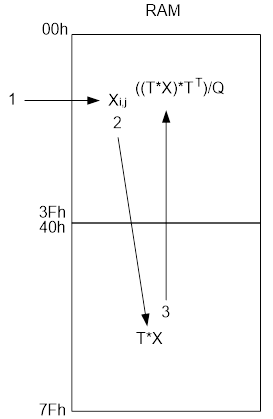
Готовые данные с буферной памяти считываются в соответствии с алгоритмом зигзаг-сканирования (что такое зигзаг-сканирование можно прочитать здесь) и идут на этап кодирования длин серий.
Декодирование идёт в обратном порядке. И здесь мы оперируем уже пятнадцатиразрядными данными: 6 младших разрядов – разряды, которые теряются при делении на 64, 8 разрядов – значащая часть, 1 разряд – знак. Итого: 6+8+1 = 15:
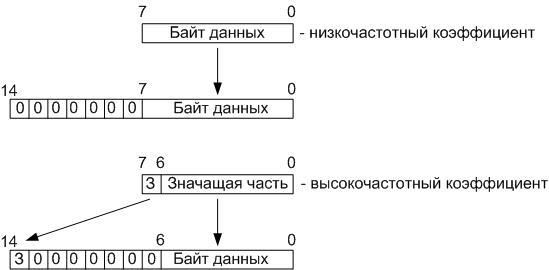
На первом этапе, поступившее в операционный блок, осуществляющий обратное дискретное косинусное преобразование, восьмиразрядное слово разворачивается до пятнадцатиразрядного. Для это, сначала осуществляется проверка, не является ли поступивший байт низкочастотным коэффициентом, и если да, то все 8 разрядов переписываются в 8 младших разрядов пятнадцатиразрядного слова. А если поступил высокочастотный коэффициент, то 7 младших разрядов поступившего байта переписываются в 7 младших разрядов пятнадцатиразрядного слова, а старший разряд, содержащий знак, записывается в самый старший разряд пятнадцатиразрядного слова.
Затем развёрнутые до 15-ти разрядов данные записываются в буферную память RAM в адресное пространство 00h – 3Fh в соответствии с алгоритмом зигзаг-сканирования. После того как в памяти RAM будет сформирована матрица квантованных коэффициентов ДКП размером 8 на 8, начинается процесс обратного дискретного косинусного преобразования, также как было описано выше. При этом каждое считанное пятнадцатиразрядное слово с RAM, сначала проходит процедуру восстановления (процедура обратная квантованию) путём умножения на соответствующий коэффициент квантования, хранящийся в памяти ROM.
Здесь осуществляется умножение четырнадцатиразрядного слова на восьмиразрядный коэффициент квантования, который является целым числом (это те значения, которые при сжатии возводились в степень -1). Далее осуществляется перемножение матриц также, как было описано выше. После чего из получившихся пятнадцатиразрядных значений отбрасываются 6 младших разрядов (деление на 64) и проверяется знаковый разряд, и если его значение равно 0, то 8 последующих разрядов содержат результирующее значение декодируемой компоненты Y, Cb или Cr (в зависимости от того, какая компонентная плоскость декодируется). А если знаковый разряд равен 1, то следующие 8 разрядов просто обнуляются (т.е. округляются до 0, т.к. результат обратного ДКП не может быть отрицательным).
Получаемые восьмиразрядные результаты обратного ДКП записываются в буферную память RAM, формируя, таким образом, блок изображения 8 на 8. После того как блок сформирован, каждый его элемент переписывается во внешнюю память SRAM по соответствующему адресу, формируя там, в свою очередь, конечное изображение в пространстве YCbCr.
И вот, наконец-то мы дошли до того, ради чего всё затевалось. Преобразование Уолша – разновидность базового преобразования, матрица преобразования которого выглядит следующим образом:
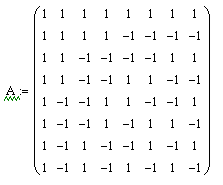
Информацию о том, откуда эта матрица берётся, как выводится и как формируется, можно, также, найти в интернете или в учебниках по теории цепей и сигналов. Останавливаться здесь на этом не будем.
Итак, как было сказано выше, базовое преобразование сводится к умножению матрицы преобразования на матрицу исходных данных, после чего полученный результат снова умножается уже на транспонированную матрицу того же преобразования. Значения всех элементов матрицы преобразования Уолша равны либо 1, либо -1, соответственно аппаратно потребуется выполнять только операции сложения данных, представленных в дополнительном коде. Если расписать процесс умножения матрицы Уолша на исходную матрицу блока изображения 8 на 8, то получим следующие выражения для каждого строкового элемента промежуточной матрицы:
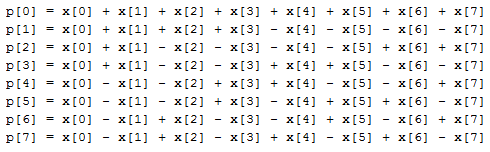
Где:
p[0..7] — очередная строка промежуточной матрицы;
x[0..7] — очередная строка исходной матрицы, являющейся блоком изображения 8 на 8.
И далее, если расписать процесс умножения промежуточной матрицы на транспонированную матрицу Уолша, то получим такие выражения для каждого уже столбцового элемента результирующей матрицы:

Где:
y[0..7] — очередной столбец результирующей матрицы;
p[0..7] — очередной столбец промежуточной матрицы.
Также как и в случае с ДКП, верхний левый элемент результирующей матрицы, будет являться низкочастотным коэффициентом, значение которого всегда больше 0, а остальные 63 элемента — высокочастотные коэффициенты, значения которых могут быть как меньше так и больше 0 (также как и при ДКП).
Аппаратно, блок преобразования Уолша, представляет собой группу сумматоров подключённых определённым образом, на входы которых сначала поочерёдно подаются строки исходной матрицы, результаты при этом запоминаются в буфер, а затем из буфера на входы этой же группы сумматоров поочерёдно подаются столбцы, ранее полученной матрицы. Также нужно учесть, что при прямом преобразовании Уолша, значения элементов результирующей матрицы могут выходить за пределы 255, поэтому их нужно будет разделить на 64 или сдвинуть на 6 разрядов вправо.
Обратное преобразование Уолша осуществляется точно также с тем лишь исключением, что элементы результирующей матрицы, которая будет являться блоком изображения 8 на 8 не нужно не на что делить, значения уже получаются нормированными.
Итак, в блоке прямого преобразования Уолша поступающие восьмиразрядные значения компонент, по аналогии с блоком ДКП, разворачиваются в пятнадцатиразрядные (6 разрядов — разряды которые будут потеряны при делении на 64, 8 разрядов — значащие разряды, 1 разряд — знак) и записываются в буферную память RAM. Как только в буфере сформирована матрица 8 на 8, из буфера построчно считываются элементы исходной матрицы, преобразуются, и записываются в адреса той же строки, откуда были считаны. Это позволяет использовать память RAM c организацией 64х15 (в случае с ДКП потребовался буфер с организацией 128х21), но Quartus II позволил создать блок памяти RAM только с организацией 64х16, один разряд остался не использованным (хотя в случае с ДКП не использовалось 11 разрядов).
Затем из буфера считываются уже столбцы матрицы, полученной на предыдущем этапе, преобразуются, и результат этого преобразования переводится из дополнительного кода в прямой, после чего абсолютно также, как и в случае прямого ДКП осуществляется операция квантования, результат которой записывается в буферную память RAM откуда, затем считывается в соответствии с алгоритмом зигзаг-сканирования. Обратное преобразование Уолша осуществляется аналогично прямому, поступающие данные при этом записываются в буферную память RAM в по алгоритму зигзаг-сканирования, а при считывании для непосредственного преобразования Уолша, домножаются на соответствующие коэффициенты квантования.
Ниже, в сравнительной форме, представлены результаты работы блоков прямого преобразования Уолша и прямого дискретного косинусного преобразования:

Сверху слева представлена фотография, на которой мы тренируемся, которая сначала была переведена, скажем так, внутри нашей отладочной платы, из цветового пространства RGB в пространство YCbCr, затем каждая компонентная плоскость была разбита на блоки 8 на 8 и преобразована по правилу прямого преобразования Уолша. Сверху справа та же фотография, преобразованная по правилу прямого ДКП. Снизу слева результат преобразования Уолша, подвергнутый операции квантования, соответственно, снизу справа, подвергнутый операции квантования, результат прямого ДКП, считанные с отладочной платы.
Алгоритм кодирования длин серий ещё, по-другому, называют алгоритмом сжатия, использующим исключение повторов (RLE – Run Length Encoding). В основе данного алгоритма лежит принцип определения групп одинаковых, идущих подряд символов (байт с одинаковыми значениями), и заменой их определённой структурой, содержащей количество повторов и код повторяющихся символов, т.е. <количество повторов><повторяющийся символ (байт)>. Очевидно, что максимальное количество одинаковых символов (байт данных), которые можно закодировать такой структурой, зависит от длины кода количества повторов.
Для реализации, решено было выбрать алгоритм, который реализован в графическом формате .pcx. В этом алгоритме RLE особенность в том, что количество повторов кодируется байтом-счётчиком, в котором старшие два бита содержат единицы, а младшие шесть содержат количество повторов. Соответственно значения байт, которые подряд не повторяются и значения которых меньше С0h переписываются в поток сжатых данных без изменения. А не повторяющиеся подряд значения байт большие C0h, (две единицы в старших разрядах), при записи в выходной поток, в любом случае, предваряются байтом счётчиком, и, так как такой символ в потоке один, то и байт счётчик принимает значение С1h. Также нужно учитывать, что максимальное число повторов, которое можно закодировать в шести выделяемых битах, составляет 63=3Fh, поэтому, после каждого увлечения счётчика повторов, нужно проверять, не составило ли его значение 63, и если да, в выходной поток, сначала, нужно выставить значение FFh (C0h(префикс байта-счётчика)+3Fh(количество повторов) = FFh), а затем значение повторяющегося байта, после чего счётчик обнуляется и подсчёт начинается снова.
Например, на выходе блока базового преобразования (будь то блок прямого ДКП или быстрого преобразования Уолша) имеем следующий поток данных, выдаваемых с буферной памяти RAM в соответствии с алгоритмом зигзаг-сканирования: ECh, C2h, 03h, 0Ah, 0Ah, D1h, D1h, 01h, 01h, 01h, 00h, 00h, 00h, 00h, 00h, 02h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h. Тогда, после кодирования данного потока, алгоритмом RLE, получим следующий поток данных: C1h, ECh, C1h, C2h, 03h, C2h, 0Ah, C2h, D1h, C3h, 01h, C5h, 00h, 02h, F0h, 00h.
Итого, в нашем случае, из строки длинной 64 байта, после сжатия получена строка длинной 16 байт, в которой наибольшее количество повторов принадлежит нулевым байтам. Эти нулевые байты и есть, округленные до нуля после квантования, высокочастотные коэффициенты, соответственно, если квантование не проводить, то количество подряд идущий нулевых байт будет значительно ниже, что даст более низкую степень сжатия, но позволит сохранить качество изображения.
Аппаратно, данный алгоритм реализуется довольно-таки просто как при сжатии так и при распаковке.
При распаковке после получения очередного байта, проверяем его старшие два бита, и если их значения равны единице, то младшие шесть байт загружаем в счётчик, считываем последующий бай, не проверяя его старших бит, выставляем его в выходной поток, декрементируя, при этом, счётчик до тех пор, пока он не обнулится, после чего читаем следующий байт с потока, а если же значения старших бит счётчика отличны от двух единиц, то переписываем этот байт в выходной поток без изменений.
В кодеке, кодирующий алгоритм RLE выполняется устройством управления во время считывания байт данных с блока базового преобразования при сжатии, декодирующий алгоритм RLE, выполняется перед загрузкой данных в блок базового преобразования при распаковке (я думаю, это и так понятно).
Алгоритму Хаффмана была посвящена не одна статья, опубликованная на этом сайте, поэтому, также как и ранее, на теории останавливаться не буду. Скажу лишь то, что по аналогии с алгоритмом JPEG, в описываемом здесь устройстве, я реализовал алгоритм Хаффмана с, заранее вычисленными, фиксированными таблицами.
Отличие от алгоритма JPEG в том, что в JPEG в таблицах хранятся только длины кодов, а не сами коды, в рассматриваемом же устройстве, в одной памяти ROM отдельно хранятся шестнадцатиразрядные коды Хаффмана, а в другой памяти ROM, хранятся количества значащих бит в каждом из шестнадцатиразрядных кодов, начиная с самого старшего. Также в JPEG для низкочастотных и высокочастотных коэффициентов используются разные таблицы, и вместо самих значений низкочастотных коэффициентов, кодируются их разности. В своём же устройстве я всё так усложнять не стал (может быть зря) и, в разработанном мной устройстве, все коэффициенты кодируются единым потоком и единой таблицей.
Кодирование осуществляется так: на адресные входы блоков памяти ROM, подаются кодируемые байты (поток данных, закодированных по алгоритму RLE), при этом, с выхода блока памяти ROM, где хранятся коды Хаффмана, считывается то количество бит, значение которого было считано с выхода другого блока памяти ROM. Коды Хаффмана и их длины хранятся по тем адресам, значения которых соответствует значениям кодируемых байт.
Далее, из считываемого потока бит, формируются байты и записываются в память. Например, при кодировании одного байта, с памяти ROM, содержащей код Хаффмана, было считано 4 бита, при кодировании второго байта в потоке – 11 бит, третьего – 3, и четвёртого – 4. Итого, получаем 4+11+3+4 = 22, 22 бита делим на 8 получаем 2 байта и 6 бит, к которым дописываем, в младшие разряды, два нулевых бита (так кодируется самый последний байт в потоке) и получаем 3 равноценных байта, которые и записываются во внешнюю память, т.е. из четырёх байт на входе получили три на выходе.
Декодер Хаффмана реализован в виде таблицы истинности, на языке AHDL (в данном языке предусмотрен для этого специальный оператор “TABLE”, хотя, можно было это сделать и на языке Verilog при помощи оператора “case”, кому как больше нравится), у которой один шестнадцатиразрядный входной порт, для кода Хаффмана и один пятиразрядный входной порт для длины этого кода.
Декодирование осуществляется так: с внешней памяти SRAM считывается байт, который побитно загружается в шестнадцатиразрядный регистр, начиная со старшего разряда, выходы которого подключены к шестнадцатиразрядному входному порту Декодера Хаффмана (той самой таблицы), после загрузки очередного бита, осуществляется инкрементирование счётчика, подключенного к другому порту декодера Хаффмана.
После загрузки очередного бита, проверяется сигнал, означающий, что входной комбинации кода Хаффмана и длины кода, найден выходной байт, и если значение данного сигнала равно логической единице, то с выходного порта декодера Хаффмана считывается байт, который идёт на декодирование по алгоритму RLE. При этом шестнадцатиразрядный регистр обнуляется, а оставшиеся в байте биты загружаются в него вновь со старшего разряда, если биты в считанном с внешней памяти байта закончились, то считывается новый байт и т.д.
На первом этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе быстрого преобразования Уолша, с квантованием коэффициентов. В итоге, загруженное по UART в устройство, наше тестовое изображение размером 256 на 256 точек с объёмом занимаемой памяти 192 Кбайта, было преобразовано (сжато) в файл с объёмом занимаемой памяти 8,1 Кбайт.
На втором этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе быстрого преобразования Уолша, но без квантования коэффициентов. В итоге, то же изображение было преобразовано (сжато) в файл с объёмом занимаемой памяти 43,8 Кбайт.
На третьем этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе дискретного косинусного преобразования, с квантованием коэффициентов. В итоге, загруженное по UART в устройство, наше тестовое изображение размером 256 на 256 точек с объёмом занимаемой памяти 192 Кбайта, было преобразовано (сжато) в файл с объёмом занимаемой памяти 8,17 Кбайт.
На четвёртом этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе дискретного косинусного преобразования, уже без квантования коэффициентов. В итоге, то же изображение было преобразовано (сжато) в файл с объёмом занимаемой памяти 35,9 Кбайт.
Ниже представлены результаты распаковки, разработанным устройством, ранее сжатых изображений.
На рисунке, представленном ниже, в центре показано исходное изображение, слева – изображение, сжатое с квантованием коэффициентов, при помощи быстрого преобразования Уолша, справа – изображение, сжатое с квантованием коэффициентов, при помощи дискретного косинусного преобразования:

Разницу в базовых преобразованиях отчётливо при увеличении одинаковых участков изображений. Так, преобразование Уолша даёт более контрастные границы на участках переходов, в свою очередь, ДКП делает переходы на границах более плавными.
Ниже представлены результаты распаковки изображений, которые сжимались без квантования коэффициентов. Также как и в предыдущем случае, в центре — исходное изображение, слева – изображение, сжатое при помощи быстрого преобразования Уолша, справа – при помощи ДКП:

На первый взгляд, особых потерь в качестве нет, но если изображения увеличить, то можно увидеть, границы блоков 8 на 8, которые, в случае преобразования Уолша, также имеют более контрастные границы, а случае с ДКП – более плавные. Вообще, касательно вопросов оценки качества изображений написан целый ряд работ, и заниматься здесь этим не очень хочется.
И так, ниже представлена таблица, содержащая результаты определения характеристик сжатия, полученных на разработанном устройстве, изображения, размером 256 на 256 пикселей представленного в формате .bmp с объёмом занимаемой памяти (Lисх.) 192 КБайта. Размер исходного изображения вычисляется так: 256?256 = 65536 точек, на каждую точку приходится по три байта (1 байт – красная компонента, 1 байт – зелёная компонента, 1 байт – синяя компонента), получаем 65536?3 = 196608 байта, плюс ещё 53 байта – заголовок, итого получаем 196661 байт или 196661/1024 ? 192 КБайта с «копейками»:
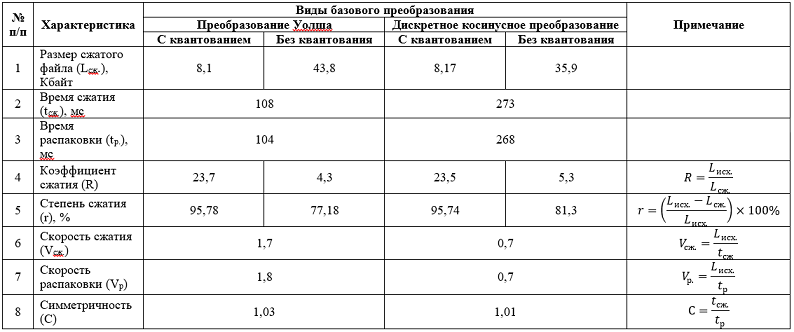
Из таблицы видно, что оба способа базового преобразования в аппаратной реализации, дают, практически, одинаковые результаты, за исключением времени и скорости сжатия/распаковки. Здесь преобразование Уолша выигрывает у частного случая преобразования Фурье — ДКП. 1 — 0 в пользу преобразования Уолша.
Если сравнивать оба вида преобразования с точки зрения затрат аппаратных ресурсов ПЛИС, то получим следующее:
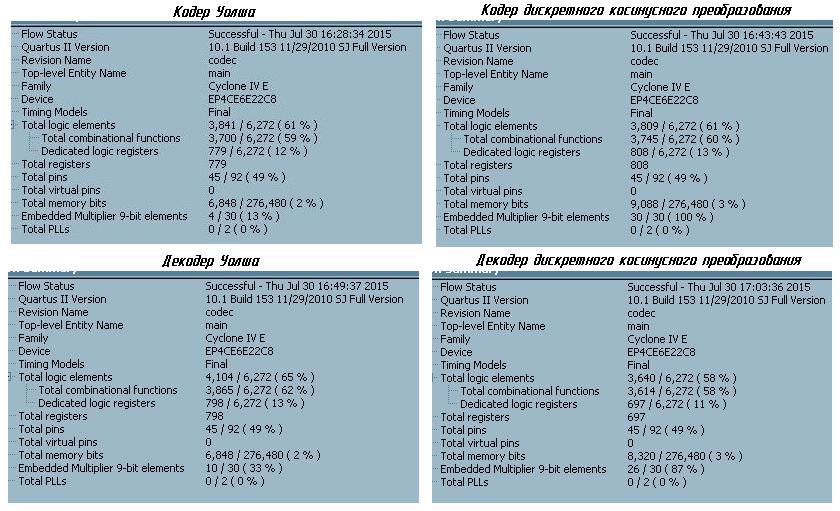
Из представленных скриншотов видно, что аппаратных ресурсов ПЛИС, оба преобразования потребляют одинаково, за исключением использования встроенных умножителей. Здесь частный случай преобразования Фурье снова проиграл преобразованию Уолша. Итого: 2 — 0 в пользу преобразования Уолша.
В принципе, можно сделать такой вывод, что с очки зрения аппаратной реализации лучше использовать, в качестве базового преобразования, преобразование Уолша.
Ну и в самом заключении хочется отметить, что данный аппаратный кодек сжатия/распаковки изображений, разрабатывался, скажем так, необдуманно и непродуманно. Именно этим и объясняется неудовлетворительные (по крайней мере, мне так показалось) значения временных характеристик сжатия/распаковки. Просматривая проект снова и снова, я всё время нахожу возможности оптимизации и варианты уменьшения времени обработки изображения, с одновременным увеличением размера, обрабатываемого (сжимаемого/распаковываемого) изображения. В итоге, можно будет добиться скорости сжатия/распаковки — 24 изображения в секунду, что позволит обрабатывать видео потоки.
Ну вот, на этом всё. Спасибо за внимание!
Для начала хочу поблагодарить автора статей «Декодирование JPEG для чайников» и «Изобретаем JPEG», которые очень помогли мне в работе по написанию данной публикации. Когда я занялся вопросами изучения алгоритмов сжатия изображений с потерями, то в части алгоритма JPEG меня всё время мучил вопрос: «Почему роль базисного преобразования в алгоритме JPEG отведена именно частному случаю преобразования Фурье?». Здесь автор даёт ответ на этот вопрос, но я решил подойти к нему не с точки зрения теории, математических моделей или программной реализации, а с точки зрения схемотехники.
Алгоритм сжатия изображений JPEG является алгоритмом цифровой обработки сигналов, которые, аппаратно, как правило, реализуются либо на цифровых сигнальных процессорах, либо на программируемых логических интегральных схемах. В моём случае, выбор для работы цифрового сигнального процессора означал бы приход к тому, от чего я пытался уйти — к программной реализации, поэтому решено было остановиться на программируемой логике.
В одном из интернет-магазинов я приобрёл довольно простую отладочную плату, которая содержит в своём составе ПЛИС Altera FPGA Cyclone 4 -EP4CE6E22 и память SRAM 512Kx8. Так как ПЛИС была фирмы Altera, то и для разработки решено было использовать среду Quartus II Web Edition. Разработка отдельных функциональных блоков аппаратного кодека осуществлялась на языке Verilog, а сборка в единую схему производилась в графическом редакторе среды Quartus II Web Edition.
Для связи с персональным компьютером (приём команд, приём/передача обрабатываемых данных), на языке Verilog мной был написан простенький асинхронный приёмопередатчик UART. Для подключения к COM-порту (RS-232) компьютера, на базе микросхемы MAX3232WE и из того, что было под рукой, наспех, был спаян преобразователь уровней. В итоге вот, что получилось:

Для отправки команд с персонального компьютера, а также приёма-передачи данных использовалась триальная версия программы ADVANCED SERIAL PORT MONITOR, которая позволяет формировать не только отдельные посылки байт данных, но и формировать потоки данных из содержимого файлов, а также записывать принимаемые потоки данных в файл, что позволило передавать и принимать файлы. Никакие протоколы и контрольные суммы, для для приёма/передачи данных по UART я тут не использую и не контролирую (попросту лень было всё это предусматривать и реализовывать), во время связи для приёма/передачи я использовал, что называется, «сырые данные».
Все арифметические операции связанные с дробными числами в кодеке осуществляются в формате с фиксированной точкой, операции сложения и вычитания осуществляются в дополнительном коде, в принципе это и так понятно. Как определялась разрядность обрабатываемых данных будет описано ниже.
Операция сжатия осуществляется над исходными изображениями, представленными в формате .bmp с глубиной цвета — 24 бита на пиксель (по 8 бит на каждую из цветовых компонент).
Имеющаяся на отладочной плате память была организована следующим образом: адреса с 00000h по 3FFFFh (в шестнадцатиричной системе счисления) выделены под хранение исходных данных (рисунок в формате .bmp для сжатия, либо закодированные данные для распаковки), итого 256 КБ, остальные 256 КБ — пространство для записи получаемых, в результате сжатия или распаковки данных, это адреса с 40000h по 7FFFFh. Я думаю, очевидно, что максимальный размер сжимаемых изображений ограничен объёмом, выделяемой для хранения данных, памяти.
Алгоритм работы устройства такой: сразу после подачи питания кодек ожидает поток данных по UART, любые принятые, при этом, данные здесь интерпретируются как исходный файл для обработки, если пауза между байтами составляет 10 мс, то это интерпретируется как конец файла, и следующий за паузой байт, принимаемый по UART, воспринимаются устройством как команда. Команды представляют собой конкретные значения байт. Например, после приёма файла через 10 мс, поступившее в кодек по UART, значение байта AAh интерпретируется устройством как команда, по которой происходит выдача по UART на компьютер данных с микросхемы памяти, начиная с адреса 40000h и до значения адреса на котором завершилась запись обработанных данных, т.е. на компьютер передаются результаты сжатия/распаковки. Значение EEh интерпретируется как команда на сжатие/распаковку изображения, также для отладки мной был предусмотрен ряд других команд.
Что касается структуры файла с жатым изображением, то тут я решил не заморачиваться, и, в отличии от алгоритма JPEG, реализуемый мной алгоритм, носит довольно-таки узконаправленный характер и не рассчитан на все случаи жизни, поэтому получаемые, в результате сжатия, данные единым потоком записываются в выделенную область памяти. Единственное, что тут нужно отметить, для того чтобы не реализовывать генератор заголовка .bmp файла (тоже было лень), при сжатии он просто целиком переписывается в начальную (с адреса 40000h) область памяти, отведённую для конечных данных, а затем уже, начиная со смещения, с которого в исходном .bmp файле хранятся пиксельные данные, записываются сжатые данные. Это смещение храниться в заголовке .bmp файла по адресу 0Ah относительно его начала, и, как правило составляет 36h. При распаковке, соответственно осуществляется такая же операция.
Итак, сжатие изображений JPEG-подобными алгоритмами осуществляется в следующей последовательности:
- преобразование цветового пространства из RGB в YCbCr или YUV;
- цветовая субдискретизация;
- базисное преобразование;
- квантование коэффициентов получаемых после базисного преобразования;
- зигзаг-сканирование;
- кодирование длин серий;
- сжатие по алгоритму Хаффмана.
Распаковка идёт в обратном порядке.
Из всех, вышеперечисленных этапов, в кодеке я не реализовывал субдискретизацию, так как посчитал её лишней (может быть я не прав).
Исходя из представленной выше последовательности действий, мной была разработана следующая функциональная схема кодека:

Процесс работы кодека контролирует устройство управления, которое представляет собой конечный автомат, здесь же осуществляется кодирование/декодирование длин серий, а также формирование конечных данных из кодов Хаффмана при сжатии и формирование самих кодов Хаффмана из поступающих с памяти SRAM данных при распаковке. Также устройство управления генерирует управляющие сигналы для других операционных блоков.
Под основной схемой, представлены схемы операционных блоков, меняя которые в основной схеме, я менял режимы работы устройства. Была попытка собрать всё в единое устройство и задавать режимы работы кодека, а также способы базисного преобразования при помощи команд по UART, но не хватило логической ёмкости ПЛИС. Поэтому режимы работы устройства меняются сменой соответствующих операционных блоков и задачей определённых параметров в устройстве управления (в т.ч. и размеры сжимаемого/распаковываемого изображения), после чего изменённый проект компилируется и прошивается в ПЛИС.
Преобразование цветового пространства
В интернете можно найти много различной информации, посвящённой преобразованию цветовых пространств, поэтому сразу начну с описания аппаратной реализации.
Блок преобразования цветовых пространств представляет собой комбинационную логику, благодаря чему преобразование цветовых компонент осуществляется за один такт генератора. Преобразование цветового пространства RGB в YCbCr осуществляется по следующим формулам:

Вычисление начинается с того, что устройство управления выставляет в адресный порт микросхемы памяти SRAM начальный адрес, с которого в .bmp файле хранятся пиксельные данные, как было сказано выше, значение начального адреса — 36h. В файлах .bmp по этому адресу хранится значение синей цветовой компоненты самого нижнего правого пикселя изображения. По адресу 37h — значение зелёной цветовой компоненты, далее красной, потом снова идёт синяя компонента следующего пикселя в самой нижней строке изображения и т. д. Как видно из функциональной схемы, под каждую цветовую компоненту в схеме предусмотрен свой регистр. После загрузки с памяти всех трёх цветовых компонент в свои регистры, со следующего такта генератора осуществляется запись в память результатов вычислений. Так, по адресу синей компоненты «B» записывается монохроматическая красная компонента «Cr», по адресу зелёной компоненты «G» записывается монохроматическая синяя компонента «Cb», и по адресу компоненты «R» записывается компонента яркости «Y». В результате выполнения данного этапа на месте исходного изображения в памяти SRAM, представленного в формате RGB, появится то же изображение в формате YCbCr.
Для аппаратной реализации вычислений яркостной и монохроматических компонент, все дробные коэффициенты из формул были представлены в виде шестнадцатиразрядных слов в формате с фиксированной точкой, где в старших восьми битах содержится целая часть, соответственно в младших восьми — дробная. Например, коэффициент 0.257 в двоичном представлении с фиксированной точкой выглядит так: 0000000001000001 или в шестнадцатиричной форме 0041h. Ограниченность количества разрядов уменьшает точность, так, если дробное двоичное число 0000000001000001 перевести в десятичную форму, то получим: 2^(-2) + 2^(-8) = 0.25 + 0.00390625 = 0.25390625. Как видно, результат отличается от значения 0.257 и для повышения точности представления нужно увеличивать количество разрядов, отводимых под дробную часть. Но я решил ограничиться, как было сказано выше, восемью разрядами.
Итак, на первом этапе преобразования, восьмиразрядные значения цветовых компонент RGB преобразуются в шестнадцатиразрядные в формате с фиксированной точкой путём добавления восьми младших разрядов, заполненных нулевыми битами:

На втором этапе осуществляются операции умножения, сложения и/или вычитания. В результате которых получаются тридцатидвухразрядные данные, где в шестнадцати старших разрядах содержится целая часть, в шестнадцати младших — дробная.
На третьем этапе из полученных тридцатидвухразрядных слов формируются восьмиразрядные данные путём выделения восьми разрядов, стоящих непосредственно перед запятой (если порядковый номер самого младшего бита — 0, а самого старшего — 31, то это биты с 23 по 16):
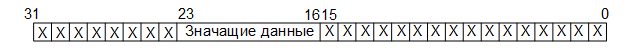
На четвёртом этапе, к полученным восьмиразрядным словам, в соответствии с вышепредставленными формулами, прибавляются смещения (для компоненты Y — 16, для компонент Cb, Cr — 128).
Преобразование из YCbCr в RGB осуществляется по таким формулам:
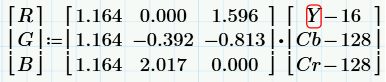
Здесь есть такая особенность, что результаты вычислений, в некоторых случаях, могут приобретать значения большие 255, что выходит за пределы одного байта, либо отрицательные значения, соответственно такие ситуации нужно отслеживать.
Так, если возникает переполнение, то значение итоговой цветовой компоненты должно быть равным 255, для этого просто проводим побитовую логическую операцию «ИЛИ» результата с битом переполнения. А если знаковый разряд результата равен единице (т.е. значение меньше нуля), то значение итоговой цветовой компоненты должно быть равным 0, для этого проводим побитовую логическую операцию «И» результата с инвертированным значением знакового бита.
Итак, на первом этапе операции преобразования цветового пространства YCbCr в RGB, считанные с микросхемы памяти SRAM, восьмиразрядные значения яркостной и монохроматических компонент переводим в дополнительный десятиразрядный код, путём добавления двух старших нулевых бит (знаковый бит и признак переполнения). В итоге получаем десятиразрядные слова. Далее в соответствии с формулами отнимаем от данных значений смещения (или прибавляем отрицательные значения смещений, представленные в десятиразрядном дополнительном коде). Затем, полученный результат переводим из дополнительного кода в прямой, сохраняя значения самого старшего (знакового) бита. Оставшиеся девятиразрядные слова преобразуем в восемнадцатиразрядные с фиксированной точкой путём, приписывания младших девяти разрядов с нулевыми битами:

Дробные коэффициенты, фигурирующие в формулах, также представляем в виде восемнадцатиразрядного кода с фиксированной точкой, где под целую и дробную части отводятся по 9 бит. В результате операций умножения получаем тридцатишестиразрядные значения произведений, в которых 18 старших разрядов – целая часть, 18 младших – дробная. Затем вычисляем знак произведения путём проведения логической операции «сложение по модулю 2», ранее сохранённого знакового разряда со знаком, стоящим перед коэффициентом в формуле (если «-», то «1», если «+», то «0»).
Также нужно определить, не является ли результат произведения нулевым, если результат умножения равен нулю, то и в знаковом разряде должен быть записан 0 вне зависимости от знаков, стоящих перед коэффициентами и знаков, стоящих перед результатами, полученных в результате смещения считанных с памяти компонент. Для этого, к произведению применяем оператор редукции (|product[35:0]), который определяет, все ли биты в результате умножения равны нулю (если да, то результат работы данного оператора будет нулевым), после чего проводим операцию логического «И» полученного результата с результатом операции «сложение по модулю 2» знаковых разрядов.
После всего этого переводим результаты умножения в дополнительный тридцатисемиразрядный код, где в самом старшем разряде хранится знак, и проводим операции сложения. После операций сложения, полученные, в дополнительном коде, результаты переводим в прямой код, и выделяем восемь бит, стоящих непосредственно перед запятой (если номер самого младшего бита 0 а самого старшего – 36, то это биты с 25 по 18). Далее проверяем, не было ли переполнения, для этого, как было сказано выше, проводим операцию побитового логического «ИЛИ» выделенных восьми бит с признаком переполнения, который хранится в 26-ом разряде. И ещё, проверяем не получился ли отрицательный результат, для чего проводим побитовую операцию логического «И» инвертированного знакового разряда с этими же восемью битами:
Полученные, в результате вычисления по трём формулам, и преобразованные восьмиразрядные значения и есть значения цветовых компонент RGB.
Тестировать работу устройства я решил при помощи фотографии Лены Содерберг размером 256 на 256 пикселей:

С этой фотографией работают все, кто занимается обработкой изображений, и я решил не быть исключением.
Итак, в результате преобразования исходной фотографии, загруженной по UART в память SRAM отладочной платы, из цветового пространства RGB в пространство YCbCr, было получено следующее изображение:

Ниже на рисунке справа представлена исходная фотография, слева фотография – результат обратного преобразования из пространства YCbCr в цветовое пространство RGB так, как это описывалось выше:

При сравнении исходной и преобразованной фотографии можно увидеть, что исходная фотография ярче обработанной, это объясняется потерей данных, которые возникали при округлении («отбросе» дробной части), а также потерей точности, при представлении дробных коэффициентов в двоичной форме.
Базовые преобразования и квантование коэффициентов
Дискретное косинусное преобразование
Информации о том, что такое дискретное косинусное преобразование (далее по тексту ДКП), на просторах интернета присутствует в предостаточном количестве, поэтому на теории остановлюсь кратко.
Как было сказано в этой публикации, суть любого базового преобразования сводится к умножению матрицы преобразования на матрицу исходных данных, после чего полученный результат снова умножается уже на транспонированную матрицу того же преобразования. В случае с дискретным косинусным преобразованием, коэффициенты матрицы преобразования вычисляются по следующему правилу:
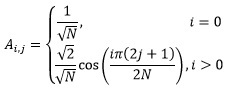
Где:
N — размерность матрицы;
i, j — индексы элементов матрицы.
В нашем случае N = 8, т.е. исходное изображение разбивается на блоки 8 на 8 пикселей, при этом значения индексов i и j изменяются в диапазоне от 0 до 7.
В результате применения этого правила при N = 8 получаем такую матрицу преобразования:
Для того, чтобы не проводить вычисления с дробными числами помножим каждый элемент матрицы на 8v8, и округлим полученные значения элементов матрицы до целых чисел, в результате чего получим матрицу Т:
При этом, необходимо будет результат умножения матриц, как в случае прямого дискретного косинусного преобразования при кодировании, так и в случае обратного при декодировании, разделить на 512. Учитывая, что 512 = 2^(9), то деление осуществляется методом сдвига делимого вправо на 9 позиций.
В результате прямого дискретного косинусного преобразования получается матрица, так называемых, коэффициентов ДКП, в которой элемент, расположенный в нулевой строке и нулевом столбце, называется низкочастотным коэффициентом и его значение всегда положительное. Остальные элементы матрицы ДКП – высокочастотные коэффициенты, значения которых могут быть как положительными, так и отрицательными. Учитывая это, и то, что элементы результирующей матрицы должны быть восьмиразрядными, для низкочастотного коэффициента диапазон значений составит [0..255], а для высокочастотных – [-127..127]. Для того, чтобы уложиться в эти диапазоны необходимо результаты прямого дискретного косинусного преобразования разделить на 8, соответственно результаты обратного – помножить на 8. В результате для прямого ДКП получаем такую формулу:
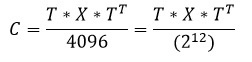
Где:
С – матрица коэффициентов дискретного косинусного преобразования;
Т – матрица преобразования;
Х – матрица 8 на 8 яркостной или монохроматических компонент (в зависимости от того какая, назовём так, компонентная плоскость Y, Cb или Cr кодируется).
Для обратного ДКП получаем следующую формулу:
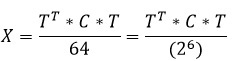
Коэффициенты матрицы T в восьмиразрядном формате хранятся в памяти ROM, расположенной на кристалле ПЛИС в прямом коде, при этом старший бит содержит знак.
И так, на первом этапе дискретного косинусного преобразования, с памяти SRAM в операционный блок, осуществляющий прямое ДКП, последовательно считываются 64 байта одной из компонент (сначала кодируется вся компонентная плоскость Y, затем Cb и Cr), образующие часть изображения, как было написано ранее, размером 8 на 8 пикселей (при этом адреса для памяти SRAM генерируются особым образом):

Операции вычисления в данном блоке осуществляются с двадцатиодноразрядными данными: 12 младших разрядов – значения, которые будут потерянны при делении на 4096 (2^(12)), 8 разрядов – значащая часть и старший разряд – знак, итого: 12+8+1 = 21:
Исходя из этого, во время загрузки, восьмиразрядные данные в операционном блоке преобразуются в двадцатиодноразрядные слова, представленные в дополнительном коде, путём приписывания старших тринадцати разрядов, заполненных нулевыми битами (старший бит — знак), после чего полученное слово запоминается в буферную память RAM, расположенную, также, на кристалле ПЛИС, в адресное пространство c 00h по 3Fh (среда Quartus II не позволила создать память RAM с организацией 128х21, поэтому пришлось использовать память с организацией 128х32).
На втором этапе, после того как в буферную память RAM записано 64 двадцатиодноразрядных слова (блок 8 на 8), запускается процесс умножения матриц. При этом, с памяти ROM считывается восьмиразрядный строковый элемент матрицы преобразования, который «разворачивается» в двадцатиодноразрядное слово, путём записывания седьмого (знакового) бита значения, считанного с памяти ROM, в двадцатый (знаковый) бит распакованного слова. Остальные семь бит, считанного восьмиразрядного значения элемента матрицы преобразования, переписываются в семь младших бит распакованного слова, биты с порядковыми номерами 7 – 19 заполняются нулями:

Далее, с буферной памяти RAM считывается, ранее записанный туда, двадцатиодноразрядный столбцовый элемент, после чего, его двадцать младших разрядов перемножаются с двадцатью разрядами развёрнутого элемента матрицы преобразования. Знак произведения вычисляется также, как и при преобразовании цветовых пространств:

Произведение переводится в дополнительный код и запоминается в стек, глубиной 8 двадцатиодноразрядных слов. Как только стек заполнен (это означает, что элементы строки матрицы преобразования перемножены на элементы очередного столбца исходной матрицы), все значения стека суммируются и результат в дополнительном коде, записывается в буферную память RAM, в адресное пространство с 40h по 7Fh.На третьем этапе, с буферной памяти RAM, с адресного пространства 40h – 7Fh, построчно считываются элементы матрицы, которая является результатом произведения матриц преобразования и исходной матрицы, и преобразуются в прямой код. А с памяти ROM, также как и ранее, считываются, также построчно, и разворачиваются элементы матрицы преобразования (вопреки правилу умножения матриц, здесь мы перемножаем строку на строку, что означает операцию транспонирования матрицы множителя). Затем, также как и раньше, в прямом коде перемножаются двадцатиразрядные элементы матриц, вычисляется знаковый разряд, произведение переводится в дополнительный код и запоминается в стек. Как только стек заполняется восемью элементами, осуществляется их суммирование, и результат из дополнительного кода переводится в прямой.
Далее осуществляется операция квантования. Каждый элемент полученной матрицы делится на, так называемый, соответствующий коэффициент квантования, таблица которых хранится в отдельной памяти ROM на кристалле ПЛИС. Значения коэффициентов квантования рассчитывались по следующей формуле:
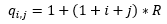
Где:
R – коэффициент сжатия, или коэффициент характеризующей потери качества восстановленным изображением по отношению к исходному;
i, j – индексы вычисляемого элемента матрицы квантования, изменяются в пределах от 0 до 7.
Тут же нужно сказать, что для всех компонентных плоскостей Y, Cb, Cr в кодеке используется одна матрица квантования, вычисленная для R = 2 (не стал я заморачиваться, делая для каждой плоскости свою таблицу коэффициентов квантования).
Для того, чтобы аппаратно не реализовывать делитель, операцию деления при квантовании я заменил операцией умножения следующим образом:
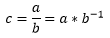
Где:
a – квантуемый коэффициент, элемент результативной матрицы базового преобразования;
b – соответствующий коэффициент матрицы квантования, вычисленный по ранее приведённой формуле;
c – результат квантования.
Соответственно, в память ROM записаны результаты возведения в степень -1 (или 1/b), представленные в формате с фиксированной точкой, при этом в памяти хранятся только 8 разрядов дробной части, так как целая часть всегда равна 0.
Процесс квантования в кодеке реализован следующим образом: как только вычислен и переведён из дополнительного кода в прямой, очередной двадцатиодноразрядный элемент результирующей матрицы линейного преобразования, определяется, является ли этот элемент низкочастотным коэффициентом и если да, разряды с 19 по 12 записываются в восемь старших разрядов промежуточного шестнадцатиразрядного регистра, 8 младших разрядов данного регистра, при этом, заполняются нулями (разряды с 11 по 0 исходного двадцатиодноразрядного слова отбрасываются, так осуществляется операция деления на 4096).
Если элемент является высокочастотным коэффициентом, то в самый старший разряд промежуточного регистра записывается 0, в семь следующих разрядов переписываются разряды с 18 по 12 двадцатиодноразрядного слова, а 8 младших разрядов промежуточного регистра, также, заполняются нулями. Выходы с данного промежуточного регистра подключены к одному из входных портов умножителя 16х16, на другой порт данного умножителя подаются значения из памяти ROM, где хранятся дробные части коэффициентов квантования, возведённых в степень -1. Причём, на 8 старших выводов порта подаются нулевые значения, а на 8 младших – значения считанные с памяти ROM.
Далее, с тридцатидвухразрядного выходного порта умножителя считывается результат квантования, в котом 16 младших разрядов – дробная часть, которая отбрасывается, а 8 разрядов, стоящих непосредственно перед фиксированной запятой, это значащая часть (я думаю и так понятно, что результат квантования – это дробное число, представленное в формате с фиксированной точкой). Причём, в случае с низкочастотными коэффициентами, значащей частью являются не 8, а 7 разрядов, стоящих непосредственно перед запятой, в восьмой разряд здесь переписывается знак, полученный ещё на этапе базового преобразования, находящийся в самом старшем разряде:
Ну и далее, сформированные восьмиразрядные значения записываются в буферную память RAM в адресное пространство 00h – 3Fh:

Готовые данные с буферной памяти считываются в соответствии с алгоритмом зигзаг-сканирования (что такое зигзаг-сканирование можно прочитать здесь) и идут на этап кодирования длин серий.
Декодирование идёт в обратном порядке. И здесь мы оперируем уже пятнадцатиразрядными данными: 6 младших разрядов – разряды, которые теряются при делении на 64, 8 разрядов – значащая часть, 1 разряд – знак. Итого: 6+8+1 = 15:
На первом этапе, поступившее в операционный блок, осуществляющий обратное дискретное косинусное преобразование, восьмиразрядное слово разворачивается до пятнадцатиразрядного. Для это, сначала осуществляется проверка, не является ли поступивший байт низкочастотным коэффициентом, и если да, то все 8 разрядов переписываются в 8 младших разрядов пятнадцатиразрядного слова. А если поступил высокочастотный коэффициент, то 7 младших разрядов поступившего байта переписываются в 7 младших разрядов пятнадцатиразрядного слова, а старший разряд, содержащий знак, записывается в самый старший разряд пятнадцатиразрядного слова.
Затем развёрнутые до 15-ти разрядов данные записываются в буферную память RAM в адресное пространство 00h – 3Fh в соответствии с алгоритмом зигзаг-сканирования. После того как в памяти RAM будет сформирована матрица квантованных коэффициентов ДКП размером 8 на 8, начинается процесс обратного дискретного косинусного преобразования, также как было описано выше. При этом каждое считанное пятнадцатиразрядное слово с RAM, сначала проходит процедуру восстановления (процедура обратная квантованию) путём умножения на соответствующий коэффициент квантования, хранящийся в памяти ROM.
Здесь осуществляется умножение четырнадцатиразрядного слова на восьмиразрядный коэффициент квантования, который является целым числом (это те значения, которые при сжатии возводились в степень -1). Далее осуществляется перемножение матриц также, как было описано выше. После чего из получившихся пятнадцатиразрядных значений отбрасываются 6 младших разрядов (деление на 64) и проверяется знаковый разряд, и если его значение равно 0, то 8 последующих разрядов содержат результирующее значение декодируемой компоненты Y, Cb или Cr (в зависимости от того, какая компонентная плоскость декодируется). А если знаковый разряд равен 1, то следующие 8 разрядов просто обнуляются (т.е. округляются до 0, т.к. результат обратного ДКП не может быть отрицательным).
Получаемые восьмиразрядные результаты обратного ДКП записываются в буферную память RAM, формируя, таким образом, блок изображения 8 на 8. После того как блок сформирован, каждый его элемент переписывается во внешнюю память SRAM по соответствующему адресу, формируя там, в свою очередь, конечное изображение в пространстве YCbCr.
Преобразование Уолша
И вот, наконец-то мы дошли до того, ради чего всё затевалось. Преобразование Уолша – разновидность базового преобразования, матрица преобразования которого выглядит следующим образом:

Информацию о том, откуда эта матрица берётся, как выводится и как формируется, можно, также, найти в интернете или в учебниках по теории цепей и сигналов. Останавливаться здесь на этом не будем.
Итак, как было сказано выше, базовое преобразование сводится к умножению матрицы преобразования на матрицу исходных данных, после чего полученный результат снова умножается уже на транспонированную матрицу того же преобразования. Значения всех элементов матрицы преобразования Уолша равны либо 1, либо -1, соответственно аппаратно потребуется выполнять только операции сложения данных, представленных в дополнительном коде. Если расписать процесс умножения матрицы Уолша на исходную матрицу блока изображения 8 на 8, то получим следующие выражения для каждого строкового элемента промежуточной матрицы:
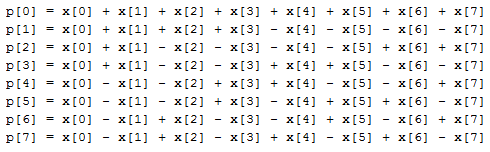
Где:
p[0..7] — очередная строка промежуточной матрицы;
x[0..7] — очередная строка исходной матрицы, являющейся блоком изображения 8 на 8.
И далее, если расписать процесс умножения промежуточной матрицы на транспонированную матрицу Уолша, то получим такие выражения для каждого уже столбцового элемента результирующей матрицы:

Где:
y[0..7] — очередной столбец результирующей матрицы;
p[0..7] — очередной столбец промежуточной матрицы.
Также как и в случае с ДКП, верхний левый элемент результирующей матрицы, будет являться низкочастотным коэффициентом, значение которого всегда больше 0, а остальные 63 элемента — высокочастотные коэффициенты, значения которых могут быть как меньше так и больше 0 (также как и при ДКП).
Аппаратно, блок преобразования Уолша, представляет собой группу сумматоров подключённых определённым образом, на входы которых сначала поочерёдно подаются строки исходной матрицы, результаты при этом запоминаются в буфер, а затем из буфера на входы этой же группы сумматоров поочерёдно подаются столбцы, ранее полученной матрицы. Также нужно учесть, что при прямом преобразовании Уолша, значения элементов результирующей матрицы могут выходить за пределы 255, поэтому их нужно будет разделить на 64 или сдвинуть на 6 разрядов вправо.
Обратное преобразование Уолша осуществляется точно также с тем лишь исключением, что элементы результирующей матрицы, которая будет являться блоком изображения 8 на 8 не нужно не на что делить, значения уже получаются нормированными.
Итак, в блоке прямого преобразования Уолша поступающие восьмиразрядные значения компонент, по аналогии с блоком ДКП, разворачиваются в пятнадцатиразрядные (6 разрядов — разряды которые будут потеряны при делении на 64, 8 разрядов — значащие разряды, 1 разряд — знак) и записываются в буферную память RAM. Как только в буфере сформирована матрица 8 на 8, из буфера построчно считываются элементы исходной матрицы, преобразуются, и записываются в адреса той же строки, откуда были считаны. Это позволяет использовать память RAM c организацией 64х15 (в случае с ДКП потребовался буфер с организацией 128х21), но Quartus II позволил создать блок памяти RAM только с организацией 64х16, один разряд остался не использованным (хотя в случае с ДКП не использовалось 11 разрядов).
Затем из буфера считываются уже столбцы матрицы, полученной на предыдущем этапе, преобразуются, и результат этого преобразования переводится из дополнительного кода в прямой, после чего абсолютно также, как и в случае прямого ДКП осуществляется операция квантования, результат которой записывается в буферную память RAM откуда, затем считывается в соответствии с алгоритмом зигзаг-сканирования. Обратное преобразование Уолша осуществляется аналогично прямому, поступающие данные при этом записываются в буферную память RAM в по алгоритму зигзаг-сканирования, а при считывании для непосредственного преобразования Уолша, домножаются на соответствующие коэффициенты квантования.
Ниже, в сравнительной форме, представлены результаты работы блоков прямого преобразования Уолша и прямого дискретного косинусного преобразования:

Сверху слева представлена фотография, на которой мы тренируемся, которая сначала была переведена, скажем так, внутри нашей отладочной платы, из цветового пространства RGB в пространство YCbCr, затем каждая компонентная плоскость была разбита на блоки 8 на 8 и преобразована по правилу прямого преобразования Уолша. Сверху справа та же фотография, преобразованная по правилу прямого ДКП. Снизу слева результат преобразования Уолша, подвергнутый операции квантования, соответственно, снизу справа, подвергнутый операции квантования, результат прямого ДКП, считанные с отладочной платы.
Кодирование длин серий
Алгоритм кодирования длин серий ещё, по-другому, называют алгоритмом сжатия, использующим исключение повторов (RLE – Run Length Encoding). В основе данного алгоритма лежит принцип определения групп одинаковых, идущих подряд символов (байт с одинаковыми значениями), и заменой их определённой структурой, содержащей количество повторов и код повторяющихся символов, т.е. <количество повторов><повторяющийся символ (байт)>. Очевидно, что максимальное количество одинаковых символов (байт данных), которые можно закодировать такой структурой, зависит от длины кода количества повторов.
Для реализации, решено было выбрать алгоритм, который реализован в графическом формате .pcx. В этом алгоритме RLE особенность в том, что количество повторов кодируется байтом-счётчиком, в котором старшие два бита содержат единицы, а младшие шесть содержат количество повторов. Соответственно значения байт, которые подряд не повторяются и значения которых меньше С0h переписываются в поток сжатых данных без изменения. А не повторяющиеся подряд значения байт большие C0h, (две единицы в старших разрядах), при записи в выходной поток, в любом случае, предваряются байтом счётчиком, и, так как такой символ в потоке один, то и байт счётчик принимает значение С1h. Также нужно учитывать, что максимальное число повторов, которое можно закодировать в шести выделяемых битах, составляет 63=3Fh, поэтому, после каждого увлечения счётчика повторов, нужно проверять, не составило ли его значение 63, и если да, в выходной поток, сначала, нужно выставить значение FFh (C0h(префикс байта-счётчика)+3Fh(количество повторов) = FFh), а затем значение повторяющегося байта, после чего счётчик обнуляется и подсчёт начинается снова.
Например, на выходе блока базового преобразования (будь то блок прямого ДКП или быстрого преобразования Уолша) имеем следующий поток данных, выдаваемых с буферной памяти RAM в соответствии с алгоритмом зигзаг-сканирования: ECh, C2h, 03h, 0Ah, 0Ah, D1h, D1h, 01h, 01h, 01h, 00h, 00h, 00h, 00h, 00h, 02h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h. Тогда, после кодирования данного потока, алгоритмом RLE, получим следующий поток данных: C1h, ECh, C1h, C2h, 03h, C2h, 0Ah, C2h, D1h, C3h, 01h, C5h, 00h, 02h, F0h, 00h.
Итого, в нашем случае, из строки длинной 64 байта, после сжатия получена строка длинной 16 байт, в которой наибольшее количество повторов принадлежит нулевым байтам. Эти нулевые байты и есть, округленные до нуля после квантования, высокочастотные коэффициенты, соответственно, если квантование не проводить, то количество подряд идущий нулевых байт будет значительно ниже, что даст более низкую степень сжатия, но позволит сохранить качество изображения.
Аппаратно, данный алгоритм реализуется довольно-таки просто как при сжатии так и при распаковке.
При распаковке после получения очередного байта, проверяем его старшие два бита, и если их значения равны единице, то младшие шесть байт загружаем в счётчик, считываем последующий бай, не проверяя его старших бит, выставляем его в выходной поток, декрементируя, при этом, счётчик до тех пор, пока он не обнулится, после чего читаем следующий байт с потока, а если же значения старших бит счётчика отличны от двух единиц, то переписываем этот байт в выходной поток без изменений.
В кодеке, кодирующий алгоритм RLE выполняется устройством управления во время считывания байт данных с блока базового преобразования при сжатии, декодирующий алгоритм RLE, выполняется перед загрузкой данных в блок базового преобразования при распаковке (я думаю, это и так понятно).
Сжатие по алгоритму Хаффмана
Алгоритму Хаффмана была посвящена не одна статья, опубликованная на этом сайте, поэтому, также как и ранее, на теории останавливаться не буду. Скажу лишь то, что по аналогии с алгоритмом JPEG, в описываемом здесь устройстве, я реализовал алгоритм Хаффмана с, заранее вычисленными, фиксированными таблицами.
Отличие от алгоритма JPEG в том, что в JPEG в таблицах хранятся только длины кодов, а не сами коды, в рассматриваемом же устройстве, в одной памяти ROM отдельно хранятся шестнадцатиразрядные коды Хаффмана, а в другой памяти ROM, хранятся количества значащих бит в каждом из шестнадцатиразрядных кодов, начиная с самого старшего. Также в JPEG для низкочастотных и высокочастотных коэффициентов используются разные таблицы, и вместо самих значений низкочастотных коэффициентов, кодируются их разности. В своём же устройстве я всё так усложнять не стал (может быть зря) и, в разработанном мной устройстве, все коэффициенты кодируются единым потоком и единой таблицей.
Кодирование осуществляется так: на адресные входы блоков памяти ROM, подаются кодируемые байты (поток данных, закодированных по алгоритму RLE), при этом, с выхода блока памяти ROM, где хранятся коды Хаффмана, считывается то количество бит, значение которого было считано с выхода другого блока памяти ROM. Коды Хаффмана и их длины хранятся по тем адресам, значения которых соответствует значениям кодируемых байт.
Далее, из считываемого потока бит, формируются байты и записываются в память. Например, при кодировании одного байта, с памяти ROM, содержащей код Хаффмана, было считано 4 бита, при кодировании второго байта в потоке – 11 бит, третьего – 3, и четвёртого – 4. Итого, получаем 4+11+3+4 = 22, 22 бита делим на 8 получаем 2 байта и 6 бит, к которым дописываем, в младшие разряды, два нулевых бита (так кодируется самый последний байт в потоке) и получаем 3 равноценных байта, которые и записываются во внешнюю память, т.е. из четырёх байт на входе получили три на выходе.
Декодер Хаффмана реализован в виде таблицы истинности, на языке AHDL (в данном языке предусмотрен для этого специальный оператор “TABLE”, хотя, можно было это сделать и на языке Verilog при помощи оператора “case”, кому как больше нравится), у которой один шестнадцатиразрядный входной порт, для кода Хаффмана и один пятиразрядный входной порт для длины этого кода.
Декодирование осуществляется так: с внешней памяти SRAM считывается байт, который побитно загружается в шестнадцатиразрядный регистр, начиная со старшего разряда, выходы которого подключены к шестнадцатиразрядному входному порту Декодера Хаффмана (той самой таблицы), после загрузки очередного бита, осуществляется инкрементирование счётчика, подключенного к другому порту декодера Хаффмана.
После загрузки очередного бита, проверяется сигнал, означающий, что входной комбинации кода Хаффмана и длины кода, найден выходной байт, и если значение данного сигнала равно логической единице, то с выходного порта декодера Хаффмана считывается байт, который идёт на декодирование по алгоритму RLE. При этом шестнадцатиразрядный регистр обнуляется, а оставшиеся в байте биты загружаются в него вновь со старшего разряда, если биты в считанном с внешней памяти байта закончились, то считывается новый байт и т.д.
Проверка работы кодека в комплексе
На первом этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе быстрого преобразования Уолша, с квантованием коэффициентов. В итоге, загруженное по UART в устройство, наше тестовое изображение размером 256 на 256 точек с объёмом занимаемой памяти 192 Кбайта, было преобразовано (сжато) в файл с объёмом занимаемой памяти 8,1 Кбайт.
На втором этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе быстрого преобразования Уолша, но без квантования коэффициентов. В итоге, то же изображение было преобразовано (сжато) в файл с объёмом занимаемой памяти 43,8 Кбайт.
На третьем этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе дискретного косинусного преобразования, с квантованием коэффициентов. В итоге, загруженное по UART в устройство, наше тестовое изображение размером 256 на 256 точек с объёмом занимаемой памяти 192 Кбайта, было преобразовано (сжато) в файл с объёмом занимаемой памяти 8,17 Кбайт.
На четвёртом этапе был скомпилирован и прошит в ПЛИС кодер, осуществляющий сжатие на базе дискретного косинусного преобразования, уже без квантования коэффициентов. В итоге, то же изображение было преобразовано (сжато) в файл с объёмом занимаемой памяти 35,9 Кбайт.
Ниже представлены результаты распаковки, разработанным устройством, ранее сжатых изображений.
На рисунке, представленном ниже, в центре показано исходное изображение, слева – изображение, сжатое с квантованием коэффициентов, при помощи быстрого преобразования Уолша, справа – изображение, сжатое с квантованием коэффициентов, при помощи дискретного косинусного преобразования:

Разницу в базовых преобразованиях отчётливо при увеличении одинаковых участков изображений. Так, преобразование Уолша даёт более контрастные границы на участках переходов, в свою очередь, ДКП делает переходы на границах более плавными.
Ниже представлены результаты распаковки изображений, которые сжимались без квантования коэффициентов. Также как и в предыдущем случае, в центре — исходное изображение, слева – изображение, сжатое при помощи быстрого преобразования Уолша, справа – при помощи ДКП:

На первый взгляд, особых потерь в качестве нет, но если изображения увеличить, то можно увидеть, границы блоков 8 на 8, которые, в случае преобразования Уолша, также имеют более контрастные границы, а случае с ДКП – более плавные. Вообще, касательно вопросов оценки качества изображений написан целый ряд работ, и заниматься здесь этим не очень хочется.
Подведение итогов
И так, ниже представлена таблица, содержащая результаты определения характеристик сжатия, полученных на разработанном устройстве, изображения, размером 256 на 256 пикселей представленного в формате .bmp с объёмом занимаемой памяти (Lисх.) 192 КБайта. Размер исходного изображения вычисляется так: 256?256 = 65536 точек, на каждую точку приходится по три байта (1 байт – красная компонента, 1 байт – зелёная компонента, 1 байт – синяя компонента), получаем 65536?3 = 196608 байта, плюс ещё 53 байта – заголовок, итого получаем 196661 байт или 196661/1024 ? 192 КБайта с «копейками»:

Из таблицы видно, что оба способа базового преобразования в аппаратной реализации, дают, практически, одинаковые результаты, за исключением времени и скорости сжатия/распаковки. Здесь преобразование Уолша выигрывает у частного случая преобразования Фурье — ДКП. 1 — 0 в пользу преобразования Уолша.
Если сравнивать оба вида преобразования с точки зрения затрат аппаратных ресурсов ПЛИС, то получим следующее:
Из представленных скриншотов видно, что аппаратных ресурсов ПЛИС, оба преобразования потребляют одинаково, за исключением использования встроенных умножителей. Здесь частный случай преобразования Фурье снова проиграл преобразованию Уолша. Итого: 2 — 0 в пользу преобразования Уолша.
В принципе, можно сделать такой вывод, что с очки зрения аппаратной реализации лучше использовать, в качестве базового преобразования, преобразование Уолша.
Ну и в самом заключении хочется отметить, что данный аппаратный кодек сжатия/распаковки изображений, разрабатывался, скажем так, необдуманно и непродуманно. Именно этим и объясняется неудовлетворительные (по крайней мере, мне так показалось) значения временных характеристик сжатия/распаковки. Просматривая проект снова и снова, я всё время нахожу возможности оптимизации и варианты уменьшения времени обработки изображения, с одновременным увеличением размера, обрабатываемого (сжимаемого/распаковываемого) изображения. В итоге, можно будет добиться скорости сжатия/распаковки — 24 изображения в секунду, что позволит обрабатывать видео потоки.
Ну вот, на этом всё. Спасибо за внимание!


mkarev
Киллер фича преобразования DCT-II, используемого в алгоритмах сжатия изображений, заключается в том, что большая часть энергии входного сигнала сосредоточена в области низких частот (левый верхний угол). Это позволяет заквантовывать в хлам высокие частоты и получать после прохода зигзагом большие серии нулей. Которые затем эффективно кодируются алгоритмом RLE и далее Хаффманом. Преобразование Уолша, на сколько мне известно, такими свойствами не обладает.
Для объективного сравнения двух кодеков можно сделать следующее: закодировать спроектированным и референсным(JPEG) кодеками серию картинок с увеличивающимися квантизациями и посчитать искажения (PSNR). Затем, для каждого кодека построить график зависимости PSNR от размера изображения.
Если разработанный Вами кодек будет иметь кривую PSNR(Bitrate), совпадающую с аналогичной кривой JPEG, то можно сказать что потери качества нет.
Если график будет над JPEG (при одинаковом размере файла — меньшее искажение), то надо срочно патентовать.
Если график будет ниже JPEG, то очевидно имеем просадку качества (на том же самом битрейте бОльшие искажения).