В финансах есть задачи по оценке инвестиционных проектов, в которых находится целый ряд показателей по значениям которых даётся общая оценка. Это такие показатели как срок окупаемости проекта, приведённый доход, чистый приведённый доход и т. д. Как правило, для определения каждого из показателей существуют свои формулы, в которые, просто, нужно подставить исходные данные, вычислить и получить результат. Но есть один из показателей, который простой подстановкой данных в формулу не решается. Этот показатель называется "внутренняя норма доходности". В настоящее время существует большое множество различного программного обеспечения для финансистов, которое позволяет вести все вычисления автоматически, не задумываясь о том, как всё происходит внутри.
Итак, предположим нам дана таблица, в которой приведены данные некоторого инвестиционного проекта:

Где:
C — первоначальные инвестиции (величина всегда отрицательная);
Vj — финансовые поступления от реализации проекта в j-ом периоде;
j — порядковый номер периода (календарного года).
Также нам дана процентная годовая ставка дисконтирования — i.
Нам нужно определить внутреннюю норму доходности данного проекта — IRR.
Внутренняя норма доходности вычисляется так: нужно подобрать такое значение процентной ставки IRR, чтобы решилось уравнение:

В нашем случае, первоначальные вложения (инвестиции) в проект осуществлялись только один раз, согласно заданной таблице — в нулевой год, соответственно, выше представленное уравнение примет следующий вид:

Для определения внутренней нормы доходности, ещё понадобится формула определения общего чистого приведённого дохода (NPV) для пяти периодов финансовых поступлений:

Где PVj — приведённый доход за j-ый период:

Если заменить выражением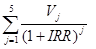 выражение
выражение  в формуле определения приведённого дохода PV, которую затем подставить в формулу определения общего чистого приведенного дохода NPV, то получим следующую функцию:
в формуле определения приведённого дохода PV, которую затем подставить в формулу определения общего чистого приведенного дохода NPV, то получим следующую функцию:

Если заменим искомую величину IRR при которой на величину процентной ставки r которая меняется на интервале от 0 до 100% то получим функцию:
на величину процентной ставки r которая меняется на интервале от 0 до 100% то получим функцию:

график которой представлен на рисунке ниже:

Из графика видно, что задача поиска внутренней нормы доходности IRR (NPV(IRR)=0) сводится к поиску точки пересечения графика с осью абсцисс, которую можно найти любым из численных методов.
Возьмём, для примера, численный метод Ньютона. Имея данные, из заданной таблицы, составим степенную функции одной переменной x для инвестиционного проекта:

Последовательность приближения к значению множителя дисконтирования строится от начального значения x0=1 по следующей формуле:

Где:
k — номер шага итерации;
 — производная от степенной функции:
— производная от степенной функции:

Каждое вновь вычисленное значение xk подставляется в формулу (данная формула выводится из формулы определения дисконта), затем каждое вновь вычисленное значение rk, в свою очередь, подставляется в формулу
(данная формула выводится из формулы определения дисконта), затем каждое вновь вычисленное значение rk, в свою очередь, подставляется в формулу  . Последовательность приближений осуществляется до тех пор, пока не будет достигнута заданная точность, т. е. подбор значения множителя дисконтирования xk осуществляется до тех пор, пока не выполнится условие f(rk) ? ?, где ? – заданная точность (например 0,001). Значение rk при котором выполнится неравенство и есть искомая внутренняя норма доходности IRR.
. Последовательность приближений осуществляется до тех пор, пока не будет достигнута заданная точность, т. е. подбор значения множителя дисконтирования xk осуществляется до тех пор, пока не выполнится условие f(rk) ? ?, где ? – заданная точность (например 0,001). Значение rk при котором выполнится неравенство и есть искомая внутренняя норма доходности IRR.
Итак, предположим нам дана таблица, в которой приведены данные некоторого инвестиционного проекта:

Где:
C — первоначальные инвестиции (величина всегда отрицательная);
Vj — финансовые поступления от реализации проекта в j-ом периоде;
j — порядковый номер периода (календарного года).
Также нам дана процентная годовая ставка дисконтирования — i.
Нам нужно определить внутреннюю норму доходности данного проекта — IRR.
Внутренняя норма доходности вычисляется так: нужно подобрать такое значение процентной ставки IRR, чтобы решилось уравнение:

В нашем случае, первоначальные вложения (инвестиции) в проект осуществлялись только один раз, согласно заданной таблице — в нулевой год, соответственно, выше представленное уравнение примет следующий вид:

Для определения внутренней нормы доходности, ещё понадобится формула определения общего чистого приведённого дохода (NPV) для пяти периодов финансовых поступлений:

Где PVj — приведённый доход за j-ый период:

Если заменить выражением
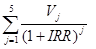 выражение
выражение  в формуле определения приведённого дохода PV, которую затем подставить в формулу определения общего чистого приведенного дохода NPV, то получим следующую функцию:
в формуле определения приведённого дохода PV, которую затем подставить в формулу определения общего чистого приведенного дохода NPV, то получим следующую функцию:
Если заменим искомую величину IRR при которой
 на величину процентной ставки r которая меняется на интервале от 0 до 100% то получим функцию:
на величину процентной ставки r которая меняется на интервале от 0 до 100% то получим функцию:
график которой представлен на рисунке ниже:

Из графика видно, что задача поиска внутренней нормы доходности IRR (NPV(IRR)=0) сводится к поиску точки пересечения графика с осью абсцисс, которую можно найти любым из численных методов.
Возьмём, для примера, численный метод Ньютона. Имея данные, из заданной таблицы, составим степенную функции одной переменной x для инвестиционного проекта:

Последовательность приближения к значению множителя дисконтирования строится от начального значения x0=1 по следующей формуле:

Где:
k — номер шага итерации;
 — производная от степенной функции:
— производная от степенной функции:
Каждое вновь вычисленное значение xk подставляется в формулу
 (данная формула выводится из формулы определения дисконта), затем каждое вновь вычисленное значение rk, в свою очередь, подставляется в формулу
(данная формула выводится из формулы определения дисконта), затем каждое вновь вычисленное значение rk, в свою очередь, подставляется в формулу  . Последовательность приближений осуществляется до тех пор, пока не будет достигнута заданная точность, т. е. подбор значения множителя дисконтирования xk осуществляется до тех пор, пока не выполнится условие f(rk) ? ?, где ? – заданная точность (например 0,001). Значение rk при котором выполнится неравенство и есть искомая внутренняя норма доходности IRR.
. Последовательность приближений осуществляется до тех пор, пока не будет достигнута заданная точность, т. е. подбор значения множителя дисконтирования xk осуществляется до тех пор, пока не выполнится условие f(rk) ? ?, где ? – заданная точность (например 0,001). Значение rk при котором выполнится неравенство и есть искомая внутренняя норма доходности IRR.

