27.04.2020 07:15
SmartEngines 0 450 Источник

(изображение взято отсюда)

Сегодня мы бы хотели вам рассказать о задаче пост-обработки результатов распознавания текстовых полей исходя из априорных знаний о поле. Ранее мы уже писали про метод коррекции полей на основе триграмм, который позволяет исправлять некоторые ошибки распознавания слов, написанных на естественных языках. Однако значительную часть важных документов, в том числе документов, удостоверяющих личность, составляют поля другого характера – даты, номера, VIN-коды автомобилей, номера ИНН и СНИЛС, машинно-читаемые зоны с их контрольными суммами и многое другое. Хотя их нельзя отнести к полям естественного языка, тем не менее у таких полей зачастую существует некоторая, иногда неявная, языковая модель, а значит, для них тоже можно применить некоторые алгоритмы коррекции. В этом посте речь пойдет об двух механизмах пост-обработки результатов распознавания, которые можно применять для большого количества документов и типов полей.

Языковую модель поля можно условно подразделить на три составляющие:
  1. Синтаксис: правила, регулирующие структуру текстового представления поля. Пример: поле “дата окончания срока действия документа” в машинно-читаемой зоне представлятся в виде семи цифр “DDDDDDD”.
  2. Семантика поля: правила, основывающиеся на смысловой интерпретации поля или его составных частей. Пример: в поле “дата окончания срока действия документа” машинно-читаемой зоны первые две цифры – это последние две цифры года, 3-я и 4-я цифры – это месяц, 5-я и 6-я – это день, и 7-я цифра – контрольная сумма.
  3. Семантика связей: правила, основывающиеся на структурной и смысловой связи поля с другими полями документа. Пример: поле “дата окончания срока действия документа” не может кодировать дату, соответствующую более раннему моменту времени, чем поле “дата рождения”.

Располагая информацией о семантической и синтаксической структуре документа и распознаваемого поля, можно построить специализированный алгоритм пост-обработки результата распознавания. Однако, принимая во внимание необходимость поддержки и развития систем распознавания и сложность их разработки, интересно рассмотреть “универсальные” методы и инструменты, которые позволили бы с минимальными усилиями (со стороны разработчиков) построить достаточно хороший алгоритм пост-обработки, который бы работал с обширным классом документов и полей. Методика настройки и поддержки такого алгоритма была бы унифицирована, а изменяемым компонентом структуры алгоритма была бы только языковая модель.

Стоит отметить, что пост-процессинг результатов распознавания текстовых полей не всегда полезен, а иногда даже вреден: в случае, если у вас достаточно хороший модуль распознавания строки и вы работаете в критических системах с документами, удостоверяющими личность, то какой-либо пост-процессинг лучше минимизировать и выдавать результаты “так как есть”, либо четко контролировать любые изменения и сообщать о них клиенту. Однако во многих случаях, когда заведомо известно, что документ действительный, и что языковая модель поля надежна – использование алгоритмов пост-обработки позволяет значительно повысить итоговое качество распознавания.

Итак, в статье пойдет речь о двух методах пост-обработки, претендующих на универсальность. Первый основан на взвешенных конечных преобразователях, требует описания языковой модели в виде конечного автомата, не очень прост в использовании, но более универсален. Второй – более простой в использовании, более эффективен, требует всего лишь написания функции проверки валидности значения поля, но также обладает рядом недостатков.

Метод на основе взвешенных конечных преобразователей


Красивая и достаточно общая модель, позволяющая построить универсальный алгоритм пост-обработки результатов распознавания, описана в этой работе. Модель опирается на структуру данных взвешенных конечных преобразователей (Weighted Finite-State Transducers, WFST).

WFST представляют собой обобщение взвешенных конечных автоматов – если взвешенный конечный автомат кодирует некоторый взвешенный язык L (т.е. взвешенное множество строк над некоторым алфавитом A), то WFST кодирует взвешенное отображение языка L_1 над алфавитом A_1 в язык L_2 над алфавитом A_2. Взвешенный конечный автомат, принимая строку S над алфавитом A, ставит ей в соответствие некоторый вес w, тогда как WFST, принимая строку S_1 над алфавитом A_1, ставит ей в соответствие множество (возможно, бесконечное) пар \{<S_2^1, w_1>, \ldots, <S_2^k,w_k>, \ldots\}, где S_2^i – строка над алфавитом A_2, в которую преобразуется строка S_1, а w_i – вес такого преобразования. Каждый переход преобразователя характеризуется двумя состояниями (между которыми осуществляется переход), входным символов (из алфавита A_1), выходным символов (из алфавита A_2) и весом перехода. Считается, что пустой символ (пустая строка) является элементом обоих алфавитов. Весом преобразования строки X в строку Y является сумма произведений весов переходов по всем путям, на которых конкатенация входных символов образует строку X, а конкатенация выходных символов образует строку Y, и которые переводят преобразователь из начального состояния в одно из терминальных.

Над WFST определяется операция композиции, на которую и опирается метод пост-обработки. Пусть заданы два преобразователя T_1 и T_2, причем T_1 преобразует строку X над A_X в строку Y над A_Y с весом w_1, а T_2 преобразует Y над A_Y в строку Z над A_Z с весом w_2. Тогда преобразователь T_1 \circ T_2, называемый композицией преобразователей, преобразует строку X в строку Z с весом w_1 \cdot w_2. Композиция преобразователей является вычислительно затратной операцией, но может вычисляться лениво – состояния и переходы результирующего преобразователя могут быть построены в момент, когда к ним необходимо совершать доступ.

Алгоритм пост-обработки результата распознавания на основе WFST опирается на три основных источника информации – модель гипотез HM, модель ошибок EM и языковую модель LM. Все три модели представляются в виде взвешенных конечных преобразователей:

  1. Модель гипотез HM представляет из себя взвешенный конечный автомат (частный случай WFST – каждая строка преобразуется сама в себя, вес преобразования совпадает с весом самой строки), принимающий гипотезы, видвинутые системой распознавания поля. К примеру, пусть результатом распознавания текстового поля является последовательность ячеек C_1, C_2, \ldots, C_N, а каждая ячейка соответствует результату распознавания некоторого символа и представляет собой множество альтернатив и их оценок (весов): C_i = \{<a_{i1}, q_{i1}>, \ldots, <a_{ik}, q_{ik}>\}, где a_{ij} – j-й символ алфавита, q_{ij} – оценка (вес) этого символа. Тогда модель гипотез можно представить в виде конечного преобразователя с (N+1)-м состоянием, уложенным в цепочку: 0-е состояние является начальным, N-е – терминальным, переходы осуществляются между (i-1)-м и i-м состояниями и соответствуют ячейке C_i. На j-м переходе входным и выходным символом является символ a_{ij}, а вес перехода соответствует оценке данной альтернативы. Ниже на рисунке представлен пример модели гипотез, сооветствующей результату распознавания строки из трех символов.

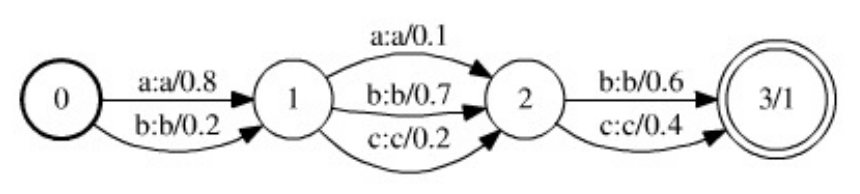
    Рис. 1. Пример модели гипотез, представленной в виде WFST (рисунок из этой статьи). Переходы с нулевым весом опущены.

  1. Модель ошибок EM является взвешенным конечным преобразователем, кодирующим всевозможные преобразования гипотез, которые можно производить для их приведения в соответствие языковой модели. В самом простом случае она может быть представлена в виде WFST с единственным состоянием (которое является и начальным и терминальным). Каждый переход кодирует некоторое изменение символа с соответствующим весом. К примеру, весом замены символа может являться оценка вероятности соответствующей ошибки алгоритма распознавания символа.
  2. Языковой моделью LM является представление синтаксиса и семантики распознаваемого поля в виде взвешенного конечного автомата. Т.е. языковой моделью яляется автомат, принимающий все допустимые значения рассматриваемого поля (и выставляющий каждому допустимому значению некоторый вес).

После определения модели гипотез, ошибок и языковой модели задача пост-обработки результатов распознавания теперь может быть поставлена следующим образом: рассмотрим композицию всех трех моделей T=HM\circ EM\circ LM (в терминах композиции WFST). Преобразователь T кодирует всевозможные преобразования строк X из модели гипотез HM в строки Z из языковой модели LM, применяя к строкам X преобразования, закодированные в модели ошибок EM. Причем вес такого преобразования включает вес исходной гипотезы, вес преобразования и вес результирующей строки (в случае взвешенной языковой модели). Соответственно в такой модели оптимальной пост-обработке результата распознавания будет соответствовать оптимальный (с точки зрения веса) путь в преобразователе T, переводящий его из начального в одно из терминальных состояний. Входная строка на этом пути будет соответствовать выбранной исходной гипотезе, а выходная строка – исправленному результату распознавания. Оптимальный путь можно искать с помощью алгоритмов поиска кратчайших путей в ориентированных графах.

Преимуществами данного подхода является его общность и гибкость. Модель ошибок, к примеру, может быть без труда расширена таким образом, чтобы учесть удаления и добавления символов (для этого всего лишь стоит добавить в модель ошибок переходы с пустым выходным или входным символом соответственно). Однако у такой модели есть и существенные недостатки. Во-первых, языковая модель здесь должна быть представлена в виде конечного взвешенного конечного преобразователя. Для сложных языков такой автомат может получиться довольно громоздким, и в случае изменения или уточнения языковой модели будет необходимо его перестроение. Также необходимо заметить, что композиция трех преобразователей в качестве результата имеет, как правило, еще более громоздкий преобразователь, а эта композиция вычисляется каждый раз при запуске пост-обработки одного результата распознавания. Ввиду громоздкости композиции, поиск оптимального пути на практике приходится выполнять эвристическими методами, такими как A*-search.

Метод на основе проверяющих грамматик


Используя модель проверяющих грамматики можно построить более простую модель задачи пост-обработки результатов распознавания, которая будет не насколько общей, как модель на основе WFST, однако легко расширяемой и простой в имплементации.

Проверяющей грамматикой будем называть пару G=<A,P>, где A – алфавит, а P – предикат допустимости строки над алфавитом A, т.е. P:A^*\rightarrow\{0,1\}. Проверяющая грамматика кодирует некоторый язык над алфавитом A следующим образом: строка S\in A^* принадлежит языку, если предикат P принимает на этой строке истинное значение. Стоит заметить, что проверяющая грамматика является более общим способом представления языковой модели, чем конечный автомат. Действительно, любой язык, представимый в виде конечного автомата T, может быть представлен в виде проверяющей грамматики (с предикатом P(S)\Leftrightarrow S\in \mathrm{acc}(T), где \mathrm{acc}(T) – множество строк, принимаемых автоматом T. Однако не все языки, которые можно представить в виде проверяющей грамматики, представимы в виде конечного автомата в общем случае (к примеру, язык слов неограниченной длины над алфавитом A=\{a,b\}, в которых количество символов a больше, чем количество символов b).

Пусть задан результат распознавания (модель гипотез) в виде последовательности ячеек C_1, C_2, \ldots, C_N (таких же, как и в предыдущем разделе). Для удобства будем считать, что каждая ячейка содержит K альтернатив и все оценки альтернатив принимают положительное значение. Оценкой (весом) строки будем считать произведение оценок каждого из символов этой строки. Если модель языка задана в виде проверяющей грамматики G=<A,P>, то задача пост-обработки может быть сформулирована в виде задачи дискретной оптимизации (максимизации) на множестве управлений A^N (множестве всех строк длины N над алфавитом A) с предикатом допустимости P и функционалом F(S)=\prod_{i=1}^{N}q_i(S_i), где q_i(S_i) – оценка символа S_i в i-й ячейке.

Любая задача дискретной оптимизации (т.е. с конечным множестве управлений) может быть решена при помощи полного перебора управлений. Описываемый алгоритм эффективно перебирает управления (строки) в порядке убывания значения функционала до того момента, пока предикат допустимости не примет истинного значения. Зададим как M максимальное количество итераций алгоритма, т.е. максимальное количество строк с максимальной оценкой, на которой будет вычисляться предикат.

Вначале проведем сортировку альтернатив по убыванию оценок, и будем далее считать что для любой ячейки C_i верно неравенство q_{ij}\ge q_{ik} при j<k. Позицией будем называть последовательность индексов j_1,\ldots,j_N, соответствующее строке a_{1j_1},\ldots,a_{Nj_N}. Оценкой позиции, т.е. значением функционала на этой позиции, считаем произведение оценок альтернатив, соответствующих индексам, входящих в позицию: \prod_{i=1}^N q_i{j_i}. Для хранения позиций потребуется структура данных PositionBase, позволяющая добавлять новые позиции (с получением их адреса), получать позицию по адресу и проверять, добавлена ли заданная позиция в базу.

В процессе перечисления позиций мы будем выбирать непросмотренную позицию с максимальной оценкой, после чего добавлять в очередь на рассмотрение PositionQueue все позиции, которые можно получить из текущей добавлением единицы к одному из индексов, входящих в позицию. Очередь на рассмотрение PositionQueue будет содержать тройки <Q,R,I>, где Q – оценка непросмотренной позиции, R – адрес просмотренной позиции в PositionBase, из которой была получена данная позиция, I – индекс элемента позиции с адресом R, который был увеличен на единицу для получения данной позиции. Для организации очереди PositionQueue потребуется структура данных, позволяющая добавлять очередную тройку <Q,R,I>, а также извлекать тройку с максимальной оценкой Q.

На первой итерации алгоритма необходимо рассмотреть позицию S_1=\{1,1,\ldots,1\}, обладающую максимальной оценкой. Если предикат P принимает на строке, соответствующей этой позиции, истинное значение, то алгоритм завершается. В противном случае позиция S_1 добавляется в PositionBase, а в PositionQueue добавляются все тройки вида <Q\cdot q_{i2}/q_{i1},R(S_1),i>, для всех i\in\{1,\ldots,N\}, где R(S_1) – адрес начальной позиции в PositionBase. На каждой последующей итерации алгоритма из PositionQueue извлекается тройка <Q,R,I> с максимальным значением оценки Q, по адресу исходной позиции R и индексу I восстанавливается рассматриваемая позиция S. Если позиция S уже добавлена в базу рассмотренных позиций PositionBase, то она пропускается и из PositionQueue извлекается очередная тройка с максимальным значением оценки Q. В противном случае на строке, соответствующей позиции S проверяется значение предиката P. Если предикат P принимает на этой строке истинное значение, то алгоритм завершается. Если предикат P не принимает истинное значение на этой строке, то строка S добавляется в PositionBase (с присвоением адреса R(S)), в очередь PositionQueue добавляются все производные позиции и происходит переход к следующей итерации.

FindSuitableString(M, N, K, P, C[1], ..., C[N]):
    для каждого i : 1 ... N:
        сортировка C[i] по убыванию оценок альтернатив
    (конец цикла)
    инициализация PositionBase и PositionQueue
    S_1 = {1, 1, 1, ..., 1}
    если P(S_1): 
        ответ: S_1, алгоритм завершается
    (конец условия)
    добавление S_1 в PositionBase с адресом R(S_1)
    для каждого i : 1 ... N:
        если K > 1, то:
            добавить тройку <Q * q[i][2] / q[i][1], R(S_1), i> в PositionQueue
        (конец условия)
    (конец цикла)
    пока количество позиций в PositionBase меньше M:
        пока не пуста PositionQueue:
            извлечь из PositionQueue тройку <Q, R, I> с максимальной Q
            S_from = позиция в PositionBase по адресу R
            S_curr = {S_from[1], S_from[2], ..., S_from[I] + 1, ..., S_from[N]}
            если S_curr содержится в PositionBase:
                продолжаем цикл
            иначе:
                добавить S_curr в PositionBase с адресом R(S_curr)
            (конец условия)
            если P(S_curr):
                ответ: S_curr, алгоритм завершается
            (конец условия)
            для каждого i : 1 ... N:
                если K > S_curr[i]:
                    добавить тройку <Q * q[i][S_curr[i] + 1] / q[i][S_curr[i]], 
                                     R(S_curr),
                                     i> в PositionQueue
                (конец условия)
            (конец цикла)
            выход из внутреннего цикла
        (конец цикла)
    (конец цикла)
    ответ не найден за M итераций


Заметим, что за M итераций будет осуществлена проверка предиката не более чем M раз, произойдет не более M добавлений в PositionBase, а добавление в PositionQueue, извлечение из PositionQueue, а также поиск в PositionBase произойдет не более M\cdot N раз. Если для реализации PositionQueue используется структура данных “куча”, а для организации PositionBase используеся структура данных “бор”, то трудоемкость алгоритма составляет O\left(M \cdot \left(p(N) +N^2+N \log(M\cdot N)\right)\right), где p(N) – трудоемость проверки предиката P на строке длины N.

Пожалуй, самым важным недостатком алгоритма на основе проверяющих грамматик является то, что он не может обрабатывать гипотезы разной длины (которые могут возникнуть из-за ошибок сегментации: потеря или возникновение лишних символов, склейки и разрезания символов и т.п.), тогда как изменения гипотез вида “удаление символа”, “добавление символа”, или даже “замена символа парой” могут быть закодированы в модели ошибок алгоритма на основе WFST.

Однако быстродействие и простота использования (при работе с новым типом поля нужно просто дать алгоритму доступ к функции валидации значения) делают метод на основе проверяющих грамматик очень мощным инструментом в арсенале разработчика систем распознавания документов. Мы используем данный подход для большого количества разнообразных полей, таких как всевозможные даты, номер банковской карты (предикат – проверка Лун-кода), поля машинно-читаемых зон документов с контрольными суммами, и многих других.


Публикация подготовлена на основе статьи: Универсальный алгоритм пост-обработки результатов распознавания на основе проверяющих грамматик. K.Б. Булатов, Д.П. Николаев, В.В. Постников. Труды ИСА РАН, Т. 65, № 4, 2015, стр. 68-73.