Рентгеновская томография - один из двух (наряду с МРТ) самых известных способов “заглянуть внутрь” непрозрачных объектов. В медицине он является инструментом клинического мониторинга и средством терапии, в индустрии помогает контролировать технологические процессы, в таможне - найти то, что кое-кто предпочел бы спрятать. Эта технология в нашей стране развивается in house на мировом уровне. Но мы в Smart Engines пишем про томографию так часто не только поэтому. Мы - ученые и изобретатели, а томография - неиссякаемый источник проблем и задач, требующих решения (мы уже писали о несовершенных детекторах и широкополосном излучении). Сегодня мы расскажем о том, что делать, если объект исследования не помещается в томограф. Вот как, например, британские ученые исследуют коня в зоопарке. Голову коня в гентри поместить удается, а с остальным дела обстоят сложнее. Пример не очень серьезный, но жизненный. Кто в лаборатории работал, тот в зоопарке не смеется. Заглянув под кат вы узнаете, как получается, что у физиков сантиметровый образец не помещается в километровый томограф, и чем тут могут помочь вычислительные математики.

Наш томографический маскот воодушевляет специалистов буквально всеми своими ммм… деталями. Вот и с общими геометрическими формами все очень удачно. Гентри ей - как хула-хуп: можно сканировать хоть сверху-вниз, хоть снизу-вверх.

Впрочем, для боди-позитивного маскота можно было бы построить гентри побольше -  в чем проблема? Но не все томографические комплексы вообще используют гентри. Есть такая машина - синхротрон. Машиной их называют специалисты, и это может вызвать неправильные образы при первом знакомстве. Размеры такой “машины” достигают километров, а строятся они, бывает, всем миром. В полном смысле этого слова. Например, синхротрон ESRF, расположенный во французском городе Гренобле, был построен в 1994 году совместными усилиями 20 стран. Синхротрон дает мощнейший узконаправленный пучок рентгеновских лучей. Такой мощный, что время многих измерений сокращается в десятки и сотни тысяч раз. Для регистрации рентгеновского излучения на его станциях используются уникальные плоскопараллельные детекторы с высочайшим пространственным разрешением. Излучатель и детектор остаются неподвижными, а образец вращается. Часто размеры исследуемых объектов, мельчайшие детали которых требуется рассмотреть, большие, а вот размеры детекторов ограничены.

Давайте посмотрим на результат измерений типичного биологического объекта в такой томографической схеме. Это фрагмент кости, отснятый с субмикронным разрешением. Измерения проведены на современном швейцарском синхротроне Swiss Light Source Paul Scherrer Institut. Намётанный глаз позволяет увидеть и контуры объекта, и трабекулы (перегородки) внутри. Но при таком разрешении объект не помещается целиком в поле зрения детектора. На каждой из проекций просматривается только часть объекта.

Похожее мы наблюдали в детстве, когда подсматривали в замочную скважину. Мы видели только часть запертой от нас комнаты. Заглядывая в нее под разными углами, можно расширить поле зрения, увидеть больше, но общую картину придется “сшивать” силой воображения. Традиционные алгоритмы томографической реконструкции для такого не предназначены.

Чтобы лучше почувствовать проблему, обратимся, как это принято среди ученых, к модели. Возьмем в качестве модельного объекта грецкий орех, совсем недавно оттомографированный в разных режимах нашими коллегами из Голландии. На картинке ниже показан орех и его рентгеновское изображение.

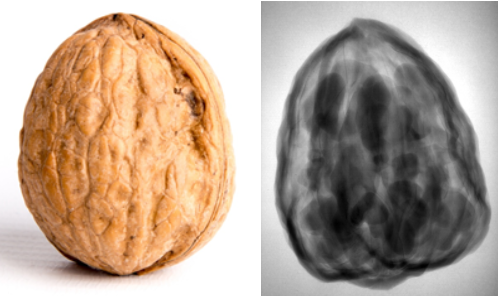
По структуре орех похож на кость, и для него нам известен ground truth - реконструкция, полученная при полных данных.

Теперь посмотрим, что мы сможем реконструировать при измерениях “через замочную скважину”. На рисунке ниже красным прямоугольником показано поле зрения нашего воображаемого детектора.

При таком соотношении размеров вместо целой синограммы объекта (что это такое, мы уже писали на Хабре) будет видна только ее часть (ниже в красной рамке).

Поскольку в детектор помещается больше половины ореха, то при вращении все его части когда-нибудь попадают в поле зрения детектора. Сама же синограмма имеет характерную структуру и кажется, что её фрагмент возможно экстраполировать до полного размера.

Будем строить такую синограмму, чтобы 1) она в области измерений совпадала с экспериментальной синограммой, 2) существовал объект, которому соответствовала бы наша синограмма (это нетривиальный факт, но не любая функция является синограммой). Предложенный нами для этого итерационный алгоритм называется Field Of View Extension Algorithm - FOVEA (любопытные хабровчане могут порыться в интернете и отгадать, почему аббревиатура составляет именно это слово).

Вот пошаговое описание алгоритма:

1. Создадим массив , заполненный . В нём мы будем итеративно обновлять значения элементов восстанавливаемого цифрового объёма.

2. Рассчитаем синограммы от .

3. Заменим рассчитанные на Шаге 2 значения доступными нам экспериментальными значениями - .

4. Проведём томографическое восстановление из синограммы методом FBP.

5. Рассчитаем синограмму от .

6. Сравним (например, рассчитав L2 норму) и в той области, где мы знаем экспериментальные значения. Если расхождение малое, т.е. экспериментальная и модельная синограммы совпадают, то конец расчёта: искомая реконструкция лежит в . В противном случае переходим на Шаг 3.

Ниже приведены результаты реконструкции обрезанной синограммы методами FBP и FOVEA.

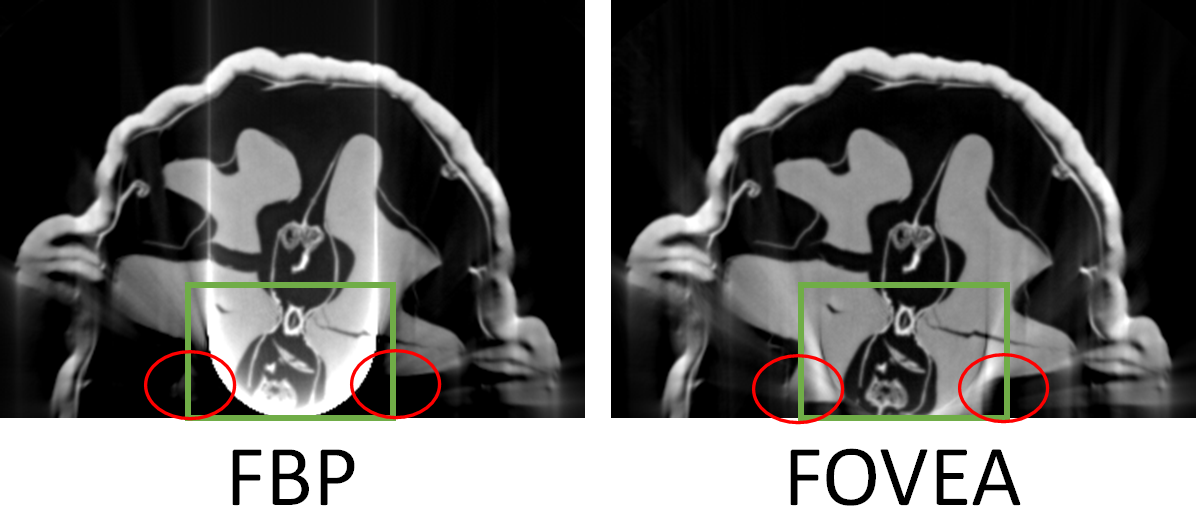
Из иллюстраций ясно, что на неполных данных мы избавились от области засветки (в зелёном прямоугольнике и “усы” вверх). Уже это позволяет увидеть больше деталей восстановленного ореха. Но, кроме того, нам удалось увидеть те части ореха, которые вообще не были видны до этого (в красных эллипсах).

Конечно, хорошо иметь полные данные и увидеть орех целиком (см рисунок ниже), но иметь алгоритм, который позволяет из испорченных данных вытянуть дополнительную информацию, тоже хорошо.

Над методами томографии высокого пространственного разрешения продолжают биться ученые всего мира. Ведь так хочется увидеть каждый нейрон в нашей голове и разгадать, наконец, как работает человеческий “нейрокомпьютер”. Для этого нужно нанометровое разрешение. 1 кубический миллиметр содержит квинтиллион вокселей размером 1 нанометр. Если значение вокселя кодируется числом с плавающей точкой одинарной точности (float32), то только для хранения результатов реконструкции потребуется 4 эксабайта (4 106 Тбайт) памяти. Но в голове ни много ни мало, а порядка 30 миллионов таких кубических миллиметров. Поэтому сегодня в высоком разрешении томографируют не весь мозг, а отдельные его участки, для чего их необходимо извлечь из головы. Что-то нам подсказывает, что методы томографирования “через замочную скважину” будут актуальными еще долго...