Вступление

В настоящее время интеллектуальные транспортные системы (англ.: Intelligent Transport Systems, ITS) активно развиваются. Их функционирование невозможно без создания телекоммуникационных систем, позволяющих транспортным средствам обмениваться информацией со внешними устройствами (англ. Vehicle-to-Everything, V2X). Транспортные средства накапливают информацию посредством различных сенсоров, радаров, лидаров и камер. Для обеспечения автономного вождения и передвижения машин в плотном строю (так называемый platooning) необходимо обеспечивать обмен этой информацией между различными транспортными средствами. Обмен информацией может также осуществляться с элементами дорожной инфраструктуры, что позволяет обеспечивать большую безопасность движения посредством передачи объектами инфраструктуры предупреждающих сообщений. Кроме того, существует большое число других приложений, которые обеспечивают удобство вождения и безопасность, а также уменьшают число пробок и предоставляют различные развлекательные сервисы. Разнообразные приложения порождают различные требования на задержки, надёжность и скорость беспроводной передачи данных. Однако кроме требований на производительность сети во многих случаях важно, чтобы передаваемые данные были защищены. В этой статье я хотел бы дать краткий обзор основных механизмов стандарта IEEE 1609.2, который описывает методы защиты информации в транспортных сетях, построенных по технологии Wi-Fi.

DSRC телекоммуникации

На данный момент одним из самых распространённых способов коммуникации в V2X является выделенная связь на короткие расстояния (англ.: Dedicated Short Range Communications, DSRC), для обеспечения которой используется набор стандартов беспроводной связи в транспортной среде: стандарты IEEE 1609 и IEEE 802.11p. Комитетом IEEE был выпущен специальный гайд, в котором они детально описаны. Заинтересовавшиеся могут найти его по ссылке.

Стандарт IEEE 802.11p описывает работу физического и основной части MAC уровня модели OSI в диапазоне частот 5,9 ГГц (и 60 ГГц опционально). Как видно, этот диапазон частот отличается от частот, на которых работает "классический Wi-Fi": 2,4 ГГц и 5 ГГц. "Классические" частоты являются нелицензируемыми, и это приводит к их зашумлённости передачами устройств, работающих по другим стандартам, что крайне нежелательно для транспортных сетей, которые сделаны в частности для поддержки приложений, обеспечивающих безопасность дорожного движения. В свою очередь, диапазон частот в 5,9 ГГц является бесплатным и лицензированным в том плане, что в этом диапазоне могут работать только устройства, использующие определённый набор стандартов. Стандарт IEEE 1609.4 описывает многоканальные методы доступа к среде, которые позволяют поочерёдно передавать сразу в двух каналах, например, канале для передачи данных и канале для контрольных сообщений. IEEE 1609.3 описывает WSMP (Wave Short Message Protocol), который является альтернативой протоколам TCP/UDP и IP на транспортном и сетевом уровне соответственно. Также стандарт IEEE 1609.3 выполняет некоторые другие функции, например, выбор канала для передачи данных. Стандарт IEEE 1609.2 описывает методы обеспечения безопасной передачи данных и именно ему я хотел бы уделить внимание в данной статье.

Основные положения IEEE 1609.2

Стандарт IEEE 1609.2 основывается на асимметричной криптографии и в частности описывает методы шифрования сообщений и методы создания цифровой подписи. Единицей данных для этого стандарта является так называемый SPDU (Secured Protocol Data Unit), который состоит из защищаемых данных и специальных полей для обеспечения защиты информации. IEEE 1609.2 защищает только данные, являющиеся полезной нагрузкой для протокола транспортного уровня. То есть заголовки транспортного, сетевого, LLC, MAC, а тем более физического уровней стандарт IEEE 1609.2 не защищает. Пример пакета, который иллюстрирует местоположение защищаемых данных, представлен на рисунке ниже. Базовая структура SPDU стандарта IEEE 1609.2 представлена здесь под буквой D:

Так как трафик в транспортных сетях по большей части является широковещательным, описывать методы шифрования я не буду, так как при шифровании у принимающего устройства есть секретный ключ, известный только ему, а у передающих открытый - расшифровать сообщений может только принимающее устройство, то есть передача должна быть не широковещательной, а по конкретному адресу. Поэтому я сосредоточусь на описании инфраструктуры для криптографии с открытым ключом (англ.: PKI, Public Key Infrastructure) применительно к транспортным сетям и на алгоритме создания и проверки цифровой подписи. Цифровая подпись используется для проверки того, что отправитель сообщения действительно является тем устройством, за которое себя выдаёт, и для проверки того, что данные не были изменены сторонним устройством. Для создания цифровой подписи устройство использует свой секретный ключ и добавляет значение цифровой подписи в специальные поля SPDU. Проверить сообщение на подлинность может любое устройство, которое знает открытый ключ, соответствующий секретному ключу передающего устройства. Так как для проверки цифровой подписи необходимо знать только открытый ключ, то добавлять цифровую подпись можно даже к широковещательным сообщениям, например, к базовым сообщениям приложений безопасности (англ.: Basic Safety Messages, BSM) и к beacon-ам (специальные кадры технологии Wi-Fi, применяемые для обмена служебной информацией). О том как устройства узнают открытый ключ, соответствующий секретному ключу, я расскажу в следующей главе.

Инфраструктура открытых ключей в сетях V2X

Сразу оговорюсь, что далее я буду говорить только о транспортных средствах, поддерживающих процедуру создания и проверки электронной подписи по стандарту IEEE 1609.2, так как на данный момент этот стандарт поддерживают не все транспортные средства. Сперва я хотел бы отметить, что у каждого транспортного средства имеется 2 типа секретных ключей: долгосрочный и краткосрочный. При этом краткосрочных ключей может быть несколько. Долгосрочный секретный ключ выдаётся при производстве транспортного средства по договорённости производителя и властей того региона, где ключ выдавался. Выдаётся он вместе с соответствующим открытым ключом, некоторой технической и идентификационной информацией о транспортном средстве и сертификатом открытого ключа (сертификат содержит открытый ключ и некоторую информацию о владельце соответствующего секретного ключа). Долгосрочный секретный ключ известен только устройству, которому он выдан, и хранится в так называемом аппаратном защитном модуле транспортного средства, из которого секретный ключ не так-то просто достать. Открытый ключ, его сертификат и некоторая идентификационная информация устройства хранятся в сертификационном центре (англ.: Certification Authority, CA), из которого другие устройства могут получить информацию о сертификате и открытом ключе зарегистрированного устройства. Стоит отметить, что во время производства нового транспортного средства оно получает также 2 открытых ключа сертификационного центра: один для проверки электронной подписи сообщений, переданных от CA, а второй на случай, если злоумышленнику удастся узнать первый секретный ключ CA. Если злоумышленнику удастся узнать этот ключ, то CA сможет сменить секретный и открытый ключ, разослав новый открытый ключ всем устройствам и подписав сообщение вторым секретным ключом. Стоит отметить, что время жизни долгосрочного секретного ключа должно быть равно времени жизни транспортного средства или по крайней мере составлять большую часть его жизни.

Теперь я хотел бы пояснить, зачем нужны краткосрочные закрытые ключи. Как я уже говорил, долгосрочный ключ рассчитан на длительное использование, поэтому хотелось бы использовать его нечасто, чтобы у злоумышленника было меньше шансов взломать этот ключ. Для этого используются секретные краткосрочные ключи. Транспортное средство генерирует несколько пар краткосрочных секретных и открытых ключей и отправляет CA сообщение с сертификатами открытых ключей. Сообщение подписывается долгосрочным закрытым ключом. После того как CA получил сертификаты краткосрочных открытых ключей от транспортного средства, он сохраняет их у себя в памяти, и далее эти сертификаты могут получить другие устройства. После отправки сертификатов краткосрочных открытых ключей CA наше устройство начинает подписывать сообщения краткосрочными секретными ключами. Периодически оно меняет свои секретные и соответствующие им открытые ключи. При этом уже использованные закрытые и соответствующие им открытые ключи стираются из памяти и больше не используются. Поэтому устройству периодически нужно генерировать новые пары открытых и закрытых ключей и рассылать соответствующие сертификаты открытых ключей на CA.

Я довольно много говорил об обмене информацией между CA и нашим устройством, но не сказал, как он осуществляется. Для пояснения я приведу следующую картинку:

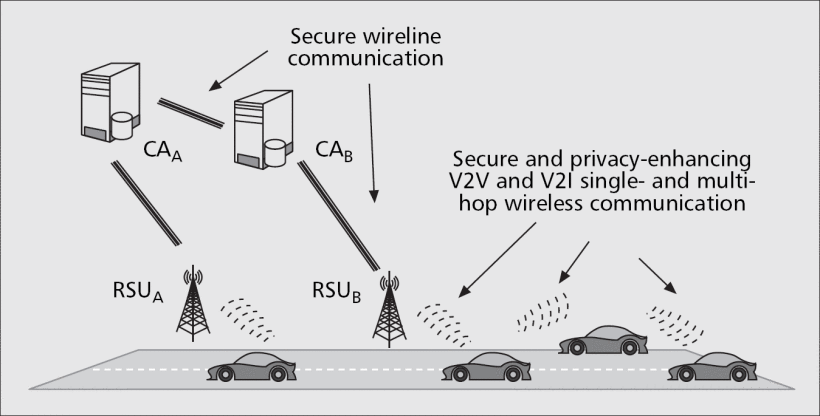
Транспортные средства обмениваются информацией с CA посредством придорожной инфраструктуры (англ.: Road-Side Unit, RSU). Ранее я писал, что стандарт IEEE 1609.2 защищает только полезную нагрузку транспортного уровня, но не заголовки транспортного уровня и нижележащих уровней модели OSI, что позволяет RSU и другим устройствам, выполняющим роль маршрутизатора, передавать сообщения от транспортного средства к CA и обратно, даже не имея возможности узнать содержимое сообщения (если оно зашифровано, например). То есть обмен информацией между автомобилями и CA осуществляется через RSU.

Теперь я хотел бы описать обмен информацией между транспортными средствами. При отправке радиомодулем автомобиля широковещательного сообщения сущность, отвечающая за безопасность передачи данных, должна прицепить к сообщению электронную подпись и сертификат открытого ключа для проверки этой электронной подписи. При приёме сообщения другое транспортное средство должно сперва проверить, что полученный сертификат зарегистрирован и отмечен как действительный в CA, а затем использовать открытый ключ из сертификата для проверки электронной подписи. Для проверки действительности сертификата при первом его получении нужно направлять запрос в CA. Дальнейшая проверка действительности сертификата может осуществляться посредством его временного сохранения в буфере транспортного средства (то есть устройство на время запоминает, что сертификат действительный).

Стоит отдельно отметить, что CA может не только регистрировать сертификаты, но и отзывать их по истечении срока жизни или по каким-то иным причинам. Так что если злоумышленник захочет сбить систему дорожной безопасности транспортного средства с толку, но сертификат открытого ключа злоумышленника не будет зарегистрирован в CA, то у него ничего не выйдет. Больше информации об инфраструктуре открытых ключей в транспортных сетях можно узнать, например, из статьи №1 или статьи №2, на которых основывается мой рассказ про инфрастурктуру открытых ключей в V2X.

Параметры алгоритма создания электронной подписи и операции на эллиптических кривых

Для создания и проверки электронной подписи в стандарте IEEE 1609.2 используется алгоритм цифровой подписи на основе эллиптических кривых (англ.: Elliptic Curve Digital Signature Algorithm, ECDSA). Здесь я дам его краткое описание. Больше информации об этом алгоритме и криптографии на эллиптических кривых можно найти, например, в этой статье на хабре или в этой научной статье. Алгоритм ECDSA позволяет создать электронную подпись сообщения с помощью закрытого ключа, а затем проверить её с помощью открытого. То есть отправитель должен знать секретный ключ, а все принимающие устройства должны знать открытый ключ. Однако кроме знания одного из двух ключей устройства также должны знать параметры алгоритма. Первыми двумя параметрами алгоритма являются коэффициенты используемой эллиптической кривой. В алгоритме ECDSA используются эллиптические кривые форме Вейерштрасса, под которыми в криптографии подразумевается множество точек (x, y) следующего вида (далее под эллиптической кривой буду подразумевать именно это множество точек):

Здесь - это поле Галуа, состоящее из целых чисел от 0 до p - 1, где p - простое число, либо степень простого числа. В криптографии p выбирают либо простым числом, либо степенью двойки. Числа a и b, являющиеся параметрами эллиптической кривой, также принадлежат . Дополнительное условие на эти коэффициенты делает эллиптическую кривую применимой в криптографии. Под "0" подразумевается нулевой элемент эллиптической кривой, при прибавлении которого к любому элементу получится тот же самый элемент. Геометрически нулевой элемент - это бесконечно удалённая точка расширенной действительной плоскости. Стоит отметить, что эллиптическая кривая имеет конечное число элементов и при правильном введении операции сложения и взятия обратного элемента становится абелевой группой относительно этой операции сложения. Чтобы геометрически пояснить операцию сложения и взятия обратного элемента, я вставлю сюда картинку, которая иллюстрирует вид эллиптической кривой в , то есть кривой вида:

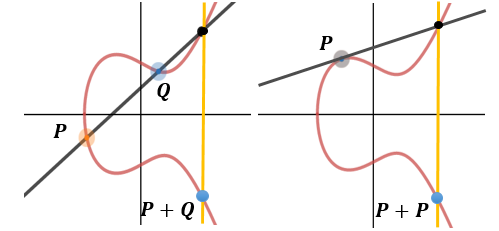
Красная кривая - это качественный вид эллиптической кривой, задаваемой уравнением выше. У такой кривой есть ось симметрии, которая в данном случае проходит через ось абсцисс. Ось симметрии позволяет ввести понятие обратного элемента: точка P эллиптической кривой называется обратной к точке M эллиптической кривой, если точка M симметрична точке P относительно оси симметрии нашей эллиптической кривой. Результат сложения симметричных точек M и P определяется следующим образом:

Стоит отметить, что на представленном выше рисунке изображена не только сама эллиптическая кривая, но и геометрический смысл операции сложения. Чтобы найти сумму двух разных точек эллиптической кривой, не симметричных относительно оси симметрии этой кривой (на рисунке точки P и Q), необходимо провести через них прямую и найти её точку пересечения с кривой (точка пересечения существует в силу условий на параметры a и b). Тогда суммой точек эллиптической кривой называется точка, обратная к указанной выше точке пересечения. Для нахождения результата сложения некоторой точки эллиптической кривой с самой собой (на рисунке P + P) необходимо провести касательную к этой точке, найти пересечение касательной с эллиптической кривой (пересечения опять-таки существует в силу условий на a и b) и взять точку, обратную к пересечению. Для реализации алгоритма ECDSA на компьютере указанные выше операции сложения необходимо записать в аналитическом виде. Это можно сделать, используя методы аналитической геометрии. Здесь я напишу лишь конечные формулы для сложения точек в полях Галуа. Будьте внимательны! Я не зря выделил последнюю фразу жирным шрифтом. Под делением в полях Галуа я подразумеваю взятие обратного элемента: элемент x поля Галуа называется обратным к элементу y поля Галуа если:

Для вычисления обратного элемента обычно используется расширенный алгоритм Евклида. С учётом замечания про взятие обратного элемента формула для сложения разных точек и , не симметричных относительно оси симметрии эллиптической кривой, имеет следующий вид (все!!! операции по модулю p):

В свою очередь, формула для сложения точки с самой собой имеет вид:

Однако a, b и p - это не единственные параметры алгоритма ECDSA. Дело в том, что алгоритм ECDSA работает не на всей эллиптической кривой, а на её циклической подгруппе, образуемой некоторой генерирующей точкой G эллиптической кривой. Все элементы этой подгруппы получаются путём сложения точки G с самой собой некоторое число раз. Порядок этой подгруппы (то есть число элементов в ней) является пятым параметром алгоритма ECDSA. По-другому порядок подгруппы можно определить как наименьшее положительное целое число n такое, что: nG = "0". Последним параметром является так называемый кофактор подгруппы. Он определяется следующим образом:

Здесь под N подразумевается порядок всей эллиптической кривой, то есть число элементов в ней. В силу так называемой теоремы Лагранжа, n всегда является делителем числа N, так что кофактор определён корректно.

В стандарте IEEE 1609.2 возможно использование лишь определённого набора параметров, для которых нет общеизвестных методов быстрого взлома алгоритма ECDSA (о том, как его можно взломать я расскажу чуть позже). Используемый набор параметров для передающего устройства можно получить вместе с его открытым ключом от CA. Примеры этих наборов можно найти, например, в этой статье в разделе ECDSA.

Алгоритм ECDSA

Теперь перейду к описанию самого алгоритма ECDSA. Этот алгоритм работает не с самим передаваемым сообщением, а с его хэшем. Хэш-функция позволяет преобразовать сообщение произвольной длины в последовательность бит фиксированной длины. При этом данное преобразование выполняется таким образом, что восстановление всех возможных исходных значений сообщения по заданному значению хэша является вычислительно сложной задачей, тогда как вычисление самой хэш-функции можно произвести быстро. Полученную после действия хэш-функции последовательность бит можно интерпретировать как десятичное число в двоичной форме записи. Именно это число используется алгоритмом ECDSA. Если это число получается большим, чем n, то хэш сообщения необходимо урезать. Стандарт IEEE 1609.2 определяет всего 2 допустимые хэш-функции: SHA-256 и SHA-384.

Теперь перейду к описанию процедуры генерации открытого и закрытого ключей. Закрытый ключ d является случайно выбранным элементом поля Галуа, лежащим в интервале [1, n - 1]. Открытый ключ вычисляется из закрытого по следующей формуле (здесь и далее набор параметров алгоритма (p, a, b, G, n, h)):

Для вычисления значения открытого ключа по закрытому ключу и генерирующей точке существуют эффективные алгоритмы, позволяющие вычислить открытый ключ быстро. А вот обратная задача, то есть вычисление закрытого ключа по известной генерирующей точке и открытому ключу, считается сложной. Эта задача называется задачей дискретного логарифмирования, и именно на сложности её решения базируется криптографическая стойкость алгоритма ECDSA. Для того чтобы эта задача была по-настоящему сложной и не решалась за приемлемое время на обычных компьютерах, необходимо выбирать большие значения p и n. Например, для одного из специфицируемых стандартом IEEE 1609.2 набора параметров алгоритма ECDSA под названием NIST P-224 параметры p и n имеют следующие значения:

Теперь перейду к процедуре генерации электронной подписи алгоритмом ECDSA. Выпишу её в виде алгоритма (m - это исходное сообщение):

1) - Сперва необходимо выбрать случайное число:

2) - Далее вычисляем точку и число:

3) - Если r = 0, то возвращаемся к шагу №1

4) - Затем необходимо вычислить значение:

5) - Если s = 0, то возвращаемся к шагу №1

6) - Возвращаем сообщение m и пару чисел (r, s)

Процедура проверки электронной подписи выглядит следующим образом:

1) - Проверяем, что:

2) - Вычисляем значения:

3) - Вычисляем точку:

4) - Подпись действительна тогда и только тогда когда:

Проверка корректности алгоритма

Теперь проверим корректность этого алгоритма (нестрого). Сперва перепишем P в несколько другом виде, учитывая что :

Учитывая определение и , получим:

Ранее было дано следующее определение:

Умножив обе части уравнения на k и поделив на s, мы получим, что:

А это значит, что:

Из написанной выше проверки корректности следует, что посредством этого алгоритма значение r было вычислено двумя способами: на передающем устройстве с помощью закрытого ключа и на принимающем с помощью открытого. Затем 2 значения r были сопоставлены друг с другом.

Заключение

В данной статье были рассмотрены базовые принципы функционирования стандарта IEEE 1609.2, описывающего защиту информации в транспортных сетях, работающих по технологии Wi-Fi. Сперва был рассмотрен набор стандартов для беспроводной связи в транспортных сетях. Затем был сделан обзор методов распределения открытых и генерации секретных ключей в сетях V2X. Далее была описана арифметика криптографии на эллиптических кривых и алгоритм ECDSA, используемый для создания электронной подписи в стандарте IEEE 1609.2. В конце была проверена корректность алгоритма ECDSA.