Здесь поговорим о вре?менных данных, служащих для информационного обмена между отдельными вычислителями в (максимально близкорасположенных) параллельных вычислительных системах.

В публикации на Habr’е “Есть ли параллелизм в произвольном алгоритме и как его использовать лучшим образом” от 26.11.2020 г. (https://habr.com/ru/post/530078/) описан исследовательский программный комплекс для анализа произвольного алгоритма на наличие скрытого потенциала параллелизма и инструментарий для построения рационального каркаса расписания параллельной программы.

Комплекс включает модуль  программного симулятора универсального вычислителя, реализующий Data-Flow (далее D-F) подход к управлению последовательностью вычислений [1] с использованием архитектуры SMP (Symmetric MultiProcessing, симметричная мультипроцессорность), позволяющий выполнять произвольную программу, разработанную на языке программирования уровня Ассемблера [2],  причем порядок операндов соответствует стилю AT&T. Программная модель использует трёхадресные команды, условность выполнения осуществляется предикатным методом, [3]). D-F симулятор позволяет гибко управлять параметрами потокового выполнения программ в соответствии с концепцией ILP (Instruction-Level Parallelism,  параллелизм  уровня машинных команд)  и автоматически (в физической реализации – на аппаратном уровне) генерировать план выполнения параллельной программы [4].

В вычислителях потоковой архитектуры процесс выбора операторов для исполнения удобно представить результатом взаимодействия некоторых сущностей, асинхронно выполняющих определенные  действия – “актёров” [5], при этом естественным образом моделируются связанные с характеристиками времени параметры обработки операторов.

Второй модуль комплекса (SPF@home, далее SPF) служит для выявления в Информационном Графе Алгоритма (далее ИГА) скрытого параллелизма методом построения Ярусно-параллельной Формы (далее ЯПФ) алгоритма [5]  c последующей реорганизацией ЯПФ путём последовательных целенаправленных изменений без нарушения информационных связей [6] для составления рационального каркаса расписания выполнения параллельной  программы. Одной из важных целей реорганизации ЯПФ является повышение плотности кода (формально определяемой в данном случае равномерностью заполнения ярусов ЯПФ операторами).  Т.к. задачи составления расписаний относят к классу NP-полных [7], в данной работе использован метод разработки, основанный на создании и итерационном улучшении  основанных на эвристическом подходе  сценариев реорганизации ЯПФ [8] (собственно сценарии разрабатываются с использованием скриптового языка Lua [9]). 

Исходными данными для модуля SPF служат ИГА-файлы стандартного формата, которые могут быть получены путём импорта из системы D-F или любым иным (в общем случае уровень операторов может быть любым – необязательно соответствующим концепции ILP).

Исходя из сложности алгоритмов обработки данную область исследований можно обоснованно отнести к наиболее сложным областям “Науки о данных” (Data Science).  

Все вышеописанные программные модули полностью Open Source, свободная вы?грузка инсталляционных файлов доступна с ресурсов http://vbakanov.ru/dataflow/content/install_df.exe и http://vbakanov.ru/spf@home/content/install_spf.exe соответственно (дополнительная информация - http://vbakanov.ru/dataflow/dataflow.htm  и http://vbakanov.ru/spf@home/spf@home.htm).

Используя в качестве инструмента указанные программные средства,  можно выявить потенциал параллелизма в заданном алгоритме и определить (предпочтительное по мнению разработчика) расписание  его исполнение на параллельной многопроцессорной системе (гомогенной или гетерогенной). С другой стороны, имеется возможность определить рациональную конфигурацию параллельного вычислителя для выполнения заданного алгоритма (класса алгоритмов). Решение последней задачи требует (кроме указания  числа и типов отдельных вычислителей)  определения параметров устройств временного хранения локальных данных, требующихся для передачи между отдельными вычислителями в процессе переработки информации.

Целевыми потребителями исследовательского программного комплекса являются разработчики компиляторов, исследователи свойств алгоритмов (в первую очередь в направлении нахождения и использования потенциала скрытого параллелизма) и преподаватели соответствующих дисциплин.

Современный вычислитель не может эффективно работать без сверхбыстродействующих устройств временного хранения  данных, разделяемых между отдельными параллельными вычислителями -  кэша и/или регистров общего назначения (оперативная память для этих целей малоприменима вследствие своей медлительности). Эти устройства являются  дорогостоящими  и поэтому оптимизация расписания выполнения алгоритма должна проводиться и по условию минимизации размеров этой памяти.

Интересно, что даже при полностью последовательном выполнении алгоритма имеется возможность оптимизировать последовательность выполнения отдельных операторов с целью минимизации размера временных данных (это может быть важно, например, для программируемых контроллеров и специализированных управляющих компьютеров). Как и в предыдущих случаях, приведенные данные верны не только для однозадачного режима выполнения программ, но и применимы для многозадачности с перегрузкой контекстов процессов при многозадачности.

Набор API-вызовов системы SPF позволяет получить информацию о требуемых при выполнении заданного алгоритма параметрах (времени жизни данных, далее ВЖД). Эти данные появляются следствием выполнения отдельных операторов и, в свою очередь, служат входными операндами для иных операторов (метафорически можно сказать, это такие ВЖД “живут между ярусами ЯПФ”).

Система SPF формально выдаёт информацию о временных данных в форме некоторых обобщённых величин, реальный размер данных должен быть  определён в med-файлах. Информация о временных данных может быть выдана в известном формате текстового файла для анализа внешней программой.

На рис.1 и 2 показаны расписания выполнения в форме ЯПФ (причём, как и было принято ранее, выполнение осуществляется в направлении увеличения номеров ярусов) алгоритма решения полного квадратного уравнения в вещественных числах (аналогично рис. 2 предыдущей статьи для исходной и модифицированной ЯПФ соответственно; при этом номера операторов в овалах (111-116) соответствуют операциям присвоения (или передачи из внешних модулей)  начальных   значений для расчёта. Диаграммы ВЖД приведены  в форме отдельных блоков, включающих  циклы “генерация – использование – уничтожение” данных, поэтому некоторые номера операторов дублируются.

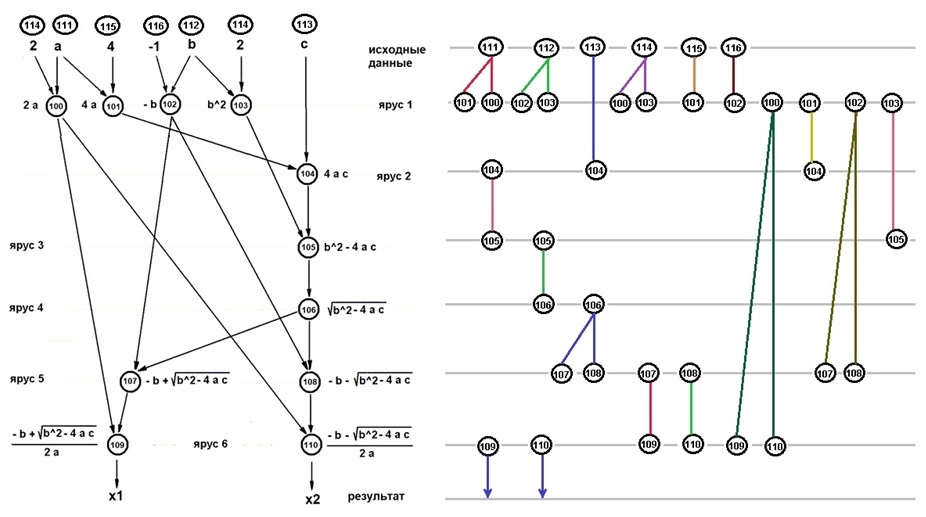
Рисунок 1 Исходная ЯПФ алгоритма (слева) и соответствующая диаграмма ВЖД (справа, формула одновременно существующих данных “6-5-4-3-3-3-2”)

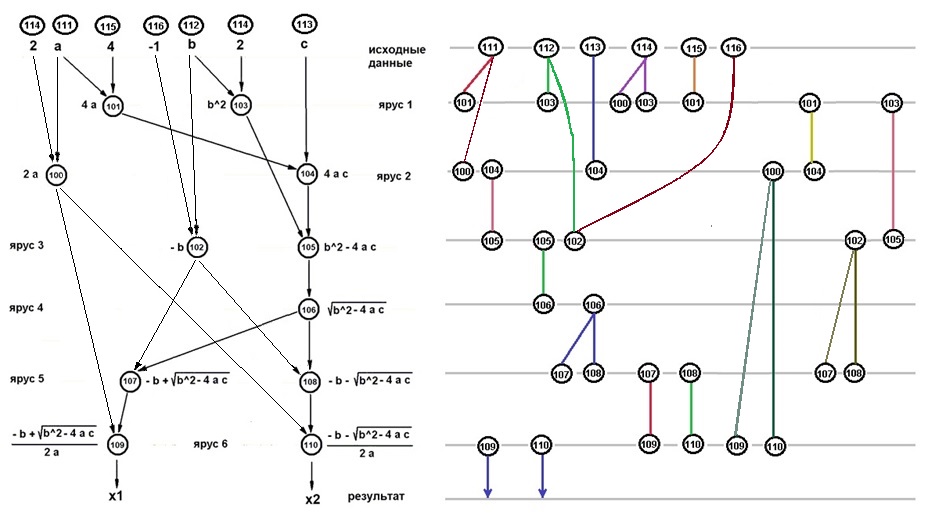
Рисунок 2 Модифицированная (один из вариантов) ЯПФ рис.1 и соответствующая ВЖД данных (формула “6-7-5-3-3-3-2”)

Из сравнения рис. 1 и 2 видим, что полезная модификация ЯПФ (позволяющая выполнить программу на двух параллельных вычислителях вместо 4-х и, соответственно, существенно повысить плотность кода) требует бо?льшей нагрузки на разделяемую память (“формула” показывает список количества обобщённых данных, существующих между ярусами  последовательно вдоль ЯПФ).

С помощью соответствующего Lua-скрипта в системе SPF показанная на рис. 1 ЯПФ была “уж?ата” до единичной ширины (фактически метод “обратного инжиниринга”); получены несколько планов выполнения программы (рис. 3), эквивалентных исходному ИГА по информационным связям. Реконфигурируемая т.о. ЯПФ  вырождена и содержит 11 последовательно исполняемых операторов (плюс уровни  исходных и выходных данных).

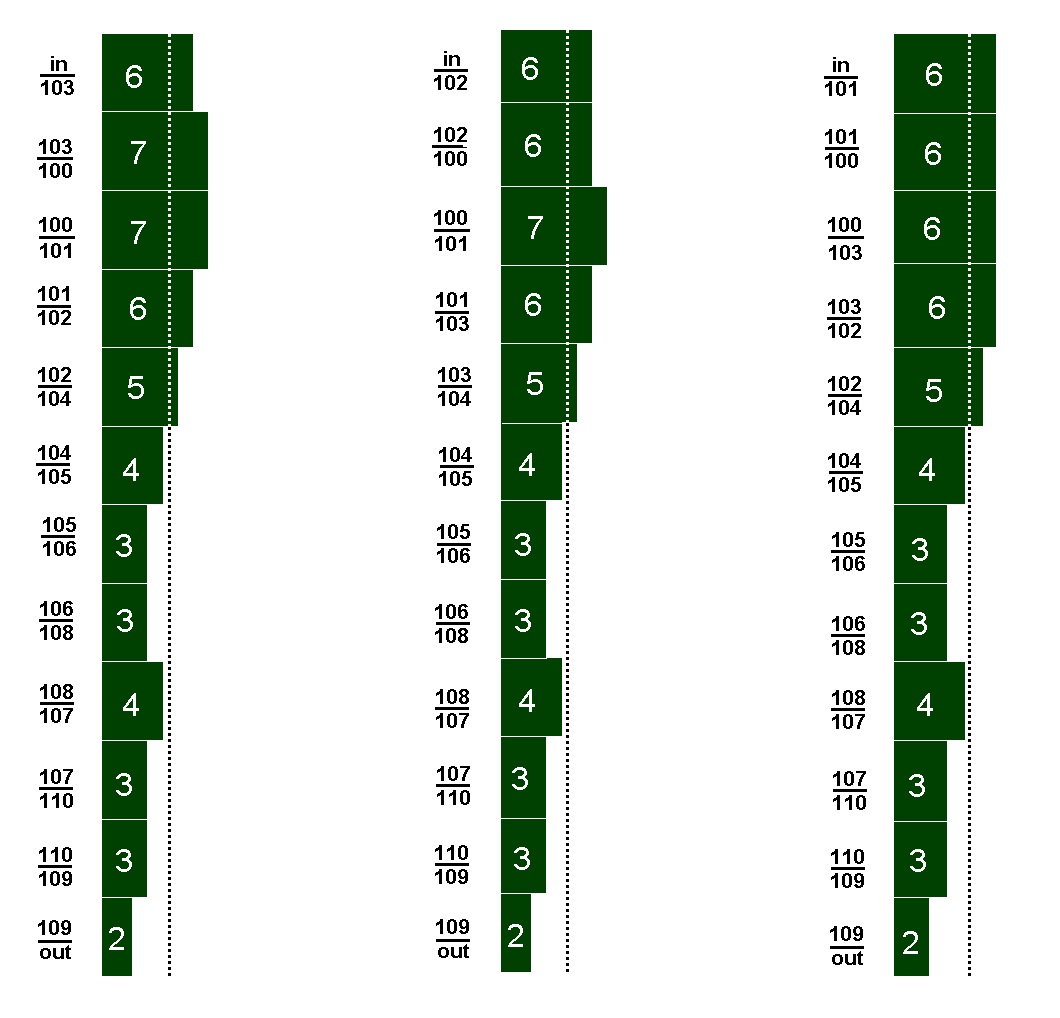
Рисунок 3 Количество одновременно  существующих данных для трёх (слева направо) вариантов последовательного выполнения алгоритма рис. 1  (слева от диаграммы – промежуток ярусов с указанием номеров операторов в формате “предыдущий / последующий”; in и out – входные и выходные данные соответственно, в прямоугольниках диаграммы – количество данных)

Первыми (не единственными!) претендентами на линейность исполнения являются находящиеся на ярусах 1,5,6 (рис. 1) операторы, причем вследствие  ортогональности по данным они могут быть выполнены в любой  последовательности. При этом достигаются разные качества распределения ВЖЛД (на рис. 3 варианта,  локальным оптимумом из которых является последний, характеризующийся максимумом числа данных 6 единиц). В данном случае вычислительная сложность процедуры реорганизации ЯПФ явилась незначительной - оказалось достаточным всего двух перестановок операторов (изменения в положении коснулись операторов 101,102,103.  Даже в таком простом примере  результат оптимизации “стоит свеч”, для более сложных случаев качество оптимизации будет более значительным.

Cледующей  задачей является распределение регистров разделяемой памяти, эта задача может быть решена известным приемом  дискретной математики – методом раскра?ски графа [10].

Т.о. исследования показывают, что не только в случае параллельного,  но и последовательного выполнения программ вполне возможна оптимизация  вычислительных систем в направлении минимизации ресурсов устройств временного хранения данных  путем реализации разумного плана выполнения отдельных операций.

Список литературы

1.  J.B.Dennis, D.P.Misunas. A Preliminary Architecture for a Basic Data-Flow Processor. In Proc. Second Annual Symp. Computer Architecture, pр. 126-132, Houston, Texas, January, 1975.

2.  Баканов В.М. Параллелизация обработки данных на вычислителях потоковой (Data-Flow) архитектуры.  // Журнал “Суперкомпьютеры”, — M.: 2011, № 5, с. 54-58.

3.  Э.Таненбаум, Т.Остин. Архитектура компьютера. — СПб.:  Изд. Питер,   2019. — 816 c.

4.  Баканов В.М. Управление динамикой вычислений  в процессорах потоковой архитектуры  для различных типов алгоритмов. // Журнал “Программная инженерия", — М.: 2015, № 9, c. 20-24.

5.  Федотов И.Е. Параллельное программирование. Модели и приёмы. — М.: СОЛОН-Пресс, 2018. — 390 с.

6.  Баканов В.М. Программный комплекс для  разработки методов построения оптимального каркаса параллельных программ. // Журнал “Программная инженерия", — М.: 2017, том 8, № 2, c. 58-65.

7.  M.R.Gary, D.S.Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H.Freeman and Company, San Francisco, 1979. — 338 pp.

8.  V.M.Bakanov.  Software complex for modeling and optimization of program implementation on parallel calculation systems. Open Computer Science, Volume 8, Issue 1, Pages 228–234, ISSN (Online) 2299-1093, DOI: https://doi.org/10.1515/comp-2018-0019.

9.  Roberto Ierusalimschy. Programming in Lua. Third Edition.  PUC-Rio, Brasil, Rio de Janeiro, 2013. — 348 p.

10. Карпов В.Э. Теория компиляторов. Часть 2. Двоичная трансляция. URL: http://www.rema44.ru/resurs/study/compiler2/Compiler2.pdf (дата обращения 15.12.2020).