В публикации https://habr.com/ru/post/530078/ я рассказывал  о возможностях пото?кового (архитектуры Data-Flow, далее DF) параллельного вычислителя. Особенности выполнения программ на нём столь необычны и интересны, что о них следует сказать “два слова”. Эксперименты проводились на компьютерном симуляторе DF-машины, входящем в исследовательский комплекс для выявления параллелизма в произвольном алгоритме и выработке рационального расписания  выполнения этого алгоритма на гомогенном или гетерогенном поле параллельных вычислителей (та же публикация).

Вычислительная модель DF уже оказала положительное влияние на развитие теории и практики программирования, и в перспективе её использование также может оказаться весьма полезным. Думаю, этого вполне достаточно для проведения исследований указанной  пост-неймановской архитектуры, которые  могут выявить пути дальнейшего развития вычислительных практик и с этой точки зрения полезны.

Основной признак DF – выполнение операторов не в заданном (например, сгенерированным компилятором на основе исходного текста) порядке, а по условию “готовности их к выполнению” (далее ГКВ). В DF-машине приказ выполнить определённую команду заменён на разрешение её выполнить (причём исполнение “как можно раньше” совсем необязательно).  Условие ГКВ оператора (а понимаемый в расширенном смысле “оператор” может иметь размер гранулы  от машинной инструкции до блока любой величины, однако между гранулами требуется ортогональность по данным – условие параллельного выполнения) является “готовность”  всех его операндов (им должны быть присвоены значения как результат выполнения иных операторов – включая простое присваивание); сказанное соответствует гранулярности от уровня машинных команд до значительно больших значений.

Реализация сказанного может быть как  аппаратной, так  и программной (но последнее чревато снижением быстродействия). В настоящее время применение идеологемы ILP (Instruction-Level Parallelism,  параллелизм  уровня команд) встречает трудности при реализации (обработка  “по машинной команде зараз” сопряжён с излишними накладными расходами), существуют надежды на прорыв при использовании памяти с  ассоциативным доступом в качестве общей). Сейчас более перспективным считается основанный на  “гибридных” моделях подход, при этом DF-принцип чаще применяется к потокам выполнения (“нити”, threads,  разделяющие код и контекст данного процесса); именно они здесь выступают в качестве гранул параллелизма. Проблемой в этом случае является декомпозиция исходной программы на гранулы повышенного размера (разбиение на машинные команды абсолютно естественно и вопросов обычно не вызывает).

Началом истории развития DF-архитектуры вычислителей принято считать работы Джека Денниса и его коллег из MIT второй половины 70-х г.г. (личное отношение автора к данному подходу представлено здесь). Имеются данные о более раннем использовании принципа “внеочерёдного исполнения” (out-of-order execution) машинных инструкций (здесь “внеочерёдной” фактически соответствует ГКВ-условию) в машинах CDC 6600 (Control Data Corp.) и IBM System/360 Mod. 91 (IBM Corp.).

Самая простая DF-машина – со статической архитектурой (каждый  физический АИУ (Арифметическое или Арифметико-логическое Исполнительное Устройство – будем в соответствии с предложенной академиком В.С.Бурцевым терминологией так называть отдельные параллельно работающие вычислительные устройства) однозначно связан с его логическим экземпляром, динамическая архитектура позволяет скрыть недостатки статической и существенно расширить возможности собственно DF-подхода.

Для исследовательских моделей таких систем разработаны языки программирования со значительными возможностями (в некоторых случаях допускается даже рекурсия!). Однако  автор публикации не ставил планов по созданию или использованию языков программирования и (в соответствие с поставленными целями) остановился на низкоуровневых командах (синтаксис  описан в работе https://habr.com/ru/post/535926/).

Укрупнённая схема используемого симулятора  DF-вычислителя приведена на рис. ниже. В целом устройство представляет собой кольцевую структуру, включающую АИУ (физически могущие быть представленными отдельными процессорами или микропроцессорными ядрами), общую оперативную память, буферную память команд и два коммутатора  (выходной для замены значений операндов значениями результата вычислений после АИУ и выходной для распределения ГКВ-операторов между полем параллельных АИУ). Задание приоритета выбора ГКВ-операций из буфера команд позволяет в определённых пределах управлять динамикой выполнения программ. Команды выполняются асинхронно – различные этапы обработки данных на одном АИУ в общем случае никак  не связаны с этапами обработки на других  АИУ (вообще обычно поле АИУ предполагается гетерогенным).

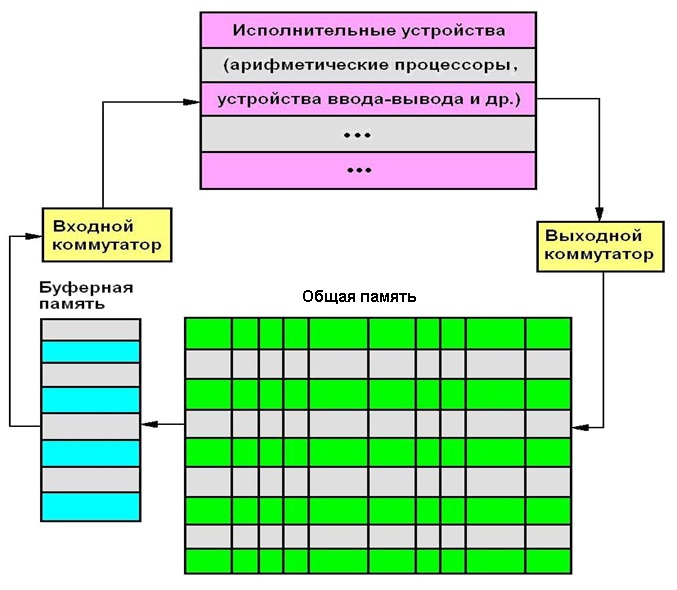
На рис. символически показана наиболее простейшая  организация общей памяти  (фактически классическая “база данных в оперативной памяти”, при этом коды каждого оператора располагаются в оперативной памяти линейно с определённым смещением). Поиск ГКВ-операторов в такой памяти может быть организован последовательным перебором (катастрофически медленно при реальных объёмах памяти!) или с использованием известных приёмов (хеширование etc). Именно поэтому считается, что применение ассоциативной памяти (аппаратный поиск методом одновременного сравнения “по образцу” со всеми ячейками памяти) позволит избавиться от многих “слабых мест” при реализации полномасштабных DF-вычислителей

Итак, изъясняясь в стиле профессора Выбегалло  - “Le vin est tire, il faut le boire!"... Лучший способ узнать, “что у её внутре” (словами бессмертного “старикашки Эдельвейса”) – заставить объект работать. DF-вычислитель легко “вскрывает” скрытые особенности алгоритмов в области параллелизма. Это очень импонирует автору, полагающему именно алгоритм  фундаментом всей “машинерии” преобразований данных (сиречь вычислений). По понятным причинам исследования будем проводить на данных небольшого объёма, стараясь при этом каждый раз экстраполировать результаты в сторону данных бо?льшего размера. В качестве программы для тестирования выберем один из наиболее часто используемых на практике алгоритм решения системы линейных алгебраических уравнений (СЛАУ),  из  возможных реализаций используем прямой (не итерационный) метод Гаусса; в  инсталляционном комплекте http://vbakanov.ru/dataflow/content/install_df.exe (Win'32 GUI) эти файлы программ имеют имена slau_N.set, где N – порядок системы уравнений (число неизвестных); матрицы коэффициентов системы плотнозаполнены.  Т.к. DF-симулятор создавался изначально как исследовательская система, большинство рисунков являются копиями экранов, заранее продуманных и спроектированных исходя из начального замысла.

Эксперимент первый - имеется желание узнать, каким образом распределяется по времени выполнения программы интенсивность вычислений (ИВ, число операций, выполняющихся одновременно)? Для фон-Неймановской машины этот вопрос малоосмыслен (тождественно единица), для современных процессоров с конвейером и несколькими ядрами – чуть более сложен. На рис. ниже показан график функции ИВ для решения СЛАУ 7-го порядка (программный файл  slau_7.set). Представлен, естественно, однозадачный режим выполнения программы, время отложено по оси абсцисс в относительных единицах (тактах, ти?ках).

Как видно, функция ИВ обладает крайне неравномерным (“шквалистым”) характером, отражающим внутренние свойства алгоритма. Проведённая “от руки” огибающая (голубая кривая) имеет характерную форму – резкий подъём вначале с постепенным плавным понижением к концу выполнения программы. Подобная форма кривой ИВ является типовой при вычислениях по  различным алгоритмам (в случае последовательного вычисления кривая ИВ вырождается в прямую-горизонталь). Не наводит ли Вас подобная форма кривой (“несимметричный колокол”) на некие соображения о сущности исследуемого процесса?.. Это, конечно, не Гауссиана (кривая нормального распределения), но при неких условиях  к ней стремится…

Кстати, показанный характер функции ИВ может быть удобен для работы в режиме многозадачности (в основном для выполнения фоновых задач) – для этого необходимо усложнить функционал выходного коммутатора  (для находящихся в очереди ГКВ-команд выделять для исполнения наименее нагру?женные АИУ – т.е. работать “в ложбинах волн”).

Следующий (животрепещущий) вопрос для Исследователя – а как зависит производительность DF-вычислителя от количества АИУ? Очень практическая проблема  – из скольких АИУ должен выбрать Заказчик вычислительную систему для достижения известного ему баланса между производительностью и стоимостью (для решения конкретных задач, разумеется)?

На левом из рис. ниже показана зависимость времени вычислений для различного количества (по оси абсцисс) АИУ; время вычислений (ось ординат) дано в относительных единицах по отношению к максимально возможному.  Правый график показывает величину ускорения (убыстрения)  вычислений в зависимости от числа АИУ (по отношению к последовательному выполнению на одном АИУ). Здесь slau_5.set, slau_7.set и slau_10.set – программы разрешения СЛАУ 5,7 и 10 порядков соответственно.

Представленные на правом графике результаты моделирования небезынтересны – для каждого случая кривые выходят на некое “плато” (показано крупными окружностями) и при дальнейшем увеличении АИУ быстродействие не увеличивается! Напр., для СЛАУ 7-го порядка максимум производительности достигается при числе АИУ, равным 48 (именно этот вариант приведён на предыдущем рисунке); фактически при этим исчерпывается скрытый потенциал рассматриваемого алгоритма (включая размер обрабатываемых  данных).  Это число является внутренним свойством данного алгоритма и ограничивает производительность сверху.

Полученный результат (на первый взгляд) обескураживает – для каждого размера исходных данных (в данном случае – порядка СЛАУ) можно достигнуть только  конечной величины распараллеливания,  причём ограничивается это значение самим алгоритмом (“лучше не получится” при любом, сколь угодно большо?м,  числе АИУ). При таком числе АИУ гарантированно удастся выполнить программу за минимально возможное время.

А какой вид примет функция ИВ при числе АИУ, меньшим минимально необходимого для выполнения с максимальной скоростью? На рис. ниже приведена функция ИВ при числе АИУ, равным 6 (ср. с ранее приведённой кривой для числа АИУ в 48 штук).

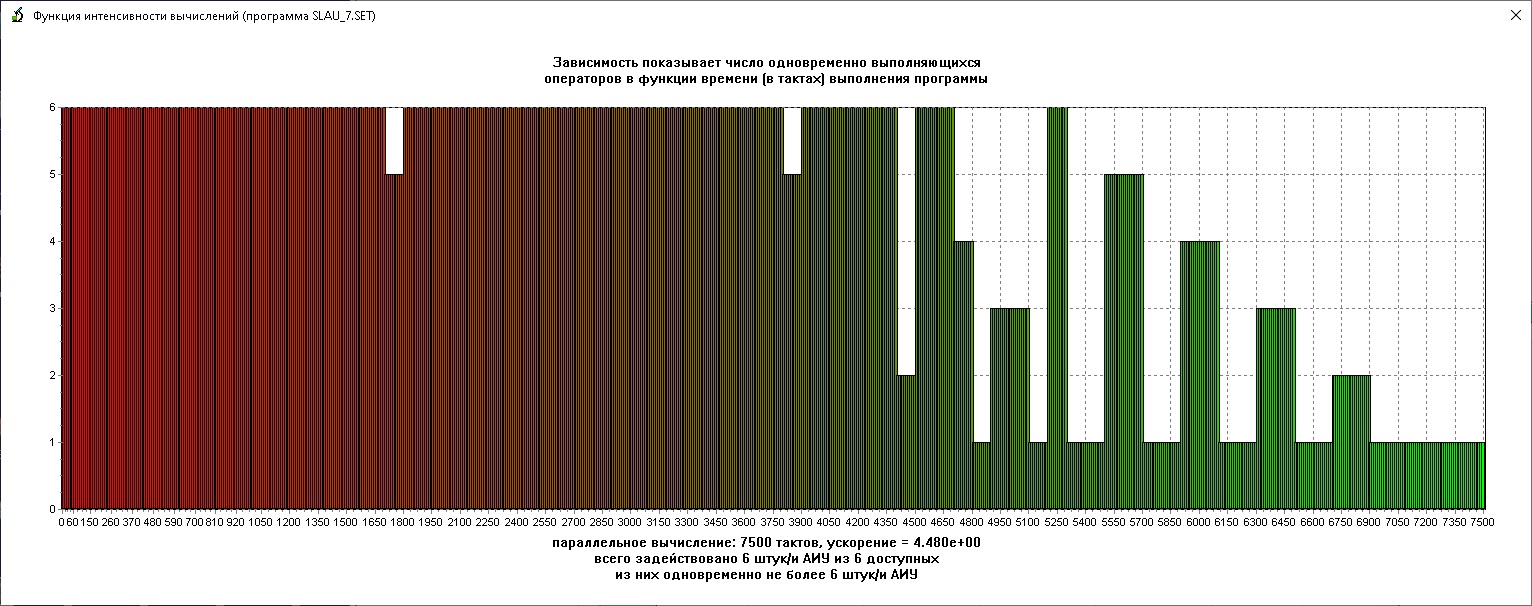
Результат предсказуем – вдоль графика словно хозяйка прошлась скалкой для раскатывания теста, ограничив высоту до 6 (автор иногда бывает привержен “кухонной метафоричности”). При этом DF-вычислитель в процесс выполнения программы формирует соответствующее имеющемуся в наличии числу АИУ расписание выполнения отдельных операторов. При имеющих практическую ценность порядках СЛАУ (напр.,  ?10³)  DF-вычислитель будет работать именно в таком режиме (нелегко представить себе DF-машину с  числом АИУ, превышающем, напр., 10⁶).

Давайте разбираться дальше! Как Вы думаете – есть ли что-то неизменное  между функциями ИВ для одного алгоритма, но разных количеств АИУ? Ну конечно, площадь под кривой одинакова (общее число операторов является инвариантом для каждого размера n обрабатываемых данных). Можно записать (интегрирование ведётся по времени t от t=0 до t=t₀, где t₀  -  момент окончания выполнения программы):

 ? I(n,t) dt=N,

 где I(n,t) - функция интенсивности вычислений, N – общее число операторов в алгоритме при размере (здесь – порядок СЛАУ) обрабатываемых данных n.

Формально это означает, что общее число операторов  неизменно при любой форме функции ИВ (асимптотическая оценка O(n³)). К таким же результатам приводит анализ алгоритма умножения матриц классическим методом (это по сути максимально близкие процедуры). При этом минимальное время выполнения увеличивается линейно (оценка O(n)), но только при условии квадратичного роста   числа АИУ (оценка O(n²)). Имея эти данные, несложно (грубо, конечно) оценить возрастание времени выполнения от числа имеющихся АИУ.   Вдумчивый читатель свяжет эти величины с  высотой и шириной начальной (первообразной, нереформированной) ярусно-параллельной формы информационного графа алгоритма, но временно оставит свои соображения “в уме”, понимая, что автор не желает эти понятия в данной работе использовать.

Общий вид накопительной (кумулятивной) функции ИВ приведён на рис. ниже слева.

Интересно, что обычно рассматривается только функция вычислительной сложности N(n), представляющая собой срез графика вышеприведённого рис. в момент окончания вычислений t=t₀ ; таким образом форма кривой ИВ признаётся несущественной. При описании работы потокового вычислителя естественно расширение понятия  функции вычислительной трудоёмкости в части её изменения в  период выполнения программы.

У пытливого ума возникает вопрос – а можно ли управлять формой кривой ИВ при неизменности всех перечисленных параметров? Это было бы чрезвычайно полезно в условиях многозадачности для выбора режима наилучшего использования ресурса АИУ и трафика  обмена данными внутри DF-машины.

…Подсознательно понятно, что изменением последовательности выполнения операторов (без нарушения информационных связей между ними, конечно!) можно достичь поставленной цели. Но каким образом повлиять на этот параметр?

Один из вариантов – действовать методом целенаправленной настройки приоритетов выборки ГКВ-операторов из буфера команд. Ясно, что такое управление может быть реализовано только в случае, когда число ГКВ-операторов в буфере команд больше, чем количество свободных АИУ (“имеется выбор”) в данный момент.

Выдвинем гипотезу, что в последнем случае добиться управляемости формы графика ИВ можно путём учёта “перспективности”  каждого оператора. В самом деле, чем более направленные в будущее информационные связи оператора способствуют наискорейшему (или наоборот) выполнению программы, тем более/менее он “перпективен” и должен быть выполнен с большим/меньшим приоритетом относительно других.

На рис. ниже слева приведена схема  информационных связей “вперёд” оператора i (от результатов его выполнена зависят операторы 1-j, однако эти операторы зависят по операндам и от иных, отличных от i-того,  операторов). Попробуем выразить признак “перспективности” для i-того оператора количественно.

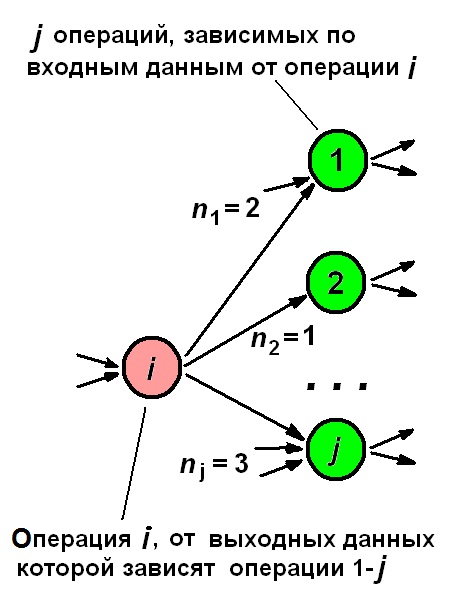
В простейшем случае для оператора i “перспективность” U_i определяется числом операторов, выполнение которых зависит от его выполнения, тогда U_i=j, где j – количество зависимых от i операторов. Однако вес каждого входного операнда у оператора j неодинаков и зависит от их общего числа n_j (обычно n_j=1–2, но в общем случае может быть любым); тогда с учётом весов имеем U_i=? (1/n_j), суммирование идёт по j.

Интересен предикторский подход, учитывающий динамику выполнения процесса вычислений  и число уже “готовых” операндов у каждого оператора j. Если зависящий от i оператор j имеет n_j входных операндов, из которых  уже k_j  “готовы”, то “неготовыми” остаются n_j-k_j и U_i=?((k_j+1)/n_j), причём  суммирование идёт по j (при k_j=0 для каждого оператора j имеем минимальный вес 1/n_j , а при  k_j=n_j–1 вес максимален). Недостатком этого метода является принципиальная невозможность  определения k_j к началу выполнения оператора j, ибо значение k_j  приходится вычислять   раньше (перед выполнением оператора i), а за  время выполнения оператора i могут выполниться другие операторы, увеличивающие  k_j  (т. о. оценка “перспективности” будет пессимистической – за время выполнения оператора i она повысится с ростом k_j у каждого оператора  j).

Пришло время проанализировать результаты вычислительного эксперимента, призванного желанием проверить высказанные идеи. На рис. ниже чёрная  кривая соответствует случаю отсутствия приоритетной выборки ГКВ-операторов из буфера команд  (фактически вариант LIFO), красная – режиму интенсификации, зелёная – депрессии выполнения программы (оси абсцисс и ординат – число АИУ и ускорение вычислений соответственно). Для “чистоты эксперимента” время обработки всех операций задавалось одинаковым.

Относительная величина изменения скорости вычислений невелика (двойной размах изменения 5%), но статистически достоверна. Замечено, что при выполнении программ с большим размером обрабатываемых данных и числом АИУ величина данного явления возрастает.  Адекватность  (соответствие математической модели и физического объекта)  полученных результатов подтверждается пошаговой проверкой аутентичности поведения модели физическим реалиям и целям исследований, применением апробированных алгоритмов и точностью обработки числовых данных.

Для сегодняшних опытов была выбрана программа решения СЛАУ безытерационным методом Гаусса, но можно использовать и более обширную палитру алгоритмов. Замечено, что разные алгоритмы имеют разную степень “управляемости” (в вышеуказанном смысле).

Основой для определения управляемости  может быть уровень связности (“ветвистости”) ИГА конкретной данной программы. Логично разделить (условно) алгоритмы на "легко-" и "трудноуправляемые" (ЛУ и ТУ соответственно). К алгоритмам ЛУ-класса логично отнести алгоритмы, характеризующиеся значительным ветвлением (связностью) ИГА (число зависящих по связи "результат > операнды" от выполнения каждого оператора иных операторов велико), и к классу ТУ в противном случае. В первом случае широк выбор альтернативных путей "захвата" вершин ИГА (выполнения операций), во втором случае он более узок.

Недостатком рассмотренного  метода управления динамикой вычислений является необходимость “просмотра вперёд” информационных связей каждого оператора, что возможно лишь, пожалуй, при использовании быстродействующей ассоциативной памяти в качестве общей.

В ходе экспериментов результаты каждого вычислительного эксперимента тщательно протоколируются и расписание выполнения параллельной программы всегда можно получить численно из лог-файла или качественно просмотреть в окне в форме диаграммы Ганта (на рис. внизу показана диаграмма для решения slau_5.set на 24-х АИУ,  цифры в прямоугольниках – номера операторов).

Жаль, что полученное т.о. расписание параллельного выполнения можно использовать, вообще говоря, только для выполнения на DF-машине. Дело в том, что идеологема VLIW (Very Long Instruction Word, сверхдлинное машинное слово) накладывает дополнительное требование к расписанию – обязательность синхронности начала выполнения всех операций в “связке”. Вдумчивый читатель, однако, без большого труда найдёт выход - полученное расписание будет вполне корректным  и  для VLIW-машины, если назначить время обработки всех операторов одинаковым (для строгости -  максимальным из возможных); именно такой вариант и представлен на рис. вверху.

Итак, мы использовали принцип  потоковых (Data-Flow) вычислений для выявления и исследования определённых свойств алгоритмов. Одним из удивительных явлений при этом является то, что DF-машина не требует (формально, конечно!) каких-либо дополнительных манипуляций со стороны Исследователя (построения графа алгоритма, преобразования его  в ярусно-параллельную форму etc) для обеспечения вполне приемлемого (а в некоторых случаях фактически идеального)  уровня выявления параллелизма в алгоритме и его использования при вычислениях! Десятилетиями при  анализе алгоритмов акцент делался на их свойство “вычислительной сложности”, но дальнейшее изучение свойств алгоритмов (напр., в области  скрытого потенциала параллелизма) без сомнения, подарит нам ещё множество новых ги?тик…