Данная публикация предназначена для Исследователей, которым не жаль с пользой употребить своё время для практического количественного углу́бленного  понимания свойств внутреннего (скрытого) параллелизма в алгоритмах и его, на́йденного параллелизма, рационального использования в вычислительных практиках. Рациональное использование имеющегося в алгоритмах параллелизма определяется набором приёмов, позволяющих получить наиболее приемлемый (по разумным параметрам) план (расписание) выполнения рассматриваемого алгоритма (программы) на заданном поле параллельных вычислителей. Т.к. конечная (реализуемая в процессе собственно вычислений) последовательность выполнения команд неминуемо я́вится всё же несколько иной относительно разработанного на данном этап ие плана вычислений, логично назвать результат данного анализа каркасом плана (расписания) параллельных вычислений.

Алгоритм является результатом разумной деятельности человечества и отражает  в себе (в опосредованном виде, конечно) наиболее глуби́нные, фундаментальные законы развития Природы. Одно это является вполне обоснованной необходимостью исследования характеристик алгоритмов.  

Ряд лет интересом пользовалось изучение параметров вычислительной трудоёмкости (фактически зависимости числа вычислительных операций от размерности обрабатываемых данных) для различных алгоритмов. Параметры параллелизма в алгоритмах – очередная сторона многогранной  сущности “алгоритм”.  В современной ситуации отечественным разработчикам придётся самостоятельно исследовать и решать все связанные с автоматизированной обработкой данных вопросы – время “неограниченной халявы” (когда можно было десятилетиями бездумно копировать западные разработки в области архитектуры и готовых решений аппаратной и программной частей) закончилось.

Определённые знания в области практических технологий параллельного программирования желательны, но не необязательны; предлагаемые исследования предполагают начальный (и, пожалуй, наиболее важный и глубокий этап исследования параллелизма:  анализ “Нача́ла всех Нача́л”  - Его Величества Алгоритма).

Желание выполнять всё более сложные расчёты за минимальное время приводит к требованию повышения производительности вычислительных систем. Из методов повышения производительности в настоящее время отдаётся предпочтения паралелизации. Бесхитростному методу повышения производительности путём повышения тактовой частоты препятствует фундаментальный закон Рэлея (1871), постулирующий четвёртую степень зависимости тепловыделения от тактовой частоты. При этом возможность отвода тепла  затруднительна вследствие малой площади теплового контакта собственно процессора с внешним теплоотводом. При современной кремниевой технологии коэффициент k  в  формуле W≈k×F⁴  равен приблизительно единице  Ватт×ГигаГерц^-4, что ограничивает (по возможностям теплоотвода) тактовую частоту величиной  нескольких гигагерц. Достижения технологии в виде реализации многоядерности позволяют заменить четвёртую степень линейной функцией, однако требуют серьёзных усилий по выявлению и реализации параллелизма.

Задачи связи внутренних свойств алгоритмов с архитектурой вычислительных средств, на которой предполагается выполнять эти алгоритмы, могут быть смоделированы (и, далее, оптимизированы) с использованием компьютерных моделей; см. предыдущие публикации автора.

Автор надеется на всплеск интереса к методам и приёмам разработки системного программного обеспечения (в частности, распараллеливающих блоков трансляторов и интерпретаторов) для него; в этом случае разработка подходов к распараллеливанию будет востребована и, возможно,  позволит избежать ошибок распараллеливающей системы проекта Itanium.

Логично принять, что для исключения какого-либо априорного указания на архитектуру исполняющей среды в формате описания алгоритмов не должно быть явного указания на последовательность выполнения отдельных операторов. Алгоритм при этом представляется в виде “облака операторов”, последовательность же их выполнения определяется информационными причинно-следственными  связями между ними. Такой подход максимально соответствует определению алгоритма как “набора инструкций по преобразованию одних данных в другие за конечное число действий”.

Имея “облако операторов”, остаётся реализовать механизм (аппаратного или программного уровня)  выбора из него допусти́мых (или выбранных по определённому критерию) для исполнения на каждом из (свободных в данный момент) устройств в имеющемся поле параллельных  вычислителей (см. рис. 1).

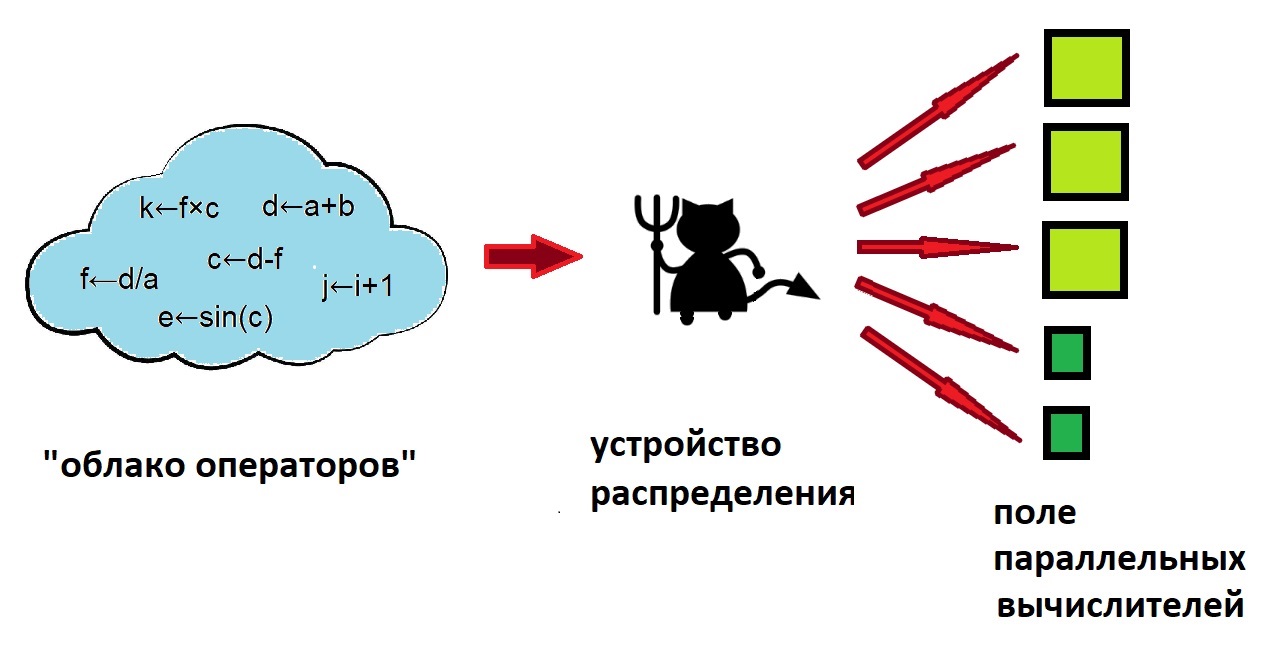
Показанный в центральной части рис. 1 “демон” как раз и олицетворяет наиболее важную часть работы, связу́ющую собственно алгоритм и реализацию его, алгоритма,  параллельного выполнения (существующие, естественно,  обратные связи между “демоном” и другими объектами для упрощения не показаны).

Собственно предлагаемая компьютерная система анализа алгоритмов на наличие внутреннего (скрытого) параллелизма, его параметров и рационального применения найденного параллелизма приведена на рис. 2 (информация о файлах различных указанных расширений будет дана по мере описания).

Программная система включает два модуля – D-F (Data-Flow) и SPF@home, реализована в формате исполняемых файлов формата Win’32, имеет графический интерфейс пользователя (GUI), допускает возможность выполнения в пакетном режиме с командной строкой, является полностью Open Source [1]. Инсталляционные файлы и дополнительные информационные ресурсы свободны для вы́грузки с адресов   [2-4] и   [5-7] соответственно. Дополнительные данные (включая внешний вид пользовательского интерфейса) приведён в вышеназванных публикациях.

Т.к. автор данной публикации задействован в процессе обучения студентов по соответствующей области знаний, он активно  применяет описанное Специализированное Программное Обеспечение (СПО) при обеспечении занятий со студентами и всячески пропагандирует свои разработки в областях обучения и исследований.   

Данная публикация – фактически руководство по проведению исследований в данной области (включая практические примеры планирования и проведения вычислительных экспериментов, представле́ния и анализа полученных данных при  конкретных микроисследованиях). Приведённые разработки могут быть использованы сторо́нними авторами при разработке методических указаний для проведения лабораторных работ (научно-исследовательской работы студентов) по направлениям, связанным с анализом алгоритмов (со стороны потенциала их внутреннего параллелизма) и рационального его, параллелизма, использованию в вычислительных практиках. Надо понимать, что декомпозиция исходной программы на гранулы параллелизма не входит в список задач данной работы.

В целом состав модулей разработанного СПО  выбирался исходя из требований максимального покры́тия существующих принципов выполнения параллельных программ (используемые понятия и термины рассмотрены в предыдущих публикациях автора), см. табл. ниже:

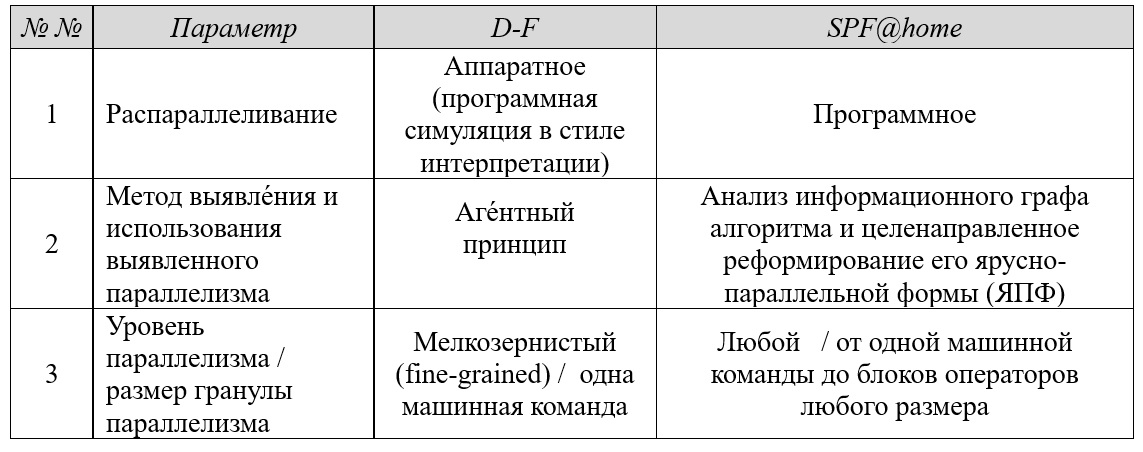
Программный модуль D-F целиком соответствует подходу ILP (Instruction-Level Parallelizm, параллелизм уровня машинных инструкций), модуль SPF@home в полном объёме реализует принцип EPIC (Explicitly Parallel Instruction Computing,  набор инструкций с явным параллелизмом). Рассматривая  сущность “операторы” в программном модуле SPF@home  как группы команд любого размера, этот модуль может быть полезен и при составлении планов параллельного выполнения  программ с гранулами параллелизма бо́льшого размера  – напр.,  автором при проведении занятий эта возможность используется при занятиях на кафедральном вычислительном кластере МИРЭА с использованием технологии MPI (Message Passing Interface, программный интерфейс передачи сообщений).

Заметим, что приём получения и последующего целенаправленного преобразования ЯПФ  является, пожалуй, наиболее  интуитивно  понятным и максимально приближённым к использованию в вычислительной архитектуре VLIW (Very Long Instruction Word, сверхдлинная машинная команда), хотя априори не обеспечивает максимально плотную (по времени) упаковку команд. Обычно “бандл” (bandle, набор отдельных процессорных инструкций в сверхдлинном машинном слове) рассматривается с максимальной степенью аналогии с единичной инструкцией (при обращении  к сабрутинам, обработке прерываний и др.).

Актуальность исследований в области VLIW-архитектур в настоящее время не вызывает сомнений вследствие (очередного) возрожде́ния этой идеологемы. В настоящее время VLIW-подход широко применяется в рыночном сегменте DSP-процессоров  для смартфонов,  систем управления автомобилей, носи́мых устройствах других мобильных систем и в компонентах сетей сотовой связи (архитектура Qualcomm Hexagon QDSP6) !

1. Программный модуль D-F (Data-Flow).

1.1. Общая информация о программном модуле.

Имя исполняемого файла data_flow.exe (PE-формат для Win’32, GUI русскоязычен), имя файла настроек data_flow.ini, контекстная помощь времени выполнения базируется на технологии всплывающих подсказок и WEB-представле́ний. Инсталляция производится c ресурса [2], Исследователь должен ознакомиться с источником [3] и дополнительным тематическим информационным материалом [4].

Т.к. программный модуль data_flow.exe при работе использует некоторые данные с сервера разработчика, будьте готовы при первом запуске программы после сообщения брандмауэра Защитника Windows разрешить до́ступ указанного исполняемого файла к серверу разработчика (впрочем, запрет доступа существенно не ухудшит качество работы программы).

Пользовательский интерфейс программы data_flow.exe  представлен главным окном (слева) и двумя вспомогательными окнами  (справа), рис. 3. Большу́ю роль при моделировании играет цвет (напр., во время выполнения программы содержащие отдельные поля операторов  столбцы таблицы динамически изменяют окраску, отображая этапы поучения ГКВ-статуса как отдельных операндов так и всего оператора и др. показатели выполнения программы).  Цель динамической раскраски – наилучшим образом иллюстрировать основные принципы выполнения программ в пото́ковой вычислительной архитектуре.

1.2. Входные и выходные данные, настройки модуля D-F. 

После инсталляции в текущий каталог добавляются файлы с расширением *.set, представляющие алгоритмы, предлагаемые для исследования.

Для  описания алгоритмов используется ассемблероподобная нотация (порядок операндов соответствует   AT&T-синтаксису) в императивном стиле с сохранением принципа единократного присва́ивания. Любые прямые указания на последовательность выполнения операторов отсутствует (применён принцип “облака операторов”), условность выполнения реализуется предикатным методом.  Список имеющихся алгоритмов приведён в нижерасположенной таблице:

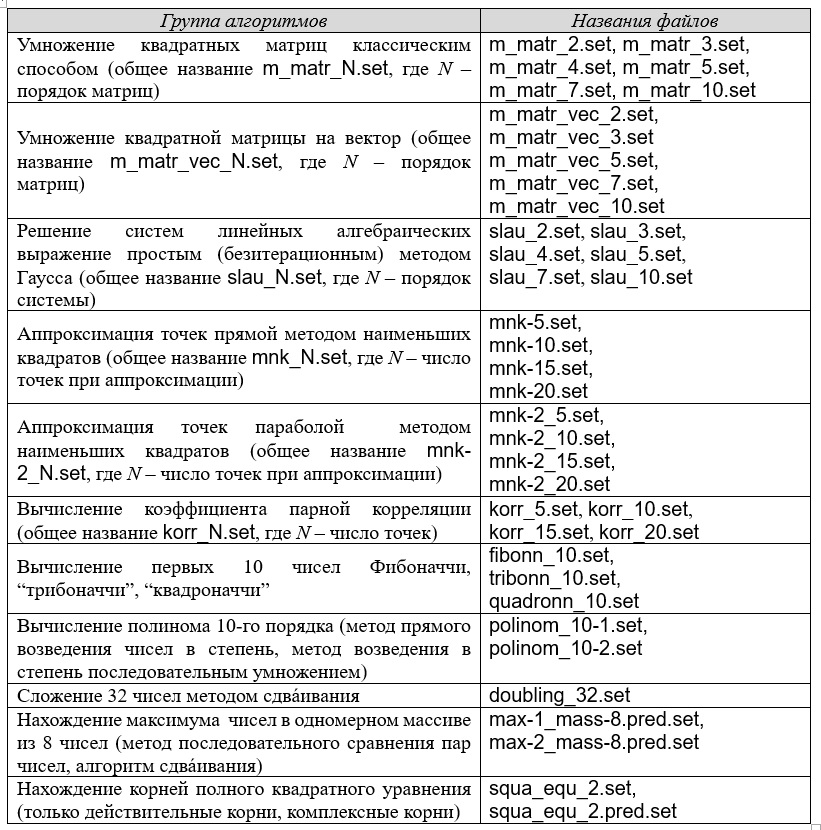
Определённым недостатком исследования является относительно небольшой диапазон размеров обрабатываемых данных, однако такой подход является обычным при невозможности  за ограниченный промежуток времени исследовать большой объём данных, в помощь  исследователю тогда приходит метод выявления тенденций изменения интересующих  величин с экстраполяцией вперёд относительно имеющихся данных.

Кстати, одним из важных (и крайне  полезных для реализации конечных практических целей исследования) явилось количественное доказательство увеличения “пода́тливости” ЯПФ к целенаправленным изменениям с возрастанием размеров обрабатываемых данных. Эта “податливость” (“пластичность”) возрастает с увеличением общего количества операторов даже без изменения собственно алгоритма (следствие параметризорованности информационного графа алгоритма по размеру входных данных); в общем случае “податливость” повышается из-за приращения степеней свободы в допусти́мых положениях операторов по ярусам ЯПФ.

Количественно вариативность (желающие могут использовать термин вариа́бельность) можно оценить относительным числом операторов алгоритма, имеющих возможность располагаться не на единственном ярусе ЯПФ без нарушения причинно-следственных (информационных) cвязей между операторами и величиной диапазона ярусов расположения таких операторов; один из предложенных  вариантов формул для определения величины вариативности приведён в руководстве [6]).

Вы́борка команд из общего пула осуществляется внутренним программным модулем-агентом, сопоставляющем список ГКВ-команд с наличием свободных вычислителей (АИУ, Арифметических Исполнительных Устройств) из заданного списка; при этом (явно) ИГА и ЯПФ не строятся. Пример текста файла slau_equ_2.set (нахождение вещественных корней полного квадратного уравнения) приведён
ниже:

; Решение полного квадратного уравнения (файл squa_equ_2.set)
; в вещественных числах (неотрицательный дискриминант)
; A×X^2 + B×X + C = 0      
; автор - великий индийский астроном и математик БРАХМАГУПТА (7-й век н.э.)
; in case A = 1, B = 7, C = 3
; the solve is: X1 = -0.45862 , X2 = -6.5414
;
MUL A, TWO, A2 ; A2 ← 2 * A ||| #100
MUL A, FOUR, A4 ; A4 ← 4 * A ||| #101
MUL B, NEG_ONE, B_NEG ; B_NEG ← NEG_ONE * B ||| #102
POW B, TWO, BB ; BB ← B^2 ||| #103
MUL A4, C, AC4 ; AC4 ← A4 * C ||| #104
SUB BB, AC4, D ; D[iskriminant] ← BB - AC4 ||| #105
SQR D, sqrt_D ; sqrt_D ← sqrt(D) ||| #106
;
ADD B_NEG, sqrt_D, W1 ; W1 ← B_NEG + sqrt_D ||| #107
SUB B_NEG, sqrt_D, W2 ; W2 ← B_NEG - sqrt_D ||| #108
DIV W1, A2, X1 ; X1 ← W1 / A2 ||| #109
DIV W2, A2, X2 ; X2 ← W2 / A2 ||| #110 
;
SET 1.0, A ; A ← 1.0
SET 7.0, B ; B ← 7.0
SET 3.0, C ; C ← 3.0 
SET 2,  TWO  ; TWO ← 2
SET 4,  FOUR ; FOUR ← 4
SET -1, NEG_ONE ; NEG_ONE ←  (-1) 

При явном задании последовательности выполнения операторов априори определена и последовательность присваивания (логика остаётся на контроле программиста, однако в повторном присваивании всегда скрывается опасность). Для практического программирования требование отсутствия повторного присваивания обычно оборачивается катастрофическим расходом памяти,  при этом роль программ-сборщиков мусора становится чрезвычайно важной. Преимущество работы в режиме однократного присваивания – идеальная возможность отладки (т.к. любой объект является следствием выполнения единственного оператора).

В процессоре Itanium принята идеологема обязательности выполнения всех команд на конвейере, но результат требующей про́пуска команды  теряется. В программном модуле D-F подобный режим также возможен (управляется значением бу́левой переменной SpeculateExec в файле настроек data_flow.ini)

В системе команд симулятора вычислителя потоковой архитектуре флаг-предикат всегда является последним в списке параметров команды (отсутствие предиката интерпретируется как “true”, над предикатами реализованы допусти́мые логические действия (см. [3]).

Формат команды с использованием предиката приведён ниже (файл slau_equ_2.pred.set):

ADD Op1, Op2, Res [, Pred] ; комментарий до конца строки

где ADD – мнемоника команды (здесь - сложение), Оp1 и Оp2 – аргументы команды, Res – результат выполнения команды, Pred – необязательное имя предиката, перед именем предиката допускается символ отрицания ‘!’.

Вариант программы нарождения всех (включая комплексно-сопряжённые) корней полного квадратного уравнения приведён ниже (используется предикат IS_re):

; Решение полного квадратного уравнения
; для получения решения в комплексных числах используем флаг предиката IS_re
; IS_re есть true при значении дискриминанта D>=0 (вещественные корни)
; A×X^2 + B×X + C = 0     
; in case A = 1, B = 7, C = 3
; the solve is: re_X1=-0.45862,im_X1=0; re_X2=-6.5414,im_X2=0
; in case A = 1, B = 3, C = 3
; the solve is: re_X1=-1.5,im_X1=0.866; re_X2=-1.5,im_X2=-0.866 
;
MUL A, TWO, A2  ; A2 ← 2 * A
MUL A, FOUR, A4 ; A4 ← 4 * A
MUL B, NEG_ONE, B_NEG ; B_NEG ← NEG_ONE * B
POW B, TWO, BB ; BB ← B^2
MUL A4, C, AC4 ; AC4 ← A4 * C
SUB BB, AC4, D ; D[iskriminant] ← BB - AC4
;
SQR D, sqrt_D, IS_re ; sqrt_D ← sqrt(D)
ADD B_NEG, sqrt_D, W1, IS_re ; W1 ← B_NEG + D_SQRT
SUB B_NEG, sqrt_D, W2, IS_re ; W2 ← B_NEG - D_SQRT
DIV W1, A2, re_X1, IS_re ; re_X1 ← W1 / A2
DIV W2, A2, re_X2, IS_re ; re_X2 ← W2 / A2 -> re_X2 /; #10 | #110 
;
MUL D, NEG_ONE, NEG_D, !IS_re ; NEG_D ←  NEG_ONE x D
SQR NEG_D, sqrt_D, !IS_re ; sqrt_D ← sqrt(NEG_D)
DIV B_NEG, A2, re_X1,!IS_re ; 1-th root (real)
DIV sqrt_D, A2, im_X1, !IS_re ; 1-th root (img)
CPY re_X1, re_X2, !IS_re ; 2-th root (real)
DIV sqrt_D, A2, W, !IS_re ; temp for im_X2
MUL W, NEG_ONE, im_X2, !IS_re ; 2-th root (im)
;
SET 1, A ; A ← 1
SET 3, B ; B ← 7/3
SET 3, C ; C ← 3
;
SET 2,  TWO  ; TWO ← 2
SET 4,  FOUR ; FOUR ← 4 -> FOUR
SET -1, NEG_ONE ; NEG_ONE ← (-1)
;
SET 0, ZERO ; ZERO ← 0
;
PGE D, ZERO, IS_re ;  IS_re ← “true” if D>=0

Автор ряд лет тщи́тся найти заинтересованных людей, мо́гущих расширить  данный список. На основе каждого алгоритма с помощью модуля D-F возможно  (клавиша F7 главного меню, сохранение в текущем каталоге) сгенерировать файл с расширением *.gv, являющийся описанием Информационного Графа Алгоритма (ИГА) в стандарте языка описания графов DOT. ИГА представляет собой граф, вершинами которого являются операторы, а дугами – связи между последними типа “результат выполнения оператора → входной операнд другого оператора”; этот файл является входной информацией для модуля SPF@home. Все переменные имеют тип double float (целочисленные значения представляются точно).

Команды выполняются в удобном для компьютерной симуляции масштабе времени - время обработки каждой команды задаётся в настроечном файле data_flow.ini. Часть файла настроек с блоком задания времени выполнения отдельных операторов (список см. [3]) в тактах и физического времени собственно такта (приближённое значение вследствие невозможности причисле́ния Windows к системам реального времени) Interval (в мсек) приведена ниже:

[Ticks]
SET=0
ADD=100
SUB=100
MUL=100
DIV=100
DQU=100
DRE=100
SQR=200
SIN=200
COS=200
TAN=200
LOG=200
CPY=10
ABS=2
SGN=2
NEG=2
FLR=2
CEL=2

[Tick_Interval]
Interval=10

Для отладочных целей над загруженной программой предусмотрено выполнение процедур прямой (“результат -> операнды”) и обратной (“операнды -> результат”) трассировок и анализ выполненной части операторов (с текстовой цветовой интерпретацией (главное меню программы).

Результаты полученного плана (расписания) выполнения параллельной программы для данных настроек выдаются графически в виде функции интенсивности вычислений (далее ИВ) - зависимость числа одновременно выполняющихся команд в функции времени;   иногда употребляется акроним DOP (Degree Of Parallelism, степень параллелизма),   графика Ганта (где отдельные работы сопоста́влены с операторами) и в формате текстового файла с именем TPR!уникальные_параметры_эксперимента.txt. Файлы протоколов эксперимента имеют уникальные имена и в текстовом формате сохраняются в подкаталоге Out!Data, дополнительно см. [3].

1.3. Возможные исследования, проводимые с помощью симулятора вычислителя потоковой архитектуры.

1.3.1. Определение минимально необходимого (для данного алгоритма) числа параллельных вычислителей (в условиях неограниченного параллелизма).

Искомая величина определяется экспериментальным путём при задании параметров, имитирующих условия неограниченного параллелизма (НеоП), характеризующимся условием зада́ния числа АИУ, заведомо бо́льшим необходимого для выполнения.

Ход проведения вычислительного эксперимента при этом заключается в загрузке файла заданного алгоритма в программный симулятор, установки априори превышающего минимально необходимое число вычислителей числа АИУ (в  поле ввода в центральной части; не забыть нажать клавишу  Enter для подтверждения ввода) и начале счёта (кнопка Выполнение). Задавать число АИУ можно  порядка десятков/сотен тысяч и миллиона, определяемое число вычислителей будет выдано в верхнем текстовом фрейме в виде строки  “…использовано XXX (мах YYY одновременно) штук/и АИУ из ZZZ доступных” (здесь ZZZ – предварительно заданное число АИУ, небесполезно убедиться, что XXX<ZZZ).

Практическая польза полученных данных – определение верхней границы числа параллельных вычислителей для вновь создаваемого оборудования (для данного алгоритма увеличение АИУ сверх найденного не приводит к возрастанию алгоритма скорости выполнения. Т.о. образом получено важное (являющееся внутренним свойством алгоритма) ограничение области исследования параметров параллелизма для данного алгоритма (нижняя граница, соответствующая последовательному выполнению алгоритма, определяется условием АИУ≡1… рекомендую провести соответствующий эксперимент!).

Интереснейшим исследованием может послужить ответ на вопрос – каким образом зависит определяемой выше минимальное число параллельных вычислителей от размеров обрабатываемых данных (порядка перемножаемых матриц, числа пар точек при обработке статистики etc).

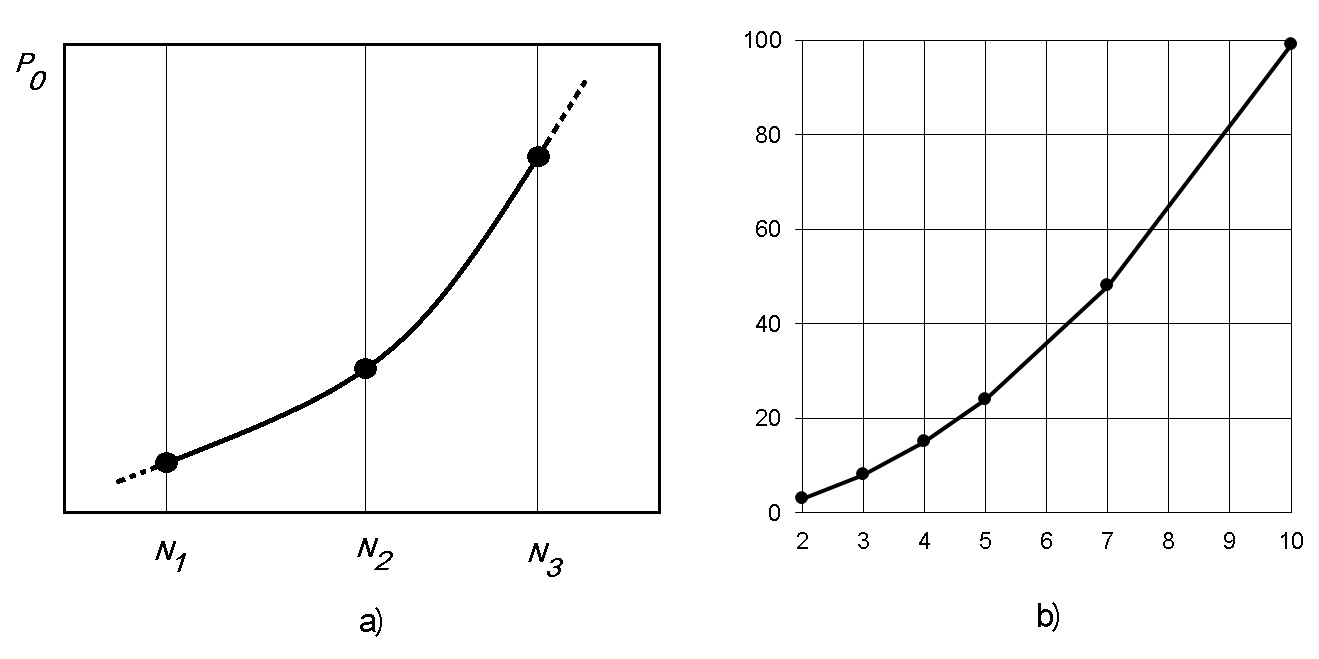
На рис. 4 приведёны графики зависимости  минимального числа параллельных вычислителей Р₀, при котором производительность ещё максимальна, от характеристики размера обрабатываемых данных.

Вопрос к Исследователю -  как Вы думаете, какому закону подчиняется данная функция? Попробуйте следующий ход рассуждений:

• Это (на первый взгляд) линейная функция? Тут всё несложно, но полезно линейность доказать  (средствами Excel, например – см. вычисление коэффициента парной корреляции).

• Нет, это явно нелинейная функция! Возможно, это полиномиальная функция…Но каков порядок полинома?

• Предположим, это полином  2-й  степени. Или 3-й… Как  доказать (или опровергнуть) эту посы́лку (предположение)? Сколько экспериментальных точек необходимо для этого (с помощью Excel аппроксимируйте полученные точки полиномами 2, 3, 4 etc порядков).

1.3.2. Определение времени выполнения алгоритма в функции числа параллельных вычислителей.

Итак, минимально необходимого (для данного алгоритма) числа параллельных вычислителей (в условиях НеоП) нами было определено (это значение ранее обозначили P₀, время выполнения алгоритма при этом t₀). Уже показано, что превышение количества вычислителей сверх P₀ не приводит к увеличению скорости вычислений. Значение P₀ определяется свойствами  алгоритма – быстрее t₀ выполнить его нельзя при любом (сколь угодно большом) числе параллельных вычислителей (это следствие определённой длины критического пути в данном ИГА)!

Возникает практический вопрос, важный при проектировании нового оборудования для параллельных вычислений – насколько время вычислений повышается (а быстродействие t_P/t₀ соответственно, снижается) при выполнении программы на числе вычислителей P<P₀ ? Ясно, что максимальное время выполнения соответствует последовательному выполнению (P=1) и равно сумме времён выполнения всех операторов алгоритма.

Исследователю придётся составить план (вычислительного) эксперимента и провести его, используя симулятор вычислителя D-F; в результате получится нечто похожее на изображённое на рис. 5.

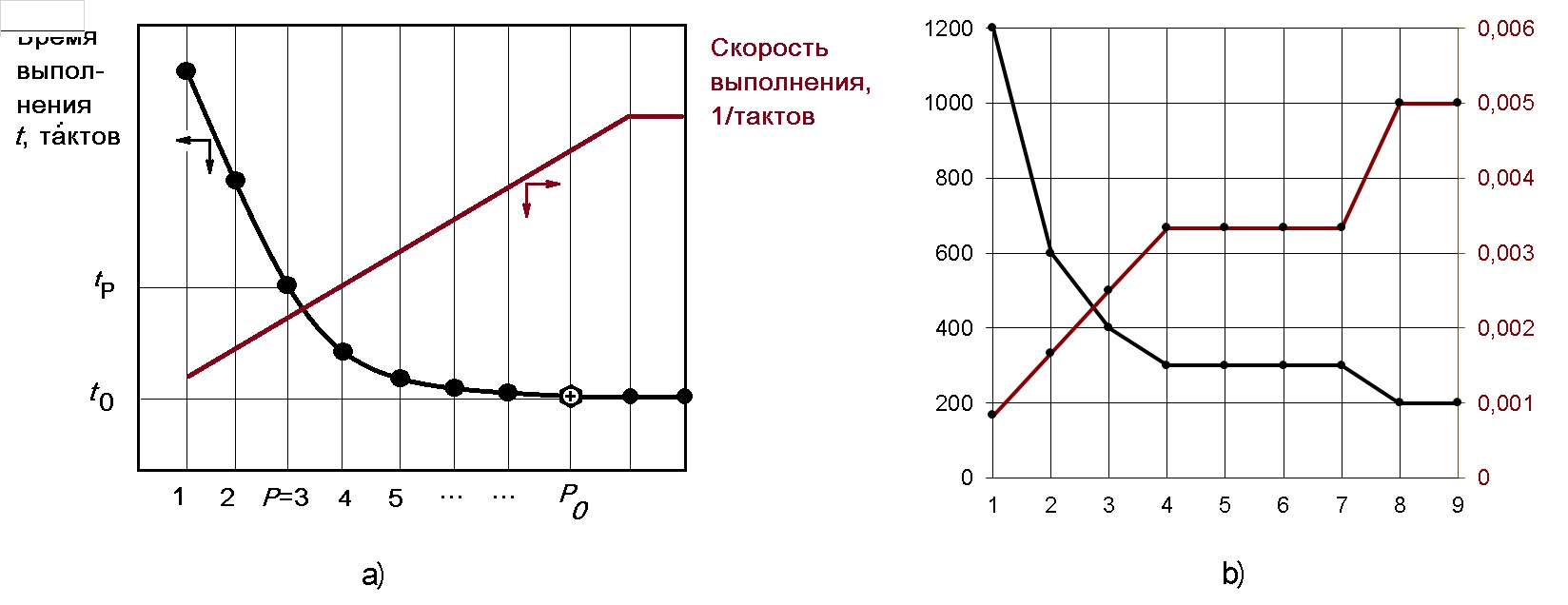
График рис. 5 даёт возможность определить, насколько время выполнения увеличится при любом заданном 1≤P≤P₀ или решить обратную задачу – какое число вычислителей обеспечит производительность 50% от максимальной? 75% от максимальной? Не следует забывать, что число параллельных вычислителей – число целое…

Вопрос Исследователю – какова форма кривой на рис. 5? Подсказка – для данного алгоритма число операторов является инвариантом... Если известен закон изменения функции, не нужно делать много экспериментов – достаточно значений функции в сего в паре точек (напр., при P=1 и P=P₀).

Многое о динамике вычислений может сказать форма кривой ИВ (Интенсивности Вычислений - число одновременно выполняющихся операторов в функции времени выполнения алгоритма), рис. 6 получены копированием соответствующих подокон в системе D-F посредством нажатия клавиш Alt+Print Screen.

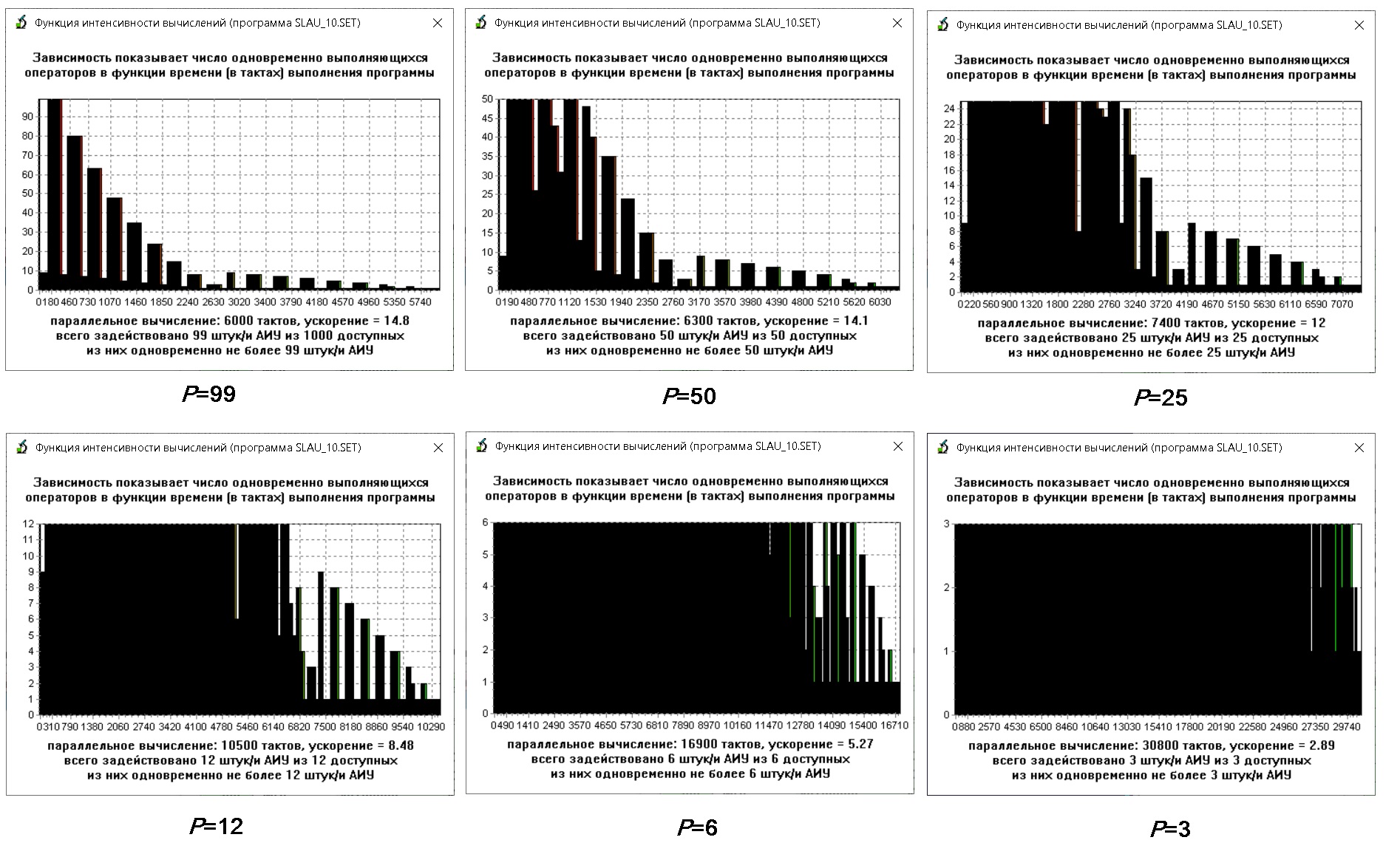
На рис. 6 приведены  функции ИВ для одного алгоритма (slau_10.set – решение системы линейный алгебраических уравнений 10-го порядка прямым методом Гаусса) при разных числах АИУ. Значения числа АИУ (P) указано под  каждым графиком и равно для самого левого верхнего графика P₀=99 (режим НеоП и далее P=50,25,12,6,3 (уменьшение вдвое на каждом шаге). Инвариантом при этом является общее число операторов в алгоритме (интеграл функции интенсивности вычислений по времени), причём среднеингегральное значение определяет коэффициент ускорения выполнения алгоритма (по отношению к последовательному варианту).  При снижении числа вычислителей ниже P₀ график модифицируется путём “прижа́тия” сверху (метафорой может служить раска́тка теста домашней хозяйкой – при снижении толщины теста возрастает его длина).

Легко видеть, что форма кривой ИВ является пилообразной (“шква́льный характер”), а её огибающей – куполообразной (в режиме НеоП) с резким подъёмом и гораздо более плавным спуском по мере выполнения программ (явная аллюзия на кривую Пуассона и принадлежность процедур параллельных вычислений к процессам массового обслуживания). В граничном случае (последовательный характер вычислений) данная кривая вырождается в горизонталь с единичным значением ординаты.

1.3.3. Исследования потенциала ускорения и депресса́ции вычислений на симуляторе потового вычислителя.

Распределением ИВ по времени выполнения программы можно (в определённой степени) управлять путём задания приоритетов выборки ГКВ-команд из входного буфера [3], т.о. замедляя или интенсифицируя процесс вычислений.  Рассматриваемый эффект был найден автором и описан в работе [5].

Инструментом для управления динамикой вычислений при выполнении программы в пото́ковом вычислителей может служит анализ и рациональное использование информационных связей в ИГА (рис. 7). Реализация осуществляется посредством использования буфера ГКВ-команд, расположенным перед входным коммутатором (см. схему в [3]).

Параметрами настройки правил выбора команд из буфера являются:

• Количество параллельных вычислителей (АИУ).

• Правила выборки ГКВ-операторов из буфера команд.

Формально правила выборки операторов настраиваются через файл настроек установкой переменных how_Calc_Param и how_Calc_Prior соответственно в файле настроек data_flow.ini модуля  (подробнее см. [3]).

Результат управления динамикой вычислений показан на рис. 8. В работе [5] показано, что это (найденное путём математического моделирования) явления не является следствием ошибки и количественно возрастает с увеличением размерности обрабатываемых данных.

Приведённые образцы исследований могут быть применены при разработке методических пособий для студентов при изучении данной и смежных областей знания и самостоятельных исследованиях в любых целях. Автор уверен в существовании дополнительных возможностей модуля D-F для исследований в области раскрытия потенциала параллелизма различных алгоритмов и его, параллелизма, рационального использования для вычислительных практик.

2. Программный модуль SPF@home.

2.1. Общая информация о программном модуле.

Имя исполняемого файла spf_client.exe (PE-формат для Win’32, GUI русскоязычен), имя файла настроек spf_client.ini, контекстная помощь времени выполнения базируется на технологии всплывающих окон и WEB-представле́ний. Инсталляция производится c ресурса [5], Исследователь должен ознакомиться с источником [6] и дополнительным тематическим информационным материалом [7].

Т.к. программный модуль spf_client.exe при работе использует некоторые данные с сервера разработчика, будьте готовы при первом запуске программы после сообщения брандмауэра Защитника Windows разрешить доступ указанного исполняемого файла к серверу разработчика (впрочем, запрет доступа существенно не ухудшит качество работы программы).

Пользовательский интерфейс программы spf_client.exe  представлен главным окном (справа) и  вспомогательным окном текстово/графического вывода  (слева, рис. 9).

2.2. Входные и выходные данные, настройки модуля SPF@home.

Файлы основной входной информации имеют расширение *.gv и (обычно) имена, совпадающие с именами set-файлов. GV-файлы могут генерироваться на основе set-файлов программой data_flow.exe  или быть получены  сторо́нними ресурсами.

Пример  файла squa_eq_2.gv приведён ниже:

digraph SQUA_EQU_2 {
100 -> 109 ;
100 -> 110 ;
101 -> 104 ;
102 -> 107 ;
103 -> 105 ;
104 -> 105 ;
105 -> 106 ;
106 -> 107 ;
106 -> 108 ;
107 -> 109 ;
108 -> 110 ;
111 -> 100 ;
111 -> 101 ;
112 -> 102 ;
112 -> 103 ;
113 -> 104 ;
114 -> 100 ;
114 -> 103 ;
115 -> 101 ;
116 -> 102 ;
}

Как видно, gv-файл является текстовым и фактически представляет собой список дуг, образуемых  комплементарными вершинами (операторами) с разделителями-стрелками (указывающими напра́вленность дуги). При генерации gv-файла программой data_flow.exe справа от разделителя (точки с запятой) выдаётся текст двух участвующих в формировании дуги операторов из set-файла (в целях идентификации числового номера оператора с его содержимым).

При использовании модуля SPF@home возможен ручной и автоматический режимы работы.

Ручной режим в основном служит задачам проверки исходных данных,  их несложным преобразованиям в целях подготовки к более глубоким  исследованиям в автоматическом режиме. Например, просмотр ИГА (достигается нажатием F4 с последующим выбором нужного файла) для файла squa_equ_2.gv приводит к выводу текстовом окне (см. рис. 2) такого :содержания

-I- Файл squa_equ_2.gv описания графа успешно прочитан -I-

-=- Дуг ИГА = 21 -=-

#1: 100 -> 109
#2: 100 -> 110
#3: 101 -> 104
#4: 102 -> 107
#5: 102 -> 108
#6: 103 -> 105
#7: 104 -> 105
#8: 105 -> 106
#9: 106 -> 107
#10: 106 -> 108
#11: 107 -> 109
#12: 108 -> 110
#13: 111 -> 100
#14: 111 -> 101
#15: 112 -> 102
#16: 112 -> 103
#17: 113 -> 104
#18: 114 -> 100
#19: 114 -> 103
#20: 115 -> 101
#21: 116 -> 10

Получение ЯПФ  в “верхней” форме (все операторы находятся на ярусах, как можно более прибли́женных к началу выполнения анализируемого алгоритма) реализуется нажатием F5 и приводит к такой выдаче:

Каждая строка выдачи соответствует ярусу ЯПФ и предваря́ется сочетанием “N|M:”, где N – номер яруса, M – число операторов на этом ярусе; номера операторов разделяются пробелом. Находящиеся на нулевом ярусе номера являются входными данными и не учитываются при выполнении большинства операций.

Номера входных операторов предваря́ются символом “«”, после номеров выходных ставится “»”. Режим “приземле́ния”на наинизший ярус выходных операторов, находящихся не на выходном ярусе (возможно при генерации ЯПФ в “верхней” форме) управляется вариантом в подменю главного меню Файлы.

Расположенная в правой части представленного выше изображения  линейчатая диаграмма ширин ярусов (“картинка” копируется в ClipBoard по единократному щелчку “мыши”) выводится в правой части окна тестового вывода, причём фиолетовый и красный цвета соответствуют максимальной  и минимальной ширинам ярусов (дополнительно выдаются в текстовом виде над графиком), пунктиром означается среднеарифметическое значение ширин ярусов данной ЯПФ.  

Для просмотра информационных связей каждого оператора можно использовать F7 или просто щёлкнуть  “мышью” внутри или в непосредственной близости слева или справа от интересующего номера оператора в области вывода ЯПФ, данные выводятся в то же текстовое окно и имеют вид:

ПАРАМЕТРЫ ОПЕРАТОРА 106/4 (#опер/#ярус) для данной ЯПФ:
1. Оператор 106 зависит от 1 оператора/ов:  105/3
2. От оператора 106 зависят 2 оператор/ов:  107/5 108/5
3. Оператор 106 может располагаться на ярусах от 4 до 4 (включительно)
4. Комментарий(*): [[106]SQR D,,sqrt_D,true; sqrt(D) -> sqrt_D] ->
                                 [[107]ADDB_NEG,sqrt_D,W1,true; B_NEG + sqrt_D -> W1]

Максимально полная информация о текущей ЯПФ выдаётся в нижней части текстового окна и имеет такой вид (расшифровку отдельных значений см. в документе [6], выгружаемом на машину Исследователя при инсталляции модуля SPF@home):

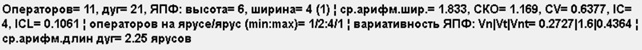
Для просмотра ЯПФ того же ИГА в его “нижней” форме (все операторы находятся на ярусах, максимально приближенных к концу анализируемого алгоритма) используется Ctrl+F5 :

Понятно, что линейчатая диаграмма ширин ярусов ЯПФ – аналог функции интенсивности вычислений из модуля D-F (только полученной  не методами аппаратного распараллеливания, а математическими методами преобразования ИГА в ЯПФ).

Пока мы рассматриваем ЯПФ в условиях НеоП, далее будем решать задачу получения ЯПФ с заданными свойствами. Кстати, высота ЯПФ (число ярусов) в условиях НеоП определяется длиной критического пути в ИГА (т.к. время выполнения алгоритма пропорционально числу ярусов его ЯПФ, для каждого алгоритма имеется ограничение снизу на скорость его выполнения).

Получить диаграмму времени жизни локальных данных можно по F6 (строится по ранее построенной ЯПФ, ниже дана согласно “верхней” ЯПФ для заданного алгоритма):

Локальные данные “живут” между ярусами ЯПФ, поэтому каждая строка начинается символами N1/N2|M:, где N1/N2 – межъярусный промежуток ($ – символ принадлежности выходных данных, являющихся выходными для данной ЯПФ), M – размер локальных данных в условных единицах (величина которых может быть определена ме́рой данной дуги в файле *.med, см. рис. 2). В целом в med и mvr-файлах задаются меры дуг графа, в cls и ops-файлах – параметры вычислителей и операторов (необходимы в случае гетерогенного поля параллельных вычислителей для выбора вычислителей, на которых может быть выполнен данный оператор) соответственно; подробнее о форматах этих файлов и API-функциях их обработки см. [6]).

На следующем рис. представлена та же информация для ЯПФ в “нижней” форме:

В автоматическом режиме преобразования ЯПФ выполняются под  управлением сценариев на языке Lua.

Файлы протоколов эксперимента имеют уникальные имена и в текстовом формате сохраняются в подкаталоге Out!Data [7].

2.3.  Целенаправленное преобразование ЯПФ.

Основная функциональность модуля SPF@home заключается в целенаправленном (цель вырабатывается Исследователем) преобразовании ЯПФ как плана (расписания) параллельного выполнения алгоритма. Собственно ход преобразования контролируется сценарием, выполненным на скриптовом языке Lua. Lua-сценарий составляется и отлаживается исследователем на основе разработанной им цели преобразования ЯПФ. Эта задача является эвристической (творческой) и Исследователь именно так (творчески с учётом особенностей каждого этапа преобразования)  подходит к разработке этапов её решения. Результат применения таким образом составленного сценария не приводит к точному (оптимальному) решению, оправданно назвать полученное решение рациональным.

Архитектура программного модуля SPF@home включает набор интерпретируемых Lua-вызовов, каждый из которых фактически является обёрткой над соответствующей компилируемой C-функцией, подробнее см. руководство  [6]. Редактор исходного текста Lua включает стандартные пользовательские средства редактирования (подсветка ключевых слов, текста API-функций, функции поиска/замены etc).

Пример несложного текста Lua-сценария  приведён ниже (блок копирования ЯПФ из внутреннего представления модуля SPF@home в 2D-массив Lua),  имена  API-функций системы выделены цветом, двойной дефис в Lua служит знаком начала комментария до конца строки:

CreateTiersByEdges("EdgesData.gv") -- создать ЯПФ по файлу
-- EdgesData.gv -- с подтя́нутостью операторов “вверх” 
-- CreateTiersByEdges_Bottom("EdgesData.gv") -- создать ЯПФ по
-- файлу EdgesData.gv -- с подтя́нутостью операторов “вниз” 
--
OpsOnTiers={} -- создаём пустой 1D-массив OpsOnTiers 
for iTier=1,GetCountTiers() do -- по ярусам ЯПФ 
 OpsOnTiers[iTier]={} -- создаём iTier-тую строку 2D-массива OpsOnTiers 
  for nOp=1,GetCountOpsOnTier(iTier) do -- по порядковым номерам
  -- операторов на ярусе iTier 
OpsOnTiers[iTier][nOp]=GetOpByNumbOnTier(nOp,iTier) -- взять номер
-- оператора nOp 
end end -- конец циклов for по iTier и for по nOp

Для выдачи данных о текущей ЯПФ можно использовать функцию Visual (описание функции должно находиться ранее её вызова):

local function Visual() -- визуализация состояния ЯПФ
  PutTiersToTextFrame() -- выдать текстовую информация по ярусам ЯПФ
  PutParamsTiers() -- выдать параметры ЯПФ
  ClearDiagrArea() -- очистить область графической выдачи
  DrawDiagrTiers() -- отрисовать линейчатую диаграмму ширин ярусов ЯПФ
end -- конец функции Visual()

Разработанные (и упомянутые в нижерасположенном тексте публикации) Lua-сценарии преобразования ЯПФ, естественно, не публикуются, ибо являются основной ценностью  (know how) данного приёма исследований. Однако многочисленные (и часто довольно прозрачные) намёки наверняка будут понятны вду́мчивому Исследователю.

В качестве шаблона (один из вариантов)  ниже приведена обобщённая схема  сценария (наивная эвристика с символическим именем BULLDOZER)  целенаправленного реформирования ЯПФ с сохранением высоты ярусов  (список API-вызовов находится в файле [6]).

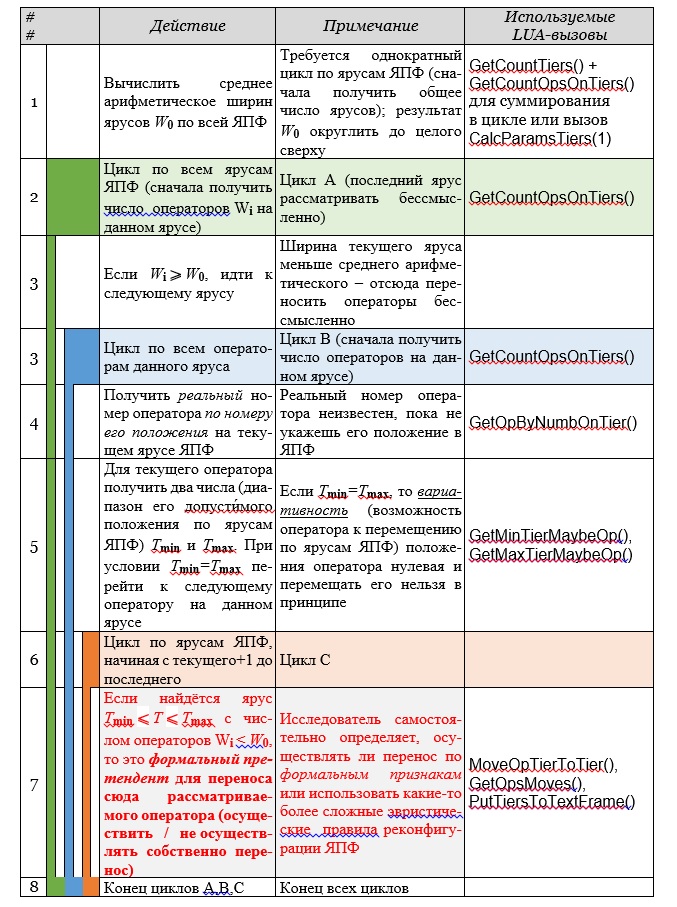
На рис. слева схематично изображено гнездо циклов (циклы А, В и С) с уровнем вло́женности 3  и общим финишем, причём  красным цветом выделена критическая часть (та самая “изюминка”, в конечном счёте определяющая эффективность применения).

Целенаправленные преобразования ЯПФ с  помощью свободно программируемых сценариев  являются частью  известной технологии CMS (Code Morphing Software). Подобный приём относится к “высшему пилотажу” в области анализа и преобразования данных.

Для количественного анализа качества выполненных преобразований (с целью сравнения качества различных эвристик) целесообразно определить некоторые количественные показатели. Такими количественными  параметрами логично установить следующие:

• Вычислительная трудоёмкость преобразования ЯПФ (всегда приятно, когда транслятор работает быстро). В качестве меры вычислительной трудоёмкости выбрано число элементарных действий по модификации ЯПФ (число перемещений операторов с яруса на ярус ЯПФ).     

• Полученная после преобразования ЯПФ плотность кода (уровень использования параллельных вычислителей  в ходе выполнения программы, каждый NOP-оператор на ярусе ЯПФ снижает плотность кода). В качестве меры плотности кода выбран коэффициент вариации ширин ярусов CV=√(⅀((W_i-W̅)²/(H-1)))/W̅, где W_i- ширина i-того яруса ЯПФ, W̅ - среднеарифметическое числа операторов по ярусам, H - число ярусов ЯПФ.

• Вопрос о ме́ре плотности кода представляет особый интерес. В данной работе коэффициент вариации CV в качестве показателя неравномерности ширин ярусов ЯПФ выбран исходя из общепринятости и простоте его интерпретации (лёгкость сравнения отдельных вариантов) в прикладной области исследований. Недостатком CV является его нечувствительность к форме исследуемой кривой (характерной формой огибающей ЯПФ является интенсивный подъём в начале выполнения программы с последующим плавным снижением к концу, такая форма встречается при анализе процессов массового обслуживания).  Программный модуль SPF@home рассчитывает и выдаёт величины неравномерности ширин ярусов ЯПФ во многих формах (включая кривую Лоренца и коэффициент Джини, позволяющие судить о форме анализируемой кривой).

Дополнительными критериями может служить, напр., величина “временно живущих данных” (определяет размер временной памяти – внутренних регистров процессора и/или кэша). Все эти величины, выраженные численно и отдельно или в  свёртке, могут служить критерием оптимальности процесса получения конкретного плана (расписания) выполнения параллельной программы. Т.к. данное исследование не предполагает конкретизации технологии параллельного программирования (работа ведётся на логическом уровне), уместно говорить о каркасе плана (расписания)  выполнения параллельной программы.

Формально логично разделить два случая целенаправленного преобразования ЯПФ с целью получения рациональных планов (расписаний) выполнения параллельной программы – режим сохранения неизменной высоты исходной ЯПФ и режим с возможностью увеличения высоты исходной ЯПФ (высота ЯПФ определяет время выполнения параллельной программы).

2.4. Иллюстрация возможности целенаправленного преобразования ЯПФ посредством выполнения Lua-сценариев

Иллюстрация динамики преобразования ЯПФ с использованием Lua-сценариев приведена на рис. 10 (сравнивается эффективность двух разработанных на языке Lua сценариев, размещённых в файлах 1_Bulldozer.lua и 2_Bulldozer.lua), целевые величины (ординаты графиков) показаны как функции от числа перемещений операторов с яруса на ярус ЯПФ в ходе преобразований. Рис. 10 выпукло иллюстрирует разницу в эффективности двух указанных сценариев. - второй сценарий “медленнее” (требуется большее количество шагов), но конечный результат лучше.

Важным для практики является возможность получения априорной (ещё до проведения собственно преобразования ЯПФ)  информации о самой выполнимости и трудоёмкости преобразования. Т.к. основой реформирования ЯПФ является возможность перемещения (без нарушения информационных зависимостей) операторов с яруса на ярус,  мерой потенциала преобразования выбрана величина “вариативности” (изменения) этих перемещений.

На рис. 11 показана величина “вариативности” V_t (ось ординат), вычисляемая  как усреднённая сумма всех диапазонов возможных перемещений операторов с яруса на ярус данной ЯПФ:

V_t =⅀(H_i^max-H_i^min)/(H-1), ,

здесь H – общее число ярусов,  H_i^max  и H_i^min  - максимальный и минимальный номера ярусов данной ЯПФ, на которых может располагаться i-тый оператор без нарушения информационных связей в ИГА (фактически  диапазон возможного их расположения в единицах ярусов). 

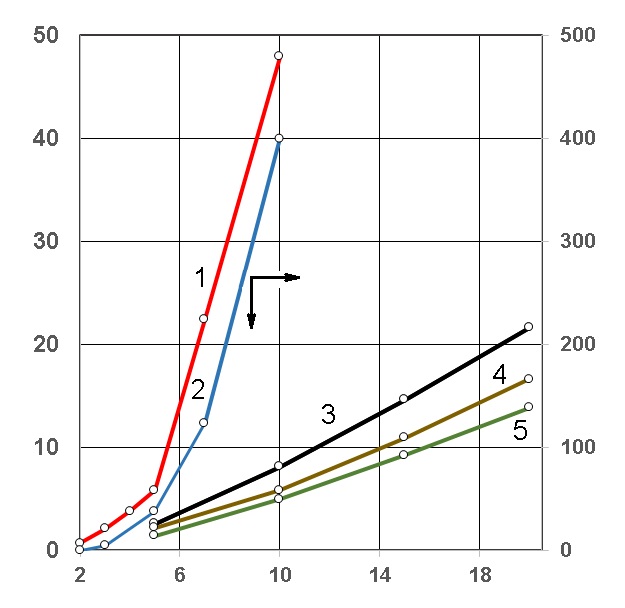
Данные рис. 11 построены в функции единиц размерности обрабатываемых алгоритмом данных (порядок матриц, число пар обрабатываемых статистическими методами чисел). После проведения большой серии опытов применение показателя вариативности в вышеописанном виде оказалось корректным для описания возможности (потенциала) реформирования ЯПФ. 

 Из рис. 11 видно, что вариативность во всех случаях  растёт с увеличением размера обрабатываемых данных, что обещает возможность более эффективного целевого реформирования ЯПФ при увеличении размеров обрабатываемых данных. Т.о. показана возможность получения информации об ЯПФ и преобразования ЯПФ с помощью Lua-сценариев.

2.5. Целенаправленное преобразование ЯПФ без изменения её высоты.

Серьёзной проблемой подхода с использованием ЯПФ является огромная неравномерность в ширинах отдельных ярусов исходной (полученной из ИГА) ЯПФ.

Напр., для ЯПФ перемножения двух квадратных матриц 10-го порядка традиционным способом имеем W=1000 (максимум достигается при H=1), H=10, W̅=190. Для решения СЛАУ 10-го порядка традиционным способом имеем W=99 (максимум достигается при H=2), H=63, W̅_.=14,2. Естественно, хотелось бы иметь число операторов на каждом уровне 190 (в первом случае и 15 во втором). Ограничением являются информационные зависимости в ИГА, не позволяющие произвольно перемещать операторы с яруса на ярус ЯПФ.  Фактически уровень Lua-эвристик определяет качество получения ЯРФ как плана (расписания) выполнения параллельной программы (почти всегда неизвестно уровень качества данного сценария вследствие огромной вычислительной сложности получения оптимального решения).

Автор рекомендует Исследователю тщательно проанализировать подход с использование “нижнего” варианта ЯПФ (напомним, что получение ЯПФ по ИГА в “верхней” или “нижней” формах реализуется API-вызовами CreateTiersByEdges / CreateTiersByEdges_Bottom соответственно). В первом случае превалирующим направлением перемещения операторов являются “сверху вниз”, во втором – “снизу вверх”; вычислительная трудоёмкость получения ЯПФ по ИГА при N операторах одинакова для обоих вариантов и оценивается О(N²).

В случае P (среднеарифметическое значений ширин исходной ЯПФ сравни́мо с числом параллельных вычислителей) возникает задача получения расписания выполнения ПП с максимальной плотностью кода без возрастания высоты ЯПФ (“балансировка” операторов по ярусам ЯПФ).

Основным шаблоном составления Lua-сценариев для этого случая является схема BULLDOZER [7], заключающаяся в достижении ширин всех ярусов ЯПФ, не большей, чем  ⌈W̅⌉. Это соответствует плану выполнения параллельной программы за минимально возможное время на числе параллельных вычислителей ⌈W̅⌉.

Результаты применения Lua-эвристик для данной постановке задачи приведены на рис. 12; обозначения на этом рисунке (по осям абсцисс отложены показатели размерности обрабатываемых данных):

• графики a), b) и с) – ширина ЯПФ, коэффициент вариации (CV ширин ярусов ЯПФ),  число перемещений (характеристика вычислительной трудоёмкости) операторов соответственно;    

• сплошные (красная), пунктирные (синяя) и штрих-пунктирные (зелёная) линии – исходные данные, результат применения эвристик “01_bulldozer” и  “02_bulldozer” cответственно.

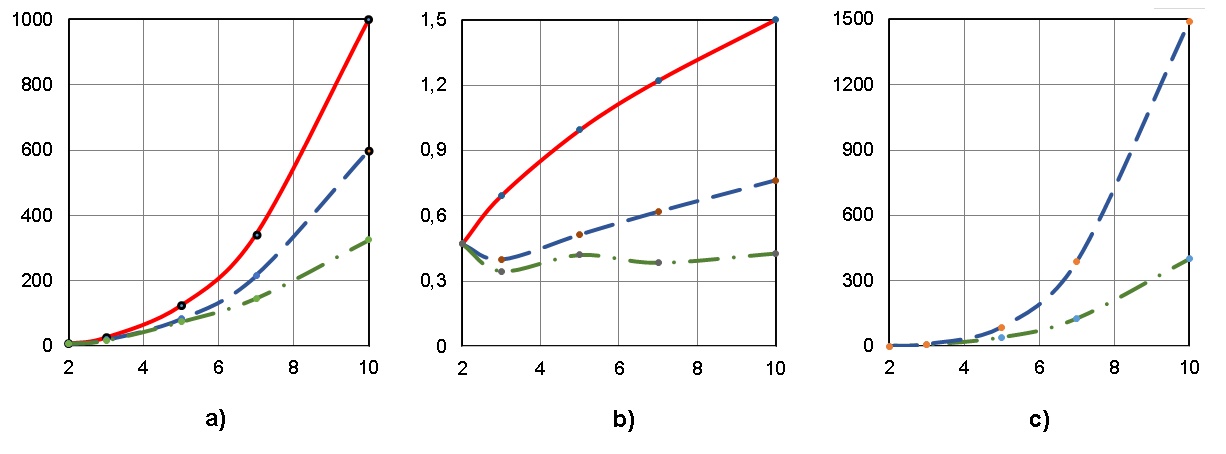
Данные рис. 12 также иллюстрируют возможность совершенствования эвристик в форме Lua-сценариев в области вычислительной сложности икачества получаемых результатов.

Разработанные эмпирические методы по “балансировке” ЯПФ показали противоречивые результаты – в некоторых случаях удавалось достичь  почти 100% плотности кода, а некоторые алгоритмы практически не поддавались указанной модификации (вследствие  ограничений на перемещения операторов между ярусами из-за необходимости сохранения информационных зависимостей в алгоритме).

Применение программного модуля SPF@home возможно и для решения обратной задачи (напр., определение параметров параллельной вычислительной системы исходя из баланса  производительности и стоимости собственно системы).

Вообще говоря, немного алгоритмов подпада́ют под описанные в этом подразделе условия – ширина ЯПФ подавляющего их большинства значительно превышают количество имеющихся в реальных вычислительных системах параллельных вычислителей (о содержащих сотни/тысячи вычислительных ядер арифметических ускорителях фирм nVidia/AMD умолчи́м) и поэтому куда больший практический  вызывает интерес следующий вариант.

2.6. Построение расписания выполнения программ на фиксированном числе параллельных вычислителей при возможности увеличения времени выполнения программы.

В этом подразделе рассматривается наиболее общий случай, соответствующий условию W̅>>P, где P – число параллельных вычислителей; именно при этом приходится увеличивать высоту ЯПФ (а фактически - время выполнения параллельной программы).

Эффективность вышеописанных эвристических методов проверялась путём последовательного их применения к ЯПФ исследуемых алгоритмов в диапазоне числа параллельных вычислителей P от W (ширина исходной ЯПФ) до 1 (полностью последовательное выполнение алгоритма).

Эта постановка задачи максимально близка к реальному случаю составления расписания для VLIW-машины с заданным числом процессорных команд в машинном слове (размер “бандла” сверхдлинного машинного слова). При этом ставится задача и повышения плотности кода

Ниже рассматривается распространенный случай выполнения программы на заданном гомогенном поле из  W параллельных вычислителей (от W=W₀ до W=1, где W₀ – ширина ЯПФ, а нижняя граница соответствует полностью последовательному выполнению). Сравниваем два Lua-сценария реорганизации ЯПФ – “Dichotomy” и “WidthByWidtn”. Особенностью этих  эвристик является правило выбора конкретных операторов,  подлежащих переносу на вновь создаваемые ярусы.

На рис. 13  показаны результаты выполнения указанных эвристик в применении к двум распространенным алгоритмам линейной алгебры - умножение квадратных  матриц классическим методом  и решение системы линейных алгебраических уравнений прямым (неитерационным) методом Гаусса; красные и синие линии на этих и последующих рисунках соответствуют эвристикам “WidthByWidtn” и “Dichotomy” соответственно. Не забываем, что ширина реформированной ЯПФ  здесь соответствует числу команд в “связке” сверхдлинного машинного слова.

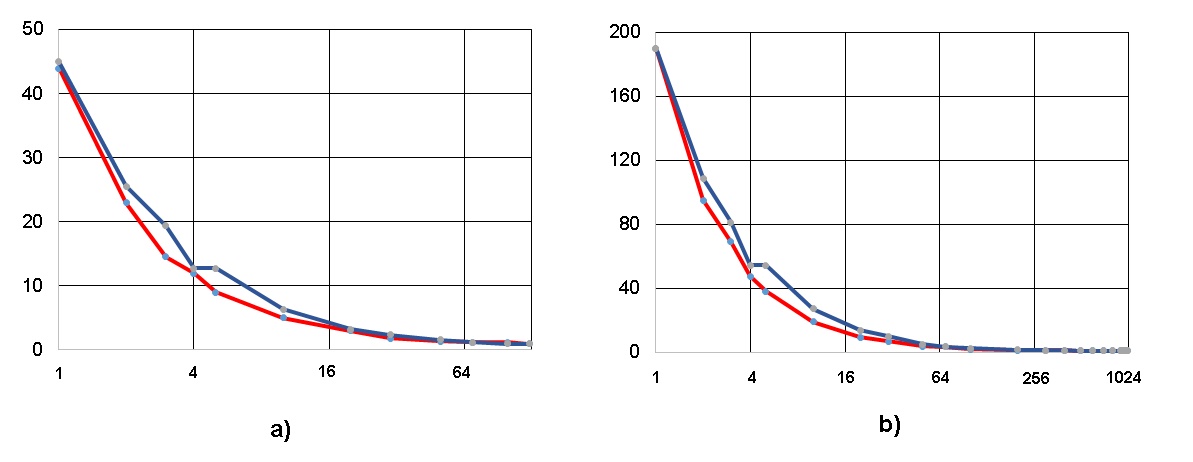
Как видно из рис. 13, оба метода на указанных алгоритмах приводят к близким результатам (из соображений представления ЯПФ плоской таблицей и инвариантности общего числа операторов в алгоритме это, конечно,  гипербола!). При большей высоте ЯПФ увеличивается время жизни данных, но само их количество в каждый момент времени снижается.

Однако “при всех равно-входящих” соответствующие методу (эвристике) "WidthByWidtn" кривые расположены ниже, нежели по методу "Dichotomy"; это соответствует несколько бо́льшему быстродействию. Полученные методом "WidthByWidtn" результаты практически совпадают с идеалом высоты ЯПФ, равным N_сумм./W̅, где N_сумм. – общее число операторов, W̅ – среднеарифметическое числа операторов по ярусам ЯПФ при заданной ширине ея́.

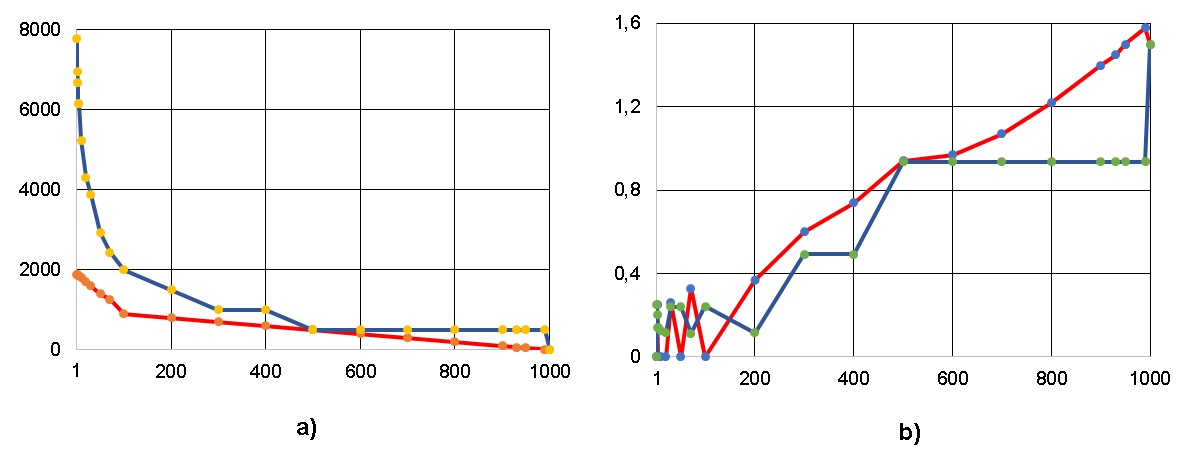
Анализ результатов, приведённый на рис. 14, более интересен (хотя бы потому, что имеет чисто практический интерес – вычислительную трудоёмкость преобразования ЯПФ). Как видно  из рис. 14, для рассмотренных случаев эвристика  "WidthByWidtn" имеет меньшую (приблизительно в 3-4 раза) вычислительную трудоёмкость (в единицах числа перестановок операторов с яруса на ярус) относительно метода “Dichotomy” (хотя на первый взгляд ожидается обратное). Правда, при этом метод  "WidthByWidtn" обладает более сложной внутренней логикой по сравнению с "Dichotomy" (в последнем случае она примитивна). Логично использовать в распараллеливающих компиляторах  метод "Dichotomy" для быстрого (но достаточно “грубого”) построения планов выполнения параллельных программ, а метод "WidthByWidtn" – для построения этих планов в режиме  оптимизации.

2.7.  Построение расписания выполнения параллельных программ на заданном поле гетерогенных вычислителей.

Современные многоядерные процессоры все чаще разрабатываются с вычислительными ядрами различных возможностей. Поэтому практически полезно уметь строить расписание выполнения параллельных программ для подобных систем (с гетерогенным полем параллельных вычислителей). 

В случае гетерогенности поля параллельных вычислителей большая часть работы выполнятся Lua-скриптами (поддержка в виде API-функций системы позволяет производить любые манипуляции с ЯПФ), при этом общий стиль работы скорее  напоминает аге́нтный подход (программный агент из “облака операторов” в пределах каждого яруса ЯПФ распределяет операторы по “подходящим” вычислителям; при этом активно используется информация из файлов *.ops и *.cls).

Модуль SPF@home поддерживает эту возможность путём сопоставления информации из двух файлов – для операторов и вычислителей  (*.ops и *.cls  соответственно, рис. 2). Имеется возможность задавать совпадение по множеству свободно назначаемых признаков для любого диапазона операторов/вычислителей. Условием выполнимости данного оператора на заданном вычислителе является minVal_i≤Val_i≤maxVal_i для одинакового  i (где Val_i, minVal_i, maxVal_i  – числовые значения данного параметра для оператора и вычислителя соответственно).

Разработка расписания для выполнения программы на гетерогенном поле параллельных вычислителей является более сложной процедурой относительно ранее описанных и здесь упор делается на Lua-программирование. Т.к. на одном ярусе ЯПФ могут находиться операторы, требующие для выполнения различных вычислителей, полезной может  служить метафора расщепления ярусов ЯПФ на семейства подъярусов, каждое из которых соответствует блоку вычислителей c определёнными возможностями (т.к. все операторы данного яруса обладают одинаковыми возможностями выполнения, последовательность обработки их в пределах яруса/подъяруса в первом приближении произвольна). На схеме рис. 8 а)  показано расщепление операторов на одном из ярусов ЯПФ в случае наличия 3 параллельных вычислителей 2-х типов, на рис. 15 б) - результат расчёта реального плана выполнения параллельной программы  на гетерогенном поле параллельных вычислителей (3 типа вычислителей по 5,3 и 4 штук соответственно, номера исполняемых операторов скрыты).

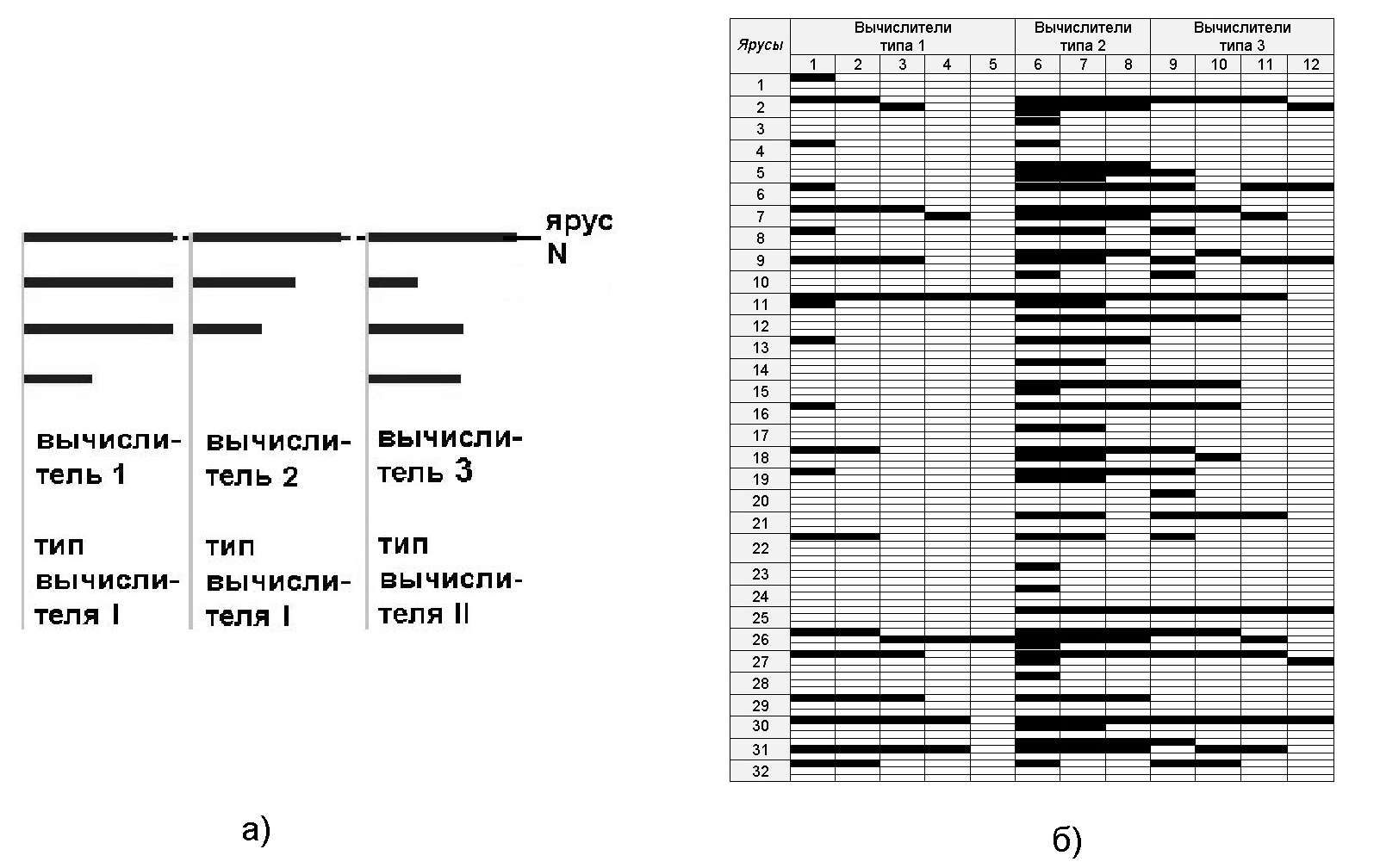
В рассматриваемом случае общее время T решения задачи определяется  суммой по всем ярусам максимальных значений времён выполнения операторов на подъярусах данного яруса, т.к. группы операторов на подъярусах выполняются последовательно (первая сумма берётся по j, вторая – по i, максимум – по k_j): 

T=⅀(max⅀t_ik),

где j - число ярусов ЯПФ, i - число подъярусов на данном ярусе, k_j  -типы  вычислителей на j-том ярусе,   t_ik  -время выполнения оператора типа i на вычислителе типа k. 

Если ставится задача достижения максимальной производительности,   возможно определить число вычислителей конкретного типа,   минимизирующее  T (решение обратной задачи оптимизации по соотношению числа вычислителей разных типов, напр.). Задача минимизации общего времени  решения T усложняется в случае возможности выполнения каждого оператора на нескольких вычислителях вследствие неоднозначности t_ik в вышеприведённом выражении; здесь необходима дополнительная  “балансировка” по подъярусам.

2.8. Период жизни временных данных

Современный вычислитель не может эффективно работать без сверхбыстродействующих устройств временного хранения  данных, разделяемых между отдельными параллельными вычислителями -  кэша и/или регистров общего назначения (оперативная память для этих целей малоприменима вследствие своей медлительности). Эти устройства являются  дорогостоящими  и поэтому оптимизация расписания выполнения алгоритма должна проводиться и по условию минимизации размеров этой памяти.

При выполнении программы непрерывно создаются и “потребляются” промежуточные (временные) данные.  С “точки зрения” ЯПФ эти данные “живут” между ярусами ЯПФ.

Модуль SPF@home включает возможность получать и анализировать (включая построение линейчатых диаграмм) эти данных. Размер данных определяется в единицах некоторых обобщённых величинах, для определения реальных размер данных (напр., в байтах) следует использовать возможности *.med – файлов [6]. В общем случае для генерации данных о расчёте и выводе в текстовое окно временных данных служит API-вызов PutTLDToTextFrame,  для графической отрисо́вки данных – DrawDiagrTLD, сохранение данных в текстовом файле для дальнейшего анализа – SaveTLD (здесь аббревиатура TLD означает Time Live Data, временное хранение данных).

В качестве иллюстрации на рис. 16 приведены данные, доказывающие  саму́ возможность реорганизации плана выполнения алгоритма (программы) в сторону минимизации размеров временнно храни́мых  данных (рассматривается “рабочая лошадка” - ранее анализируемый алгоритм вычисления действительных корней полного квадратного уравнения - файл squa_eq_2.set).  

Слева от диаграмм на рис. 16 показан промежуток ярусов с указанием номеров операторов алгоритма в формате “предыдущий/последующий” (в вышерасположенном исходном коде этого алгоритма рассматриваемые числа располагаются в зоне комментария операторов справа от тройной вертикальной черты, нумерацию начинаем с сотни); in и out – глобальные входные и выходные данные соответственно, в прямоугольниках диаграммы – количество обобщённых данных)

Исследователю будет, несомненно, интересно, что рис. 16  показаны последовательные варианты выполнения данного алгоритма – даже в этом случае возможен выбор более предпочтительных вариантов (по рассматриваемому критерию)!

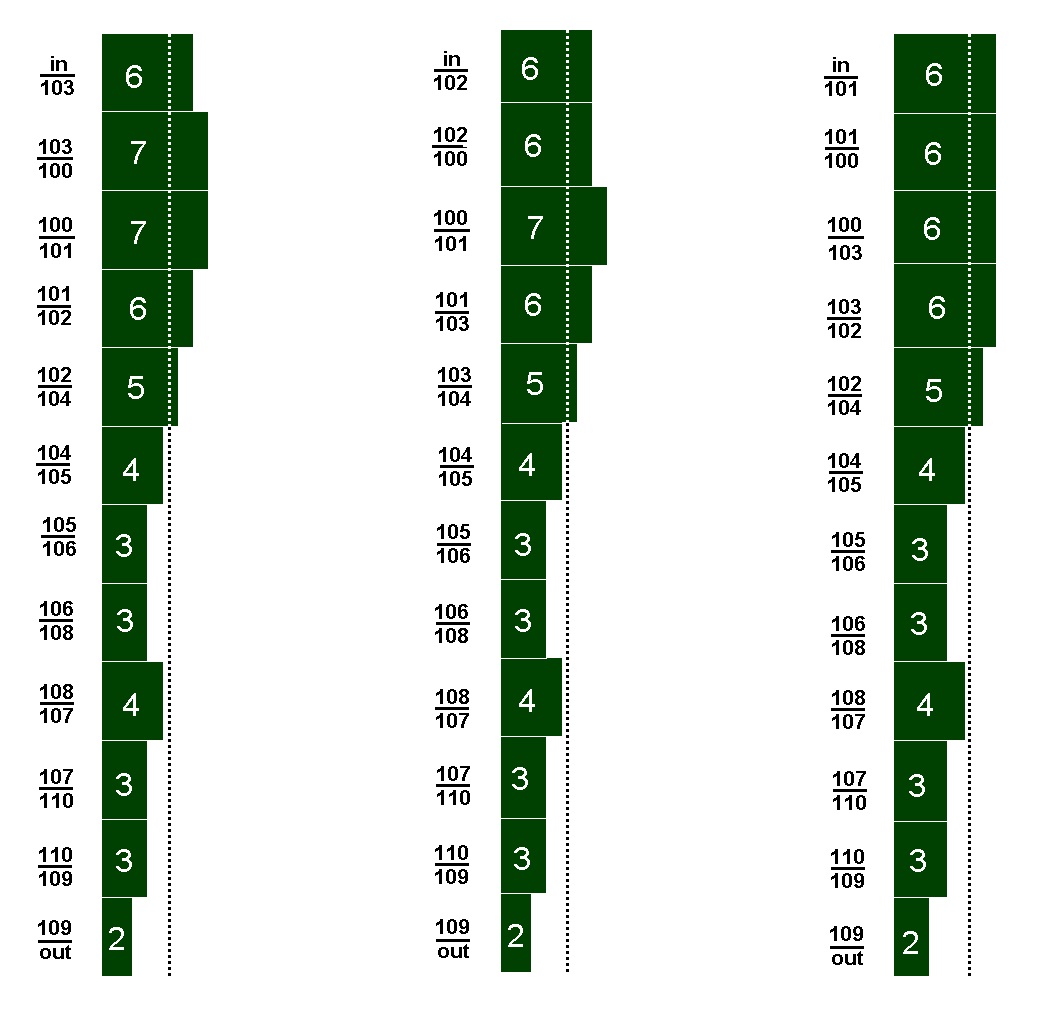
Параметр требуемого при вычислениях объёма данных может быть включён Исследователем в качестве одного из показателей оптимизации вычислений (наряду с плотность кода и вычислительной трудоёмкости получения плана выполнения параллельной программы). Для выбора лучшего варианта при создании специализированного процессора может быть важно отношение объёма внутренних регистров процессора и кэша данных.

Дальнейшее развитие направления, по мнению автора, заключается в разработке автоматического распознава́ния класса  ЯПФ с последующим применением наиболее эффективного для данного случая сценария построения плана выполнения параллельной программы.

Информационные ресурсы:

1. Репозиторий GitHub: https://github.com/Valery-Bakanov/

2. Инсталляционный файл программного модуля D-F: http://vbakanov.ru/dataflow/content/install_df.exe 

3. Руководство пользователя: http://vbakanov.ru/dataflow/content/Base.pdf

4. Информационный ресурс: http://vbakanov.ru/dataflow/

5. Инсталляционный файл программного модуля SPF@home: http://vbakanov.ru/spf@home/content/install_spf.exe

6. Руководство пользователя: http://vbakanov.ru/spf@home/content/API_User.pdf

7. Информационный ресурс: http://vbakanov.ru/spf@home/

---

Предыдущие публикации на тему исследования параметров функционирования вычислительных систем методами математического моделирования:

• Есть ли параллелизм в произвольном алгоритме и как его использовать лучшим образом (https://habr.com/ru/post/530078/, 26.11.2020)

• Такие важные короткоживущие данные (https://habr.com/ru/post/534722/, 24.12.2020)

• Это непростое условное выполнение (https://habr.com/ru/post/535926/, 03.01.2021)

• Динамика потокового вычислителя (https://habr.com/ru/post/540122/, 01.02.2021)

• Параллелизм и плотность кода (https://habr.com/ru/post/545498/, 05.03.2021)

• Сколько стоит расписание (https://habr.com/ru/post/551688/, 10.04.2021)