I. Предисловие

Всё началось с того, что 26 января 2021 года в одноклассниках мне пришло сообщение от Валерия Иванова:

Владимир, в ВА им. Дзержинского вы когда учились и в какой группе?

Я написал Валерию:

1971-1976 г.г. 25 кафедра, НК-25 — Захаров В.Н., начальник курса — п-к Григорьев, курсовой — Кузнецов Ю.М. 1979-1982 г.г. адъюнктура 25 кафедры

И от него пришёл ответ:

Володя, я Иванов Валерий Петрович, сверхсрочник, 23 группа....

Да, я помнил его. Он был единственным сверхсрочником на нашем курсе в Военной Академии им. Ф.Э. Дзержинского (сокращённо ВАД).
В те годы Академия им. Ф.Э. Дзержинского располагалась в столице нашей Родины Городе-Герое Москве на набережной Москвы- реки в Китай-городе:



Между академией и Красной площадью в годы нашей учёбы стояла гостиница Россия, на месте которой сегодня стоит парк «Зарядье». Последний раз я был в Академии в Китайгородском проезде в 2002 году:



Но Военная Академия им. Ф.Э. Дзержинского перестала существовать ещё раньше. Указом президента Российской Федерации от 25 августа 1997 года академия, в целях возрождения исторических традиций российских вооруженных сил и учитывая исключительные заслуги Петра I в создании регулярной армии, переименована в Военную академию Ракетных Войск Стратегического Назначения имени Петра Великого:



К сожалению, в 2015 году «Дзержинка», как её называют по старинке, переехала из центра Москвы в подмосковную Балашиху.
Но я немного отвлёкся. Спустя две недели пришло новое сообщение от Валерия Иванова:

Володя, нас хорошо учили. Я в погонах решал важные и интересные задачи. По увольнении участвовал в создании установки по лечении злокачественных опухолей вихревым магнитным поле. Наша установка лечит людей в Краснодарском диагностическом центре, в Краснодарский мед академии, в Новороссийске, в Армавире,… Работал и в лазерной технике., для систем радиотехники… В составе другой организации участвовал в тендере по разработке системы защиты информации а интересах МВД России… Имею свой взгляд на проблему защиты информации, разработал свою теорию на уровне современного видения с позиции современной эпохи науки.
…
Володя, мои поиски привели меня к фундаментальным основаниям науки и к основаниям защиты информации как области науки, к её аксиомам и её следствиям. Есть моя математическая оценка защищённости информации при применении криптографических средств защиты информации для предельного случая. Пришли мне адрес твоей электронной почты. Мне интересно твоё мнение.
…
Я преподавал в ВУ им. Штеменко, сейчас преподаю в ИМСИТ г. Краснодар… Я преподаю предметы: операционные системы, мат. аппарат при разработке компьютерных сетей, архитектура компьютерных систем...:

Сказать, что нас учили хорошо, — это ничего не сказать. Учили нас по высшему разряду!
Меня заинтриговали его слова «моя математическая оценка защищённости информации при применении криптографических средств защиты информации для предельного случая».
Спустя месяц он прислал мне статью со следующим названием:

К ДВАДЦАТИПЯТИЛЕТИЮ СОЗДАНИЯ АЛГОРИТМА КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ ГОСТ 28147-89

Прочитав статью (особенно не вдаваясь в её название, а именно к двадцатипятилетию), я ответил ему:

В письме от среда, 24 марта 2021 г. 16:50:19 MSK Вы написали:
> — > Валерий Иванов
Очень красиво, Валера! Правда!
Цифры и формулы на твоей совести.
Теперь по существу:
Руководящие документы ФСТЭК России требуют использовать в системах защиты информации алгоритм криптографической защиты информации, определенный ГОСТ 28147-89.
ФСТЭК от криптографии ничего не может требовать — не его епархия. Это ФСБ.
Второе, на смену ГОСТ 28147-89 пришли Magma и Kuznyechik (Магма и Кузнечик).
Хотя магма это практически тот же ГОСТ 28147-89.
Хотя ГОСТ 28147-89 в отличии от ГОСТ Р 34.10-2001 и ГОСТ Р 34.11-94 еще живет. 
Красиво. Можно на Хабр забросить. Разнесут, но ведь это и надо.

И только отправив это письмо, я сообразил, что статья-то написана 7 (семь) лет назад и юбилей был аж в 2014 году. С другой стороны, сам подход очень красив, с моей точки зрения, и его можно применить и к Магме и Кузнечику. И я решил ещё раз уточнить позицию автора по опубликованию статьи на Хабре. И автор ответил:

Валерий Иванов
5 апр в 21:37
Володя, я тебе доверяю….
Володя, на твое усмотрение!….

После этого я окончательно принял решение написать этот материал.
Ниже приводится статья Валерия Иванова (на фотографии справа) без купюр.

II. Оригинал статьи

К ДВАДЦАТИПЯТИЛЕТИЮ СОЗДАНИЯ АЛГОРИТМА КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ ГОСТ 28147-89

ВВЕДЕНИЕ

Руководящие документы ФСТЭК России требуют использовать в системах защиты информации алгоритм криптографической защиты информации, определенный ГОСТ 28147-89. В этом году исполняется двадцать пять лет с начала эксплуатации данного алгоритма, он перешел из второго в третье тысячелетие. Это время сопровождалось ростом вычислительной мощи средств вычислительной техники, которую может привлечь злоумышленная сторона. В силу этого актуальной является задача оценки перспективы использования данного алгоритма взглядом из третьего тысячелетия.
Целью данной статьи является оценка перспективы данного алгоритма с помощью введения в рассмотрение современных представлений физики введением в рассмотрение абстрактного компьютера с предельными техническими характеристиками.

1. Математическая модель оценки защищенности информации криптографическим алгоритмом ГОСТ 28147-89

В нашем случае имеет место процесс взаимодействия объектов – носителей фундаментальных понятий:
— подлежащая защите информация (в зашифрованном виде перехвачена злоумышленниками);
— среда существования информации, включает:

• объект – злоумышленники, расшифровывают перехваченное сообщение;
• объект – зашифрованное согласно ГОСТ 28147-89 сообщение, заставившее злоумышленников производить расшифровку текста путем перебора ключей, определяется количеством операций по перебору всех ключей.
• время, как часы.

Пусть злоумышленники получили возможность использовать средства вычислительной техники максимальной производительности, которые возможны в условиях планеты Земля.
Исследование процесса взаимодействия указанных объектов позволяет обнаружить следующую цепь с конечным множеством состояний:



S₀ — состояние, когда подлежащую защите информацию в период, когда она сохраняла ценность расшифровать не удалось (отрицательный результат для злоумышленников).
S₁ — состояние расшифровки подлежащей защите информации.
S₂ — состояние, когда злоумышленникам удалось расшифровать перехваченную информацию в период времени, когда она сохраняла ценность (положительный результат для ).
Пусть время старения информации характеризуется функцией распределения её старения B(t) с интенсивностью старения — ?.
Переход из состояния S₁ в состояние S₂ определяется интенсивностью расшифровки подлежащей защите информации, определяется функцией распределения расшифровки информации – S(t) с интенсивностью расшифровки — S.
Тогда интервал времени старения перехваченной информация на некотором интервале времени сохраняет ценность составит:


.
Тогда, в случаях экспоненциального распределения как времени старения перехваченной злоумышленником информации, так и времени расшифровки перехваченной информации, вероятность того, что злоумышленникам не удастся расшифровать подлежащую защите информацию до момента, когда информация потеряет ценность, будет определяться следующим математическим выражением:



Численное значение параметра времени старения ? определяет владелец информации, а параметр расшифровки S – производительностью вычислительных средств, которые сумел привлечь злоумышленник.
Перейдем к рассмотрению вычислительного средства, которое может привлечь злоумышленник.

2. Оценка защищенности информации криптографическими средствами защиты информации ГОСТ 28147-89

Введем в рассмотрение некое структурированное материальное образование – абстрактный компьютер, рассмотренный М. Х. Бреммерманном [1,4]. Для решения задачи дешифрирования перехваченного злоумышленником текста компьютер должен обработать N бит. Под «обработкой N бит» будем понимать пересылку N бит по одному или нескольким каналам рассматриваемой вычислительной системы.
Очевидно, что для работы информация должна быть определенным образом физически закодирована. Предположим, что она закодирована в виде энергетических уровней определенного типа энергии в интервале [0, E], где Е – количество энергии, которой мы располагаем для этой цели. Предположим далее, что энергетические уровни измеряются с точностью ?Е.
При этом весь интервал можно разделить максимум на N = E / ?Е равных подинтервалов, причем каждому из них будет соответствовать энергия, равная ?Е.
В случае, когда всегда будет занято не более одного уровня, то максимальное число битов, представимых с помощью энергии Е, будет равно

Для того, чтобы представить большой объем информации при том же количестве энергии, необходимо сократить ?Е. Это возможно только до некоторого предела, так как нужно различать полученные уровни с помощью некоторой измерительной процедуры, которая независимо от ее сути всегда имеет ограниченную точность. Максимальная точность определяется принципом неопределенности Гейзенберга, известного из курса физики: энергия может быть измерена с точностью до ?Е, если выполняется неравенство

где: ?t — длительность времени измерения, h=6,625x10^-27 эрг/сек – постоянная Планка, а ?Е — определяется как среднее отклонение от ожидаемого значения энергии.
Это означает, что количество бит, которые сможет обработать абстрактная ЭВМ на интервале времени ?t составит:

Представим теперь имеющуюся энергию Е соответствующим количеством массы. Тогда, согласно формуле Эйнштейна получаем

где: с = 3x10¹⁰ см/с – скорость света в вакууме.
Таким образом, верхняя, наиболее оптимистическая граница для количества бит – N, которые может обработать СВТ любой природы массой m на интервале времени может быть найдена из выражения:

Подставив значения для с и h и массы m = 1 г, интервала времени, равного 1 с, имеем скорость обработки информации абстрактной ЭВМ массой 1 г:

Отсюда Ханс Бреммерманн сформулировал вывод: Не существует системы обработки данных, искусственной или естественной, которая могла бы обрабатывать более чем 2x10⁴⁷ бит в секунду на грамм своей массы. Данное численное значение можно рассматривать как быстродействие абстрактной вычислительной системы массой 1 г.
В нашем случае под битом будем понимать расшифровываемый текст некоторой длины плюс предполагаемый ключ, на котором зашифрован перехваченный текст. А под обработкой одного бита – операцию расшифровки перехваченного текста с использованием предполагаемого ключа, принятие решения о результатах расшифровки и выбор следующего ключа. Очевидно, что нами злоумышленник поставлен в исключительно комфортные условия.
Известно, что стойкость алгоритма криптографической защиты определяется количеством операций Q, требуемых для перебора ключей. Для рассматриваемого алгоритма Q = 10⁷⁰.
Тогда среднее время перебора всех ключей для абстрактной ЭВМ массой m составит:

а интенсивность дешифрирования:

Для функций дешифрирования и старения, распределенных по экспоненциальному закону, вероятность того, что подлежащая защите информация будет дешифрирована после того момента, когда информация потеряет ценность (после старения информации) будет определяться в соответствии с теорией катастроф, как:

Пусть время старения перехваченной злоумышленником информации определено 30 лет, тогда при условии, что год равен 3.14x10⁷ сек., интенсивность старения перехваченной информации составит:

Пусть требуется обеспечить вероятность исключения дешифрации подлежащего защите текста за время старения, равным 30 лет с вероятностью Р = 0.9999.
Тогда массу вычислительной системы, обеспечивающей соблюдение заданного требования можно определить, из выражения

Подставим в него вычисленные значения ?, а также известное значение Q, получим граничное значение массы абстрактной ЭВМ, ниже которой обеспечивается заданное значение защищенности зашифрованной информации.
В нашем случае тонн, что составляет величину, «неподъемную» не только в настоящее время, но и в отдаленном будущем, поскольку на сегодняшний день самая мощная супер-эвм, эксплуатируемая на Земле, имеет производительность порядка 1000 террафлопс, ее производительность значительно уступает производительности вычислительной системы массой 1г высокоорганизованной материи по Бреммерманну.
Отсюда следует, что рекомендуемый ФСТЭК России алгоритм криптографической защиты информации ГОСТ 28147-89, построенный в опоре на длину ключа, равную 256 бит обеспечивает требуемой уровень защищенности подлежащей защите информации.
При тех же условиях определено требования к стойкости алгоритма шифрования для случая, когда злоумышленная сторона располагает ЭВМ, равной массе планеты Земля: 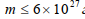. Определено, что длина ключа в этом случае должна составить не менее 293 бита.

Заключение

Автору неизвестны случаи взлома рассмотренного алгоритма, отсюда он полагает, что изложенное выше позволяет сделать вывод о том, что в настоящее время эксплуатируется весьма надежный алгоритм криптографической защиты информации ГОСТ 28147-89, опирающийся на ключ, длина которого обеспечивает необходимую стойкость. Автор также полагает, что данному алгоритму уготована долгая и достойная судьба и в третьем тысячелетии, а его создатели заслуживают большого уважения и признательности их потомков.

Литература

1. Дж. Клир. Системология. Автоматизация решения системных задач. М. Радио и связь. 1990 г.
2. В.П. Иванов. Об основаниях теории защиты информации как внутренне совершенной и внешне оправданной научной теории. Специальная техника №3-4, 2008г.
3. И. Г. Иванов, П.А. Кузнецов, В.И. Попов. Методические основы защиты информации в банковских автоматизированных комплексах. В журнале Конфидент №1, 1994 г.
4. Bremmermann, H, J., Optimization through evolution and recombination. In: Self — Organizing Systems, edited by M.S. Vovits and S. Cameron, Spartan, Washington. D.C. ,1962, pp 93-106.

III.Послесловие

Надо отметить, что В. Иванов не остановился на этом. Вот цитата ещё из одного его письма:

Володя, … я пишу теорию защиты информации на основе современных взглядов на науку. Прикладная наука пытается решить задачи сегодняшнего дня. Нужна теория защиты информации как фундаментальная научная область знаний. Науке наплевать на ФСБ или ФСТЭК. Важна доказательная база оценки стойкости защиты, и ты её увидел. Недавно я встретил своего сослуживца, он академик РАЕН, так он сказал, что наверху склоняются к моему видению (более 30 лет тупика, в котором барахтается защита информации, чему-то должна научить). Защита информации должна стать такой как достойной и результативной как теоретическая физика. Однажды Эйнштейна спросили как новое пробивает себя в науке, он сказал, что новое пробивает себя тогда, когда умирают носители старого! Я наблюдаю это! Основные идеи с философским обоснованием изложены, мне нужно только потерпеть...

И В.Иванов написал очень интересную статью «Об основаниях защиты информации как научной области в современную эпоху науки». Но это тема отдельного разговора.