Введение. Дискретные задачи оптимизации над конечными множествами имеют конечное множество допустимых решений, которые можно перечислять и выбрать из них наилучшее, обеспечивающее получение экстремума целевой функции (ЦФ). Предметная область таких задач - процессы исследования операций (ИО), теория которой формируется уже несколько десятилетий. Методы решения задач, которыми теория располагает сегодня - это, прежде всего, неклассические методы математического программирования, линейное, нелинейное и динамическое программирование, целочисленное и булево, геометрическое и выпуклое программирование, принципы оптимальности, минимаксные и максиминные методы и многие другие. Но среди этого обширного арсенала средств получения оптимальных решений можно выделить один метод, который внес оригинальный взгляд на проблемы оптимизации и позволил по другому воспринимать смысл оптимальности решений.

В самом деле, все рассматриваемые дискретные задачи всегда имеют конечное решение, которое можно получить простым перебором вариантов. Другой вопрос, во что это выльется по затратам и по времени. Поэтому подавляющее большинство методов ИО ориентировано на сокращение переборов, где только это возможно. В разных методах авторам удавалось такой перебор значительно сокращать, либо просто усекать множество вариантов без их детального рассмотрения. Здесь автор предполагает заняться конкретным методом ветвей и границ (МВГ), рассмотреть его возможности и преимущества, указать на имеющиеся недостатки.

В процессе перебора вариантов всегда желательно рассматривать не все из них, а лишь те, которые следует считать перспективными и отбрасывать бесперспективные. Как же осуществлять такой отбор? Где искать оптимальное решение? Частично ответы на эти вопросы были даны в 1960 году авторами  Алисой Лэнд и Элисон Дойг в работе [1]. Эта публикация открыла возможность применения предложенного ими подхода к поиску оптимальных решений многообразных задач комбинаторной и дискретной оптимизации, что позднее стали связывать уже с работами Литтла, Мурти, Суини и Кэрела [2], посвященными специфической задаче коммивояжера [3]. 

Подход получил название метод ветвей и границ (англ. branch and bound) — как общий алгоритмический метод оптимизации. МВГ связывают с деревом поиска оптимального (Т^орt) решения, которое строится в процессе обработки исходных данных задачи. Отсюда названия корень, которому в дереве приписывают все возможные в задаче, решения-ветви, соединяющие узлы дерева, Использование понятия границ и их расчет стимулирует или тормозит рост ветвей в таком дереве. Важную роль играет процедура разбиения на узлы области допустимых решений (ОДР) исходной задачи, т.е. на меньшие непересекающиеся подмножества и их оценивание. Другая процедура, названная процедурой ветвления, реализует разбиение на множества допустимых значений переменной х на подобласти меньших размеров. Еще один важный элемент МВГ - процедура вычисления оценок, которая состоит в поиске значений границ ЦФ для решения задачи. Вычисление нижней границы ЦФ (НГЦФ) является важнейшим, ключевым элементом предложенной схемы. Таким образом, в основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества (стратегия “разделяй и властвуй”) и оценивания получаемых при разбиении частей. Каждый шаг алгоритма разбиения сопровождается проверкой условия того, содержит ли конкретное подмножество оптимальное решение или нет.

Ниже приводится формальная запись сформулированной задачи в понятиях и терминах линейного программирования. Задача линейного программирования после формализации условий и исходных данных, ограничений на переменные может принять следующий вид.

Математическая модель задачи коммивояжера

Сформулированная задача - задача целочисленная. Рассматривается n городов, связанных дорожной сетью. Пусть  х_ij = 1, если путешественник переезжает из i-ого города в j-ый и х_ij =0, если j-ый город не посещается. Условно введем (n+1)-й город, совмещенный с 1-м городом, т.е. расстояния от (n+1)-го города до любого другого, отличного от первого, равны расстояниям от первого города. При этом, если из первого города можно лишь выйти, то в (n+1)-й  город можно лишь прийти. Введем дополнительные целые переменные, равные номеру посещения этого города на пути. u₁=0, u_n+1=n. Для того, чтобы избежать замкнутых путей, выйти из первого города и вернуться в (n+1) введем дополнительные ограничения, связывающие переменные x_ij и переменные u_i (u_i целые неотрицательные числа).

u_i-u_j+nx_ij ? n-1, j=2..n+1, i=1..n, i?j, при i=1 j?n+10?u_i?n, x_in+1=x_i1, i=2..n

Верхняя двойная сумма - целевая функция задачи, для которой наименьшее значение следует отыскивать. Соотношения ниже-ограничения, накладываемые на переменные. Однократные суммы - указывают на требование для занятия единичными элементами плана-решения Х единственной позиции в каждой строке (1? i ? n) и в каждом столбце (1 ? j ? n). Скорее всего, читатели уже встречали название подобной задачи и возможно знакомы с ее историей, содержанием и разновидностями. Мне не хотелось бы вновь поднимать эти моменты и повторяться за другими авторами, но пояснить кратко появление очередной версии статьи все-таки следует. Перед написанием статьи я ознакомился с вариантами текстов из учебных книг и монографий, с теми публикациями, которые выложены в Интернете (не буду их критиковать, в комментариях это уже сделано более чем достаточно), и решил, что все-таки следует написать свой текст, который я смогу рекомендовать для изучения своим ученикам и прочим читателям.

Общая характеристика задачи. Коммивояжёр (фр. commis voyageur) — бродячий торговец посещает населенные пункты (n), связанные разветвленной дорожной сетью, проезд по которой оплачивается отдельно между i-м, j-м пунктами сети. Следуя вдоль маршрута (тура), побывать необходимо в каждом из n пунктов (однократно) и вернуться откуда вышел. Это - формулировка замкнутой задачи, можно не возвращаться в пункт отправления, и задача становится незамкнутая. Симметричная задача. Симметричная проблема коммивояжёра (TSP - traveling salesman problem) возникает, когда стоимость (Сij = Cji ) в оба конца между i-м, j-м пунктами одинакова. Выбор маршрута диктуется затратами, которые торговцем минимизируются. Асимметричная проблема коммивояжёра (ATSP) допускает несимметричность матрицы С_ji ?С_ij. В ещё более общем случае, пути между некоторыми городами могут отсутствовать, а чтобы они не выбирались им вписывают в матрице С_ji =? бесконечную длину). Задача с частичным упорядочиванием (SOP = sequential ordering problem), требующая, чтобы определённый город i был посещён до города j (таких условий может быть несколько). Поиск цикла Гамильтона (HCP = нamiltonian cycle problem) - обнаружение в произвольном графе замкнутых путей, проходящих через каждую вершину в точности один раз. В TSP (симметричной задаче коммивояжёра) путь замкнут и стартовать можно с любого города (и в любую сторону).  Для n городов cуществует (n - 1)!/2 различных путей. Факториал растёт очень быстро: n! ~ nⁿ и пространство в котором ищется оптимальное решение оказывается огромным. Например, для 15 городов существует 43 миллиарда маршрутов и для 18 городов уже 177 триллионов. Именно поэтому задача коммивояжёра интересна и для тестирования различных алгоритмов.

1.Точные методы не только находят некоторое решение, но и при окончании  своей работы доказывают, что это решение - наилучшее. Отметим следующие из них: Полный перебор перестановок n-1 чисел (стартовый город фиксирован). Практически бесполезен при n > 15. Направленный поиск с возвратами - перебор вариантов "относительно" некоторого решения с отсечением путей, имеющих длину большую, чем лучший к текущему моменту путь. Метод ветвей и границ - наиболее эффективный из известных метод отсечения "неперспективных" узлов, за счёт анализа матрицы расстояний. При поиске оптимального решения строится бинарное дерево (в каждом узле порождаются 2 ветви: коммивояжёр идёт в некоторый город или не идёт в него). Линейное программирование применяется для минимизации с ограничениями линейной формы d·x, где x -искомый бинарный вектор размерности n(n-1)/2, компоненты которого x_i равны 1 или 0, в зависимости от того, входит i-я дуга в путь или нет. Вектор d (той же размерности) равен длинам дуг из сети дорог.

2. Эвристические методы: Жадный алгоритм; Метод шнурка; Скользящий перебор; 3. Вероятностные методы: Метод отжига; Генетический алгоритм.  

Модельный полносвязный n-вершинный ориентированный граф (орграф) задачи является таким, что между каждой (i, j) парой вершин существует 2 дуги с разной стоимостью проезда и Сij ? C ji (одностороннее движение).

Таким образом, решение задачи коммивояжёра состоит в отыскании на нашем орграфе маршрута, проходящего однократно через все (n) вершин, при наименьшей его стоимости. Все такие существующие ормаршруты в орграфах называются Гамильтоновыми циклами, которые задаются одноцикловыми перестановками на множестве вершин графа, а для n городов всегда существует ?(n - 1)! различных маршрутов.

Определение 1. Гамильтоновым циклом называется ормаршрут ориентированного графа, включающий ровно по одному разу каждую его вершину, исключая исходную.

Определение 2. Подстановочная матрица - (0, 1) -матрица соответствующая перестановке, цифра позиции которой соответствует строке, а порядковый номер позиции столбцу. Такие матрицы называют диагональными, они реализуют планы ТSP.

Определение 3. Одноцикловой называется перестановка - элемент степени n симметрической группы S_n, которому соответствует один цикл.

Простой пример для 4-х городов. На этом примере покажем и опишем основы МВГ, не решая его. Решение легко получит самостоятельно сам читатель после прочтения статьи. Во всех контрольных положениях МВГ здесь в примере имеются ответы для самопроверки. Вначале покажем сущность процесса решения ЗК со всеми элементами метода ветвей и границ (МВГ), с используемыми понятиями и обозначениями, но без деталей МВГ. На рисунке 1 обозначены: корень дерева поиска оптимального решения: в корне R множество всех допустимых решений R={(1234),(1243),(1432),(1423),(1324),(1342)}; корень содержит все 6 решений - одноцикловых перестановок симметрической группы S_n; другие узлы дерева обозначены символами Х и Y; Х всегда используется как имя текущего обрабатываемого узла; дочерние узлы Х (результаты ветвления) позитивный Y и негативный Y - узел (с подчеркиванием сверху или снизу), в котором алгоритм отказывается осуществлять ветвление (в нем на этом шаге маршрут не наращивается новыми ветвью и узлом).

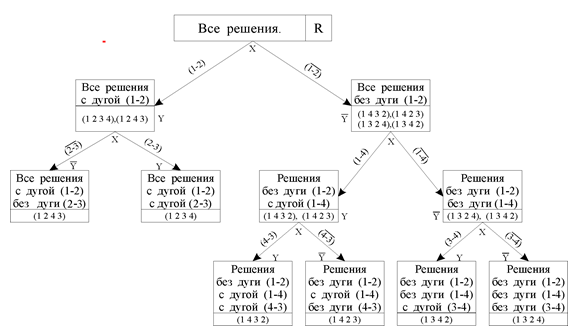
Продемонстрируем ход решения на небольшом примере простым перебором маршрутов. Этот пример призван иллюстрировать общий принцип и понятия МВГ. Детали будут даны ниже с исчерпывающей подробностью. С этой целью сформируем сводную таблицу для дорожной сети из 4-х узлов правая клетка таблицы.

формируется множество S {(i, j)} клеток приведенной матрицы С_[4] с нулевыми значениями. Начинаем строить маршрут (рисунок 1) с вершины 1, включая в него ветвь (1-2), негативную ветвь (1-2) запрещаем включать в маршрут присвоением элементу С₁₂=? большой стоимости. При этом множество решений в корне дерева распадается вначале на два подмножества Y и Y , затем каждое из полученных подмножеств расчленяется на более мелкие и процесс дробления подмножеств решений может продолжаться, пока в каждом из подмножеств не останется по одному решению. Но чаще всего до этого дело не доходит. В процесс вмешиваются другие процедуры и развитие процесса происходит в других направлениях. Иногда начатый маршрут приходится бросать не завершив, и возвращаться к ранее прерванному и остановленному. Дело в том, что при наращивании маршрута отслеживается его качество. Если качество маршрута можно улучшить, возвращаясь к прерванному ранее маршруту, то продолжать ущербный (некачественный) маршрут не стоит. Заметим, что решения задачи моделируются перестановками n вершин (городов), т.е. элементами алгебраической симметрической группы S_n степени n. Не все перестановки являются допустимыми решениями и, конечно, далеко не все среди допустимых будут оптимальными. В симметрической группе подстановок реализуется разбиение на непересекающиеся классы сопряженных элементов. Один такой класс составлен из множество допустимых решений - это класс одноцикловых подстановок, т.е. подстановок образующих цикл, включающий все элементы

Таблица А - Представление множества решений ЗК (n = 4) с их характеристиками

Анализ множества решений ЗК. В таблицу А включены все n!=4! =24 возможных перестановок - решений (Планов Х) задачи, они упорядочены по их лексикографическому номеру. Для каждой перестановки включено ее представление циклами (колонка 3). Например, перестановке (12)(34) в строке 8 соответствуют пары дуг 1> 2 и 1< 2; 3> 4 и 3 < 4, которые не реализуют маршрута (единого цикла). А перестановке (1234) из строки 10 соответствует цепочка 1>2>3>4>1, т.е. получился замкнутый цикл, в который включаются все вершины графа дорог, но однократно. Выбору дуг этого цикла соответствуют элементы матрицы: C₁₂ = 5, C₂₃ = 6 , C₃₄=11, C₄₁= 8. Их сумма - значение ЦФ маршрута ЦФ = 5+6+11+8 = 30. Из n! = 4! =24 перестановок номеров вершин графа путей циклическими (одноцикловыми) являются только шесть (n-1)! =(4-1)! =3!= 6 (их номера 10,11.14, 18,19,23). Маршруты в сети (туры) - допустимые ограничениями модели решения приведены в таблице (3-я колонка выделены жирным шрифтом). Среди них можно осуществить выбор предпочтительного тура. Для каждого из 6 маршрутов подсчитано значение целевой функции (4-я колонка ЦФ: 30,31,55,45,46,45). Среди этих значений наименьшее равно 30. Хотя оно и превышает нижнюю границу ЦФ равную 29. Именно это решение в соответствии с деревом поиска решений на основании приведенной матрицы стоимостей является оптимальным Т^opt= (12)(23)(34)(41) c ЦФ =30.

 Выполняем приведение матрицы стоимостей. Находим коэффициенты приведения каждой строки h_i (выписываем их в строках справа от матрицы) и после этого каждого столбца h_j затем суммируя все h получаем константы приведения всей матрицы

Действительно,  сравнение  Н  с  табличными, полученными методом перебора  оценками  ЦФ  для  всех  туров  показывает,  что  Н  меньше  их  всех.  По  этой  причине  Н  называют  нижней  границей  целевой  функции (НГЦФ),  оценкой  ЦФ  для всего множества  решений  задачи, то есть  для  корневого  узла  дерева (рис. 1).

Пример решения задачи методом ветвей и границ

Исходные данные для задачи коммивояжера.

Число городов n = 5. Граф дорожной сети, связывающей города, полный без петель, ориентированный, несимметричный обыкновенный, задается матрицей С_[5] размера 5?5, дуги графа взвешены; строки матрицы соответствуют пунктам отправления, столбцы - пунктам прибытия. Обозначим начальную (исходную) нижнюю границу целевой функции символом со значением Q*=? – НГЦФ; она служит для сравнения с ней текущих оценок. Как только удается сформировать полный маршрут и вычислить для него ЦФ, Значение Q*=? заменяется на новое, им становится вычисленная ЦФ, с которой далее сравниваются и оцениваются другие маршруты, Н_с= 1+5+6+7+8+3+1 = 31 – значение (оценка) НГЦФ получено как сумма констант приведения строк и столбцов матрицы стоимостей.. Вес дуг (стоимость проезда по дуге) задается элементами С_ij квадратной матрицы. Эта матрица стоимостей С_[5] - основной объект преобразований в задаче. Все диагональные элементы матрицы С_[5] не должны включаться в Т маршрут (в тур), так как соответствующие им дуги - это петли графа и потому им приписаны очень большие стоимости (?). Остальные значения в клетках заполнены подряд следующими натуральными числами (в примере спирально по часовой стрелке от клетки С₁₁=1 к центру матрицы). Работа по поиску маршрута проводится на постоянном графе дорог (с вершинами и дугами) и на последовательно выращиваемом графе дереве (с узлами и ветвями) поиска решений. Текущему узлу дерева поиска решения на каждом шаге алгоритма присваивается имя Х , а узлам-результатам ветвления имя Y– позитивному, включаемому в тур, и имя Y– негативному узлу, не включаемому в Т тур (маршрут).

Многошаговый алгоритм поиска на дереве решений

Успешное решение задачи достигается при обеспечении наличия  хотя  бы  одного  нуля  в  каждой строке  и  каждом  столбце  матрицы С_[5] при их "диагональном" расположении. В этом случае маршрут можно проложить через клетки с нулями и стоимость маршрута будет наименьшей. Далее мы увидим, что такое положение нулей в матрице обеспечивается  многократным применением процедуры приведения матрицы С_[5] и ее преобразованиями, сокращающими размерность до dimС_[5]= 2?2 . В момент достижения матрицей размерности 2?2 она обеспечивает однозначное определение вершин, включаемых в маршрут. Рассматриваются характеристики (d_i, d_j) дуг графа дорог в строке d_i и в столбце d_j изменяющейся матрицы С_[n] стоимостей. Узлы Х дерева разветвляются на "позитивный" и "негативный". Множество висячих «отложенных» узлов (листьев) в дереве решений обозначается символом В, а начальному значению нижней границы целевой функции  задается Q*= ?. Шаги алгоритма бывают двух типов: обыкновенные и с возвращением в отложенный узел; второй тип реализует процедуру "back tracking":

На каждом шаге алгоритма решения задачи коммивояжера выполняются (определяются):

Приведение матрицы С_[i,j] для получения нулевых элементов в каждых ее строке и столбце;

• Формирование множества S клеток с нулевыми значениями в матрице и их характеристик d_i, d_j, ?_ij в форме плоской таблицы;

• Вычисляются max ?_ij и определяется клетка (k, l) с max которая не включается в маршрут;

• Модифицируется матрица: из матрицы удаляются k-я строка и l-й столбец клетки (k, l);

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения;

• В маршрут включается элемент (k, l) с предпочтительной (меньшей) оценкой ?(k, l) НГЦФ

• Сравниваются оценки между собой исходная Q* и вычисленная Н на текущем шаге;

• Вычисляется размерность dimС_[n] матрицы и проверяется равенство этой размерности с dim 2?2;

• Формируется множество В висячих узлов дерева решений с их оценками НГЦФ.

• Приводится фрагмент дерева поиска решений для очередного шага.

Итерационные  шаги: Формирование тура Т начинается выбором 1-й дуги  (k, l) графа дорог  для  включения  её в  маршрут  T, оформляемый как последовательность дуг Т = {(a,b)(c,d)(ef)(hg).....}.

ШАГ 1. Процедура приведения исходной матрицы С_[n] (получение нулей в ней). В  каждой  i-й  строке  С_[n] находим  наименьший  элемент  и  вычитаем  его  из  всех  элементов  строки. Проходим  по  всем  строкам  матрицы. Для такой измененной  матрицы  в  каждом  j-м столбце  опять находим  наименьший  элемент  и  вычитаем  его  из  всех  элементов каждого  j-го  столбца. Проходим  по  всем  столбцам.  Найденные  наименьшие  элементы  называют  константами  приведения  строк  и  столбцов (линий матрицы)  и  обозначают h_i, i =1(1)2n. Константой H_c приведения всей матрицы называют  сумму ?h_i констант линий С_[n]. Эта сумма H_c (С_[5]) = ?h_i =1+5+6+7+8+3+1= 31 является  оценкой  НГЦФ всех решений задачи. Приведение  текущих  матриц С_[n] на шагах алгоритма выполняется   только  в  случае  отсутствия  нулей  в  ее некоторых строках  и/или  столбцах  и новые константы определяются  только  для  таких  линий.

Ниже в таблицах показаны карта дорог, действия и их результаты по приведению матрицы задачи.

Для приведенной матрицы строковые константы h_i приписаны в столбце справа, а столбцовые - в строке снизу матрицы С_[5]. Константа приведения матрицы (С_[5]) = ?h_i =31 вычисляется один раз.

Теперь нули в клетках матрицы имеются во всех строках и столбцах и даже возможно, более чем по одному. К сожалению позиции, занимаемые нулями, не образуют диагонального плана Х. Иначе решением задачи был бы как раз этот план и стоимость соответствующего ему маршрута была бы равна оценке НГЦФ исходной С_[5] матрицы, т.е. Н=31=1+5+6+7+8+3+1.

Формирование множества S нулевых клеток и их характеристик. Перед созданием таблицы S = {(i, j) | C_ij = 0} нулевых клеток выполнено приведение исходной матрицы стоимостей С_[5].

• Формируем множество S из клеток матрицы С_[5] с нулевыми значениями (верхняя строка S={(i,j)}) определяем и вписываем в таблицу значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Для каждой C_ij = 0 клетки приведенной матрицы С_[5] находим d_i - наименьшее значение в строке и d_j - наименьшее значение в столбце, исключая саму C_ij = 0 клетку. Например, для клетки таблицы S(i, j) = (2, 5)= 0 в матрице С_[5] имеем: во 2-й строке (i =2) меньший элемент C_2,1= 6, т.е. d_i = 6. В (j=5) пятом столбце три элемента нули (кроме верхнего), т.е. d_j = 0. На каждом шаге определяется множество клеток S = {(i, j) | C_ij = 0} в приведенной матрице С_[5] стоимостей –  множество  претендентов-дуг для включения первой в оптимальный тур. Общие правила заполнения таблицы S получают вид

• Находим в множестве S клеток матрицы С_[5] с нулевыми значениями ту клетку, которая остальные превосходит по сумме ?_ij = 6 = d_i + d_{j .} Эта клетка аrgmax?_ij = (k, l) = (2, 5);

Вычисляются max ?_ij и определяется клетка (k, l) с max которая включается в маршрут;

Эти значения, например, для клетки (1,2) в первом столбце ?_ij = d_i + d_j =0+2 =2 cуммируются. И для всех нулевых клеток в S для приведенной матрицы С_[5] обрабатываются аналогично. Среди таких столбцовых сумм находится наибольшая и определяется соответствующая максимальной сумме (max?_ij = 6) клетка (k,l), аrgmax?_ij = arg 6 =(k, l) = (2, 5). После того как определены координаты клетки модифицируется матрица С_[5].

Модификация матрицы С_[5] - из матрицы удаляются k-я строка и l-й столбец;

В процессе реализации многошагового алгоритма происходит обработка исходных данных задачи, цель обработки – формирование маршрута однократного обхода вершин графа, моделирующего дорожную карту местности, при наименьшей стоимости маршрута. Маршрут формируется последовательным выбором дуг графа для включения в него. Каждая очередная ветвь дерева решений отыскивается (выбирается) по определенным правилам-ограничениям и при удовлетворении всех ограничений задачи дуга включается в текущий маршрут. Кроме того, реализуется, так называемый «back tracking – поиск с возвращением». Наращивание длины маршрута выполняется с контролем вычисляемого значения целевой функции и условия не превышения ею ранее отложенных промежуточных «оставленных на потом» значений. В случае превышения ЦФ такого значения, алгоритм переходит к продолжению такого отложенного варианта (например, на шаге 4), восстанавливая текущее состояние процесса (матрицы) поиска решения, на момент откладывания решения. Выполняется акт возвращения «вверх» по дереву решений к отложенному ранее варианту (узлу).

• Преобразуем матрицу С_{[5] .} Удаляем строку с номером k = 2 и столбец с номером l =5; при этом размерность матрицы стоимостей изменилась и стала равной (5-1)?(5-1)=4?4; Из матрицы при удалении линий часть клеток с нулевыми значениями может оказаться удаленными; их приходится получать снова;

• Предотвращаем зацикливание, т.е. запрещаем последующий выбор и включение клетки (р, q) в маршрут, где q = k = 2, p = l = 5, a в позицию (l, k) = (5, 2) вписываем большое С_pq =? значение, делая ее запретной для выбора и включения в маршрут. Результаты этих действий отображены в правой матрице С_[4] ниже.

• Вычисляем новую константу приведения матрицы размерностью 4?4, Н =?h_i=4+2=6;

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; Вычисление НГЦФ  для  негативного узла ?(Y) = ?(25) = ?(X) +?(kl) =31 +6 = 37 и вычисление НГЦФ  для  позитивного узла ?(Y) = ?(25) = ?(X) + Н =31 +6 = 37; формулы вычисления различаются, но, тем не менее, оценки иногда совпадают, сравнение оценок показывает, что они в этой ситуации равны. Как поступить, какой узел выбрать? Раз уж формируем маршрут Т, то включаем в него позитивную вершину (2, 5), т.е. тогда T = {(2,5)(..)…}. Задаем соотношением экстремальности выбранному для ветвления узлу (2, 5) новое имя Х = argmin{ ?(Y=(25)) =37, ?(Y=(25)) =37} = (2, 5) или Х = Y(k, l) = Y(2, 5). Этот узел будет ветвиться далее.

• Сравнение текущего значения НГЦФ с исходным значением (Q*=? )? ?(25)=37 ? НЕТ. Вычисляется размерность матрицы (в результате преобразования) и проверяется ее равенство размерности 2?2 = 4?4? Ответ НЕТ.

• В множество висячих узлов В дерева поиска решений включаем узел (Y)=(2,5) с его оценкой НГЦФ =? (25) = 37.

• Фрагмент дерева решений для первого шага принимает вид:

ШАГ 2. Так как ответ на вопрос о размерности матрицы С_[4] на ШАГе 1 отрицательный (НЕТ) переходим к выбору очередного узла (k, l) для включения в маршрут. Матрица стоимостей С_[4] уже сформирована и приведена (ее константа приведения Н = 6, а ее размерность dimС_[4] = 4?4). Все рассуждения 1-го шага остаются справедливыми и для 2-го шага.

• Формируем множество S из клеток матрицы С_[4] с нулевыми значениями, определяем и вписываем в таблицу (как и ранее) значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Формулы обработки элементов матрицы С_[4] остаются без изменения.

• Находим в множестве S клеток матрицы С_[4] с нулевыми значениями то значение, которое превосходит остальные по сумме max?_ij = d_i + d_j =10. Аргументом этой суммы является клетка аrgmax?_ij = (k, l) = (1, 2);

• Преобразуем матрицу С_[4] : удаляем строку с номером k = 1 и столбец с номером l =2; при этом размерность матрицы стоимостей изменилась и стала равной (4-1)?(4-1)=3?3; нулевые клетки в линиях матрицы С_[3] сохранились. Приведение матрицы не требуется, Н =0

• Предотвращаем зацикливание, т.е. запрещаем выбор клетки (р, q), где q = k =1, p = l= 5, a в позицию (l, k) = (5, 1) вписываем большое С_pq =С₅₁=? значение, делая ее запретной для выбора и включения в маршрут. Эти действия отображены в правой матрице С_[3] ниже:

• Вычисляем константу приведения сокращенной матрицы 3?3, Н=?h_i=0+0 =0 ;

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; Вычисление НГЦФ  для  негативного узла ?(Y) = ?(12) = ?(X) +?(kl) =37 +10 = 47 и вычисление НГЦФ  для  позитивного узла ?(Y) = ?(1,2) = ?(X) + Н =37 + 0 = 37; формулы вычисления различаются, оценки на ШАГе 2 уже не совпадают, сравнение оценок показывает, что они в этой ситуации не равны. Какой узел выбрать ? Мы формируем маршрут Т, то включаем в него позитивную вершину (1,2), с меньшей НГЦФT = {(1,2)(2,5)…}. Задаем соотношением экстремальности выбранному для ветвления узлу (1, 2) дерева новое имя Х = argmin{ ?(Y=(1,2)) =47, ?(Y=(1, 2)) =37} = (1, 2) или Х = Y(k, l) = Y(1, 2).

• Сравнение текущего значения НГЦФ с исходным значением (Q*=? )? ?(1,2)=37 ? НЕТ.

• Для вычисленной размерности матрицы проверяется равенство ее размерности 2?2=3?3 ? НЕТ.

• В множество висячих узлов В включаем узел (Y)=(1,2) с его оценкой НГЦФ = ?(12)=47 В = {(25) (1,2)...}

• Фрагмент дерева решений для второго шага принимает вид:

ШАГ 3. Так как ответ на вопрос о размерности матрицы С_[3] на ШАГе 2 отрицательный (НЕТ) переходим к выбору очередного узла (k, l) для включения в маршрут. Матрица стоимостей С_[3] уже сформирована и приведена (константа приведения Н = 0) (ее размерность 3?3).

• Формируем множество S из клеток матрицы С_[3] с нулевыми значениями, определяем и вписываем в таблицу (как и ранее) значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Формулы обработки элементов матрицы С_[3] остаются без изменения.

• Находим в множестве S клеток матрицы С_[3] с нулевыми значениями ту клетку, которая остальные превосходит по сумме max?_ij = 8 =d_i + d_{j .} Аргументом этой суммы является клетка аrgmax?_ij = 8 =(k, l) = (4, 1); в таблице два столбца со значением 8, берем первое;

• Преобразуем матрицу С_[3] : удаляем строку с номером k = 4 и столбец с номером l =1; при этом размерность матрицы стоимостей изменилась и стала равной (3-1)?(3-1)=2?2;

• Предотвращаем зацикливание, т.е. запрещаем выбор клетки (р, q), где q = k = 4, p = l = 1, a в позицию (l, k) = (5, 4) вписываем большое С_pq =С₅₄=? значение, делая ее запретной для выбора и включения в маршрут. Эти действия отображены в правой матрице С_[2] ниже

• Вычисляем константу приведения сокращенной матрицы 2?2, Н=?h_i= 7+0=7

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; вычисление НГЦФ  для негативного узла ?(Y) = ?(4, 1) =?(X) +?(kl)=37+8=45 и вычисление НГЦФ  для позитивного узла ?(Y)=?(4, 1)=?(X) + Н=37 +7 = 44 ; формулы вычисления оценки различны, сравнение оценок показывает, что в этой ситуации меньшее значение НГЦФ имеет ветвь ?(1,2)=44. Поэтому этот узел выбран очередным для маршрута Т ={(4, 1)(1, 2)(2, 5)...}. Задаем соотношением экстремальности выбранному узлу (4, 1) новое имя Х = argmin{ ?(Y = (4, 1))=45, ?(Y=(4, 1)) = 44} = (4,1) или Х = Y(k, l) =Y(4, 1).

• Сравнение текущего значения НГЦФ с исходным значением (Q*=? )? ?(1,2)=44 ? НЕТ.

• Для вычисленной размерности матрицы проверяется ее равенство размерности 2?2=2?2? ДА.

• В множество висячих узлов В включаем узел (Y)=(4,1) с его оценкой НГЦФ =?(4 1)=47 В={(2,5) (1,2)(4, 1) ...} А дальше этот ШАГ имеет отличия от предшествующих.

• Матрица С_[2] стоимостей с размером 2?2 позволяет завершить построение маршрута. Выбранными могут быть только две дуги (3,4) весом 7 и (5,3) весом 0 их и включаем в маршрут, завершая его, Т={(4, 1)(1, 2)(2, 5)(5, 3)(3, 4)} целевая функция этого маршрута определяется суммой ЦФ = 12+1+5+9+17 = 44. Для других маршрутов этот реально просчитанный маршрут может использоваться в качестве нового критерия эффективности (критерия сравнения) и основанием для выбора лучшего маршрута.

• Решение примера позволяет заменить исходную оценку НГЦФ Q*=? на оценку более реальную Q*=ЦФ = 44.

• Фрагмент дерева решений для третьего шага принимает вид:

ШАГ 4. Так как ответ на вопрос о размерности матрицы С_[3] на ШАГе 3 положительный (ДА) в алгоритме решения задачи происходит ряд изменений. Завершился поиск одного из вариантов (1-го) маршрута с оценкой НГЦФ, которая стала критериальной (Q*=44). Переходим к ответу на вопрос следует ли искать другие маршруты и окажутся ли они лучше найденного? Ответ на вопрос помогает указать множество В отложенных решений с оценками НГЦФ и запомненными состояниями. Если среди отложенных имеется оценка НГЦФ меньшая найденной ?=44, то возможно, продолжая расчет по этой ветви дерева, в итоге получим другой маршрут, лучше уже найденного, а при анализе всех отложенных решений будет найден оптимальный (неулучшаемый) маршрут. Действуем дальше так. В множестве В среди отложенных имеется оценка w = 37 < 44, которая соответствовала отказу на ШАГе 1 от выбора узла (k, l) =(2,5) для включения в маршрут. Матрица стоимостей в той ситуации была приведенная С_[5]. Мы возвращаем в матрицу дугу (2,5), но запрещаем ее выбор, полагая С₂₅ =?, при котором в строке 2 матрицы С_[5] пропадает нулевая клетка. Ее возврат оценивается как h_i = 6, для 2-й строки, что увеличивает прежнюю оценку НГЦФ. Остальные нули в С_[5] сохраняются. Последовательность маршрута - пуста, не содержит ни одной дуги. Константа приведения матрицы Н = 6

• Формируем множество S из клеток матрицы С_[5] с нулевыми значениями, определяем и вписываем в таблицу (как и ранее) значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Формулы обработки элементов матрицы С_[5] остаются без изменения.

• Находим в множестве S клеток матрицы С_[5] с нулевыми значениями ту клетку, которая остальные превосходит по сумме max?_ij = 4 = d_i + d_j . Аргументом этой суммы является клетка аrgmax?_ij = 4 = (k, l) = (3, 5);

• Преобразуем матрицу С_[5] : удаляем строку с номером k = 3 и столбец с номером l = 5; при этом размерность матрицы стоимостей изменилась и стала равной (5-1)?(5-1)=4?4; при этом пропала нулевая клетка в 4-ой строке.

• Предотвращаем зацикливание, т.е. запрещаем выбор клетки (р, q), где q = k = 5, p = l = 3, a в позицию (l, k) = (5, 3) вписываем большое С_pq =С₅₃=? значение, делая ее запретной для выбора и включения в маршрут. Эти действия отображены в правой матрице С_[4] ниже

• Вычисляем константу приведения сокращенной матрицы 4?4, Н=?h_i= 2+0=2;

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; вычисление НГЦФ  для негативного узла ?(Y) = ?(3, 5) =?(X) +?(kl)=37+4=41 и вычисление НГЦФ для  позитивного узла ?(Y)=?(3, 5)=?(X) + Н=37 +2 = 39 ; сравнение оценок показывает, что в этой ситуации меньшее значение НГЦФ имеет ветвь ?(3,5)=39. Поэтому этот узел выбран очередным для включения в маршрут Т ={(3, 5) ....} Задаем соотношением экстремальности выбранному для ветвления узлу (3, 5); новое имя Х = argmin{ ?(Y = (3, 5))=41, ?(Y=(3, 5)) = 39} = (3,5) или Х = Y(k, l) =Y(3, 5).

• Сравнение текущего значения НГЦФ с исходным значением (Q*=44 )? ?(3,5)=39? НЕТ.

• Вычисляется размерность матрицы и проверяется равенство ее размерности 2?2=4?4? НЕТ.

• В множество висячих узлов В включаем узел (Y)=(3, 5) с его оценкой НГЦФ =?(3 5)=41 В={(35) ...}

• Фрагмент дерева решений для четвертого шага принимает вид:

ШАГ 5. Так как ответ на вопрос о размерности матрицы С_[4] на ШАГе 4 отрицательный (НЕТ) переходим к выбору очередного узла (k, l) для включения в маршрут. Матрица стоимостей С_[4] уже сформирована и приведена (коэффициент приведения Н = 2) (ее размерность 4?4).

• Формируем множество S из клеток матрицы С_[4] с нулевыми значениями, определяем и вписываем в таблицу (как и ранее) значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Формулы обработки элементов матрицы С_[3] остаются без изменения.

• Находим в множестве S клеток матрицы С_[4] с нулевыми значениями ту клетку, которая остальные превосходит по сумме max?_ij = 8=d_i + d_{j .} Аргументом этой суммы является клетка аrgmax?_ij = (k, l) = (4, 1);

• Преобразуем матрицу С_[4] : удаляем строку с номером k = 4 и столбец с номером l =1; при этом размерность матрицы стоимостей изменилась и стала равной (4-1)?(4-1)=3?3; пропала клетка с нулевым значением во 2-й строке

• Предотвращаем зацикливание, т.е. запрещаем выбор клетки (р, q), где q = k = 1, p = l = 4, a в позицию (l, k) = (4, 1) вписываем большое С_pq =С₄₁=? значение, делая ее запретной для выбора и включения в маршрут. Эти действия отображены в правой матрице С_[3] ниже

• Вычисляем константу приведения сокращенной матрицы 3?3, Н =?h_i= 3+0 = 3 ;

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; вычисление НГЦФ  для  негативного узла ?(Y) = ?(4,1) = ?(X) +?(kl) =39 +8 = 47 и вычисление НГЦФ  для  позитивного узла ?(Y) = ?(4,1) = ?(X) + Н =39 +3 = 42 ; формулы вычисления различаются, оценки на ШАГе 5 не совпадают, сравнение оценок показывает, что они в этой ситуации не равны. Как поступить, какой узел выбрать ? Мы формируем маршрут Т, включаем в него позитивную вершину (4,1), с меньшей НГЦФ T = {(4,1)(1,2)…}. Задаем соотношением экстремальности выбранному для ветвления узлу (4,1) новое имя Х = argmin{ ?(Y=(4,1)) =47, ?(Y=(4, 1))=42}=(4, 1) или Х = Y(k, l)=Y(4, 1).

• Сравнение текущего значения НГЦФ с исходным значением (Q*=44 )? ?(4,1)=42 ? НЕТ.

• Вычисляется размерность матрицы и проверяется ее равенство размерности 2?2=3?3? НЕТ.

• В множество висячих узлов В включаем узел (Y)=(4,1) с его оценкой НГЦФ =?(41)=47 В = {(35) (4,1)...}

• Фрагмент дерева решений для пятого шага принимает вид:

ШАГ 6. Так как ответ на вопрос о размерности матрицы С_[4] на ШАГе 5 отрицательный (НЕТ) переходим к выбору очередного узла (k, l) для включения в маршрут. Матрица стоимостей С_[3] уже сформирована и приведена (Н = 3) (ее размерность 3?3).

• Формируем множество S из клеток матрицы С_[3] с нулевыми значениями, определяем и вписываем в таблицу (как и ранее) значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Формулы обработки элементов матрицы С_[3] остаются без изменения.

• Находим в множестве S клеток матрицы С_[3] с нулевыми значениями ту клетку, которая остальные превосходит по сумме max?_ij = 4 = d_i + d_{j .} Аргументом этой суммы является клетка аrgmax?_ij = (k, l) = (5, 4);

• Преобразуем матрицу С_[3] : удаляем строку с номером k = 5 и столбец с номером l =4; при этом размерность матрицы стоимостей изменилась и стала равной (3-1)?(3-1)=2?2;

• Предотвращаем зацикливание, т.е. запрещаем выбор клетки (р, q), где q = k = 4, p = l = 5, a в позицию (l, k) = (5, 4) вписываем большое С_pq =С₅₄=? значение, делая ее запретной для выбора и включения в маршрут. Эти действия отображены в матрице С_[2] ниже

• Вычисляем константу приведения сокращенной матрицы 2?2, Н =?h_i= 0;

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; вычисление НГЦФ  для  негативного узла ?(Y) = ?(54) = ?(X) +?(kl) =42 +4 = 46 и вычисление НГЦФ  для  позитивного узла ?(Y) = ?(5,4) = ?(X) + Н =42 +0 = 42 ; формулы вычисления различаются, оценки на ШАГе 2 уже не совпадают, сравнение оценок показывает, что они в этой ситуации не равны. Как поступить, какой узел выбрать ? Мы формируем маршрут Т, то включаем в него позитивную вершину (5, 4), с меньшей НГЦФ T = {(3, 5)(5, 4)(4,1)....}. Задаем соотношением экстремальности выбранному узлу (5, 4) новое имя Х = argmin{ ?(Y=(5, 4)) =46, ?(Y=(5, 4)) =42} = (5, 4) или Х = Y(k, l) = Y(5, 4).

• Сравнение текущего значения НГЦФ с исходным значением (Q*=44 )? ?(5, 4)=42 ? НЕТ.

• Вычисляется размерность матрицы и проверяется ее равенство размерности 2?2=2?2? ДА.

• В множество висячих узлов В включаем узел (Y)=(5, 4) с его оценкой НГЦФ =?(5, 4) = 46 В = {(3, 5) (4, 1) (5, 4)...}. А дальше этот ШАГ имеет отличия от предшествующих.

• Матрица С_[2] стоимостей с размером 2?2 позволяет завершить построение маршрута. Выбранными могут быть только две дуги (1, 2) весом 0 и (2, 3) весом 0 их и включаем в маршрут, завершая его. T = {(3, 5)(5, 4)(4,1)(1,2)(2, 3)} целевая функция этого маршрута определяется суммой ЦФ = 6 + 8 + 12 + 1 +15 = 42. Для других маршрутов этот реально просчитанный маршрут, а его НГЦФ = 42 может использоваться в качестве нового критерия эффективности (критерия сравнения) и основанием для выбора лучшего маршрута.

• Решение примера позволяет заменить предшествующую оценку НГЦФ Q*=44 на лучшую оценку, более реальную Q*=ЦФ = 42.

• Фрагмент дерева решений для шестого шага принимает вид:

ШАГ 7. Так как ответ на вопрос о размерности матрицы С_[4] на ШАГе 6 положительный (ДА) в алгоритме задачи происходит ряд изменений. Завершился поиск второго варианта полного маршрута с оценкой НГЦФ (Q*= ЦФ = 42), которая становится критериальной. Переходим к ответу на вопрос следует ли искать другие маршруты и окажутся ли они лучше найденного? Ответ на этот вопрос помогает указать множество В отложенных решений с оценками НГЦФ и запомненными состояниями процессов обработки. Если среди отложенных имеется оценка меньшая найденной Q*= 42, то возможно, продолжая расчет по этой ветви дерева, в итоге получим другой (третий) маршрут, лучше уже двух найденных, а при анализе всех отложенных решений (с меньшей оценкой ЦФ) будет найден оптимальный (неулучшаемый) маршрут. Действуем дальше так. В множестве В имеется оценка w = 41 < 42, которая соответствовала отказу на ШАГе 4 от выбора узла (k, l) =(3, 5) для включения в маршрут. Матрица стоимостей в той ситуации была С_[5], так как в маршрут не была включена ни одна из вершин графа путей. Мы возвращаем в матрицу дугу (3,5), но запрещаем выбор дуги С₃₅ =?, при котором в строке 3 матрицы С_[5] пропадает нулевая клетка. Ее возврат оценивается как h_i =4, для 3-й строки, что увеличивает прежнюю оценку НГЦФ. До этого уже была возвращена дуга (2,5) с запретом ее включения в маршрут назначением С₂₅ =?. Но это уже история. Остальные нули в С_[5] сохраняются. Последовательность маршрута - пуста, не содержит ни одной дуги. В третьей строке пропал нуль, поэтому ее приводим с константой h =6.

• Формируем множество S из клеток матрицы С_[5] с нулевыми значениями, определяем и вписываем в таблицу (как и ранее) значения характеристик в строках d_i и в столбцах d_j дуг- претендентов на включение в тур. Формулы обработки элементов матрицы С_[5] остаются без изменения. С

• Находим в множестве S клеток матрицы С_[5] с нулевыми значениями ту клетку, которая остальные превосходит по сумме max?_ij = 7=d_i + d_{j .}Аргументом этой суммы является клетка аrgmax?_ij = (k, l) = (3, 1);

• Преобразуем матрицу С_[5] : удаляем строку с номером k = 3 и столбец с номером l =1; при этом размерность матрицы стоимостей изменилась и стала равной (5-1)?(5-1)=4?4;

• Предотвращаем зацикливание, т.е. запрещаем выбор клетки (р, q), где q = k = 1, p = l = 3, a в позицию (l, k) = (3, 1) вписываем большое С_pq =С₃₁=? значение, делая ее запретной для выбора и включения в маршрут. Эти действия отображены в правой матрице С_[4] ниже

• Вычисляем константу приведения сокращенной матрицы 4?4, Н =?h_i= 3+0=3 ;

• Вычисляются оценки НГЦФ для позитивного и негативного узлов дерева поиска решения; вычисление НГЦФ  для  негативного узла ?(Y) = ?(3,1) = ?(X) +?(kl) =41 +7 = 48 и вычисление НГЦФ  для  позитивного узла ?(Y) = ?(3,1) = ?(X) + Н =41 +3 = 44 ; формулы вычисления различаются, оценки на ШАГе 7 не совпадают, сравнение оценок показывает, что они в этой ситуации не равны. Как поступить, какой узел выбрать ? Мы формируем маршрут Т, то включаем в него позитивную вершину (3,1), с меньшей НГЦФ T = {(3,1)…}. Задаем соотношением экстремальности выбранному узлу (3,1) новое имя Х = argmin{ ?(Y=(3,1)) =48, ?(Y=(3, 1))=44}=(3, 1) или Х = Y(k, l)=Y(3, 1).

• Сравнение текущего значения НГЦФ с исходным значением (Q*=42 )? ?(3,1)=44 ? ДА. Текущая оценка превышает исходную, следовательно, оптимальное решение уже найдено.

• Дерево решений для седьмого шага принимает вид:

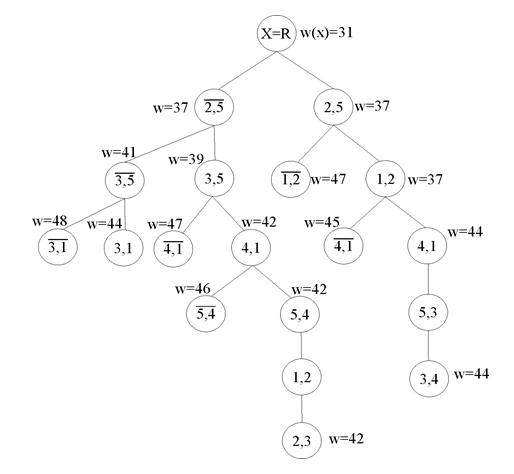
Итак, для отыскания оптимального маршрута нашего примера оказалось достаточным построить всего лишь 2 полных маршрута и найти значения целевой функции, достигаемой на маршрутах. За окончательный T^opt маршрут принимается маршрут, полученный на 6 - м шаге, T^opt = {(3, 5)(5, 4)(4,1)(1,2)(2, 3)}, ему соответствует стоимость поездок по городам ЦФ(T^opt) = 6 + 8 + 12 + 1 + 15 = 42 .