Катран, или морская собака (Squalus acanthias) – достаточно широко распространенная акула, относящаяся к роду колючих акул и семейству Катрановые акулы из отряда Катранообразные. Обитатель умеренных вод бассейнов всех мировых океанов, как правило, встречается на глубине не более 1460 метров. На сегодняшний день максимальной зарегистрированной является длина тела в пределах 160-180 см.

Эта рыбка будет хорошим примером для начала изучения пакета гидродинамического моделирования WaterLily.jl.

В этой заметке будет показано, как создать и запустить модель плывущего катрана, используя язык Julia и пакет WaterLily.jl. Этот пост адаптирован из блокнота Pluto, который вы можете скачать здесь.

using WaterLily, StaticArrays, PlutoUI, Interpolations, Plots, Images

Мы будем использовать простую модель акулы, основанную на новаторской работе Лайтхилла о плавании стройных рыб. При построении модели внимание сосредоточено на "хребте" рыбы, идеализируя форму как распределение толщины относительно оси симметрии, а движение как латеральную ("из стороны в сторону") бегущую волну. Удивительно, но этот простой подход дает представление об огромном диапазоне плавающих животных, как показано на рисунке ниже.

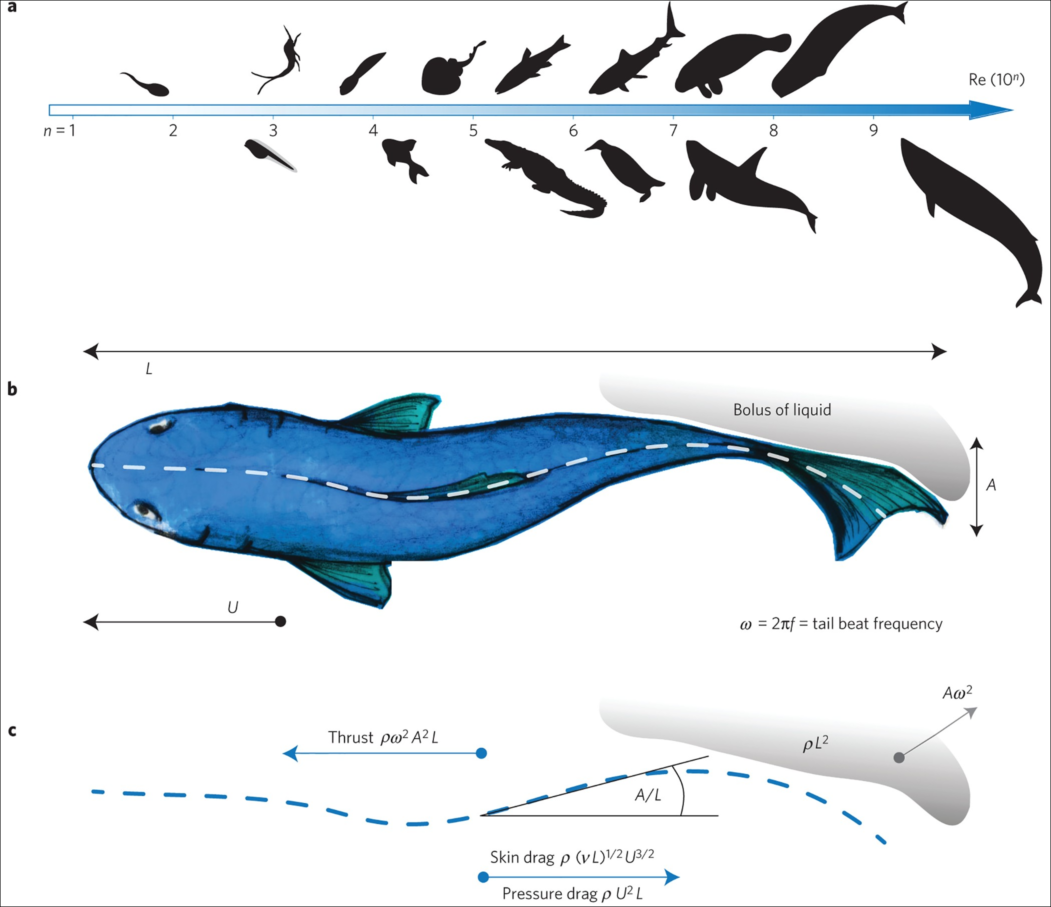
Тело и динамика

Мы определим контур тела (распределение толщины) задав несколько опорных точек и проведя интерполяцию сплайнами.

fit = y -> scale(
        interpolate(y, BSpline(Quadratic(Line(OnGrid())))),
        range(0,1,length=length(y))
    )

Скачаем картинку по которой будем создавать модель. Права на изображение принадлежат Shark Trust.

url2="https://pterosaurheresies.files.wordpress.com/2020/01/squalus-acanthias-invivo588.jpg"
filename2 = download(url2)
dogfish = load(filename2)

Чтобы задать функцию распределения толщины thk, определим ширину рыбины в нескольких местах

plot(dogfish)
nose, len = (30,224), 500
width = [0.02, 0.07, 0.06, 0.048, 0.03, 0.019, 0.01]
scatter!(
    nose[1] .+ len .* range(0, 1, length=length(width)),
    nose[2] .- len .* width, color=:blue, legend=false)
thk = fit(width)
x = 0:0.01:1
plot!(
    nose[1] .+ len .* x,
    [nose[2] .- len .* thk.(x), nose[2] .+ len .* thk.(x)],
    color=:blue)

Глядя на видеозаписи плавающих акул-собак, мы можем заметить несколько общих черт:

• Движение передней половины тела имеет небольшую амплитуду (около 20% от движения хвоста). Это задает огибающую амплитуды для бегущей волны.

envelope = [0.2,0.21,0.23,0.4,0.88,1.0]
amp = fit(envelope)

• Длина волны пробегающей по хребту рыбы немного больше длины тела

В приведенном ниже коде вы можете изменять значение λ для управления длиной бегущей волны, чтобы увидеть, какое влияние она оказывает на позвоночник в течение цикла движения.

λ = 1.4
scatter(0:0.2:1, envelope)
colors = palette(:cyclic_wrwbw_40_90_c42_n256)
for t in 1/12:1/12:1
    plot!(x, amp.(x) .* sin.(2π/λ * x .- 2π*t),
          color=colors[floor(Int,t*256)])
end
plot!(ylim=(-1.4,1.4), legend=false)

Настройка моделирования

Тело и механика движения готовы, но как мы применим их к моделированию жидкости? WaterLily использует метод погруженной границы (Метод погруженной границы для чайников) и автоматическое дифференцирование (Автоматическое дифференцирование для чайников) для внедрения тела в поток. В итоге все, что нам нужно, это функция расстояния до поверхности (SDF).

Давайте начнем с определения SDF для "позвоночника", который является отрезком прямой от 0 до 1 по х. Посмотрите замечательное видео от Inigo Quilez про вывод sdf. На графике ниже показаны sdf и нулевой контур, который ... есть просто отрезок линии.

Простые корректировки SDF дают нам контроль над формой и положением. Изменив значение y а ля y = y-shift, мы можем переместить тело вбок. А вычитая из длины контура толщину, как sdf = sdf-thickness, мы можем придать линии некоторую ширину. Это все, что нам нужно для моделирования акулы.

shift = 0.5
T = 0.5

function segment_sdf(x, y)
    s = clamp(x, 0, 1)          # distance along the segment
    y = y - shift               # shift laterally
    sdf = √sum(abs2, (x-s, y))  # line segment SDF
    return sdf - T * thk(s)     # subtract thickness
end
grid = -1:0.05:2
contourf(grid, grid, segment_sdf, clim=(-1,2), linewidth=0)
contour!(grid, grid, segment_sdf, levels=[0], color=:black)  # zero contour

После того, как проверен вид нашей SDF, мы готовы к созданию симуляции WaterLily с помощью функции fish, определенной ниже:

• В качестве аргументов принимаются функции thk для создания sdf и функция amp для создания карты бегущей волны.

• Единственным числовым параметром, передаваемым в fish, является длина рыбы L, измеряемая в расчетных ячейках. Она задает разрешение моделирования и размер массивов жидкости.

• Другими параметрами являются амплитуда для хвоста A как доля длины, число Струхаля, задающее частоту движения ω, и число Рейнольдса, задающее вязкость жидкости ν.

function fish(thk, amp, k=5.3; L=2^6, A=0.1, St=0.3, Re=1e4)
    # fraction along fish length
    s(x) = clamp(x[1]/L, 0, 1)

    # fish geometry: thickened line SDF
    sdf(x,t) = √sum(abs2, x - L * SVector(s(x), 0.)) - L * thk(s(x))

    # fish motion: travelling wave
    U = 1
    ω = 2π * St * U/(2A * L)
    function map(x, t)
        xc = x .- L # shift origin
        return xc - SVector(0., A * L * amp(s(xc)) * sin(k*s(xc)-ω*t))
    end

    # make the fish simulation
    return Simulation((4L+2,2L+2), [U,0.], L;
                        ν=U*L/Re, body=AutoBody(sdf,map))
end

# Create the swimming shark
L,A,St = 3*2^5,0.1,0.3
swimmer = fish(thk, amp; L, A, St);

# Save a time span for one swimming cycle
period = 2A/St
cycle = range(0, 23/24*period, length=24)

Мы можем проверить нашу геометрию, построив график погруженной граничной функции μ₀, которая равна 1 в жидкости и 0 внутри плавающего тела.

@gif for t ∈ cycle
    measure!(swimmer, tswimmer.L/swimmer.U)
    contour(swimmer.flow.μ₀[:,:,1]',
            aspect_ratio=:equal, legend=false, border=:none)
end

Выполнение визуализации

Анимация движения выглядит отлично, так что мы готовы запустить симулятор потока!

Функция sim_step!(sim, t, remeasure=true) запускает симулятор до момента времени t, повторно измеряя положение тела на каждом временном шаге. (по умолчанию remeasure=false, так как это требует дополнительного времени на вычисления и не нужно для статических геометрий).

# run the simulation a few cycles (this takes few seconds)
sim_step!(swimmer, 10, remeasure=true)
sim_time(swimmer)

Симуляция отработала, но по умолчанию нет никаких визуализаций или измерений.

Чтобы понять, что происходит, давайте изобразим вихри ω=curl(u) порождаемые при движении акулы. Для этого необходимо смоделировать цикл движения и вычислить завихрения во всех точках макросом @inside.

# plot the vorcity ω=curl(u) scaled by the body length L and flow speed U
function plot_vorticity(sim)
    @inside sim.flow.σ[I] = WaterLily.curl(3, I, sim.flow.u) * sim.L / sim.U
    contourf(sim.flow.σ',
             color=palette(:BuGn), clims=(-10, 10), linewidth=0,
             aspect_ratio=:equal, legend=false, border=:none)
end

# make a gif over a swimming cycle
@gif for t ∈ sim_time(swimmer) .+ cycle
    sim_step!(swimmer, t, remeasure=true)
    plot_vorticity(swimmer)
end

Красивое... (в конце концов, CFD означает Colorful Fluid Dynamics). Анимация также говорит нам кое-что важное о потоке. Обратите внимание, что от тела не отходят вихри нигде, кроме хвоста! Это признак эффективности, поскольку энергия расходуется только на создание этих вихрей.

Покопаемся еще и получим некоторые количественные измерения из моделирования. Функция ∮nds берет интеграл по поверхности тела. Зная давление p, мы можем измерить силу тяги и периферическую силу создаваемую акулой!

function get_force(sim, t)
    sim_step!(sim, t, remeasure=true)
    return WaterLily.∮nds(sim.flow.p, sim.body, t*sim.L/sim.U) ./ (0.5*sim.L*sim.U^2)
end
forces = [get_force(swimmer, t) for t ∈ sim_time(swimmer) .+ cycle]

scatter(cycle./period, [first.(forces), last.(forces)],
        labels=permutedims(["thrust", "side"]),
        xlabel="scaled time",
        ylabel="scaled force")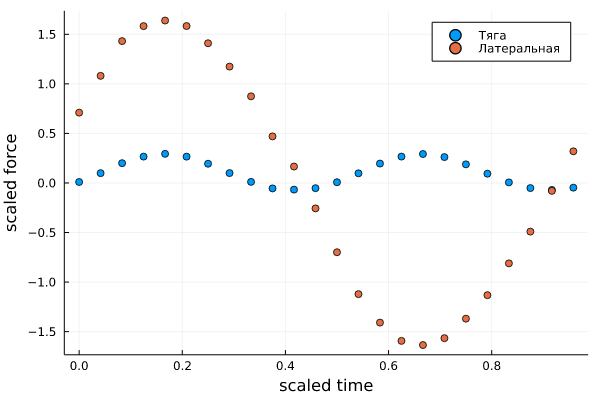

Мы можем многое узнать из этого простого графика. Например, латеральная сила (действующая из стороны в сторону) имеет ту же частоту, что и само плавательное движение, в то время как сила тяги имеет вдвое большую частоту, с пиком каждый раз, когда хвост проходит через центральную линию.

Следующие шаги

Эта простая модель - отличное начало, и она открывает тонну возможностей для улучшения симуляции акулы и предложения вопросов для исследования:

• Мгновенные силы должны быть равны нулю в свободно плавающем теле! Для этого мы можем добавить в нашу модель движения реакции. Будет ли модель акулы плыть по прямой, если мы сделаем это, или необходим цикл управления?

• Настоящие акулы куда трехмерней. Хотя мы можем легко обобщить этот подход, используя двумерные сплайны, моделирование займет гораздо больше времени. Есть ли способ использовать GPU для ускорения моделирования без полного изменения солвера?

• Если бы мы собирались сделать робота вдохновленного биомеханикой акулы, у нас были бы ограничения на форму, движение и доступное питание. Можем ли мы использовать эту структуру для оптимизации нашей робототехники в рамках имеющихся ограничений?

Ниже приведены ссылки на все пакеты, используемые в этом блокноте. Счастливого моделирования!

1. Interpolations.jl

2. JuliaDiff

3. JuliaImages

4. Plots.jl

5. Pluto.jl и PlutoUI.jl

6. StaticArrays.jl

7. WaterLily.jl