
Задача состоит в классификации гидроакустических сигналов. Сонары (гидролокаторы) посылают звук высокой частоты в определенном направлении и получают отраженную звуковую волну. По характеристике этой волны можно сделать вывод, от чего именно она отразилась – от морской мины или же от подводного камня, скалы. Используемый для решения задачи набор данных был разработан сотрудником аэрокосмического технологического центра Полом Горманом в разгар холодной войны. Для получения данных металлический цилиндр и цилиндрическая горная порода, оба длиной около 1,5 метров, размещались на песчаном дне океана.
База данных о гидроакустических сигналах содержит 208 экземпляров и 60 атрибутов. Файл «sonar.mines» содержит 111 экземпляров, полученных путем отскакивания сигналов от мины под разными углами и при различных условиях. Файл «sonar.rocks» содержит 97 экземпляров, полученных от камней или скал в аналогичных условиях. Переданный сигнал гидролокатора представляет собой частотно-модулированный ЛЧМ, повышающийся по частоте. Каждый экземпляр представляет собой набор из 60 чисел в диапазоне от 0,0 до 1,0. Каждое число представляет энергию в пределах определенной полосы частот, полученной за определенный период времени. Метка, связанная с каждой записью, содержит букву «R», если объект представляет собой камень/скалу («Rocks»), и «M», если это мина («Mines»). Оба файла с представлением данных были интегрированы в один csv-файл «sonar.all-data.csv».
Текущая работа посвящена сравнению различных классификаторов машинного обучения на описанном наборе данных. Среди таких классификаторов были выбраны многослойный персептрон, решающее дерево (деревья решений), случайный лес, логистическая регрессия и метод k ближайших соседей. Для создания классификаторов использовалась Python-библиотека Scikit-Learn. Набор данных уже нормализован. Следовательно, единственная предварительная обработка, которую здесь необходимо выполнить, состоит в том, чтобы разбить набор данных на атрибуты и метки классов (листинг 1), а затем разделить его на данные для обучения и тестирования. Так, использование разбиения 20:80 для тестирования и обучения оставляет 166 экземпляров для обучения (и проверки), а также 42 экземпляра для окончательной оценки. После этого можно применить различные алгоритмы классификации для получения окончательного результата.
Листинг 1. Исходный код функции разбиения данных для обучения модели
def PrepareData():
dataset = dataframe.values # получить данные в виде numpy-массива
X = dataset[:,0:60].astype(float) # вещественные данные
Y = dataset[:,60] # метки R и M
return X, Y # вернуть атрибуты и метки классов в виде двух массивовПо нажатию кнопки «Результат выбранной модели» программа выводит на экран результаты и точность прогноза модели выбранного в раскрывающемся списке классификатора. Для этого вызывается соответствующая ему функция (на примере многослойного персептрона – см. рисунок 1 и листинг 2), в которой выполняется построение модели, ее обучение и тестирование (листинг 3).
Листинг 2. Исходный код функции для обучения и тестирования модели многослойного персептрона
def MLP():
T.delete(1.0, tk.END) # очистить текстовое поле
X, Y = PrepareData() # разбить полученные данные
# Настройка модели многослойного перспетрона с тремя слоями по 100, 30 и 10 нейронов на каждом:
mlp = MLPClassifier(hidden_layer_sizes=(100, 30, 10),
tol=0.001, learning_rate_init=0.001, random_state=99)
# начальная скорость модели learning_rate_init и оптимизационный допуск tol подбираются экспериментально
s = 'Многослойный персептрон: \n\n'
s += GetScore(X, Y, mlp) # получить результаты обучения и тестирования и записать их в конец строки s
T.insert(tk.END, s) # вставить в текстовое поле строку s с результатом
def DT(): # функция для обучения и тестирования модели решающего дерева
T.delete(1.0, tk.END) # очистить текстовое поле
X, Y = PrepareData() # разбить полученные данные
# Настройка модели дерева принятия решений: энтропия в качестве критерия классификации и неограниченная глубина дерева
dtc = DecisionTreeClassifier(criterion='entropy',
max_features='auto',
max_depth=None,
random_state=99
)
s = 'Решающее дерево: \n\n'
s += GetScore(X, Y, dtc) # получить результаты обучения и тестирования и записать их в конец строки s
T.insert(tk.END, s) # вставить в текстовое поле строку s с результатомЛистинг 3. Исходный код функции для обучения и тестирования модели model на данных X, Y
def GetScore(X, Y, model):
accuracy = 0 # точность распознавания
correct = 0 # верно распознанных ответов
total = 0 # всего ответов
i = 0 # номер экземпляра
# разбиение исходных данных X, Y на обучающую выборку (X_train, Y_train) и тестовую (X_validation, Y_validation)
# в соотношении 80:20. random_state отличный от None нужен для случайных, но воспроизводимых наборов данных
X_train, X_validation, Y_train, Y_validation = train_test_split(X, Y, test_size=0.20, random_state=99)
model.fit(X_train, Y_train) # обучение модели
s = '' # строка с выводом результатов
for row in X_validation: # для каждой строки данных в тестовом наборе
guess = model.predict(row.reshape(1, -1)) # предсказание на строке, записанной в виде матрицы из одного столбца
s += str(i + 1) + ') Предсказано: ' + guess[0] + '; Верно: ' + str(Y_validation[i]) + '\n' # вывод результата предсказания и верной метки
if guess[0] == Y_validation[i]: # если эти значения совпали, то
correct += 1 # увеличить количество верно распознанных ответов
i += 1
total += 1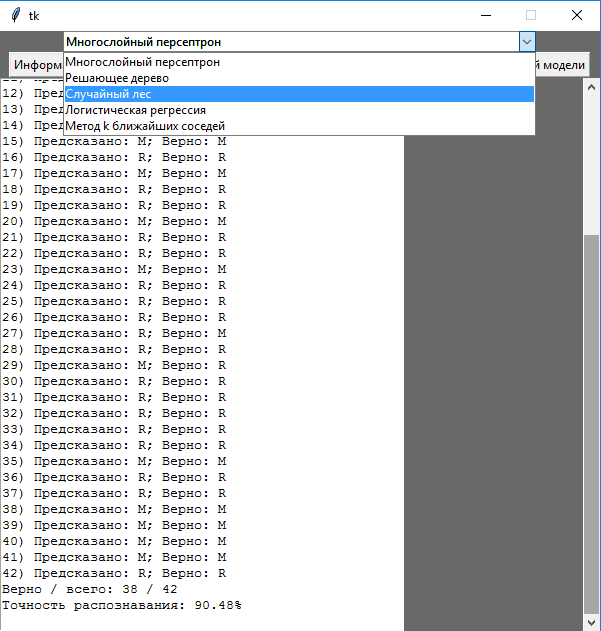
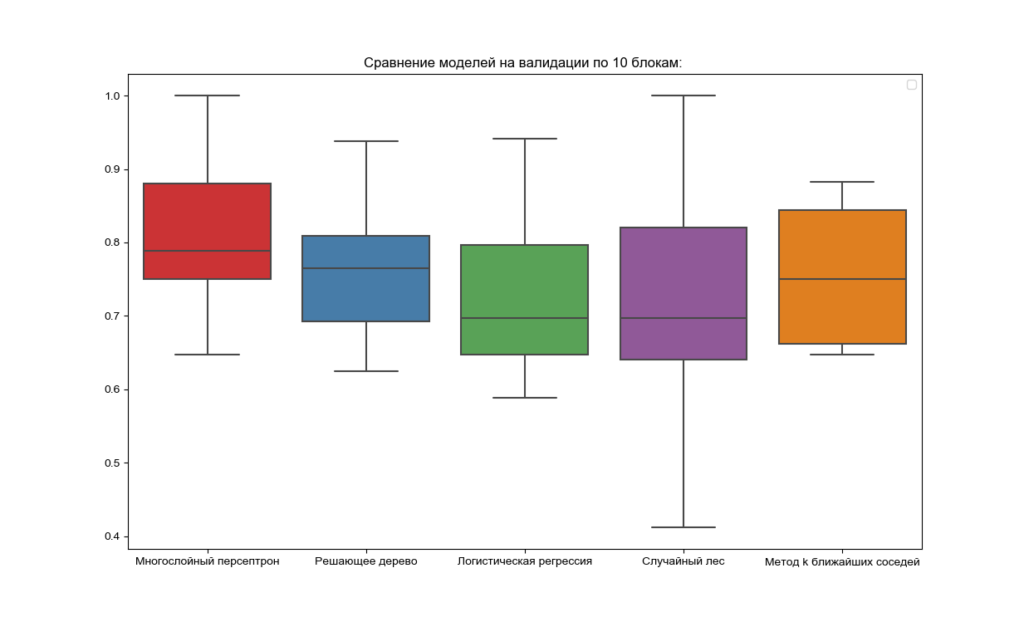
Также в программе предусмотрено построение графиков точности распознавания по каждой модели и построение диаграмм размаха (так называемых «ящиков с усами»), позволяющих оценить медианные значения точности всех используемых классификаторов (см. листинг 4 и рисунок 2). Таким образом, по результатам перекрестной проверки с разделением используемого набора данных по 10 блоков модель многослойного персептрона демонстрирует максимальную точность.
Листинг 4. Исходный код функции построения графиков всех моделей
def DrawPlot():
models = [] # список моделей
X, Y = PrepareData() # разбить полученные данные
# разбиение исходных данных X, Y на обучающую выборку (X_train, Y_train) и тестовую (X_validation, Y_validation)
# в соотношении 80:20. random_state отличный от None нужен для случайных, но воспроизводимых наборов данных
X_train, X_validation, Y_train, Y_validation = train_test_split(X, Y, test_size=0.20, random_state=99)
# добавление всех моделей в список:
models.append(('Многослойный персептрон', MLPClassifier(hidden_layer_sizes=(1000, 30, 10),
tol=0.001,
learning_rate_init=0.001,
random_state=99)))
models.append(('Решающее дерево', DecisionTreeClassifier(criterion='entropy',
max_features='auto',
max_depth=None,
random_state=99
)))
models.append(('Логистическая регрессия', LogisticRegression()))
models.append(('Случайный лес', RandomForestClassifier(n_estimators=10, criterion='entropy', max_features='auto', max_depth=None, random_state=99)))
models.append(('Метод k ближайших соседей', KNeighborsClassifier()))
results = [] # список результатов
names = [] # список названий моделей
scoring = 'accuracy' # выбранная метрика - точность распознавания
s = 'Сравнение моделей на валидации по 10 блокам: \n\n'
for name, model in models: # цикл по всем моделям списка
# кросс-валидация на 10 частях исходного набора данных
kfold = KFold(n_splits=10)
# обучение модели на на 10 частях с получением результата (оценки распознавания)
cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)
results.append(cv_results) # добавить результаты в список результатов
names.append(name) # добавить название модели в список названий моделей
s += name + ': ' + str(round(cv_results.mean() * 100, 2)) + '%\n' # вывести в строку среднее по всем разбиениям в виде процентов с округлением до двух знаков после запятой
T.insert(tk.END, s) # вставить в текстовое поле строку s с результатом
plt.figure(figsize=(15, 10)) # создание фигуры с заданными размерами
plt.title('Сравнение моделей на валидации по 10 блокам: ') # создание заголовка графика
sns.set_style(style='whitegrid')
initial = sns.boxplot(data=results, palette='Set1', notch=False) # построение графиков по данным
initial.set_xticklabels(['Многослойный персептрон', 'Решающее дерево', 'Логистическая регрессия', 'Случайный лес','Метод k ближайших соседей']) # вывод подписей
initial.legend()
plt.show() # показать графикБлагодаря быстрому развитию науки и технологий, автоматическое распознавание объектов было реализовано за короткое время. Однако у традиционных методов есть множество недостатков, которые необходимо устранить. Из-за природы подводного мира процедура сбора и обработки данных более ограничена, чем на суше (или в воздухе), поэтому существует несколько проблем при использовании более агрессивных и открытых методов. По этой причине наиболее уместным видится сочетание традиционных методов исследования с методами машинного обучения, которые позволяют значительно снизить количество ложных срабатываний.
Таким образом, в рамках работы была решена задача бинарной классификации сигналов: отклику классификатора 1 соответствует метка «M» (mines – мина), 0 – «R» (rocks – камень, скала). Итогом стало сравнение точности различных классификаторов машинного обучения на наборе данных «Sonar, Mines and Rocks». Благодаря выполненной работе будущим исследователям будет легче проанализировать существующие методы, извлечь необходимые уроки и разработать эффективную модель для преодоления существующих недостатков.
Следует отметить, что задачи подобного класса часто решаются в аудите. Одним из примеров может служить расчет аудиторского риска по имеющимся данным финансовой отчетности фирм в различных секторах. В ходе планирования аудита изучаются существующие и исторические факторы риска. Предназначенный для решения задачи классификатор (например, модель глубокого обучения) позволяет получить соответствующий отклик: единице соответствует метка «мошенническая фирма», 0 – «не мошенническая фирма». Другой пример – промышленный аудит внутри конкретной компании. Например, в сфере медицины аудит качества доступности лекарственных средств (0 – «лекарство недоступно», 1 – «доступно») имеет дело с данными по их лабораторным исследованиям, сроку годности, доставке в больницы и т.п. Чтобы ускорить автоматизацию аудита в эпоху больших данных, для решения этой задачи могут быть использованы различные ансамблевые модели, сочетающие два и более классификаторов машинного обучения.

