Применение алгоритма Гровера для поиска гамильтоновых циклов в графе / forpes.ru

Главная
Применение алгоритма Гровера для поиска гамильтоновых циклов в графе

Применение алгоритма Гровера для поиска гамильтоновых циклов в графе +21

03.11.2021 14:07

nkochelev 4 2300 Источник

1. Введение

В данной статье представлен вариант применения квантового алгоритма Гровера для решения задачи поиска гамильтоновых циклов в графе.

Сразу отмечу, что данный вариант решения задачи является учебным. Он не даст так называемого «квантового превосходства», поскольку при росте числа вершин в графе, нам потребуется большее число кубит, циклов Гровера и запусков самого алгоритма. Однако, считаю, что данный вариант заслуживает внимания, возможно он вдохновит кого-либо на поиск более оптимального решения.

2. Постановка задачи

Представим, что существует граф, состоящий из пяти вершин O, A, B, C, D, и восьми ребер. Вершину O мы будем считать исходной точкой.

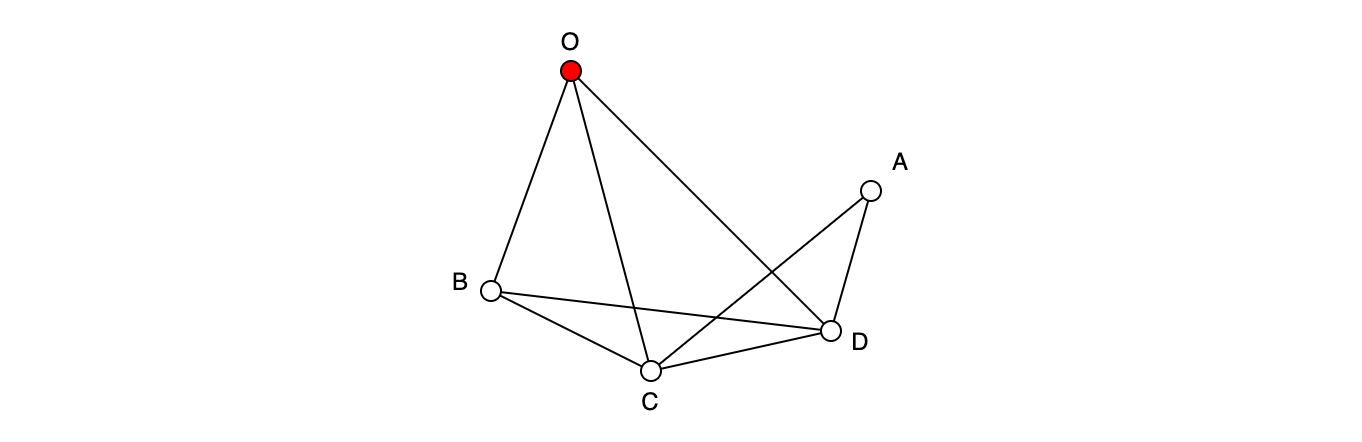
Некий путник, который находится в точке O, хочет пройти через все вершины графа, зайти в каждую из них только один раз и вернуться снова в исходную точку O. Необходимо найти все возможные маршруты путника, удовлетворяющие условиям задачи.

Решение этой задачи легко найти самостоятельно. Всего существуют 4 варианта такого пути, при том, что два из них являются обратными последовательностями двух других:

OCADBO и OBDACO

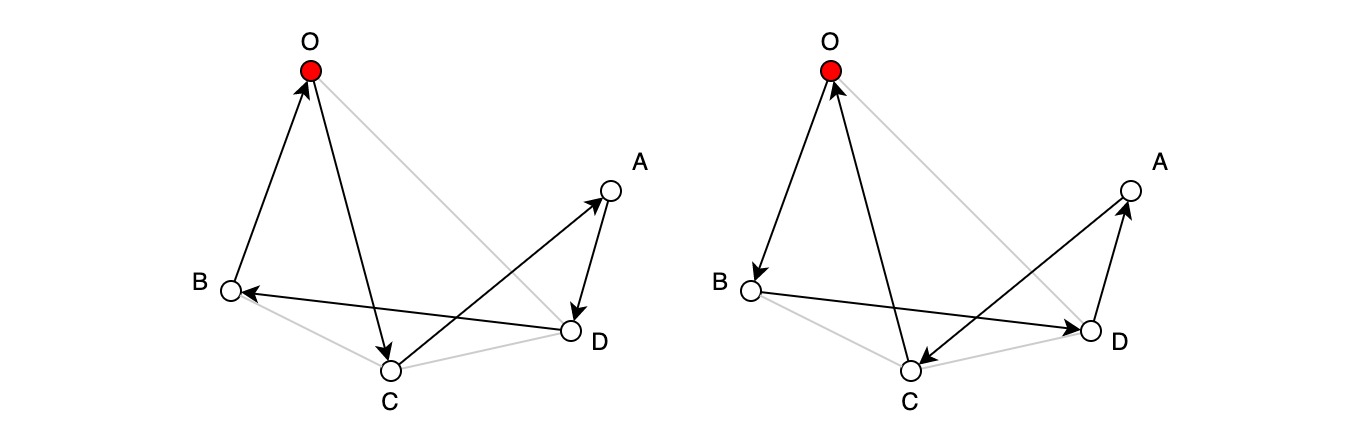
ODACBO и OBCADO

Путнику, находящемуся в исходной точке O, необходимо совершить 5 шагов. На каждом из шагов путник переходит по связывающему ребру из одной вершины в другую. Все посещенные вершины должны быть уникальны для маршрута, кроме точки O, в ней путник оказывается дважды, поскольку последний 5-ый шаг должен привести его на исходную позицию.

Маршрутом мы будем называть последовательность вершин, через которые должен пройти путник, например: OBCADO. Каким бы ни был маршрут (последовательность вершин), он должна удовлетворять следующим правилам:

вершины маршрута должны быть уникальны, путник дважды не заходит в один и тот же пункт;
переход на любом шаге маршрута возможен только в ту вершину, которая связана с текущей:
- A соединяется с C и D
- B соединяется с O, C и D
- C соединяется с O, A, B, C, D
- D соединяется с O, A, B, C, D
маршрут начинается и заканчивается в точке O, поэтому для простоты мы исключим ее из маршрута, оставим только изменяющуюся часть — 4 вершины.

Как будем решать?

Решить данную задачу можно в лоб, методом перебора. Итак, мы будем перебирать 4 * 4 * 4 * 4 = 256 комбинации вершин:

$AAAA, AAAB, AAAC, AAAD, AABA, AABB, \dots, DDDD$

При переборе нам необходимо определить, удовлетворяет ли рассматриваемый в конкретный момент маршрут условиям задачи. Рассмотрим несколько примеров.

Допустим, мы рассматриваем маршрут ADCB. Он невозможен для путника, поскольку первый шаг должен быть из точки O в одну из вершин, соединенных с этой точкой. Вершина A не соединяется с точкой O, такой маршрут мы должны отбросить.

Другой пример, маршрут CAAB — его также необходимо отбросить, поскольку в нем путнику придется дважды зайти в вершину A.

Еще пример, маршрут BACD, тоже отбрасываем, путник никак не может попасть из вершины B сразу в вершину A (второй шаг), так как эти вершины не связаны.

Итак, нам необходимо перебрать 256 комбинаций, из которых следует отбрасывать те, в которых:

повторяется хотя бы одна из вершин
любые две соседние вершины в комбинации не связаны ребром
первая в комбинации вершина не связана с исходной точкой O
последняя в комбинации вершина не связана с исходной точкой O

Решить данную задачу можно в цикле на обычном ПК, однако, мы преследуем учебные цели и хотим разработать решение для квантового компьютера. Для этого будем использовать квантовый алгоритм Гровера.

Выразим маршрут и вершины на языке кубит.

Возьмем 8 кубит, разобьем их условно на 4 пары. Первая пара соответствует первой вершине пути, вторая пара — второй вершине, и т.д. В каждой паре кубит возможна одна из 4-х комбинаций кубит: 00, 01, 10, 11. Положим, что каждой из этих комбинаций соответствует одна из возможных вершин: A, B, C, D:

$A = 00, \ B = 01, \ C = 10,\ D = 11$

Рассмотренные ранее комбинации ADCB, CAAB и BACD будут соответствовать следующим комбинациям кубит: 00111001, 10000001 и 01001011 соответственно.

Если мы применим к этим восьми кубитам оператор Адамара, то получим суперпозицию из всех возможных вариантов движения путника, то есть все 256 комбинаций. Далее в оракуле нам необходимо реализовать процедуры, которые будут проверять эти комбинации на соответствие условиям задачи.

Однако, еще до реализации оракула мы можем воспользоваться одной хитростью, которая позволит нам сократить число комбинаций почти в два раза.

3. Суперпозиция

Самым первым шагом большинства квантовых алгоритмов является создание суперпозиции всех входных кубитов. Однако, мы можем тут отойти от традиции и применить небольшую хитрость, которую применили авторы этой статьи. Суть хитрости заключается в следующем: если нам известны невозможные комбинации кубит, мы можем их заранее исключить из суперпозиции.

Поскольку 1-ый шаг совершается из точки O, и первая вершина должна быть связана с этой точкой, значит это не может быть вершина A, это могут быть только вершины B, C или D. Аналогично, последний 5-ый шаг совершается из 4-ой вершины в точку O, и она должна быть связана с точкой O, значит это не может быть вершина A.

Раз первая вершина в маршруте может быть только вершиной B, C или D, то и первая пара кубит, соответствующая первой вершине в маршруте путника, может принимать только следующие значения: 01, 10 и 11. Это же справедливо и для последней пары кубит, соответствующей четвертой вершине маршрута.

Таким образом, мы исключим из суперпозиции ненужную комбинацию 00 (вершину A) для первой и четвертой вершины и, благодаря этому нам уже не потребуется в оракуле проводить проверку на связь этих вершин с точкой O, и мы сократим число комбинаций до 3 * 4 * 4 * 3 = 144.

Итак, рассмотрим, как работает этот прием для пары кубит.

Начальное состояние системы из двух кубит запишем следующим образом:

$| \psi_0 \rangle = | {0} \rangle \otimes | 0 \rangle$

Выполним ряд преобразований.

Шаг 1. Подействуем на первый кубит оператором

$R_y = \begin{pmatrix} \cos{\tfrac{\theta}{2}} & - \sin{\tfrac{\theta}{2}} \\ \sin{\tfrac{\theta}{2}} & \cos{\tfrac{\theta}{2}} \end{pmatrix}$

с таким углом $\theta$ , при котором матрица оператора принимает следующий вид:

$\begin{pmatrix} \tfrac{1}{\sqrt{3}} & \sqrt{\tfrac{2}{3}} \\ \sqrt{\tfrac{2}{3}} & \tfrac{1}{\sqrt{3}} \end{pmatrix}$

Не будем для угла $\theta$ искать «красивое» значение, положим его равным:

$\theta = 2 \cdot \arccos{\tfrac{1}{\sqrt{3}}}$

Посмотрим, как этот оператор подействует на первый кубит $| 0 \rangle$ :

$R_y | 0 \rangle = \begin{pmatrix} \tfrac{1}{\sqrt{3}} & \sqrt{\tfrac{2}{3}} \\ \sqrt{\tfrac{2}{3}} & \tfrac{1}{\sqrt{3}} \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} \tfrac{1}{\sqrt{3}} \\ \sqrt{\tfrac{2}{3}} \end{pmatrix} = \tfrac{1}{\sqrt{3}} | 0 \rangle + \sqrt{\tfrac{2}{3}} | 1 \rangle$

После действия оператора на первый кубит пары мы получим следующую суперпозицию 2-х кубит:

$| \psi_1 \rangle = \left ( \tfrac{1}{\sqrt{3}} | 0 \rangle + \sqrt{\tfrac{2}{3}} | 1 \rangle \right ) \otimes | 0 \rangle = \tfrac{1}{\sqrt{3}} | 00 \rangle + \sqrt{\tfrac{2}{3}} | 10 \rangle$

Шаг 2. Подействуем на второй кубит контролируемым вентилем Адамара

Контролируемый вентиль Адамара изменяет второй кубит только тогда, когда первый кубит равен $| 1 \rangle$

$| \psi_2 \rangle = \tfrac{1}{\sqrt{3}} | 00 \rangle + \sqrt{\tfrac{2}{3}} | 1 \rangle \otimes H | 0 \rangle = \tfrac{1}{\sqrt{3}} | 00 \rangle + \sqrt{\tfrac{2}{3}} | 1 \rangle \otimes \left ( \tfrac{1}{\sqrt{2}} | 0 \rangle + \tfrac{1}{\sqrt{2}} | 1 \rangle \right ) = \\ =\ \tfrac{1}{\sqrt{3}} | 00 \rangle + \tfrac{1}{\sqrt{3}}| 10 \rangle + \tfrac{1}{\sqrt{3}} | 11 \rangle$

Шаг 3. Подействуем на второй кубит вентилем NOT

Ко второму кубиту применим вентиль NOT:

$| \psi_3 \rangle = \tfrac{1}{\sqrt{3}} | 0 \rangle \otimes X | 0 \rangle + \tfrac{1}{\sqrt{3}} | 1 \rangle \otimes X | 0 \rangle + \tfrac{1}{\sqrt{3}} | 1 \rangle \otimes X | 1 \rangle = \\ =\ \tfrac{1}{\sqrt{3}} | 01 \rangle + \tfrac{1}{\sqrt{3}} | 11 \rangle + \tfrac{1}{\sqrt{3}} | 10 \rangle$

Итак, мы получили суперпозицию, в которой отсутствует комбинация 00.

После того, как мы подробно разобрали теоретическую часть, приступим к написанию соответствующей процедуры. Библиотека qiskit имеет в своем арсенале все вентили, приведенные в теоретической части:

Однокубитный вентиль — QuantumCirquit.ry(theta, target_qubit)
- theta — угол $\theta$
- target_qubit — кубит, на который воздействует вентиль
Контролируемый вентиль Адамара — QuantumCirquit.ch(control_qubit, target_qubit)
- control_qubit — контролирующий кубит
- target_qubit — кубит, на который воздействует вентиль
Однокубитный вентиль NOT— QuantumCirquit.x(target_qubit)
- target_qubit — кубит, на который воздействует вентиль

Напишем процедуру, которая на вход будет получать пару кубит и применять к ним последовательно все перечисленные в теоретической части операторы:

import numpy as np

theta = 2 * np.arccos(1 / np.sqrt(3))

def exclude_00(qc, pair, reverse=False):

    if not reverse:
        qc.ry(theta, pair[0])
        qc.ch(pair[0], pair[1])
        qc.x(pair[1])
    else:
        qc.x(pair[1])
        qc.ch(pair[0], pair[1])
        qc.ry(-theta, pair[0])

Отмечу сразу, должна быть возможность выполнить данную процедуру в обратном порядке, поэтому мы ввели дополнительный аргумент reverse. О необходимости в этом подробнее расскажу позже.

Исключать возможность получить вариант A мы будем из первой и четвертой вершины маршрута. Вторая и третья вершины должны иметь все возможные варианты в суперпозиции, поэтому на них будем действовать классически — вентилем Адамара.

4. Оракул

В алгоритме Гровера оракул должен инвертировать фазу «хорошей» комбинации входящих кубит. Если комбинация удовлетворяет условиям уникальности и требованию по связанности вершин, то у такой комбинации оракул должен изменить фазу. В противном случае, если хотя бы одно из условий будет нарушено, оракул оставляет фазу неизменной.

Инверсия фазы равносильна простой инверсии результирующего кубита из $| 1 \rangle$ в $| 0 \rangle$ , который не является частью входных кубит маршрута. Оракул должен быть построен таким образом, чтобы для «хорошей» комбинации результирующий кубит изменял свое состояние $| 1 \rangle$ на состояние $| 0 \rangle$ .

По умолчанию комбинация объявляется «хорошей». Однако, если будет найдено хотя бы одного совпадение вершин или один несвязанный переход между ними, маршрут будет признан «плохим» и инверсии результирующего кубита не произойдет.

На рисунке условно изображена схема алгоритма для решения нашей задачи.

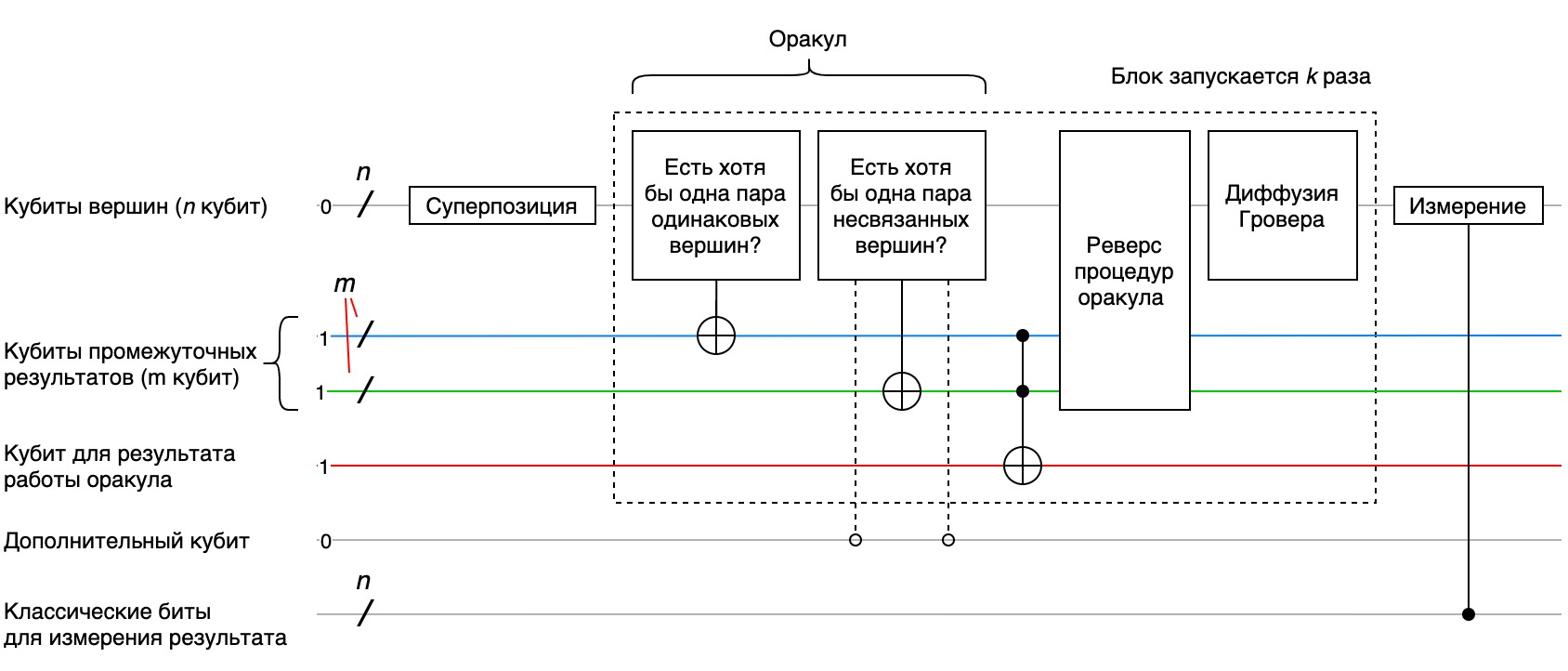
Рассмотрим детально содержание проверок на уникальность и на связанность вершин.

4.1. Контроль совпадения вершин

Задача данного блока состоит в том, чтобы не дать оракулу инвертировать результирующий кубит, если вдруг в комбинации встретятся хотя бы две одинаковых вершины.

Чтобы проверить, нет ли совпадающих вершин в комбинации, нам необходимо последовательно проверить все возможные пары вершин на равенство. Для каждой пары вершин будем проверять, не являются ли они обе одновременно либо вершинами A, либо B, либо C, либо D.

Представим, что на вход подаются две вершины A, тогда все четыре входных кубита равны 0. После применения ко всем четырем кубитам вентиля NOT они становятся равны 1. Множественный вентиль Тоффоли инвертирует результирующий кубит. Дальше в схеме кубиты будут подвержены преобразованию для проверки одновременного равенства вершинам B, C и D. Эти проверки будут неудачными и не изменят результирующий кубит, его значение останется инвертированным.

Если на вход подаются несовпадающие вершины, результирующий кубит на всех этапах схемы останется нетронутым.

Процедура проверки совпадения вершин

Напишем простую процедуру, на вход которой будем подавать две пары кубит, соответствующие двум вершинам маршрута, а также кубит, в который функция будет передавать результат проверки.

Eсли в качестве пар переданы одинаковые вершины, то процедура изменяет результирующий кубит на обратный, сигнализирует о совпадение вершин.

def find_equality(qc, pair_1, pair_2, result_qubit):

    qc.x(pair_1 + pair_2)
    qc.mct(pair_1 + pair_2, result_qubit)

    qc.x([pair_1[1], pair_2[1]])
    qc.mct(pair_1 + pair_2, result_qubit)

    qc.x(pair_1 + pair_2)
    qc.mct(pair_1 + pair_2, result_qubit)

    qc.x([pair_1[1], pair_2[1]])
    qc.mct(pair_1 + pair_2, result_qubit)

Полная схема «детектора совпадений» будет выглядеть примерно так:

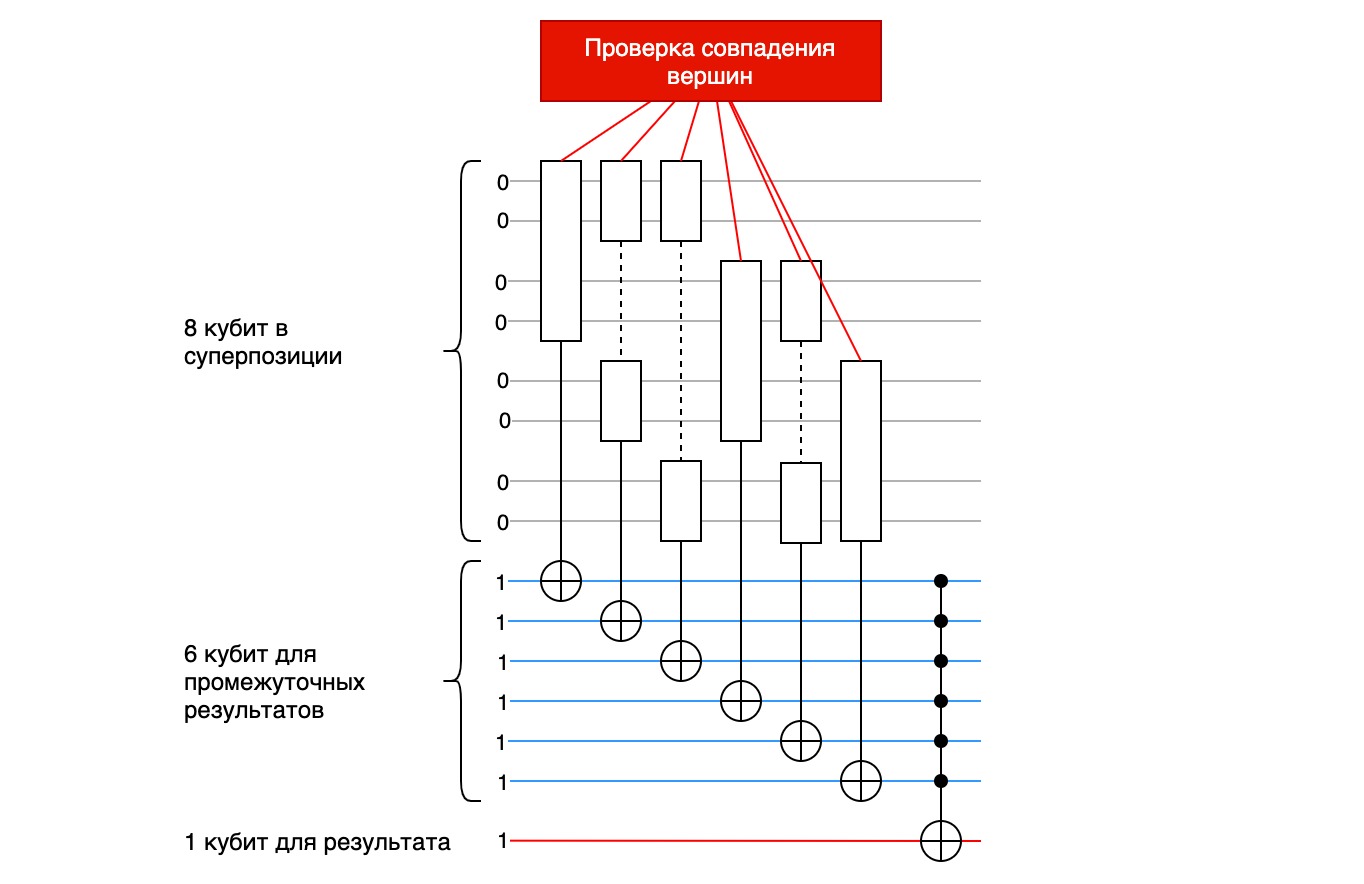
В оракуле нам потребуется применить эту процедуру ко всем парам вершин, а поскольку у нас 4 вершины, то процедуру придется запустить 6 раз — это число сочетаний из 4-х по 2:

$C_n^k=\frac{n!}{k!\left(n-k\right)!} = \frac{4!}{2!\cdot 2!} = 6$

При восьми вершинах нам уже потребуется запустить данную функцию для 28 пар вершин. Именно эта часть алгоритма и является узким местом.

4.2. Проверка связи вершин

Задача данного блока оракула состоит в том, чтобы для всех трех пар рядом стоящих вершин определить, существует ли связывающее их ребро. Если хотя бы у одной такой пары нет связи, то процедура не позволяет оракулу, объявить комбинацию «хорошей» и изменить результирующий кубит. Изменив результирующий кубит на 0, процедура не даст оракулу объявить такой маршрут «хорошим».

Суммарная логика должна быть такая: результирующий кубит проверки на связанность вершин должен измениться (1 → 0) если хотя бы одна пара рядом стоящих вершин не будет связана ребром.

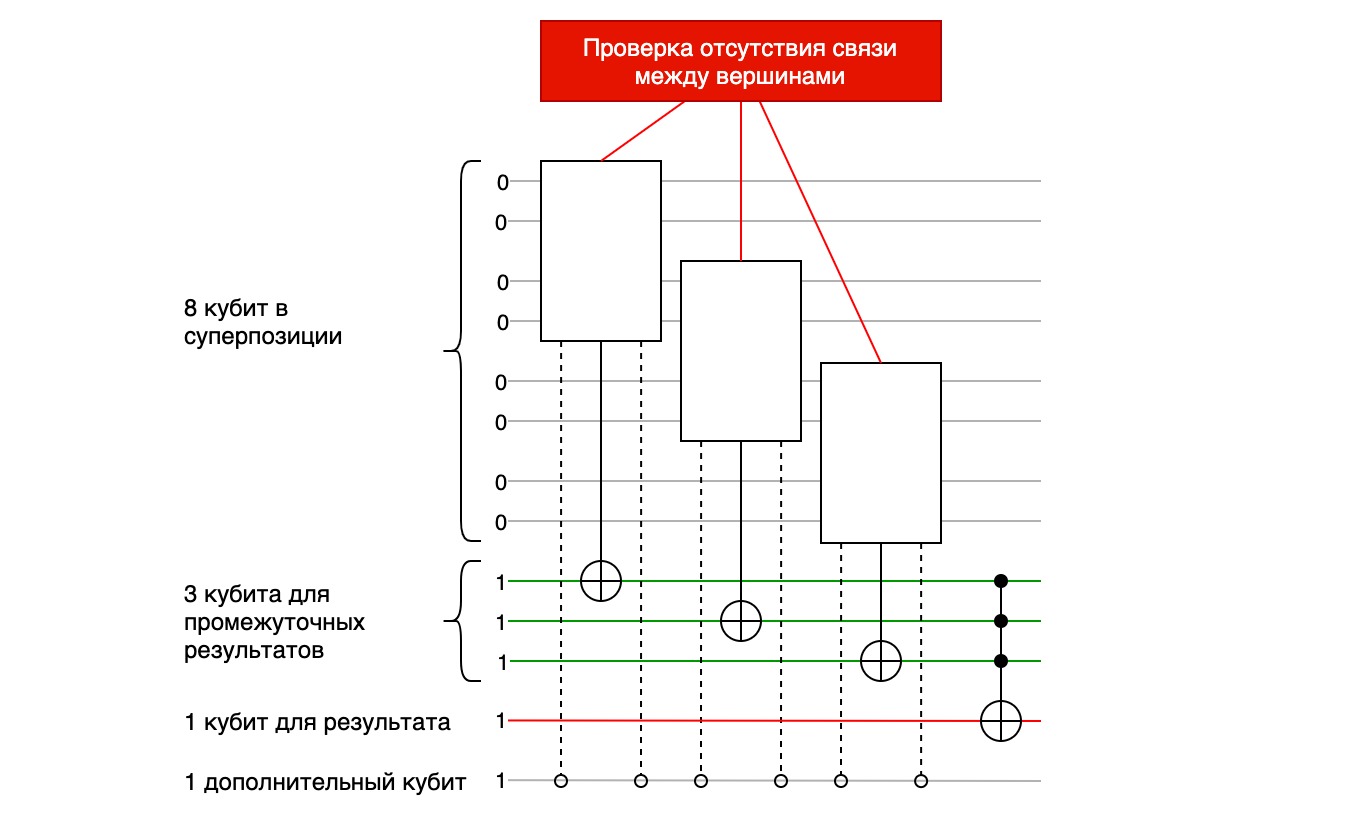
Как мы будем решать эту задачу?

Допустим мы проверяем 3-ю и 4-ю вершины маршрута. И допустим, 3-я вершина есть вершина A. Но мы знаем, что из вершины A можно попасть только в вершины C и D. Следовательно, сначала нужно проверить, выпала ли на 3-ем шаге вершина A, и если это так, то проверить, какая вершина следующая. Нам необходимо выявить именно негативные случаи, когда следующая 4-ая вершина не является ни вершиной C, ни D, и только в этом случае объявить комбинацию неудачной. Проверить это мы сможем от обратного, если 4-ая вершина является вершиной A или B (логически эквивалентно «ни C, ни D»), то считаем текущую комбинацию неудачной. Такая «обратная» форма для нас проще в реализации и позволит сократить число дополнительных кубит.

Не забываем про то, что нам необходимо провести аналогичные проверки для всех остальных случаев, когда третья вершина есть B, C или D. А также для всех возможных пар рядом стоящих вершин в маршруте.

Приступим к реализации данной процедуры. На вход ей будем подавать один кубит для результата и две пары кубит двух вершин. Первую будем называть основной, вторую — соседней.

Мы будем последовательно проверять, какой вершиной (A, B, C или D) является основная вершина. Для этого нам потребуется вентиль Тоффоли. Далее для каждой из возможных ситуаций будем проверять соседнюю вершину на предмет того, является ли она связанной с основной вершиной.

Логика работы процедуры следующая:

Проверяем, является ли основная вершина вершиной A, если верно, то проверяем:
- Является ли соседняя вершина вершиной A или B, если верно, то инвертируем результирующий кубит.
Проверяем, является ли основная вершина вершиной B, если верно, то проверяем:
- Является ли соседняя вершина вершиной A или B, если верно, то инвертируем результирующий кубит.
Проверяем, является ли основная вершина вершиной C, если верно, то проверяем:
- Является ли соседняя вершина любой, то инвертируем результирующий кубит (условие всегда выполняется).
Проверяем, является ли основная вершина вершиной D, если верно, то далее логика аналогична логике с вершиной C.

Давайте детально рассмотрим алгоритм описанных выше проверок.

Сначала проверяем, является ли основная вершина вершиной A.

Но каким образом мы можем это проверить? Вершина A в виде кубит имеет представление 00, мы можем к обоим кубитам применить вентиль NOT, тогда пара станет равной 11. Далее мы направляем эту пару в вентиль Тоффоли в качестве контролирующих кубит, он инвертирует дополнительный кубит (0 → 1). Если основная вершина не является вершиной A, то дополнительный кубит останется неизменным. Если же равна — то дополнительный кубит будет инвертированным.

Далее, нам необходимо проверить соседнюю вершину на предмет равенства вершине A или B. Для этого мы вводим дополнительный кубит для сохранения промежуточного результата проверки, применяем множественный вентиль Тоффоли к двум кубитам проверяемой вершины, но также в качестве контрольного кубита подаем в вентиль дополнительный кубит с результатом проверки на равенство основной вершины вершине A. В случае успеха вентиль Тоффоли инвертирует кубит промежуточного результата проверки.

С теоретической частью закончили, приступаем к написанию процедуры.

Сначала составим общий список вершин, заодно зафиксируем для вершин представления в кубитах:

vertex_names = {
    'A': '00',
    'B': '01',
    'C': '10',
    'D': '11',
}

Зафиксируем все связи вершин (кроме точки O).

connections = {
    'A': ['C','D'],
    'B': ['C','D'],
    'C': ['A','B','D'],
    'D': ['A','B','C'],
}

Создадим справочник функций, который при подаче на вход вершины, соответствующей ключу в словаре, на выходе выдаст пару кубит 11. Вместе с вентилем Тоффоли этот справочник можно использовать как условный оператор.

vertex_to_11 = {
    'A': lambda qc, pair: qc.x(pair),
    'B': lambda qc, pair: qc.x(pair[0]),
    'C': lambda qc, pair: qc.x(pair[1]),
    'D': lambda qc, pair: None,
}

Далее, создадим процедуру, которая в качестве аргументов получает две пары кубит, основной и соседней вершины, и проверяет наличие связи между ними. Также в процедуру передаем результирующий кубит, который заранее подготовлен в состоянии $| 1 \rangle$ .

def find_disconnection(qc, pair_1, pair_2, ancilla_qubit, result_qubit):
    
    for letter_1 in connections.keys():
    
        vertex_to_find = [x for x in vertex_names.keys() if x not in connections[letter_1]]
        
        if len(vertex_to_find) > 0:

            vertex_to_11[letter_1](qc, pair_1)
            qc.toffoli(*pair_1, ancilla_qubit)
                        
            for letter_2 in vertex_to_find:
                vertex_to_11[letter_2](qc, pair_2)
                qc.mct([*pair_2, ancilla_qubit], result_qubit)
                vertex_to_11[letter_2](qc, pair_2)
            
            qc.toffoli(*pair_1, ancilla_qubit)
            vertex_to_11[letter_1](qc, pair_1)

Эта процедура проверяет одну пару рядом стоящих вершин на предмет существования связи между ними. Если подобной связи нет, то она инвертирует результирующий кубит (1 → 0) процедуры, что не позволит оракулу объявить данную комбинацию «хорошей».

5. Оператор диффузии

Оператор диффузии Гровера в матричном выражении представляет собой обычную единичную матрицу, все диагональные элементы которой равны -1 за исключением самого левого верхнего элемента, который равен 1. Оператор инвертирует фазу любого вектора, кроме вектора $| 0 \rangle$ .

$U_{s} = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & -1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & -1 \end{pmatrix}$

Пример действия оператора на вектор $| 0 \rangle$ :

$U_{s} | 0 \rangle = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & -1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \\$

Пример действия оператора на любой другой вектор:

$U_{s} | \psi \rangle = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & -1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \\ \vdots \\ 0 \end{pmatrix} = -| \psi \rangle$

«Сочинять» конфигурацию вентилей для оператора диффузии нет необходимости, он уже разработан. Для набора из n кубит оператор будет выглядеть следующим образом:

Теперь напишем функцию, которая выражает оператор диффузии Гровера. Функцию сделаем универсальной, она на вход будет принимать любое количество кубит.

def diffusion(qc, qubits):

    qc.h(qubits)
    qc.x(qubits)

    qc.h(qubits[-1])

    length = len(qubits)

		if length > 3:
				qc.mct(qubits[0:-1], qubits[-1])
		elif length == 3:
				qc.toffoli(qubits[0:-1], qubits[2])
		elif length == 2:
				qc.cx(qubits[0], qubits[1])

    qc.h(qubits[-1])

    qc.x(qubits)
    qc.h(qubits)

В качестве центрального элемента оператора используется один из трех вентилей:

когда на вход поступают всего 2 кубита — простой вентиль CNOT
когда 3 кубита — вентиль Тоффоли
когда 4 и более кубита — вентиль Тоффоли для многих кубит

Доработка оператора диффузии Гровера

Поскольку для создания начальной суперпозиции входных кубит мы не везде использовали однокубитный вентиль Адамара, нам потребуется видоизменить оператор диффузии.

В первоначальном виде оператор диффузии Гровера на входе применяет ко всем входным кубитам вентиль Адамара, тем самым как бы возвращая кубиты из суперпозиции в обычное несвязанное состояние. На выходе оператор снова применяет вентили Адамара для создания суперпозиции.

Однако, на шаге создания суперпозиции мы применили специальные операторы для исключения ненужных комбинаций из первой и четвертой пары кубит, а вентиль Адамара применили только ко второй и третьей.

Соответственно, для нашего алгоритма мы отключим в операторе диффузии Гровера входные и выходные вентили Адамара:

def diffusion(qc, qubits):
    # qc.h(qubits)
    qc.x(qubits)
    qc.h(qubits[-1])
    
    length = len(qubits)
    
    if length > 3:
        qc.mct(qubits[0:-1], qubits[-1])
    elif length == 3:
        qc.toffoli(qubits[0:-1], qubits[2])
    elif length == 2:
        qc.cx(qubits[0], qubits[1])
    
    qc.h(qubits[-1])
    qc.x(qubits)
    # qc.h(qubits)

Теперь он выглядит так:

Адаптированный под задачу оператор диффузии Гровера

А перед вызовом оператора будем применять преобразование, обратное созданию суперпозиции, после оператора — снова создание суперпозиции:

exclude_00(qc, qr[0:2], reverse=True)
qc.h(qr[2:6])
exclude_00(qc, qr[6:8], reverse=True)

diffusion(qc, qr[0:8])

exclude_00(qc, qr[0:2])
qc.h(qr[2:6])
exclude_00(qc, qr[6:8])

Тут нам и пригодилась инверсная версия процедуры исключения комбинации 00 из суперпозиции.

5. Собираем все вместе

Мы не будем подробно рассматривать принципы работы алгоритма Гровера с его учебными примерами, а сразу приступим к его реализации. Рассчитаем число итераций, пусть n — число входных кубит для оракула, в нашем случае оно равно 8, тогда количество итераций алгоритма Гровера должно быть следующим:

$k = \frac{\pi}{4} \sqrt{n} = \frac{\pi}{4} \sqrt{8} = 2,22$

То есть, нам потребуется всего 2 итерации алгоритма для получения отчетливого результата.

5.1. Общая схема

Все составляющие алгоритма мы рассмотрели, начинаем сборку элементов в единую рабочую цепь. Общая схема выглядит следующим образом:

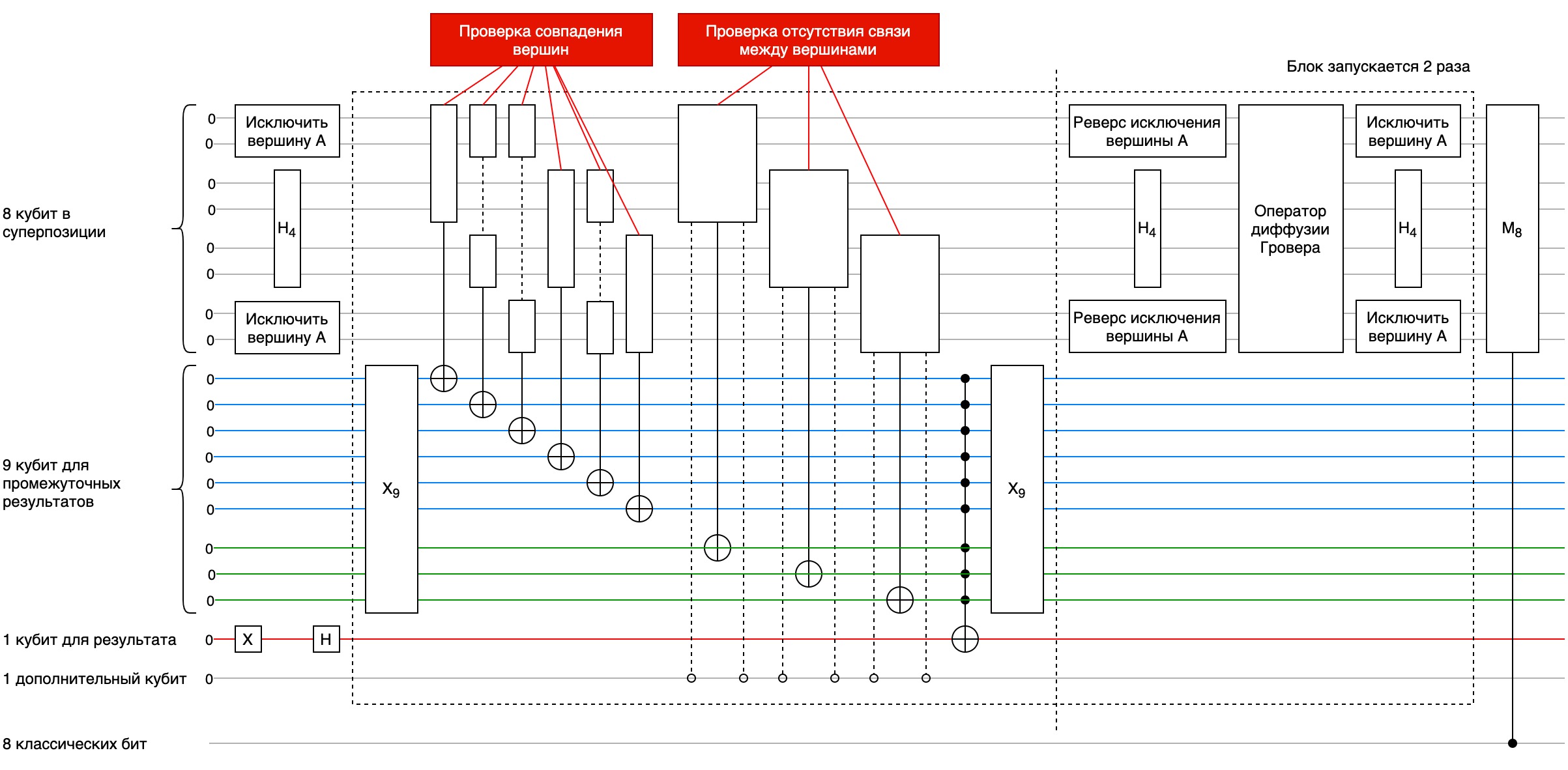
Скачиваем и устанавливаем библиотеки Qiskit, NumPy и Matplotlib для Python.

> pip3 install qiskit numpy matplotlib

Импортируем необходимые библиотеки.

import numpy as np
from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit, Aer, execute

Заранее подготовим процедуру поиска совпадений вершин.

def find_equality(...):
    # См. код процедуры выше

Заводим необходимые для работы переменные и вспомогательные функции:

vertex_names = {
    'A': '00',
    'B': '01',
    'C': '10',
    'D': '11',
}

connections = {
    'A': ['C','D'],
    'B': ['C','D'],
    'C': ['A','B','D'],
    'D': ['A','B','C'],
}

vertex_to_11 = {
    'A': lambda qc, pair: qc.x(pair),
    'B': lambda qc, pair: qc.x(pair[0]),
    'C': lambda qc, pair: qc.x(pair[1]),
    'D': lambda qc, pair: None,
}

Готовим процедуру поиска несвязанных вершин и оператор диффузии.

def find_disconnection(...):
    # См. код процедуры find_disconnection выше

def diffusion(...):
    # См. код процедуры diffusion выше

Подготавливаем процедуру для исключения ненужных вершин из суперпозиции:

theta = 2 * np.arccos(1 / np.sqrt(3))

def exclude_00(qc, pair, reverse=False):
    # См. код процедуры exclude_00

Теперь необходимо решить, сколько нам всего потребуется кубит:

Индексы	Число кубит	Назначение
0-7	8	Комбинации вершин в маршруте
8-13	6	Промежуточные результаты поиска совпадающих вершин
14-16	3	Промежуточные результаты поиска несвязанных вершин
17	1	Результирующий кубит
18	1	Дополнительный кубит для процедуры поиска несвязанных вершин

Итого, нам потребуются 19 кубит. Для измерения результата также необходимо зарезервировать 8 обычных бит.

Создаем квантовую цепь:

qr = QuantumRegister(19)
cr = ClassicalRegister(8)
qc = QuantumCircuit(qr, cr)

Создаем суперпозицию:

exclude_00(qc, qr[0:2])
qc.h(qr[2:6])
exclude_00(qc, qr[6:8])

Подготавливаем результирующий кубит:

qc.x(17)
qc.h(17)

Пишем цикл, который дважды запускает оракул и оператор диффузии Гровера.

pairs = [
    [[qr[0],qr[1]], [qr[2],qr[3]]],
    [[qr[0],qr[1]], [qr[4],qr[5]]],
    [[qr[0],qr[1]], [qr[6],qr[7]]],
    [[qr[2],qr[3]], [qr[4],qr[5]]],
    [[qr[2],qr[3]], [qr[6],qr[7]]],
    [[qr[4],qr[5]], [qr[6],qr[7]]],
]

for i in range(2):

    # Oracle
        
    qc.x(qr[8:17])
    
    for i, pair in enumerate(pairs):    
        find_equality(qc, pair[0], pair[1], qr[8 + i])
    
    find_disconnection(qc, pair_1=qr[2:4], pair_2=qr[0:2], ancilla_qubit=qr[18], result_qubit=qr[14])
    find_disconnection(qc, pair_1=qr[4:6], pair_2=qr[2:4], ancilla_qubit=qr[18], result_qubit=qr[15])
    find_disconnection(qc, pair_1=qr[6:8], pair_2=qr[4:6], ancilla_qubit=qr[18], result_qubit=qr[16])
    
    # Store result
    
    qc.mct(qr[8:17], qr[17])
    
    # Oracle (reverse)
    
    find_disconnection(qc, pair_1=qr[6:8], pair_2=qr[4:6], ancilla_qubit=qr[18], result_qubit=qr[16])
    find_disconnection(qc, pair_1=qr[4:6], pair_2=qr[2:4], ancilla_qubit=qr[18], result_qubit=qr[15])
    find_disconnection(qc, pair_1=qr[2:4], pair_2=qr[0:2], ancilla_qubit=qr[18], result_qubit=qr[14])

    for i, pair in enumerate(pairs):    
        find_equality(qc, pair[0], pair[1], qr[8 + i])
    
    qc.x(qr[8:17])

    # Diffuser
    
    exclude_00(qc, qr[0:2], reverse=True)
    qc.h(qr[2:6])
    exclude_00(qc, qr[6:8], reverse=True)
    
    diffusion(qc, qr[0:8])
    
    exclude_00(qc, qr[0:2])
    qc.h(qr[2:6])
    exclude_00(qc, qr[6:8])

При запуске нескольких итераций необходимо «подчищать» дополнительные кубиты для экономии. Поэтому после сохранения результата работы оракула необходимо выполнить обратные процедуры, чтобы вернуть к исходному состоянию 1 все кубиты промежуточных результатов и состоянию 0 все дополнительные кубиты, иначе вторая итерация будет выполнена некорректно. Обратная процедура иногда бывает эквивалентна исходной, а иногда в ней требуется выполнить все шаги в обратном порядке. Все зависит от конфигурации вентилей, если повторное применение в обратном порядке возвращает систему в первоначальное состояние, то нет необходимости для процедуры писать инверсный вариант.

Измерение результата:

qc.measure(qr[0:8], cr)

Итак, схема готова, теперь необходимо ее запустить.

Поскольку всего комбинаций 144, из них удачных только 4, то нам потребуется запустить алгоритм «приличное» число раз, чтобы отчетливо увидеть распределение вероятности удачных и неудачных маршрутов.

Запускаем алгоритм на симуляторе.

simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend = simulator, shots = 1000).result()
counts = result.get_counts()
print(counts)

Получаем результат.

{'10011001': 1, ..., '11000110': 146, ..., '01100010': 4}

Метод measure класса QuantumCirquit возвращает ответ в виде массива с ключами, где каждый ключ соответствует комбинации кубит, а значение есть частота появления этой комбинации среди всех запусков алгоритма. Ключ представляет кубиты с 0-го по n-й справа налево, как принято при записи двоичных и десятичных чисел. Например:

$\stackrel{7}{0}\stackrel{6}{0}\stackrel{5}{1}\stackrel{4}{0}\stackrel{3}{1}\stackrel{2}{0}\stackrel{1}{0}\stackrel{0}{1}$

Кроме того, этот массив не отсортирован, и найти в нем наиболее вероятные варианты тяжело. Напишем небольшое выражение, которое придаст результату «человекопонятный» вид.

answers = {''.join(dict(zip(map(lambda x: x[::-1], vertex_names.values()), vertex_names.keys()))[k[i*2:i*2+2]]
           for i in range(len(k)//2)): v
           for k, v in {item[0]: item[1]
           for item in sorted(counts.items(), key=lambda x:x[1], reverse=True)}.items()}
print(answers)

Получаем результат.

{'CADB': 161, 'BDAC': 135, 'DACB': 130, 'BCAD': 127, 'DCAC': 8, ... }

Теперь мы видим, что наибольшую частоту имеют маршруты:

{
    'CADB': 161,
    'BDAC': 135,
    'DACB': 130,
    'BCAD': 127
}

Частота остальны значительно ниже. Для наглядности построим гистограмму распределения вероятностей ответов:

from qiskit.visualization import plot_histogram
plot_histogram(counts)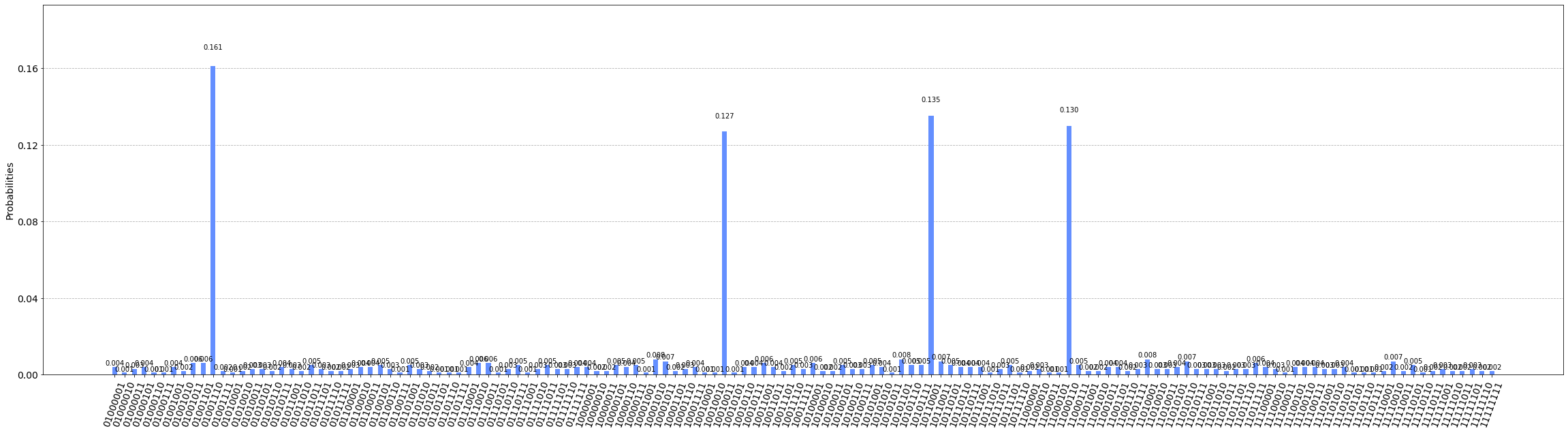

Распределение частоты появления всех возможных маршрутов

6. Выводы

Используя квантовый алгоритм Гровера мы с вами нашли гамильтоновы пути в графе с 5-ю вершинами. Практическое применение алгоритма Гровера требует учета ряда особенностей:

Характер суперпозиции влияет на оператор диффузии.
При запуске нескольких итераций необходимо применять инверсию оракула для экономии дополнительных кубит.
Оракул должен готовиться особым образом, входящие в него процедуры должны обнаруживать «нарушения условий», оракул инвертирует фазу комбинации только когда нет ни одного «нарушения».

Решение не универсальное, его невозможно применить к другой конфигурации ребер в графе, не говоря уже о большем числе вершин. Для создания универсального инструмента необходимо учесть следующие аспекты:

Решения вообще может не быть, тогда вероятность всех маршрутов будет примерно одинаковая.
Заранее неизвестно количество ответов. Зная это число, можно значительно сократить объем вычислений, необходимо применить к задаче алгоритмы поиска числа решений.
Решение не подходит для числа вершин, отличного от 5-ти как в большую так и в меньшую сторону. Потребуется значительная переработка для адаптации.
Рост числа вершин значительно увеличивает число кубит для обнаружения неуникальных вершин.

Надеюсь, статья будет кому-либо полезной:)

Ссылка на код алгоритма в репозитории GitHub

Комментарии (4)

zuborg
03.11.2021 18:29
#23664496
+2
Спасибо за статью.

Но непонятно два момента ;)

Во первых, почему решений только 4, если их значительно больше - BACD, BADC, BCAD, BDAC, CABD, CADB, CBAD, CDAB, DABC, DACB, DBAC, DCAB?

Во вторых - почему алгоритм нашел два решения с первой вершиной "C", но только по одному для "B" и "D", хотя граф симметричный относительно B, C и D?
1. nkochelev Автор
  04.11.2021 11:55
  #23666582
  Спасибо за комментарий! Обнаружил ошибки невнимательности при подготовке иллюстраций: в изображении графа ошибочно соединил вершины A и B, хотя изначально задача сформулирована и решена для случая, когда этой связи нет.
  
  Изображения поправил, теперь должно быть видно, что решений всего 4 и симметрии относительно вершин нет.

slonopotamus
04.11.2021 15:39
#23667358
удалено

sergei_shirkin
11.11.2021 14:26
#23694634
Спасибо за статью, очень познавательно.
В формуле числа итераций, мне кажется, ошибка. Под корнем вместо n (число кубитов) должно быть N/K, где N - число всех возможных состояний и K - число искомых состояний (в примере из статьи это 4), причем эта формула оценочная и только для больших N, а в этом примере можно число итераций посчитать напрямую через угол между гиперплоскостью всех состояний кроме искомых и гиперплоскостью искомых состояний. Если этот угол поставить в формулу (2i + 1)*угол (где i - число итераций), то должно получиться около 90 градусов, для того, чтобы при измерении получались в основном только искомые состояния.

И еще по поводу слова "кубит" - оно склоняется по падежам (https://ru.wiktionary.org/wiki/кубит):