Предположим, нам необходимо выполнить поиск в большой коллекции литературных произведений, используя запросы, требующие точного соответствия названия, автора или других легко индексируемых критериев. Такая задача хорошо подходит для реляционной базы данных и такого языка, как SQL. Однако, если мы хотим использовать более абстрактные запросы, такие как «Поэма о гражданской войне», становится невозможным полагаться на наивные метрики сходства вроде количества общих слов между двумя фразами. Например, запрос «научная фантастика» больше связан с «будущим», чем, например, с «наукой о Земле», несмотря на то, что в первом случае у нас нет общих слов, а во втором есть общекоренное слово к одному из слов запроса.

Машинное обучение значительно улучшило способность компьютеров понимать семантику языка и, следовательно, отвечать на эти абстрактные запросы. Современные модели машинного обучения могут преобразовывать входные данные, такие как текст и изображения, в эмбеддинги — многомерные векторы, обученные таким образом, чтобы более похожие входные данные располагались ближе друг к другу в векторном пространстве. Таким образом, для данного запроса мы можем вычислить его эмбеддинг и найти литературные произведения, эмбеддинги которых будут ближе всего к запросу. Так, машинное обучение превратило абстрактную и ранее трудно определяемую задачу в строго математическую. Однако остается проблема вычислений: как быстро найти ближайшие эмбеддинги набора данных для данного эмбеддинга запроса? Набор эмбеддингов часто слишком велик для поиска перебором, а его высокая размерность затрудняет оптимизацию отсечением.

В своей статье на конференции ICML 2020 «Accelerating Large-Scale Inference with Anisotropic Vector Quantization» авторы решают эту проблему, сосредоточив внимание на том, как сжимать векторы из набора данных для быстрого вычисления приближенных расстояний, и предлагают новый метод сжатия, который значительно повышает точность по сравнению с предыдущими работами по данной теме. Этот метод используется в недавно созданной авторами библиотеке поиска схожих векторов с открытым исходным кодом (ScaNN) и позволяет в два раза превзойти другие библиотеки поиска схожих векторов, по данным ann-benchmarks.com.

Важность поиска по векторному сходству

Поиск на основе эмбеддингов — это метод, который эффективен при ответах на запросы, которые полагаются на семантическое понимание, а не на простые индексируемые характеристики. В этом методе модели машинного обучения учатся отображать запросы и элементы базы данных в общее векторное пространство, так что расстояние между эмбеддингами несет семантическое значение, т.е. похожие элементы расположены ближе друг к другу.

Модель нейронной сети с двумя «башнями», проиллюстрированная выше, представляет собой особый тип поиска на основе эмбеддингов, при котором запросы и элементы базы данных отображаются в векторное пространство двумя соответствующими нейронными сетями. В этом примере модель отвечает на запросы на естественном языке для гипотетической литературной базы данных.

Чтобы ответить на запрос с помощью этого подхода, система должна сначала сопоставить запрос с векторным пространством. Затем она должна найти среди всех эмбеддингов базы данных наиболее близкие к запросу; это проблема поиска ближайшего соседа (nearest neighbor search). Один из наиболее распространенных способов определить сходство эмбеддингов запроса и базы данных — по их скалярному произведению; этот тип поиска ближайшего соседа известен как поиск максимального скалярного произведения (maximum inner-product search, MIPS).

Поскольку размер базы данных может легко исчисляться миллионами или даже миллиардами, MIPS часто становится бутылочным горлышком с точки зрения скорости вывода, а поиск полным перебором оказывается непрактичным. Все это свидетельствует о необходимости использования приближенных алгоритмов MIPS, которые готовы пожертвовать высокой точностью ради значительного ускорения по сравнению с поиском методом грубой силы.

Новый подход квантизации для MIPS

Несколько современных решений для MIPS основаны на сжатии элементов базы данных, так что аппроксимация их скалярного произведения может быть вычислена лишь за часть времени, затрачиваемого на решение методом грубой силы. Это сжатие обычно выполняется с помощью выученной квантизации, когда кодовая книга векторов выучивается из базы данных и используется для приближенного представления ее элементов.

Предыдущие схемы проводили векторную квантизацию элементов базы данных с целью минимизировать среднее расстояние между каждым вектором и его квантизованной формой . Хотя это полезный показатель, его оптимизация не эквивалентна оптимизации точности поиска ближайшего соседа. Ключевая идея, лежащая в основе статьи авторов, заключается в том, что более высокое среднее расстояние между векторами может фактически привести к более высокой точности MIPS.

Интуиция этого результата проиллюстрирована ниже. Предположим, у нас есть два эмбеддинга базы данных и , и мы должны квантизовать каждый в один из двух центров: или . Наша цель — квантизовать каждый в так, чтобы скалярное произведение было как можно более похоже на исходное скалярное произведение . Это можно представить себе как создание такой проекции , которая была бы как можно более похожа на проекцию на . В традиционном подходе к квантизации (слева) авторы выбирают ближайший центр для каждого , что приводит к неправильному относительному ранжированию двух точек: больше, чем , даже если меньше, чем ! Если вместо этого присвоить переменной и переменной , мы получим правильное ранжирование. Это показано на рисунке ниже.

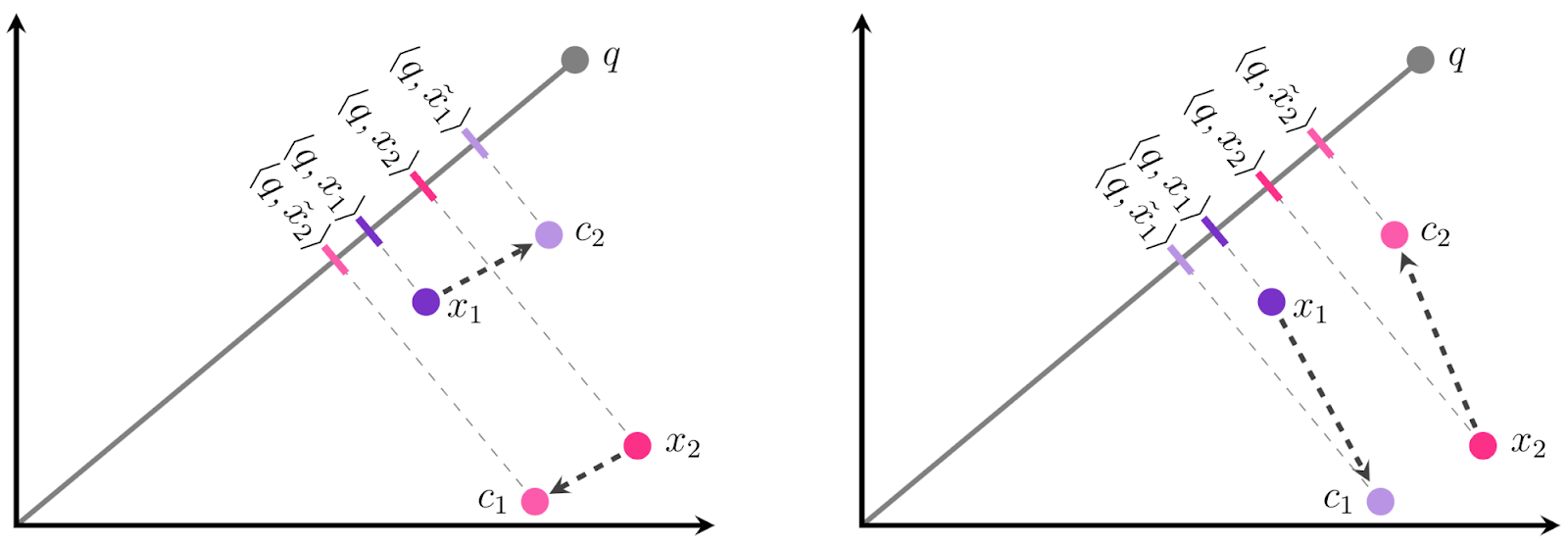
Цель состоит в том, чтобы квантизовать каждый в или . Традиционная квантизация (слева) приводит к неправильному порядку и для этого запроса. Несмотря на то, что предложенный авторами подход (справа) выбирает центры дальше от точек данных, это фактически приводит к меньшей ошибке скалярного произведения и более высокой точности.

Оказывается, направление имеет значение так же, как и величина — даже несмотря на то, что дальше от , чем , смещен от в направлении, почти полностью ортогональном , в то время как смещение параллельно (для применимо то же самое, но в обратную сторону). Ошибка в параллельном направлении гораздо более вредна в проблематике MIPS, потому что она непропорционально влияет на высокие скалярные произведения, которые по определению являются теми, которые MIPS пытается точно оценить.

Основываясь на этой интуиции, авторы придают больший вес ошибки квантизации, которая параллельна исходному вектору. Новую технику квантизации назвали анизотропной векторной квантизацией из-за направленной зависимости ее функции потерь. Способность этого метода повысить ошибку квантизации более маленьких скалярных произведений в обмен на высокую точность для больших скалярных произведений является ключевым нововведением и источником повышения производительности.

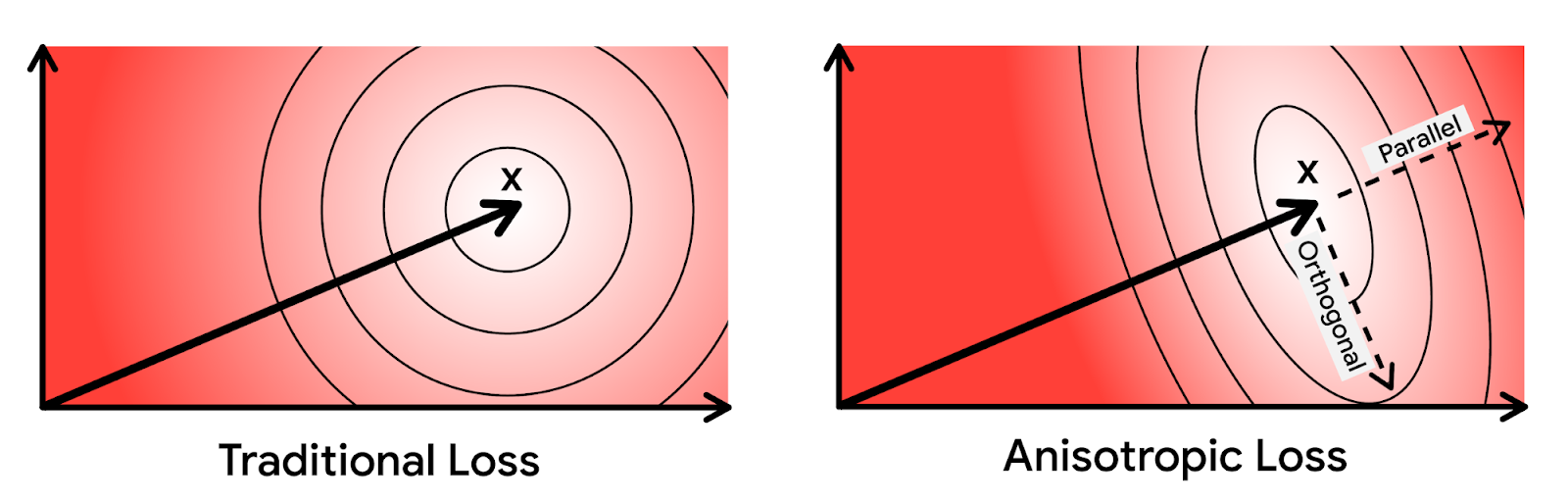
На приведенных выше диаграммах эллипсами обозначены контуры равных значений функции потерь. При анизотропной векторной квантизации ошибка, параллельная исходной точке данных , штрафуется больше.

Анизотропная векторная квантизация в ScaNN

Анизотропная векторная квантизация позволяет ScaNN лучше оценивать скалярные произведения, которые, вероятно, будут в топ-k результатах MIPS, и, следовательно, достигать более высокой точности. В тесте glove-100-angular от ann-benchmarks.com библиотека ScaNN превзошла одиннадцать других тщательно разработанных библиотек поиска по векторному сходству, обрабатывая примерно вдвое больше запросов в секунду при заданной точности по сравнению с ближайшим решением.

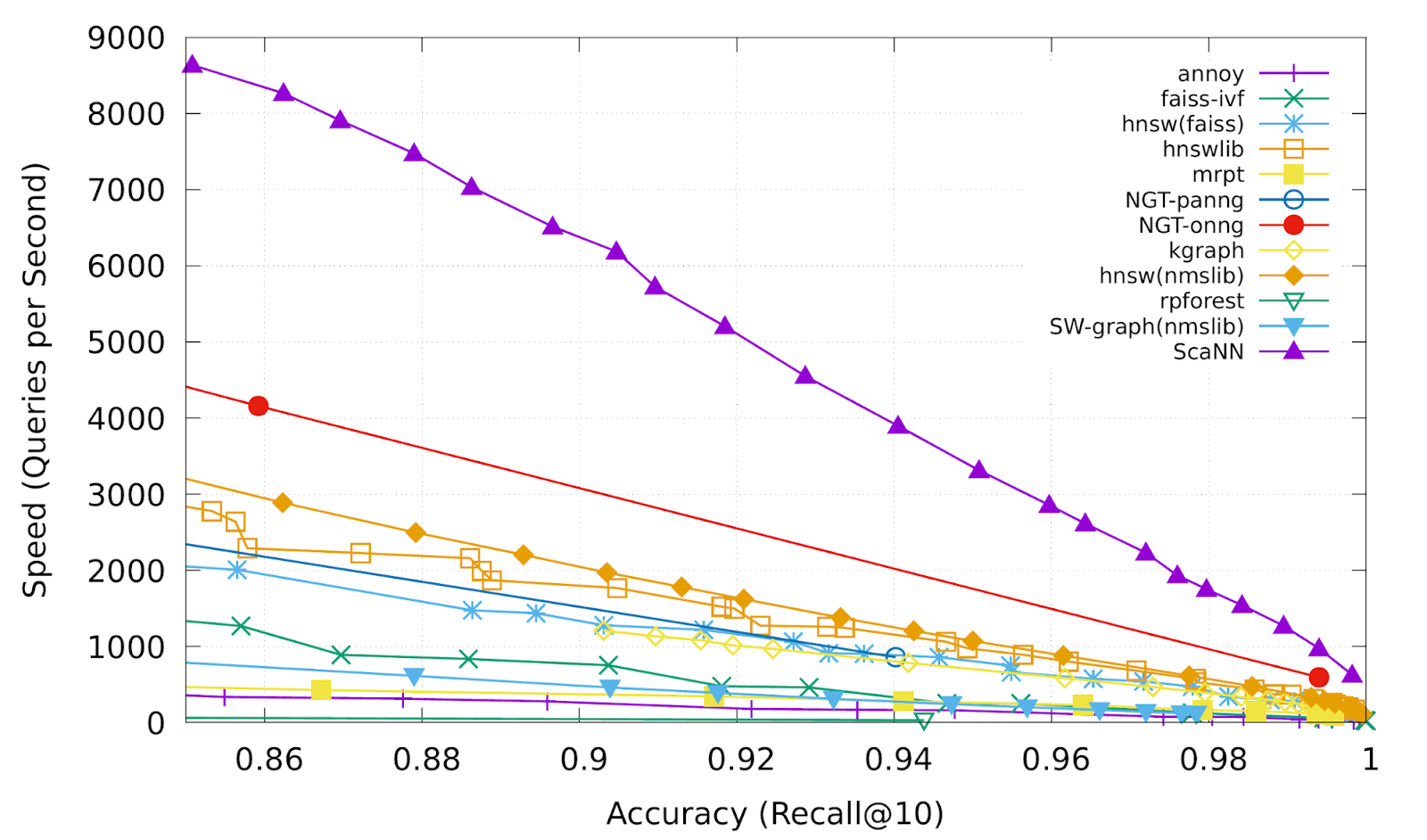
Recall@k — это распространенная метрика точности поиска ближайшего соседа, которая измеряет долю истинных ближайших k соседей, присутствующих в возвращенных алгоритмом k соседях. ScaNN (верхняя пурпурная линия) неизменно обеспечивает самую высокую производительность в различных точках компромисса между скоростью и точностью.

ScaNN — это библиотека с открытым исходным кодом, и вы можете протестировать ее самостоятельно на GitHub. Библиотека может быть установлена напрямую через pip и имеет интерфейсы для входных данных формата TensorFlow и Numpy. Дополнительные инструкции по установке и настройке ScaNN см. в репозитории на GitHub.

Заключение

Изменение цели векторной квантизации для ее согласования с целями MIPS позволило авторам достичь высокого уровня производительности в бенчмарках поиска ближайшего соседа, что является ключевым показателем эффективности поиска на основе эмбеддингов. Хотя анизотропная векторная квантизация является важным методом, авторы полагают, что это всего лишь один пример повышения производительности, достижимой за счет оптимизации алгоритмов для конечной цели повышения точности поиска, а не для промежуточной цели, такой как искажение сжатия.

Авторы

• Автор оригинала – Philip Sun
• Перевод – Смирнова Екатерина
• Редактирование и вёрстка – Шкарин Сергей