Теорема о свёртке утверждает, что преобразование Фурье от свёртки двух функций является произведением их Фурье образов:

Как следствие, свёртку двух функций можно вычислить путём обратного преобразования Фурье:

Когда свёртку не удаётся получить аналитически, использование теоремы позволяет вместо численного интегрирования воспользоваться алгоритмом быстрого преобразования Фурье и существенно ускорить процесс вычислений. В ходе решения возникшей у меня задачи мне не удалось найти в интернете достаточно подробного описания алгоритма действий, поэтому я решил изложить его здесь, во-первых, как памятку для себя и во-вторых, на случай если это окажется полезным кому-то ещё. Не претендуя на общность изложения, ниже я приведу примеры найденных решений для функций от одной и от двух переменных.

Функция от одной переменной

Допустим, нам нужно вычислить свёртку функций

причём имеется в виду, что нас интересует только действительная часть области значений функции, то есть область её определения лежит в интервале . Интеграл функции в этом интервале равен 1, а преобразование Фурье вычисляется аналитически:

где - функция Бесселя первого рода. Фурье образ функции Гаусса:

Дискретным преобразованием Фурье (ДПФ) называется метод вычислений, в котором и функция и ее преобразование заменяются дискретными аналогами. Быстрое преобразование Фурье (БПФ) относится к способу эффективного вычисления ДПФ с использованием симметрии в вычисляемых условиях. Симметрия наивысшая, когда число узлов, в которых вычисляется значение функции, и число гармоник,  являются степенью двойки. В библиотеке SciPy с открытым исходным кодом для работы с БПФ предназначен модуль scipy.fft. Для того, чтобы вычислить искомую свёртку методом БФП, нужно задать интересующую нас область определения результата и задать количество узлов разбиения, в которых мы хотим получить значение свёртки.

Выберем область определения , где и- положительные вещественные числа, которые мы будем считать размерными, например, пусть это будут сантиметры. Разобъём этот интервал на одинаковых отрезков, длина каждого из которых равна . Интервал называется шагом дискретизации и определяет расстояние между соседними узлами разбиения шкалы . Обратная величина называется частотой дискретизации и в нашем примере измеряется в обратных сантиметрах.

В шкале частот нашему диапазону шкалыбудет соответствовать набор из положительных и отрицательных гармоник разложения Фурье. Если - чётное, последовательность частот, которая генерируется функцией scipy.fft.fftfreq, будет такая:

Если функция, которую мы ищем, вещественна (не имеет мнимой части), положительные частоты в последовательности являются сопряженными величинами отрицательных частот, за счёт этого можно примерно в два раза сократить время вычислений. Для получения укороченной (без отрицательных частот) последовательности используется функция scipy.fft.rfftfreq. Для выполнения прямого и обратного преобразований Фурье для вещественного сигнала предназначены функции scipy.fft.rfft и scipy.fft.irfft соответственно. Функция scipy.fft.fftshift располагает компоненту с нулевой частотой в середине частотного спектра, а scipy.fft.ifftshift осуществляет обратное преобразование. Ниже приведён код для вычисления свёртки:

import numpy as np
from scipy.special import j0 as BesselJ0 
import scipy.fft as FFT
from matplotlib import pyplot as plt

π    = np.pi
σ    = 0.01
R    = 1.5    # интервал, в котором вычисляется свёртка
Nx   = 4096   # число разбиений по оси x
Dx   = 2*R/Nx # шаг дискретизации
x    = np.linspace(0.5*Dx-R, R-0.5*Dx, num = Nx)
u    = FFT.rfftfreq(Nx//16, d = 16*Dx) # цифровой ФНЧ
J0   = BesselJ0(2*π*u)*np.exp(-2*(π*σ*u)**2)
y    = FFT.ifftshift(FFT.irfft(J0, n=Nx, norm='forward'))

plt.subplot(211)
plt.plot(u, J0, 'r-', label='спектр частот')
plt.xlabel('u, [1/см]')
plt.grid(True); plt.legend()
plt.subplot(212)
plt.plot(x, y, 'r-', label='результат свёртки')
plt.xlabel('x, [см]')
plt.grid(True); plt.legend()
plt.show()

Результат представлен на картинке. Как видно из спектра частот, амплитуда гармоник экспоненциально падает с ростом частоты (из-за , см. выше) , поэтому число вычисляемых гармоник уменьшено в 16 раз с помощью "цифрового ФНЧ".

Функция от двух переменных

Перейдем к двумерному случаю. Пусть

где и различны. Пользуясь полученными выше формулами и рецептами, создадим код для вычисления свёртки этих функций:

import numpy as np
from scipy.special import j0 as BesselJ0 
import scipy.fft as FFT
import matplotlib.pyplot as plt

π    = np.pi
σx   = 0.1 
σy   = 0.05
R    = 1.5
N    = 2048
D    = 2*R/N
s    = np.linspace(0.5*D-R, R-0.5*D, num = N)
f    = FFT.fftshift(FFT.fftfreq(N//4, d = 4*D))
x,y  = np.meshgrid(s,s)
u,v  = np.meshgrid(f,f)
J    = BesselJ0(2*π*(u**2 + v**2)**0.5)*np.exp(-2*π*π*((σx*u)**2 + (σy*v)**2))
z    = np.abs(FFT.ifftshift(FFT.ifft2(J, s=[N,N], workers=-1, norm='forward')))

plt.figure(figsize=(16, 9))
levels = np.linspace(J.min(), J.max(), 16)
plt.subplot(121)
plt.contourf(u, v, J, levels)
plt.colorbar()
plt.xlim(-5,5); plt.xlabel('u, [1/см]')
plt.ylim(-5,5); plt.ylabel('v, [1/см]')
plt.subplot(122)
levels = np.linspace(z.min(), z.max(), 16)
plt.contourf(x, y, z, levels)
plt.colorbar()
plt.xlabel('x, [см]')
plt.ylabel('y, [см]')
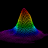
plt.show()

Основное изменение в коде, по сравнению с одномерной задачей, состоит в использовании scipy.fft.fftfreq вместо scipy.fft.rfftfreq и scipy.fft.ifft2 вместо scipy.fft.irfft. Опция workers=-1 в функции ifft2 позволяет параллельно использовать все имеющиеся в системе процессоры. Результат вычислений представлен на картинке:

Заключение

Вот вроде бы и всё о чём я хотел написать. Буду рад критике, вопросам и предложениям. Всех с наступающим 2022!