
Регрессия к среднему – это распространенный статистический феномен, который может наводить нас на ошибочные выводы, когда мы наблюдаем, что происходит в мире. Умение распознавать, в каких случаях мы имеем дело именно с регрессией к среднему, помогает избежать ложной интерпретации данных и не замечать паттернов там, где их нет.
Важно свести к минимуму количество неверных суждений и устранить слабые места в наших рассуждениях. В этом нам могут помочь знания о регрессии к среднему.
Лауреат Нобелевской премии, психолог Даниэль Канеман написал книгу о предубеждениях, мешающих нам здраво рассуждать и искажающих наше восприятие реальности. Оказывается, есть целый набор логических ошибок, которые мы совершаем, так как наша интуиция и наш мозг не слишком хорошо справляются с простой статистикой. Одна из тех ошибок, которые автор исследует в упомянутой книге Думай медленно, решай быстро – это пресловутая регрессия к среднему.
Феномен регрессии к среднему впервые проработал сэр Френсис Гальтон. Правило таково, что в любом ряду сложных явлений, зависящих от множества переменных и сопряженных с фактором вероятности, после экстремальных результатов обычно следуют более умеренные.
В книге Seeking Wisdom («Поиск истины») Питер Бевелин приводит такой пример: Джон недоволен производительностью труда новых работников, поэтому он записал их на программу повышения квалификации, в ходе которой измерял навыки сотрудника:
Их баллы повысились по сравнению с первыми тестами. Какой вывод делает Джон: «Навыки улучшились благодаря программе повышения квалификации». Но это не обязательно так. Такое повышение баллов может возникать в результате регрессии к среднему. Поскольку этих индивидов позиционировали как обитателей «нижнего края» шкалы навыков, они могли показать улучшение показателей, даже если бы не участвовали в программе повышения квалификации. А их плохая успешность на первом этапе могла объясняться множеством причин – стрессом, усталостью, нездоровьем, тем, что их отвлекали, т.д. Их истинный уровень подготовки, пожалуй, остался неизменным.
Наша производительность всегда колеблется около некоторого среднего значения, отражающего истинную производительность. Крайнее значение производительности, достигнутое в этот раз, в следующий раз может быть «не таким крайним». Почему? Потому что тестовые измерения никогда не могут быть точными. В их составе есть и истинная составляющая, и составляющая ошибки. Любые крайние значения при измерениях в той или иной степени случайны. Вероятно, при повторном измерении производительности влияние случайного компонента оказывается меньше, чем при первом.
Если мы станем делать что-либо иначе, чем в первый раз, только потому, что в первый раз у нас не получилось, то весьма вероятно, что во второй раз попытка выйдет более успешной, даже если новый подход, в сущности, не лучше или даже хуже старого.
Вот одна из причин, по которым опасно экстраполировать результаты, достигнутые на маленьких выборках, поскольку их данные могут неадекватно представлять все распределение. По той же причине Джеймс Марч настаивает, что, чем дольше человек остается на одном рабочем месте, «тем меньше разница между его фиксируемой производительностью и фактическими способностями». В краткосрочной перспективе может произойти что угодно, особенно, если дело, за которое вы беретесь, зависит как от умения, так и от везения. (Соотношение умения и везения также влияет на регрессию к среднему.)
Регрессия к среднему – это не закон природы. Просто статистическая тенденция. И может потребоваться много времени, пока она произойдет.
— Питер Бевелин
Регрессия к среднему
Эффекты регрессии к среднему часто можно наблюдать в спорте, где такой эффект порождает массу необоснованных спекуляций.
В книге «Думай медленно, решай быстро», Канеман вспоминает, как смотрел соревнования лыжников по прыжкам с трамплина – в этом виде спорта итоговые очки складываются из комбинации двух попыток. Канеман, зная о регрессии к среднему, просто поразился прогнозам комментатора по поводу второго прыжка. Он пишет:
«Норвежец отлично выполнил первый прыжок, теперь спортсмен напряжен, постарается защитить свою позицию и, вероятнее всего, прыгнет хуже» или «Шведский спортсмен плохо выполнил первый прыжок, он знает, что ему нечего терять, будет расслаблен, и это поможет ему прыгнуть лучше»
Канеман пишет, что комментатор заметил регрессию к среднему и придумал историю, в основе которой нет никаких причинно-следственных связей (см. ошибка интерпретации). Это не означает, что его объяснение не могло быть верным. Может быть, если бы мы измерили у лыжников пульс перед каждым прыжком, то заметили бы, что спортсмен более расслаблен, если первый прыжок не удался. Но суть не в этом. Суть в том, что при наличии фактора везения в игру вступает регрессия к среднему, а в случае с результатом первого прыжка так и было.
Этот урок из спорта актуален для любого вида деятельности, в котором есть вероятностный фактор. Часто, достигая прогресса в каком-то деле или, наоборот, не достигая его, мы придумываем некое собственное влияние на этот процесс.
В реальности наука о производительности сложна и ситуативно-зависима, и зачастую многие факторы, которые, на наш взгляд, в наших руках, на самом деле являются случайными.
В примере с лыжными прыжками с трамплина сильный встречный ветер может привести к тому, что даже самый лучший спортсмен покажет посредственный результат. Аналогично, сильный попутный ветер и хорошее состояние лыж могут быть на руку не самому сильному спортсмену, и серьезно, но кратковременно, улучшить его результаты. Но такие эффекты исчезнут, как только условия изменятся, и результаты снова сдвинутся к нормальным.
Это может иметь серьезные последствия для тренерской работы и отслеживания производительности. Правила регрессии подсказывают, что, при оценке эффективности найма, мы больше ориентируемся на послужной список, чем на исходы конкретных ситуаций, в которых оказывался человек. В противном случае мы были бы разочарованы.
Когда Канеман выступал в ВВС Израиля с лекцией о психологии эффективного обучения, один из офицеров поделился опытом: оказывается, при перехваливании подчиненных они начинали справляться с обязанностями хуже, а вот распекание приводило к последующему более успешному исполнению приказов. Вследствие этого он перестал скупиться на «кнут» и скорее стал с осторожностью дозировать «пряники».
Канеман сразу же усмотрел в этом регрессию к среднему. Он показал офицеру, в чем тот заблуждается, продемонстрировав простое упражнение, которое вы можете опробовать на себе. Нарисовал на доске круг и предложил офицерам попасть мелком в центр этого круга, стоя при этом спиной к доске. Потом они повторили этот эксперимент, и Канеман записал, насколько результативна была первая и вторая попытка у каждого из участников.
Естественно, именно у тех, кто чрезвычайно метко попадал в круг с первого раза, вторая попытка оказывалась среди худших. Сразу же прояснилась, какая ошибка при этом происходит: изменение успешности происходит само собой. Это не означает, что обратная связь вообще не играет роли – возможно, играет, но офицер не смог привести доказательств в пользу этого.
Несовершенная корреляция и случайность
Возможно, вы уже задумываетесь, а почему же происходит регрессия к среднему, и как нам убедиться, что мы станем ее учитывать, когда она произойдет.
Чтобы понять регрессию к среднему, необходимо сначала понять корреляцию.
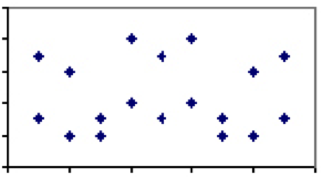
Коэффициент корреляции между двумя величинами, находящийся в диапазоне между -1 и 1 – это мера относительного веса их общих факторов. Например, если у двух явлений совсем мало общего (сравним, к примеру, потребление бутилированной воды и количество самоубийств на душу населения), то коэффициент их корреляции должен быть близок к нулю. Это означает, что, если бы мы учли все страны мира и указали на графике частоту самоубийств за конкретный год, а затем сравнили этот график с потреблением бутилированной воды на душу населения, то в полученной нами картине не было бы вообще никаких закономерностей.
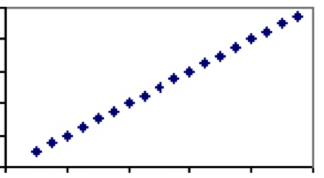
Напротив, бывают разные показатели, полностью зависящие от одного и того же фактора. Хороший пример – температура. Единственный фактор, от которого зависит температура (скорость движения молекул) прослеживается во всех масштабах, поэтому любому значению в градусах Цельсия соответствует строго определенное значение в градусах Фаренгейта. Соответственно, коэффициент корреляции между температурами по Цельсию и по Фаренгейту будет равен 1, и его график будет представлять собой прямую линию.
Но в науке найдется максимум несколько феноменов, коэффициент корреляции между которыми равен 1. При этом есть множество феноменов, между которыми прослеживается слабая или умеренная ассоциация, поэтому сравнение этих феноменов обладает некоторым объясняющим потенциалом. Рассмотрим корреляцию между ростом и весом, которая окажется где-то между 0 и 1. Практически любой трехлетка будет ниже и легче взрослого мужчины, но между трехлетками и между взрослыми мужчинами вес и рост индивидов будет отличаться.
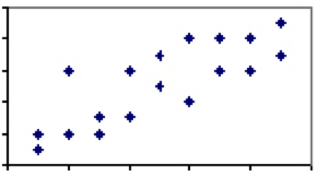
Такая вариативность и, соответственно, более низкая степень корреляции, свидетельствуют: притом, что рост – это, в целом, хороший предиктивный фактор, в образовании корреляции определенно участвуют и иные факторы кроме роста. Когда корреляция двух величин далека от идеальной, нужно следить, а не возникают ли эффекты регрессии к среднему.
Канеман вывел общее правило: Всякий раз, когда корреляция между двумя показателями несовершенна, начинается регрессия к среднему.
На первый взгляд этот вывод может смутить и показаться не слишком логичным, но степень регрессии к среднему прямо зависит от степени корреляции между переменными. Этот эффект можно проиллюстрировать на простом примере.
Допустим, вы на вечеринке спрашиваете, почему так: очень умные женщины склонны выходить замуж за партнеров, которые значительно глупее их. Большинство людей, даже те, кто хорошо подкован в статистике, быстро перейдут к поиску причинно-следственных объяснений, от избегания конкуренции к страху одиночества, который мучает таких женщин. Вероятно, настолько противоречивая тема выльется в очень активные дебаты.
А что, если теперь спросить, почему корреляция между интеллектом супругов далеко не идеальна? Этот вопрос едва ли так интересен, как первый, поскольку тут не о чем гадать – все мы знаем, что действительно не идеальна. Парадокс в том, что с алгебраической точки зрения оба этих вопроса эквивалентны. Канеман объясняет:
Если корреляция между оценками интеллекта супругов неидеальна (и если женщины и мужчины в среднем не различаются по интеллекту), то математически неизбежно, что умные женщины выйдут замуж за мужчин, которые в среднем будут менее умными (и наоборот). Наблюдаемая регрессия к среднему не может быть более интересна или более объяснима, чем неидеальная корреляция.
Предполагая, что корреляция неидеальна, вероятность встречи двух партнеров, входящих в верхний 1% по каждой из характеристик, гораздо ниже, чем встреча одного, относящегося к верхнему 1%, и другого – к нижним 99%.
Причина, следствие и что делать
Феномена регрессии к среднему следует особенно остерегаться, когда пытаешься выявить причинно-следственные связи между двумя факторами. Всякий раз при неидеальной корреляции лучшее со временем будет ухудшаться, а худшее – казалось бы, улучшаться, без какого-либо вмешательства извне. Именно этого обычно не в силах распознать не только массовые СМИ, но и подготовленные ученые.
Рассмотрим еще один пример Канемана:
Трехмесячное применение энергетических напитков для лечения депрессии у детей дает значительные улучшения состояния.
Я выдумал этот заголовок, но описанный в нем факт – правда: если какое-то время поить энергетическими напитками детей, страдающих депрессией, наблюдается клинически значимое улучшение. Аналогичным образом дети с депрессией, которые будут ежедневно по пять минут стоять на голове или по двадцать минут гладить кошек, также покажут улучшение состояния.
Большинство читателей таких заголовков автоматически заключат, что улучшение наступило из-за энергетического напитка или поглаживания кошки, но это – совершенно необоснованный вывод. Дети в депрессии – это экстремальная группа, а такие группы с течением времени регрессируют к среднему. Корреляция между уровнями депрессии во время последовательных проверок неидеальна, так что регрессия к среднему неизбежна: детям с депрессией со временем станет чуть легче, даже если они не будут гладить кошек и пить «Ред Булл».
Часто мы ошибочно усматриваем в какой-либо политике или вмешательстве причинно-следственные связи, тогда как наблюдаемые изменения относятся к экстремальной группе, и поэтому все равно бы произошли. Это приводит нас к фундаментальной проблеме: как определить, реален ли эффект, либо он объясняется простой вариативностью?
К счастью, есть способ отличить реальные улучшения от регрессии к среднему. Чтобы это сделать, вводится так называемая контрольная группа, улучшение состояния в которой, как ожидается, будет обусловлено только регрессией. Цель исследования – определить, наблюдаются ли в основной группе какие-то изменения кроме тех, которые можно объяснить простой регрессией.
В реальной жизни, где успешность конкретных индивидов или команд может сравниваться только с более ранними показателями успешности (а контрольной группы нет), абстрагировать из опыта эффекты регрессии бывает очень сложно, если не невозможно. Можно сравнивать любое значение со средним по отрасли, проводить экспертную оценку, когортное исследование или изучать темпы улучшения с исторической точки зрения, но ни один из этих показателей не является совершенным.
К счастью, сама по себе осведомленность о регрессии к среднему уже является серьезным шагом к более внимательному восприятию везения, успешности и их соотношения.
Важнейшее, чему можно научиться на примере с регрессией к среднему – это важность изучения хронологии событий, умение не поддаваться на единичные истории успеха. Надеюсь, что в следующий раз, когда вам подвернется почти идеальный образец, получившийся таким во многом благодаря удачным обстоятельствам, вы учтете, что и данный пример укладывается в регрессию к среднему, поэтому соответствующим образом скорректируете ваши ожидания.

