• Метод фазово-амплитудной интерполяции (ФАИ)
• Точное определение частоты, амплитуды и фазы гармоник сигнала
Алгоритм быстрого преобразования Фурье (БПФ) - важный инструмент для анализа и обработки сигналов различной природы.
Он позволяет реконструировать амплитудный и фазовый спектры сигнала в частотной области представления по его амплитудным отсчётам во временной, при этом метод вычислительно оптимизированный при скромном расходе памяти.
Хотя в процессе преобразования никакая информация о сигнале не утрачивается (вычисления обратимы до округлений) алгоритму присущи некоторые особенности:
разрешающая способность, своего рода, "дискретная пикселизация" наподобие гистограммы
эффект спектральной утечки, обуславливающий характерное растекание информации по столбикам гистограммы для тех гармоник сигнала, частота которых не попадает весьма точно на деления дискретной частотной решётки
Эти факторы затрудняют высокоточный анализ и тонкую обработку результатов в дальнейшем.

В статье представлен действенный способ преодоления таких "неудобных" особенностей алгоритма.
Материалы снабжены иллюстрациями, однако для более глубокого погружения в тему рекомендуется скачать десктоп-приложение Solfeggio для высокоточной обработки и визуализации сигналов. С его помощью можно в деталях рассмотреть сигнал и "прощупать" его спектры на различных уровнях масштаба: от общей картинки вплоть до отдельных дискретных отсчётов.
ВАЖНО! Программа и алгоритмические наработки бесплатны для учебного и некоммерческого использования, однако есть ряд важных ограничений на области применения. Пожалуйста, перед внедрением представленных наработок в какие-либо проекты внимательно прочтите небольшое соглашение...
Именно в процессе создания Solfeggio были выявлены закономерности, которые в результате привели к разработке алгоритма фазово-амплитудной интерполяции для быстрого преобразования фурье (ФАИ для БПФ). При этом были сформулированы нерешённые задачи.
Теперь кратко пройдёмся по основным этапам и положениям теории обработки сигналов:
приёмник (микрофон или иной датчик) улавливает аналоговый сигнал и преобразует его в эквивалентные колебания напряжения электрического тока
аналогово-цифровой преобразователь (АЦП) с заданной частотой (то есть через равные интервалы времени) измеряет уровень напряжения входного сигнала и формирует массив (кадр) его временнЫх дискретных отсчётов, квантованных по уровню амплитуды
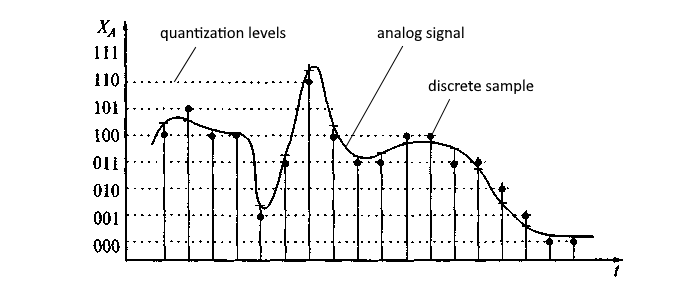
затем на основе сформированного кадра выполняется вычисление прямого БПФ, в результате которого на выходе получается массив спектральных данных, который даёт некоторое представление о гармониках исходного аналогового сигнала (амплитудах и фазах доминирующих частот), что с определённой погрешностью позволяет реконструировать свойства исходного аналогового сигнала (см. рис. 1)
Как упоминалось ранее, поскольку спектральное представление является дискретным, а не аналоговым, ему присуща разрешающая способность, своего рода, пикселизация наподобие столбиков гистограммы, а также может наблюдаться спектральная утечка, которая обуславливает характерное растекание информации о гармониках сигнала, частота которых не попадает довольно точно в деления дискретной частотной решётки. Эти явления на практике затрудняют последующую реконструкцию и анализ исходных сигналов.
Важно отметить, что применение обратного БПФ к полученному массиву спектральных данных позволяет однозначно восстановить исходный дискретный сигнал во временной области (с точностью до округлений), что указывает на то, что в процессе преобразования никакая информация из сигнала не утрачивается. Это означает, что вычисления обратимы.
В свою очередь согласно теореме Найквиста-Шеннона-Котельникова аналоговый сигнал может быть однозначно и без искажений восстановлен по своим дискретным временным отсчётам, когда частота дискретизации как минимум в два раза превышает частоту наиболее высокочастотной гармоники сигнала. Это наводит на мысль, что, интерполировав дискретный сигнал во временной области (обратно превратив в аналоговый) и повысив частоту дискретизации (повторно передискретизировав), можно достичь более высокого разрешения в фазо-частотной области представления за счёт увеличения вычислительной сложности и повышения потребления памяти. Этот подход применим, однако не всегда удобен на практике.
ЗАГАДКА №1
Но раз возможна интерполяция сигнала во временной области представления, может быть, существует какой-то метод интерполяции в частотной? Хотя на момент написания статьи математического обоснования этой гипотезе нет, экспериментальные данные указывают на то, что для малозашумленных сигналов подобный подход существует, и для многих распространённых практических ситуаций даёт он весьма точные и надёжные результаты.
ЗАГАДКА №2
Хотя точность метода высока, однако и ему присуща некоторая погрешность. Возможно, эту погрешность можно снизить, уточнив формулы. Вопрос также остаётся открытым.
Метод интерполяции интуитивен и на удивление вычислительно прост. Он был экспериментально обнаружен во время разработки программы-инструмента Solfeggio для высокоточного спектрального анализа.
Итак, сначала рассмотрим классический алгоритм быстрого преобразования Фурье на языке C#. Ниже представлены две модификации операции "бабочка" (с прореживанием по времени и по частоте), которые различаются порядком и структурой циклов, но в итоге ведут к одному результату
private static void DecimationInFrequency(ref Complex[] sample, bool direct)
{
if (sample.Length < 2) return;
var length = sample.Length / 2; // sample.Length >> 1
var sampleA = new Complex[length];
var sampleB = new Complex[length];
var abs = (Pi.Single / length).InvertSign(direct);
var rotorBase = new Complex(Cos(abs), Sin(abs));
var rotor = Complex.One; // rotor = rotorBase.Pow(0)
for (int i = 0, j = length; i < length; i++, j++)
{
var a = sample[i];
var b = sample[j];
sampleA[i] = a + b;
sampleB[i] = (a - b) * rotor;
rotor *= rotorBase; // rotor = rotorBase.Pow(i + 1)
}
DecimationInFrequency(ref sampleA, direct);
DecimationInFrequency(ref sampleB, direct);
for (int i = 0, j = 0; i < length; i++) // j += 2
{
sample[j++] = sampleA[i];
sample[j++] = sampleB[i];
}
}
private static void DecimationInTime(ref Complex[] sample, bool direct)
{
if (sample.Length < 2) return;
var length = sample.Length / 2; // sample.Length >> 1
var sampleA = new Complex[length];
var sampleB = new Complex[length];
var abs = (Pi.Single / length).InvertSign(direct);
var rotorBase = new Complex(Cos(abs), Sin(abs));
var rotor = Complex.One; // rotor = rotorBase.Pow(0)
for (int i = 0, j = 0; i < length; i++) // j+=2
{
sampleA[i] = sample[j++];
sampleB[i] = sample[j++];
}
DecimationInTime(ref sampleA, direct);
DecimationInTime(ref sampleB, direct);
for (int i = 0, j = length; i < length; i++, j++)
{
var a = sampleA[i];
var b = sampleB[i] * rotor;
sample[i] = a + b;
sample[j] = a - b;
rotor *= rotorBase; // rotor = rotorBase.Pow(i + 1)
}
}
Нормализация значений после операции "бабочка" выполняется следующим образом
public static partial class Butterfly
{
public static Complex[] Transform(this IEnumerable<Complex> sample, bool direct, bool inTime = false)
{
var workSample = sample.ToArray();
if (inTime) DecimationInTime(ref workSample, direct);
else DecimationInFrequency(ref workSample, direct);
double factor = direct ? workSample.Length / 2 : 2;
for (var i = 0; i < workSample.Length; i++) workSample[i] /= factor;
return workSample;
}
}
Метод фазово-амплитудной интерполяции (ФАИ)
Теперь рассмотрим метод фазово-амплитудной интерполяции (ФАИ).
public static IEnumerable<Bin> Interpolate(this IList<Bin> spectrum, List<int> resonances = default)
{
resonances?.Clear();
var count = spectrum.Count / 2 - 4;
for (var i = 0; i < count; i++)
{
/* Frequency (F); Magnitude (M); Phase (P); */
spectrum[i + 0].Deconstruct(out var aF, out var aM, out var aP);
spectrum[i + 1].Deconstruct(out var bF, out var bM, out var bP);
spectrum[i + 2].Deconstruct(out var cF, out var cM, out var cP);
spectrum[i + 3].Deconstruct(out var dF, out var dM, out var dP);
double GetPeakProbabilityByPhase() => Math.Abs(cP - bP) / Pi.Single;
double GetPeakProbabilityByMagnitude()
{
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
return
(aM < bcM && bcM > dM)
&&
(bM * 0.95 < bcM && bcM > cM * 0.95)
? 0.95
: 0.05;
}
var peakProbabilityByPhase = GetPeakProbabilityByPhase();
var peakProbabilityByMagnitude = GetPeakProbabilityByMagnitude();
var peakProbability = peakProbabilityByPhase * peakProbabilityByMagnitude;
if (peakProbabilityByMagnitude > 0.5 && peakProbabilityByPhase < 0.5)
resonances?.Add(i);
if (peakProbability > 0.5)
{
/*
var halfStepF = (cF - bF) / 2;
var bcMiddleF = (bF + cF) / 2;
var bcOffsetScale = (cM - bM) / (cM + bM);
var bcF = bcMiddleF + bcOffsetScale * halfStepF;
*/
var bcF = (bF * bM + cF * cM) / (bM + cM);
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
var bcP = bP + (bcF - bF) * (cP - bP) / (cF - bF);
/* y(x) = y0 + ( x - x0) * (y1 - y0) / (x1 - x0) */
var abF = aF + (bcF - bF);
var abM = aM;
var abP = aP;
var dcF = dF + (bcF - cF);
var dcM = dM;
var dcP = dP;
yield return new(in abF, in abM, in abP);
yield return new(in bcF, in bcM, in bcP);
yield return new(in dcF, in dcM, in dcP);
i += 3;
}
else
{
yield return new(in aF, in aM, in aP);
}
}
}
Точное определение частоты, амплитуды и фазы гармоник сигнала
Ключевыми являются три строчки
var bcF = (bF * bM + cF * cM) / (bM + cM);
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
var bcP = bP + (bcF - bF) * (cP - bP) / (cF - bF);
/* y(x) = y0 + ( x - x0) * (y1 - y0) / (x1 - x0) */
Именно по этим формулам с довольно высокой точностью вычисляется частота, амплитуда и фаза размытой по спектру гармоники. Первая и треться формулы для частоты и фазы выведены интуитивно, вторая для амплитуды подобрана экспериментальным путём. На момент написания статьи строго математического обоснования этим формулам не найдено.
Примечательно, что представленные формулы наилучшим образом работают для прямоугольного окна, то есть не требуют дополнительной предобработки дискретного кадра. Применение каких-либо других оконных функций лишь снижает их точность.
Наличие нескольких близлежащих гармоник в спектре может вносить дополнительные искажения в точность интерполяции, но для отдалённых друг от друга гармоник погрешности снижаются к минимуму.
Из каких наблюдений получены формулы?
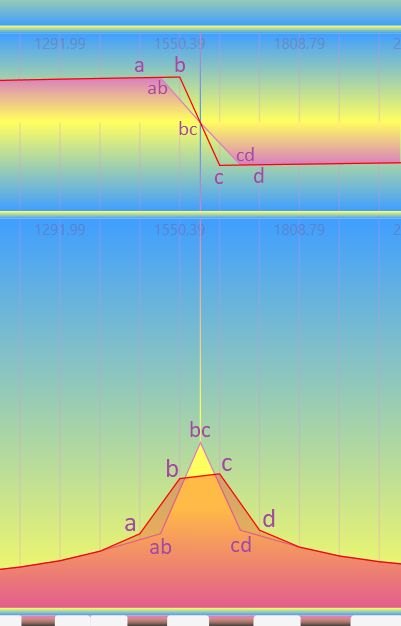
Рассмотрим амплитудный и фазовый спектры единичной гармоники при попадании частоты на деление дискретной решётки, а также в разные части интервала между двумя близлежащими делениями.
Частоту i-того деления решётки можно рассчитать по следующей формуле
var binToFrequency = sampleRate / frameSize;
var binFrequency = i * binToFrequency;
При попадании гармоники в деление решётки на амплитудном спектре наблюдается чёткий пик, а эффект спектрального размытия отсутствует, значёния амплитуд на остальных делениях близки к нулевым. Значение фазы также определяются с высокой точностью, однако на фазовом спектре начинают наблюдаться резкие фазовые скачки.
При лёгком сдвиге частоты в интервал между двумя делениями решётки на амплитудном спектре начинает проявляться эффект утечки и характерный срез пика у гармоники, который достигает своего максимума на средине интервала. При этом интересная картина наблюдается на фазовом спектре: значение фазы гармоники теперь лежит на прямой, которая соединяет значения на двух близлежащих делениях решётки, а остальная часть фазового спектра образует гладкие кривые.

Внимательное рассмотрение процесса сдвига раскрывает следующую закономерность
var halfStepF = (cF - bF) / 2;
var bcMiddleF = (bF + cF) / 2;
var bcOffsetScale = (cM - bM) / (cM + bM);
var bcF = bcMiddleF + bcOffsetScale * halfStepF;
Выполнение подстановок и преобразований с упрощениями приводит к следующим выражениям для расчёта точной частоты гармоники и её фазы
var bcF = (bF * bM + cF * cM) / (bM + cM);
var bcP = bP + (bcF - bF) * (cP - bP) / (cF - bF);
/* y(x) = y0 + ( x - x0) * (y1 - y0) / (x1 - x0) */Значение амплитуды угадать немного сложнее, но с достаточно высокой точность оно описывается выражением
var bcM = (bM + cM) - (aM + dM) / Pi.Half;Необходимо упомянуть методы выявления размытых пиков в сигнале для их дальнейшей интерполяции. Существует два характерных признака по которым можно определить кандидата: срезанный пик на амплитудном спектре и скачок на фазовом. Но более надёжным является комбинированный вероятностный подход.
double GetPeakProbabilityByPhase() => Math.Abs(cP - bP) / Pi.Single;
double GetPeakProbabilityByMagnitude()
{
var bcM = (bM + cM) - (aM + dM) / Pi.Half;
return
(aM < bcM && bcM > dM)
&&
(bM * 0.95 < bcM && bcM > cM * 0.95)
? 0.95
: 0.05;
}
var peakProbabilityByPhase = GetPeakProbabilityByPhase();
var peakProbabilityByMagnitude = GetPeakProbabilityByMagnitude();
var peakProbability = peakProbabilityByPhase * peakProbabilityByMagnitude;
if (peakProbabilityByMagnitude > 0.5 && peakProbabilityByPhase < 0.5)
resonances?.Add(i);
if (peakProbability > 0.5)Выявление резонансов
Следует отметить, что характерные амплитудные срезы могут также возникать при резонансах, когда две или более значимые гармоники лежат в одном или близлежащих интервалах дискретной решётки, но в таком случае на фазовом спектре начинает возникать эффект слияния двух скачков, что позволяет отличить резонанс от явления спектральной утечки.
В общем случае резонирующими являются две любые гармоники, просто характерный эффект биений начинает становится наиболее заметным, когда их частоты достаточно близки.

ЗАГАДКА №3
Интересное наблюдение: резонанс очень напоминает амплитудную модуляцию низкочастотного сигнала высокочастотным, например, резонанс 440 и 444 герц похож на 4 герцевый сигнал (или частоты такого порядка), модулированной частотой примерно в 442 герца. Данное предположение требует исследования, уточнений и дальнейшей проверки.
На заключительном этапе, после выполнения ФАИ, из спектральных данных легко выделить чистые гармонические составляющие, которые уже имеют не попиксельное, а растровое представление (частота/амплитуда/фаза).
public static IEnumerable<Bin> EnumeratePeaks(this IList<Bin> spectrum, double silenceThreshold = 0.01)
{
var count = spectrum.Count / 2 - 3;
for (var i = 0; i < count; i++)
{
spectrum[i + 0].Deconstruct(out var aF, out var aM, out var aP);
spectrum[i + 1].Deconstruct(out var bF, out var bM, out var bP);
spectrum[i + 2].Deconstruct(out var cF, out var cM, out var cP);
if ((aM + cM) * 0.25d < bM && aM < bM && bM > cM && bM > silenceThreshold)
yield return spectrum[i + 1];
}
}Метод позволяет выявить набор наиболее выраженных гармоник исходного сигнала, после чего их легко представить в виде комплексных чисел либо косинусоид для дальнейшей высокоточной обработки с помощью базовых математических операций.
В некоторых случаях это обеспечивает ощутимое информационное сжатие сигналов за счёт потери малозначимых и шумовых гармоник, благодаря чему можно производить дальнейшие вычисления и преобразования более компактно и оптимально, чем при работе с исходными растровыми массивами.
ИТОГИ
Метод фазово-амплитудной интерполяции открывает новые возможности в области обработки и сжатия сигналов, поскольку позволяет из дискретно-растрового представления сигнала выделить с высокой точностью его аналого-векторную информационную составляющую.
ЗЕРКАЛА СТАТЬИ
EN: makeloft, gitlab, gihub, habr
RU: makeloft, gitlab, gihub, habr
ПЕСОЧНИЦА
Комментарии (58)

maxkomp
28.03.2022 09:56+5Чтобы частотные пики гармоник сигнала, которым не повезло угодить точно в сетку частот БПФ, не "растекались" по соседним линиям спектра, обычно применяют различные оконные функции. Их придумали в ассортименте: Хемминга, Ханнига, Блекмана, и т.д.
Какую именно функцию лучше использовать - зависит от того, что у вас за сигнал и что вы хотите из него добиться. Одно дело - нарисовать красивую картинку для качественной оценки. Совсем другое - выполнить какие-то измерения и получить по возможности точные результаты, имея оцифрованный сигнал в качестве исходных данных.
Исследование близко расположенных частотных составляющих в сигнале. То, что в статье называется "резонанс". Я бы это назвал не резонансом, а биениями, но не суть. Их можно исследовать, просто увеличивая длительность оцифрованного сигнала. Чем длиннее выборка, тем лучше разрешение в частотной области у преобразования Фурье. Хотите исследовать гармоники сигнала с точностью до 0.001 Гц? Оцифровывайте его в течение 1000 сек, и будет вам счастье. Правда, тут все хорошо в меру. Если вы увеличите длину выборки до миллионов и миллиардов сэмплов, то БПФ уже даст неприятные погрешности.
Чтобы этого не случилось, можно применить такой вычислительный трюк, как "растяжка спектра" (поиск в гугле по словам zoom FFT). Продолжительность вашей выборки (в секундах) он уменьшить не позволит, (в примере выше - записывать сигнал на протяжении 1000 сек все равно придется), но размеры выборки (в сэмплах) сократятся до вполне вменяемых величин. Рекомендую попробовать.
Из трюков и фокусов, связанных с исследовпнием биений, можно упомянуть еще преобразование Гильберта. (При определенных условиях и предположениях его можно использовать для разделения модулированного по амплитуде сигнала, на несущую и огибающую). А биения - это, по сути, и есть амплитудная модуляция. И преобразование Гильберта в данных условиях неплохо работает.

Makeman Автор
28.03.2022 10:28Благодарю за интерес к статье и рекомендации!
ФАИ обеспечивает более высокую точность при прямоугольном окне, чем применение каких-либо других оконных функций.
Качественные результаты получаются не только на сгенерированных идеальных сигналах, но и вполне реальных, например, аудиосигнале с микрофона. Как минимум, по частоте обеспечивается точность гитарных тюнеров при сопоставимых размерах окна.

Andy_U
28.03.2022 10:22+4Автор постоянно упоминает БПФ, но это лишь способ быстрого вычисления коэффициентов дискретного преобразования Фурье. Ну и любые попытки восстановить частоты и/или значения сигнала в промежуточных точках - это попытка высосать информацию из пальца.

Makeman Автор
28.03.2022 10:43Спасибо за интерес к статье!
Возможно, вы пока что не вполне уловили её суть... Рекомендую скачать приложение Solfeggio и сравнить результаты на идеальных и реальных сигналах (например, с микрофона) в результате чистого БПФ и связки БПФ+ФАИ.

Andy_U
28.03.2022 11:19+3Возможно, вы пока что не вполне уловили её суть...
С каким из двух моих утверждений вы не согласны?

Makeman Автор
28.03.2022 11:36Со вторым
Ну и любые попытки восстановить частоты и/или значения сигнала в промежуточных точках - это попытка высосать информацию из пальца.
Это утверждение отчасти может быть верно для белого шума, но не для разрежённых сигналов с чёткими или растёкшимися в результате выполнения БПФ амплитудными пиками.

Andy_U
28.03.2022 12:28+2Это утверждение отчасти может быть верно для белого шума
Т.е. вы утверждаете, что иногда мое утверждение неверно для белого шума? Поскольку у вашей статьи есть тег "Математика", я бы с удовольствием увидел математически корректное доказательство вашего утверждения ;)
но не для разрежённых сигналов с чёткими или растёкшимися в результате выполнения БПФ амплитудными пиками.
Вы понимаете, что чисто гармонический сигнал (Фурье интеграл - дельта-функция) - это когда синусоида с постоянной амплитудой в произвольный момент времени от минус до плюс бесконечность?

Makeman Автор
28.03.2022 12:48Не берусь ничего утверждать, но, возможно, ваше утверждение категорически верно для идеального белого шума, но в остальных случаях лишь отчасти, с определённой долей вероятности и погрешности.
У меня прикладной взгляд в данном вопросе - этот алгоритм с высокой точностью работает на реальных сигналах, даже если кто-то говорит, что это невозможно ;)
Всем скептикам рекомендую скачать приложение и воочию протестировать ФАИ на реальных сигналах.
Исходные коды полностью открыты, можно удостовериться, что больше никакой дополнительной обработки к сигналам не применяется.

Andy_U
29.03.2022 00:05+2Всем скептикам рекомендую скачать приложение и воочию протестировать ФАИ на реальных сигналах.
Исходные коды полностью открыты, можно удостовериться, что больше никакой дополнительной обработки к сигналам не применяется.
Вы извините, но восстанавливать математический алгоритм по коду я не буду. И использовать код, который непонятно как работает (или врет) тоже не буду. Еще раз напомню, что это вы поставили тег "математика". Где она? А на нет и суда нет. Ну если хотя бы то была библиотека на C++ или пакет на Питоне, чтобы можно было нормально протестировать так чтобы глаза не вытекли....

Makeman Автор
29.03.2022 09:22Дело ваше. Там всего-то небольшой метод и три ключевых формулы.
Для меня программирование - это часть математики, вычисления, которые можно выполнять на компьютере.

Refridgerator
29.03.2022 07:34Ну и любые попытки восстановить частоты и/или значения сигнала в промежуточных точках — это попытка высосать информацию из пальца.
Это не так, теорема Котельникова как раз и рассматривает однозначное восстановление непрерывного сигнала из набора дискретных отсчётов.
Andy_U
29.03.2022 09:03Тут конечное число отсчетов и еще нет ограниченного спектра.

Refridgerator
29.03.2022 09:23Спектр ограничен по определению (осуществляется фильтром низких частот непосредственно в самом АЦП), а из конечного числа отсчётов при ДПФ следует лишь их цикличность.

Andy_U
29.03.2022 09:31Первое - лишь приблизительно, Второе - где цикличность у затухающего сигнала?

Refridgerator
29.03.2022 09:55Первое — с чего это вдруг? Второе — цикличность не у самого исходного сигнала, а у мат. аппарата, его рассматривающего — точно там же, где цикличность суммы конечного числа синусоид с кратными частотами. Достаточно вычислить обратное ДПФ аналитически, а не численно, чтобы убедиться в этом.

Andy_U
29.03.2022 10:08Первое — с чего это вдруг?
Я с удовольствием увижу физически реализуемый фильтр, убивающий 100% частот, выше заданной.
Второе — цикличность не у самого исходного сигнала, а у мат. аппарата, его рассматривающего — точно там же, где цикличность суммы конечного числа синусоид с кратными частотами. Достаточно вычислить обратное ДПФ аналитически, а не численно, чтобы убедиться в этом.
Так, давайте на конкретном примере. Пусть мы измерили сигнал 4 раза:
t=0, x=0
t=1, x=1
t=2, x=2
t=3 x=3
Чему будет равен сигнал при t=4? А при t=1.5? А ведь это еще без шума тракта и шума дискретизации.

Refridgerator
29.03.2022 11:23Я с удовольствием увижу физически реализуемый фильтр, убивающий 100% частот, выше заданной.
А 100% и не надо, достаточно ниже шумов квантования и прочих, потому что при всём желании вы не можете численно работать с неограниченной точностью. Ну и при любом раскладе в физическом мире верхняя частота любого сигнала ограничена скоростью света.Так, давайте на конкретном примере. Чему будет равен сигнал при t=4? А при t=1.5?
Вы в этом примере очень хитро подменили реальный сигнал и его мат.модель — предсказывать будущее ещё никто не научился.
Ну а в мат.модели — если вы уверены, что все прочие х равны нулю, а сигнал удовлетворяет требованиям Котельникова — то:
Ну или вы знаете, что все прочие x равны -1:
Ну или вы знаете, что сигнал периодичен и точно знаете период — то например:
Подставляйте интересующее вас x в функцию, получите конкретное значение.
Andy_U
29.03.2022 12:19А 100% и не надо, достаточно ниже шумов квантования и прочих, потому что при всём желании вы не можете численно работать с неограниченной точностью. Ну и при любом раскладе в физическом мире верхняя частота любого сигнала ограничена скоростью света.
Вы представляете сложность даже такого фильтра? Ну а если я хочу смотреть на нефильтрованный сигнал? Есть померянные с некоторой точностью отсчеты, а между ними - неизвестность. Хотите точнее - собирайте больше данных. Чаще, дольше. Та же ситуация, что и в мат.статистике.
Вы в этом примере очень хитро подменили реальный сигнал и его мат.модель — предсказывать будущее ещё никто не научился.
Я там и про t=1.5 спросил. И по Вашим графикам (Mathematica?) видно, что при разных предположениях о сигнале, даже при ограниченном спектре, в промежуточных точках получаются разные предсказания. Также видно, что идеальная фильтрация сильно искажает форму сигнала x(t)=t.

Refridgerator
29.03.2022 12:58что при разных предположениях о сигнале
Ну это логично, а как иначе-то? Если брать сигнал с магнитофона после кнопки «Вкл.» и до кнопки «Выкл.», то вполне логично дополнять его нулями (то бишь тишиной) с обоих сторон. Если у микрофона мембрана физически не в состоянии реагировать на частоты выше определённой — то вполне логично считать сигнал с него спектрально ограниченным.Также видно, что идеальная фильтрация сильно искажает форму сигнала x(t)=t
Очевидно что сигнал с бесконечным спектром под критерии Котельникова не подходит, и для работы с таким сигналами используются другие мат.модели и другие инструменты. Равно как и в реальном физическом мире вы такой сигнал ничем воспроизвести не сможете — из-за физических ограничений элементной базы.
Andy_U
29.03.2022 13:13Ну это логично, а как иначе-то?
Я же не спорю, это автор пытается добыть из данных дополнительную информацию, изначально там отсутствующую.

Makeman Автор
29.03.2022 22:24Ничего автор не добывает.
Алгоритм в результате наоборот убирает избыточную и малозначимую информацию, с довольно высокой точностью реконструируя идеальный сигнал.
На сильно зашумленных сигналах он, конечно, чудес не сотворит, но с реальными (музыка, речь) справляется достойно.

Andy_U
29.03.2022 22:44+1У вас при обратном Фурье-преобразовании значения в исходных точках восстанавливаются точно?

Makeman Автор
30.03.2022 01:08В заключительной части статьи добавлен раздел "песочница", который содержит ссылку на реализацию алгоритма в онлайн-компиляторе. Там можно самому поиграть с данными и получить непосредственное представление, какая информация теряется, а какая восстанавливается, и насколько точно.

FGV
28.03.2022 10:36+1А что мешает выполнить преобразование Фурье не для дискретного набора частот (как в БПФ) а для нужного набора частот (скажем от 0 до fs/2 с шагом df)?

Makeman Автор
28.03.2022 10:59Вычислительная сложность. БПФ значительно сокращает объёмы вычислений и расходы памяти (то есть обладает наименьшей избыточностью по данным показателям, чем другие методы вычисления преобразования Фурье), при этом обеспечивая обратимость преобразования (возможность однозначного восстановления исходного сигнала до точности округлений).
В теории можно рассчитать коэффициенты преобразования Фурье с огромной точностью, но для этого потребуется много вычислительных ресурсов, что накладывает серьёзные ограничения на их вычисление в режиме реального времени.

maxkomp
28.03.2022 11:51+4Тут основное ограничение - на длину выборки сигнала.
Дискретное преобразование Фурье устроено так, что если мы хотим исследовать в подробностях составляющую сигнала с частотой f, то в нашей выборке обязано находиться целое количество периодов такого сигнала, который имеет частоту f.
Второе ограничение связано с БПФ.
БПФ - это, по сути, хитрый вычислительный трюк, который позволяет очень быстро выполнить дискретное преобразование Фурье, при выполнении очень мааааленького дополнительного ограничения: длина выборки сигнала обязана быть степенью числа 2. Но зато преобразование выполнится ну ооочень быстро.
То есть если выборка у нас получилась длиной 1024 смп, то все отлично, вычисляем спектр за сущие микросекунды. А если (не дай бог) для того, чтобы исследовать в подробностях интересующую вас в сигнале частоту f , приходится брать выборку в 1025 или в 1023 смп, то происходит страшное... Бпф не работает, и для вычисления такого же спектра требуется в десятки раз больше времени.
Значит, способов решения проблемы тут два.
подобрать частоту квантования АЦП так, чтобы нужная частота сигнала уложилась в подходящее для бпф количество сэмплов. Это не всегда удобно и не всегда возможно технически.
Использовать БПФ только для получения общей картины спектра сигнала. А для подробного и детального исследования его составляющих лучше применять ДПФ. Да, это конечно, будет медленно. Но вам ведь не нужно вычислять все коэфф Фурье, весь их полный набор для вашей выборки сигнала! Достаточно вычислить только один единственный коэффициэнт, который соответствует интересующей вас сейчас частоте f. Или набору частот (их все равно будет сильно меньше, чем длина выборки) Для современных компьютеров - вполне посильная задача. Тогда и не придется умничать с интерполяциями. С точки зрения математики, интерполяция, экстраполяция - это, по сути, игра в угадайку. Иногда это может сработать и вы угадаете подходящее значение (если окажутся верны исходные предположения о сигнале). А может так случиться, что и не угадаете.

Makeman Автор
28.03.2022 12:16Если изначально выборка удовлетворяет теореме Найквиста-Шеннона-Котельникова, то её длину можно искусственно варьировать, интерполируя сигнал во временной области и выполняя передискретизацию с большей частотой, что будет приводить к возрастанию спектрального разрешения за счёт увеличения объёмов вычислений и потребления памяти.
Преимущество ФАИ в том, что алгоритм позволяет весьма точно «угадать» характеристики сразу нескольких достаточно отдалённых гармоник сигнала при малом объёме дополнительных вычислений.
Другими словами, ФАИ - это метод высокоточного сжатия разрежённых сигналов с минимальными потерями полезной информации.

diakin
31.03.2022 00:21передискретизацию с большей частотой, что будет приводить к возрастанию спектрального разрешения
Ну, вообще, для увеличения спектрального разрешения надо увеличивать длительность выборки. Увеличением частоты дискретизации можно расширить спектр в область высоких частот.
А так да, можно вырезать из выборки кусок, чтобы туда укладывалось целое число периодов сигнала, а потом передискретизировать\интерполировать число точек к ближайшей степени двойки.

Andy_U
28.03.2022 12:30БПФ - это, по сути, хитрый вычислительный трюк, который позволяет очень длина выборки сигнала обязана быть степенью числа 2. Но зато преобразование выполнится ну ооочень быстро.
Не-не. Главное, чтобы не простое. Но, да, чем лучше факторизуется, тем быстрее.
Вдогонку, можно даже и простое: https://en.wikipedia.org/wiki/Fast_Fourier_transform

Refridgerator
29.03.2022 07:23А если (не дай бог) для того, чтобы исследовать в подробностях интересующую вас в сигнале частоту f, приходится брать выборку в 1025 или в 1023 смп, то происходит страшное…
Ничего страшного не происходит, для этого есть prime-factor и Bluestein алгоритмы. Они просто сложнее в реализации, Bluestein дополнительно требует увеличения точности для больших n (>50000).

Biga
28.03.2022 12:56+3Частоту сигнала намного точнее можно вычислять при помощи автокорреляции (тоже через БПФ). Пик автокорреляции даст период с точностью до нескольких отсчётов, а уж период в частоту перевести легко. Результат получается на порядки точнее, чем по спектру, особенно для низких частот. Собственно, чем ниже частота, тем выше точность по автокорреляции и ниже по спектру. Если, к примеру, писать программу-тюнер для гитары, то я бы советовал использовать автокорреляцию.
Есть и подводные камни:
Нужно использовать дополнительные эвристики для отсеивания пиков на гармониках.
Для смешанного сигнала (несколько частот) понадобится сначала отделить нужную частоту при помощи фильтра частот.(Без претензий к ТС, просто вдруг кому-то пригодится.)

Makeman Автор
28.03.2022 13:07Спасибо за отклик и интерес к статье!
Даже на низких частотах ФАИ обеспечивает точность сравнимую с автокорреляционными музыкальными тюнерами при эквивалентных длинах выборки (сам проверял). Возможно, какая-то разница будет наблюдаться на сверхнизких частотах, но это требует дальнейшей проверки и исследования.

Refridgerator
29.03.2022 06:20+2может быть, существует какой-то метод интерполяции в частотной? Хотя на момент написания статьи математического обоснования этой гипотезе нет
Существует уже почти 100 лет — читайте про sinc и periodic-sinc функции, алгоритмы передискретизации, ну и вообще любой доступный учебник по обработке сигналов.Интересное наблюдение: резонанс очень напоминает амплитудную модуляцию низкочастотного сигнала высокочастотным, например, резонанс 440 и 444 герц похож на 4 герцевый сигнал (или частоты такого порядка), модулированной частотой примерно в 442 герца. Данное предположение требует исследования, уточнений и дальнейшей проверки.
Данное предположение описывается и доказывается в школьном курсе тригонометрии (разложение произведения синусов на сумму и наоборот).

Makeman Автор
29.03.2022 09:14Спасибо за интерес к статье!
Не знаю, в какой области работают sinc и periodic-sinc функции, но алгоритмы передискретизации точно работают во временной (применяются к исходной выборке), речь же идёт про алгоритм интерполяции в частотной области (применяется к спектру после БПФ).

Refridgerator
29.03.2022 09:45+1Я прекрасно понял, о чём идёт речь в вашей статье. Временная и частотная область однозначно соотносятся друг с другом — в частности, свёртка во временной области равносильна умножению в частотной и наоборот, взятие производной во временной области равносильна умножению на i·w в частотной и наоборот, и так далее. Алгоритмы передискретизации точно также применимы и там и там, и описаны могут быть и там и там, и к интерполяции имеют непосредственное отношение. И собственно сама рассматриваемая вами задача тоже далеко не новая и тоже давно решена всеми возможными способами (спойлер: ваш вариант далеко не лучший).

Andy_U
29.03.2022 10:34Я почему хотел увидеть алгоритм автора статьи, чтобы хотя бы убедиться, что при обратном преобразовании сигнал остался неизменным или хотя бы вещественным.

Refridgerator
29.03.2022 12:00Чтобы не переживать по поводу мнимой составляющей — можно использовать преобразование Хартли, у которого и вход, и выход строго вещественные, и которое можно получить напрямую из преобразования Фурье просто сложением действительной и мнимой составляющей. Он мало известен просто потому, что с комплексными числами проще работать, а также потому, что алгоритм быстрого дискретного преобразования Хартли был запатентован его создателем (сейчас срок этого патента уже истёк). А пока он был в силе, придумали кучу других алгоритмов под общим названием Real FFT, которые при преобразовании учитывают симметрию Эрмита (Hermitian symmetry).
Ну а поскольку восстановление исходного сигнала в задачи автора не входило, то это у него и не получится.
Makeman Автор
29.03.2022 12:27Ну а поскольку восстановление исходного сигнала в задачи автора не входило, то это у него и не получится.
Сигналы с разрежёнными гармониками вроде звуковых восстанавливаются с довольно высокой точностью, при этом происходит очистка от шумов (малозначимых гармоник).
Да, это неоднозначное восстановление с потерями, но и преимущество для определённых задач.

Andy_U
29.03.2022 12:33Так автор только сейчас (см.ниже) свою весьма специфическую цель обозначил. А, то, скачайте, попробуйте...

Makeman Автор
29.03.2022 12:01Алгоритм представлен в статье. С разрежёнными гармониками в идеальных и реальных сигналах он справляется очень даже неплохо.

Andy_U
29.03.2022 12:31Вы бы его еще на brainfack'е написали :)

Makeman Автор
29.03.2022 22:10Но... Чем вам C# не угодил? Это современнный (не побоюсь этого слова, передовой) язык программирования широкого предназначения. Синтаксически близок к Java, во многих аспектах опережает её, также есть немало общих черт с C++.
Да и алгоритм не настолько сложен (по сути, около десятка формул), чтобы даже интуитивно при внимательном рассмотрении с ним не разобраться. Если же есть какие-то затруднения или вопросы, то можно спросить, уточнить...
:)

Andy_U
29.03.2022 22:37Я хотел бы только заметить, что тот мой комментарий, где я в первый раз отказался восстанавливать алгоритм из кода, понравился еще двум читателям. Т.е. или нам троим заниматься reverse engineering'ом, или вам эти формулы опубликовать. Или у вас их нет, а есть только код?

Makeman Автор
29.03.2022 12:12Лучший и худший - понятия довольно относительные, которые зависят от критериев оценки.
Первоочередная цель при создании приложения Solfeggio - точное распознавание нот из звуковых сигналов в режиме реального времени. С этой задачей ФАИ справляется на уровне автокорреляционных тюнеров для музыкальных инструментов, при этом в вычислительном плане метод не требователен к ресурсам.
Возможно, существуют ещё более совершенные подходы для решения подобного рода задач, но мне они не известны.

Refridgerator
29.03.2022 13:12+2Первоочередная цель при создании приложения Solfeggio — точное распознавание нот из звуковых сигналов в режиме реального времени. С этой задачей ФАИ справляется на уровне автокорреляционных тюнеров для музыкальных инструментов
Вот именно, что «распознавание нот» и «тюнер для музыкальных инструментов» — это совершенно разные задачи, и в обоих случаях есть более совершенные в плане точности алгоритмы, в том числе и без FFT вообще. FFT даёт линейную шкалу частот, в то время как распределение частот в нотах логарифмическое. Для распознавания нот банк узкополосных фильтров с выделением огибающей через преобразование Гильберта будет точнее.
Makeman Автор
29.03.2022 21:58Для распознавания нот банк узкополосных фильтров с выделением огибающей через преобразование Гильберта будет точнее.
Большой вопрос к вычислительной сложножности данного подхода... А точность можно существенно повысить и для БПФ, опять же за счёт повышения требований к вычислительным ресурсам.
«распознавание нот» и «тюнер для музыкальных инструментов» — это совершенно разные задачи
Тюнер - это точное распознование одной наиболее значимой ноты в сигнале, то есть частный случай более общей задачи по точному распознованию множества нот.

Refridgerator
30.03.2022 06:20+1Тюнер — это не распознавание одной ноты. Тюнер — это точное вычисление частоты одной ноты, которая подаётся на вход в максимально чистом виде.
А в распознавании нот частотная точность вообще не важна, потому что частотные модуляции возникают как при игре на музыкальных инструментах, так и при различных интерференционных эффектах. А что действительно важно, так это:
1) последовательность нот;
2) отсутствие ложных срабатываний.
Причём на входе мы имеем полифонический сигнал с кучей шума, где одна мелодия на одном инструменте звучит поверх другой на другом инструменте поверх гармонической аккордовой последовательности на третьем. Вот, например, реальный спектр реального музыкального сигнала длиной 8192 отсчётов:спойлер
Какие ноты тут звучат, в какой последовательности, и сколько их? Интерполяция здесь вообще ничего не решает.
Makeman Автор
30.03.2022 07:50На всякий случай уточню, изначальная задача для приложения Solfeggio имеет наиболее общий характер: максимально точное распознавание частоты всех нот в аудиосигнале при коротких временных размерах окон (чтобы разобрать порядок звучания в реальном времени).
Например, если музыкант играет на клавишном инструменте, то программа должна показывать с достаточно высокой точностью, на какие клавиши он сейчас нажимает.
Для отдельно звучащих инструментов алгоритм справляется весьма неплохо. Помимо прочего программу можно использовать в качестве продвинутого музыкального тюнера, который позволяет производить настройку инструмента не только по одному обертону, но и сразу по нескольким.

Refridgerator
30.03.2022 06:35Большой вопрос к вычислительной сложности данного подхода...
Вычислительная сложность не имеет никакого значения, если вы не знаете, как именно это сделать. Здесь сложность прежде всего алгоритмическая, которая на несколько порядков выше, чем написать FFT.Transform(data).
Makeman Автор
30.03.2022 08:05Добавлен раздел «песочница» со ссылкой на онлайн-компилятор, где можно самому пощупать алгоритм и поиграть с входными данными сигнала.
Мне будет очень интересно познакомиться с альтернативными подходами, которые обеспечат примерно такой же качественный уровень распознавания при сопоставимой алгоритмической сложности...

Refridgerator
30.03.2022 08:20+1Где-то на хабре была статья об анализе с использованием гетеродина. Ну а дальше — google и sci-hub всё ещё пока доступны, ключевые слова «cepstrum», «filter bank», «continuous wavelet».

Makeman Автор
30.03.2022 09:21Не-не, имею в виду готовую реализацию на каком-либо языке программирования, чтоб можно было запустить и сравнить.
Так и сам могу кого угодно отослать по умным запросам, мол, изучайте, реализуйте и будет лучше, чем у вас. Поверьте, за годы исследований довелось познакомиться с немалым количеством материалов по теме обработки сигналов, но во многих случаях это теории или частные случаи. Так, чтобы рабочий код, это редкость.
Да, в открытом доступе есть реализации гитарных тюнеров на основе автокорреляции, но и они не лишены недостатков.
В статье представлен рабочий код, так что от «конкурентов» и альтернатив ожидается того же ;)

Refridgerator
30.03.2022 10:38+2Специализированные решения на основе этих «умных запросов» стоят дорого и очень дорого именно потому, что типичный школьник (имеется в виду уровень знания) их реализовать не в состоянии. Поэтому довольно странно ожидать, что ради спора в интернете кто-то будет тратить уйму сил и времени с выкладыванием результата в открытый доступ на радость конкурентам. В чём разница между FFT и вейвлетами я уже показывал — если и этого недостаточно, ну ок, чё.

Makeman Автор
30.03.2022 20:26Благодарю за ссылку. Для определённых задач вейвлеты очень даже годный инструмент, но вычислительно он на порядки дороже БПФ (из моих изысканий), что ограничивает их область применения, в особенности при обработке сигналов в реальном времени.
Не оспариваю тот факт, что различными подходами можно увеличивать точность распознавания гармоник, но опять же это требует дополнительных ресурсов.
Из моего опыта, связка БПФ и ФАИ - это в практическом смысле наиболее оптимальный путь достижения довольно высокой точности распознавания при минимальных затратах вычислительных ресурсов.
Возможно, если эту связку использовать для подготовительного анализа сигнала, а потом уже уточнять свойства гармоник другими методами, то можно будет достичь и ещё более впечатляющих результатов...
Но для моих задач точности хватало, поэтому такими экспериментами не занимался. Проект же развивается на энтузиазме, мне просто интересно разбираться в этой теме, поэтому делюсь результатами в открытом доступе :)






N-Cube
В статье сначала речь идет о классическом Фурье преобразовании бесконечного сигнала, но в реализации внезапно говорится про прямоугольное окно, то есть это уже другое преобразование (оконное). Это разные преобразования с различными свойствами и применимостью, а при неверном выборе окна можно совершенно фантастические эффекты получить. Очевидно, если размер окна меньше периода исследуемого сигнала, результат не имеет смысла. Кроме того, существуют такие известные проблемы, как явление (эффект) Гиббса, делающий невозможным восстановление исходного сигнала даже в теории, если только сигнал не удовлетворяет определенным ограничениям. В статье же не приведено никакой оценки самого сигнала и валидности выбранных параметров и результатов, так что и полученные результаты могут быть совершенно неверны и построенные на их основании выводы тоже. Если автор хотел показать практическое применение Фурье преобразования, то нужно это делать корректно, а не методом тыка, авось красивый график получится и все равно, имеет ли он хоть какой-то смысл.
Makeman Автор
Спасибо за интерес к материалам!
Цель этой статьи - поделиться мощным рабочим рабочим инструментом, который был выработан в результате многолетнего труда. Исследовать же его свойства на различных размерах окон и типах сигналов можно самостоятельно, скачав приложение Solfeggio (для Windows) или воспользовавшись исходными кодами.
Это не только красивые графики - это надёжный рабочий метод интерполяции, который по ряду показателей обходит другие подходы и алгоритмы для высокоточного анализа сигналов.