Содержание данной статьи изначально было опубликовано в последней книге автора статьи "Упрощение машинного обучения с PyCaret". Вы можете кликнуть здесь, чтобы ознакомиться с ней подробнее.

Одной из фундаментальных задач неконтролируемого машинного обучения является кластеризация. Цель этой задачи — классифицировать экземпляры заданного набора данных в различные кластеры на основе их общих характеристик. Кластеризация имеет множество практических применений в различных областях, включая маркетинговые исследования, анализ социальных сетей, биоинформатику, медицину и другие. В этой статье мы рассмотрим пример кластеризации с помощью PyCaret, библиотеки Python, которая поддерживает все основные задачи машинного обучения, такие как регрессия, классификация, кластеризация и обнаружение аномалий. PyCaret упрощает рабочий процесс машинного обучения, следуя лоукод-концепции, что делает ее отличным выбором как для новичков, так и для экспертов, которые хотят быстро создавать прототипы ML-моделей.

Требования к программному обеспечению

Код из статьи должен работать на всех основных операционных системах, т.е. Microsoft Windows, Linux и Apple macOS. На вашем компьютере необходимо инсталлировать Python 3, а также JupyterLab. Я предлагаю вам использовать Anaconda, набор инструментов для машинного обучения и даталогии, который включает в себя множество полезных библиотек и программных пакетов. Anaconda можно свободно загрузить по этой ссылке. В качестве альтернативы вы можете использовать облачный сервис, например, Google Colab, чтобы выполнять код на Python, не беспокоясь об установке чего-либо на вашем компьютере. Создайте новый блокнот Jupyter и введите код или загрузите его из этого репозитория Github.

Инсталляция PyCaret

Библиотеку PyCaret можно установить локально, выполнив следующую команду в терминале Anaconda. Эту же команду можно выполнить на Google Colab или аналогичном сервисе, чтобы установить библиотеку на удаленном сервере.

pip install pycaret[full]==2.3.4

После выполнения этой команды PyCaret будет инсталлирован, и вы сможете запустить все приведенные в статье примеры кода. Рекомендуется также установить дополнительные зависимости, включив спецификатор [full]. Кроме того, установка правильной версии пакета гарантирует максимальную совместимость, так как я использовал PyCaret ver. 2.3.4 во время работы над этой статьей. Наконец, создание среды conda для PyCaret считается лучшей практикой, так как это поможет вам избежать конфликтов с другими пакетами и убедиться, что у вас всегда инсталлированы правильные зависимости.

Кластеризация K-Means

Кластеризация K-Means¹ (К-средних) является одним из самых популярных и простых методов кластеризации, что делает его простым для понимания и реализации в коде. Он определяется следующей формулой.

K — это количество всех кластеров, а C представляет каждый отдельный кластер. Наша цель — минимизировать W, который является мерой внутрикластерной вариации.

Существуют различные способы определения внутрикластерной вариации, но наиболее распространенным является квадратичное евклидово расстояние, как видно из приведенного выше уравнения. В результате получается следующая форма кластеризации K-Means, где W заменяется формулой евклидова расстояния.

Кластеризация с помощью PyCaret

K-Means является наиболее распространенным методом, но существует множество других, таких как Affinity Propagation², Spectral Clustering³, Agglomerative Clustering⁴, Mean Shift Clustering⁵ и Density-Based Spatial Clustering (DBSCAN)⁶. Сейчас мы увидим, как модуль кластеризации PyCaret может помочь нам легко обучить модель и оценить ее эффективность.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from pycaret.clustering import *
from sklearn.datasets import make_blobs
mpl.rcParams['figure.dpi'] = 300

Начнем с импорта некоторых стандартных библиотек Python, включая NumPy, pandas, Matplotlib и Seaborn. Мы также импортируем функции кластеризации PyCaret, и функцию make_blobs() scikit-learn, которая может быть использована для создания датасетов. Наконец, устанавливаем DPI рисунка Matplotlib на 300, чтобы получить графики высокого разрешения. Включение этого параметра не обязательно, поэтому при желании вы можете удалить последнюю строку.

Генерация синтетического датасета

cols = ['column1', 'column2', 'column3',
        'column4', 'column5']
arr = make_blobs(n_samples = 1000, n_features = 5, random_state =20,
                 centers = 3, cluster_std = 1)
data = pd.DataFrame(data = arr[0], columns = cols)
data.head()

data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 5 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   column1  1000 non-null   float64
 1   column2  1000 non-null   float64
 2   column3  1000 non-null   float64
 3   column4  1000 non-null   float64
 4   column5  1000 non-null   float64
dtypes: float64(5)
memory usage: 39.2 KB

Вместо того чтобы загружать реальный датасет, мы будем генерировать синтетический, используя функцию make_blobs() scikit-learn. Эта функция генерирует датасеты, подходящие для моделей кластеризации, и имеет различные параметры, которые могут быть изменены в соответствии с нашими потребностями. В данном случае мы создали датасет с 1000 экземплярами, 5 признаками и 3 отдельными кластерами. Использование синтетического датасета для тестирования нашей модели кластеризации имеет различные преимущества, главным из которых является то, что мы уже знаем фактическое количество кластеров, и поэтому сможем легко оценить производительность модели. Реальные данные обычно сложнее, т.е. не всегда имеют четко разделенные кластеры, но работа с простым датасетом позволит лучше ознакомиться с инструментами и рабочим процессом.

Исследовательский анализ данных

data.hist(bins = 30, figsize = (12,10), grid = False)
plt.show()

Функция hist() pandas позволяет нам легко визуализировать дистрибьюцию каждой переменной. Мы видим, что все распределения переменных являются бимодальными или мультимодальными, т.е. имеют два или более пиков. Обычно это происходит, когда датасет содержит несколько групп с различными характеристиками. В данном случае датасет был специально создан для того, чтобы содержать 3 отдельных кластера, поэтому вполне разумно, что переменные имеют мультимодальное распределение.

plt.figure(figsize=(10, 8))
sns.heatmap(data.corr().round(decimals=2), annot=True)
plt.show()

Для создания тепловой карты, визуализирующей значения корреляции всех пар переменных, были использованы функция corr() pandas, а также функция heatmap() Seaborn. Мы видим, что столбец2 и столбец3 имеют сильную линейную зависимость со значением корреляции 0,93. То же самое верно для столбца3 и столбца4, значение корреляции которых составляет 0,75. С другой стороны, столбец1 имеет обратную корреляцию со всеми другими столбцами, но особенно со столбцом5, со значением -0,85.

plot_kws = {'scatter_kws': {'s': 2}, 'line_kws': {'color': 'red'}}
sns.pairplot(data, kind='reg', vars=data.columns[:-1], plot_kws=plot_kws)
plt.show()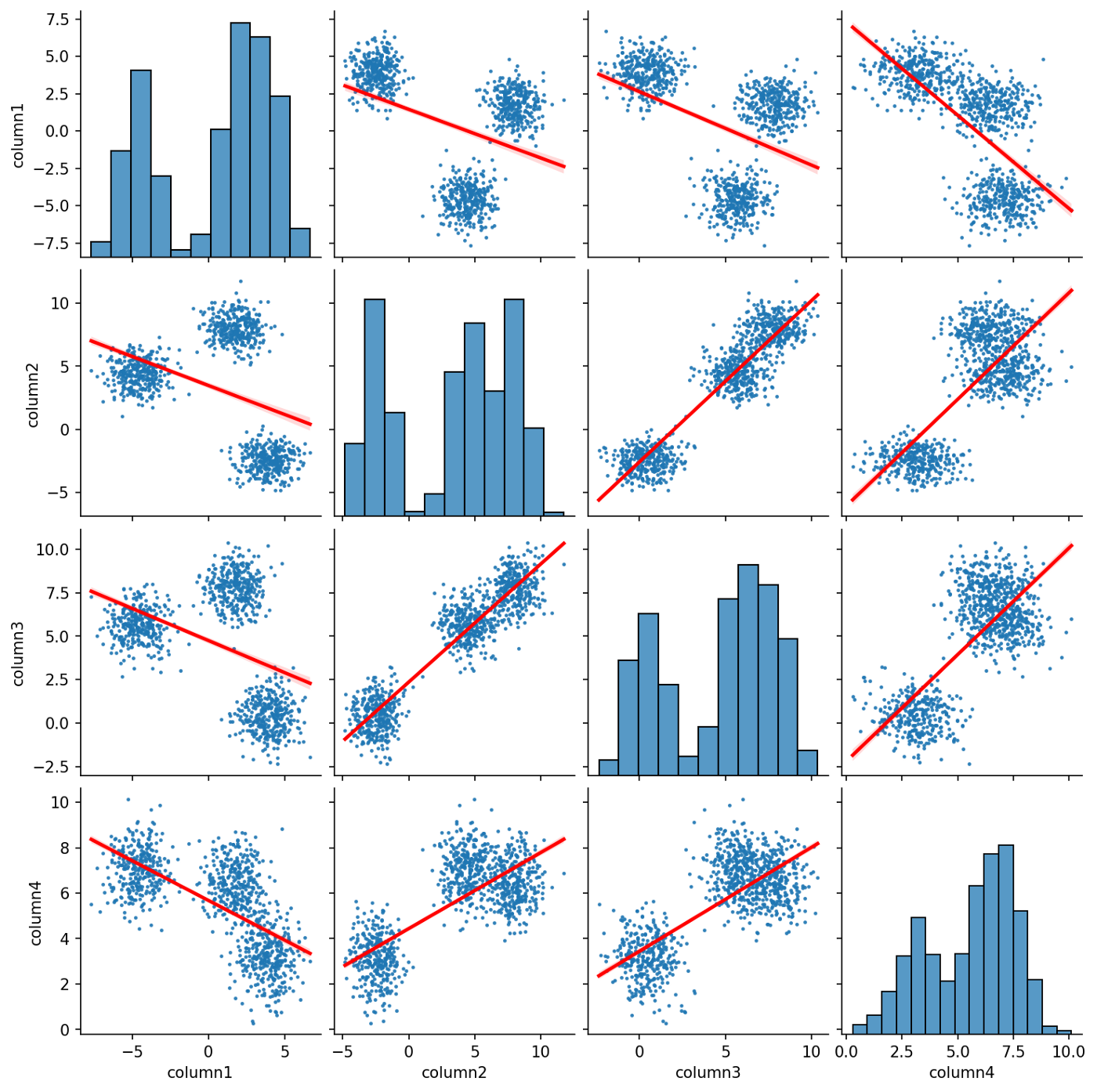

Мы использовали функцию pairplot() Seaborn для создания матрицы диаграмм разброса для синтетического датасета, диагональ которой представляет собой гистограмму каждой переменной. Кластеры датасета видны на диаграммах разброса, что указывает на то, что они четко отделены друг от друга. Как и ранее на тепловой карте корреляции, мы видим, что некоторые пары переменных имеют сильную линейную связь, а другие - обратную линейную связь. Это выделяется линиями регрессии, которые были включены в каждую диаграмму рассеяния путем установки параметра kind функции pairplot() на reg.

Инициализация среды PyCaret

cluster = setup(data, session_id = 7652)

После завершения исследовательского анализа данных (Exploratory Data Analysis. EDA) мы собираемся использовать функцию setup() для инициализации среды PyCaret. При этом будет создан пайплайн, который подготовит данные для обучения и развертывания модели. В данном случае настройки по умолчанию являются приемлемыми, поэтому мы не будем изменять ни один из параметров. Тем не менее, такая мощная функция обладает многочисленными возможностями по предварительной обработке данных, поэтому вы можете обратиться к странице документации модуля PyCaret Clustering, чтобы узнать об этом более подробно.

Создание модели

model = create_model('kmeans')

Функция create_model() позволяет нам легко создавать и оценивать предпочитаемую модель кластеризации, например, алгоритм K-Means. По умолчанию эта функция создает 4 кластера, поэтому достаточно установить параметр num_clusters равным 3, так как это является правильным числом. Вместо этого мы будем следовать подходу, характерному для реальных датасетов, где число кластеров, как правило, неизвестно. После выполнения функции выводится ряд показателей производительности, включая Silhouette⁷, Calinski-Harabasz⁸ и Davies-Bouldin⁹. Мы сосредоточимся на коэффициенте Silhouette, который определяется следующим уравнением.

• s(i) — коэффициент Silhouette для экземпляра i датасета.

• a(i) — среднее внутрикластерное расстояние i.

• b(i) — среднее расстояние до ближайшего кластера i.

Полученное значение метрики — это средний коэффициент Silhouette для всех экземпляров, имеющий диапазон от -1 до 1. Отрицательные значения указывают на то, что экземпляр был определен в неправильный кластер, а значения, близкие к 0, указывают на то, что кластеры перекрываются. С другой стороны, положительные значения, близкие к 1, указывают на правильное распределение. В нашем примере значение равно 0,5822, что говорит о том, что производительность модели может быть улучшена путем подбора оптимального количества кластеров для данного датасета. Далее мы рассмотрим, как этого можно добиться с помощью "метода локтя" (elbow method).

plot_model(model, 'elbow')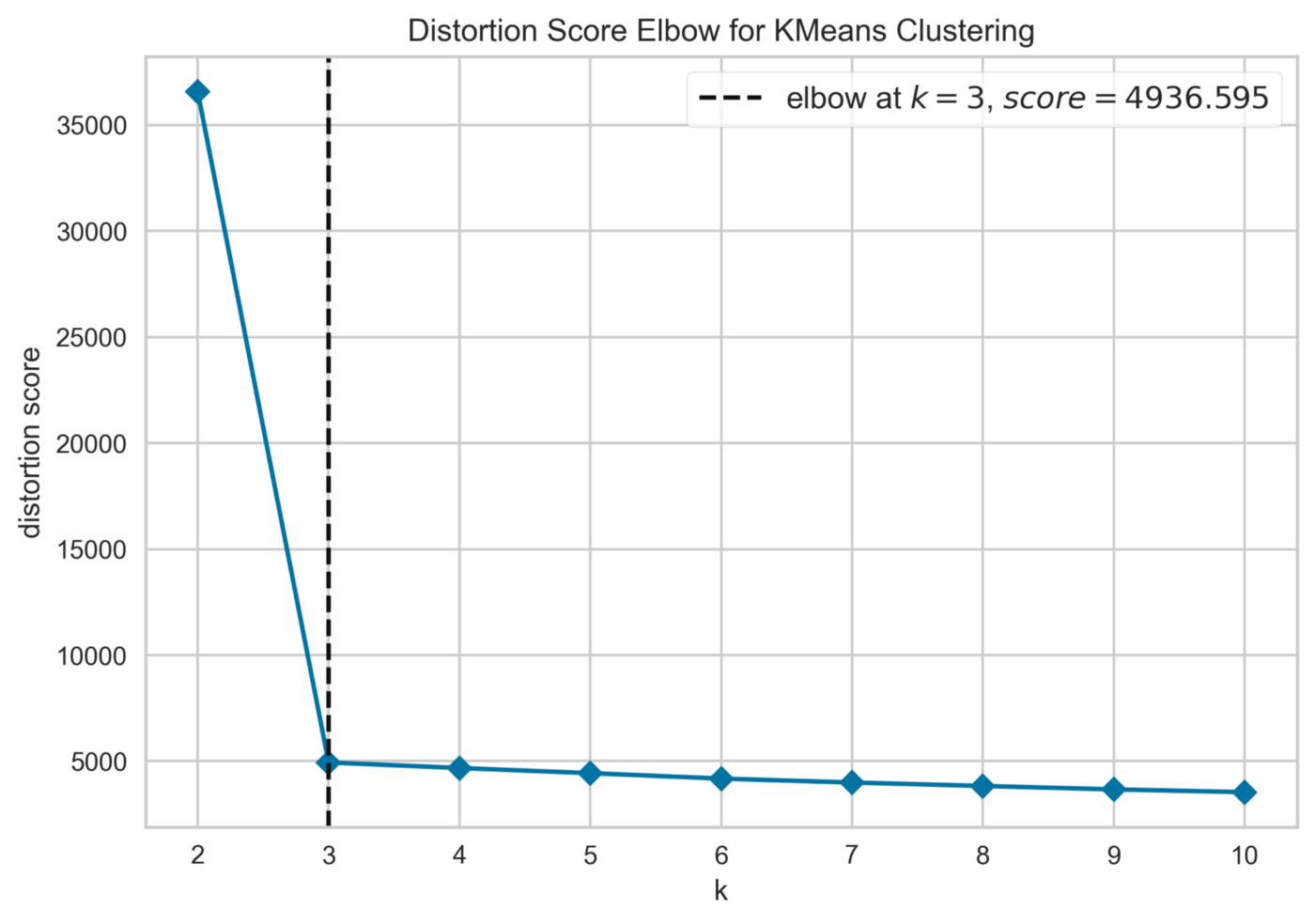

Функция plot_model() позволяет нам создавать различные полезные графики для нашей модели. В данном случае мы создали график локтя, который поможет нам найти оптимальное количество кластеров для модели K-Means. Метод локтя обучает модель кластеризации для ряда значений K и визуализирует оценку искажения для каждого из них¹⁰. Точка перегиба на кривой — известная как локоть — является показателем оптимального значения для K. Как и ожидалось, на графике есть локоть при K = 3, выделенный пунктирной вертикальной линией.

model = create_model('kmeans', num_clusters = 3)

После использования метода локтя для поиска оптимального количества кластеров мы снова проводим обучение модели K-Means. Как видно, средний коэффициент Silhouette увеличился до 0,7972, что указывает на улучшение работы модели и лучшее распределение кластеров для каждого экземпляра датасета.

Построение графика модели

plot_model(model, 'cluster')

Как было показано ранее, plot_model() — полезная функция, которую можно использовать при построении различных видов графиков для нашей модели кластеризации. В данном случае мы создали 2D график метода анализа главных компонент (Principal Component Analysis. PCA) для модели K-Means. PCA может использоваться для проецирования данных в пространство более низкой размерности с сохранением большей части дисперсии¹¹, эта техника известна как уменьшение размерности. После применения PCA к синтетическому датасету исходные 5 характеристик были редуцированы до 2 главных компонент. Кроме того, мы видим, что кластеры четко разделены, и все экземпляры датасета были назначены в правильный кластер.

Сохранение и назначение модели

save_model(model, 'clustering_model')
results = assign_model(model)
results.head(10)

Функция save_model() позволяет нам сохранить модель кластеризации на локальном диске для дальнейшего использования или развертывания в качестве приложения. Модель хранится в виде pickle-файла, который может быть загружен с помощью комплементарной функции load_model(). Кроме того, функция assign_model() возвращает синтетический датасет с дополнительным столбцом для кластерных меток, которые были присвоены экземплярам датасета.

Заключение

Надеюсь, что представленное в этой статье тематическое исследование поможет вам лучше освоить модуль кластеризации PyCaret. Я также призываю читателей экспериментировать с другими датасетами и самостоятельно практиковать вышеупомянутые техники. Если вы хотите узнать больше о PyCaret, то можете ознакомиться с книгой Simplifying Machine Learning with Pycaret, которую я недавно опубликовал. 

Сегодня в 20:00 состоится открытое занятие «Знакомство с Jupyter Notebook, основы Python». На нем познакомимся с Python и средой разработки Jupiter Notebook, а также узнаем, какие бывают типы данных и виды арифметических операций. Регистрация доступна по ссылке.