Речь пойдёт об алгоритме Витерби, коэффициенте однозначности, о смысловом их сходстве и различии.
Для Витерби должны быть даны или рассчитаны: вероятности скрытых начальных состояний, переходные вероятности и вероятности выбросов.
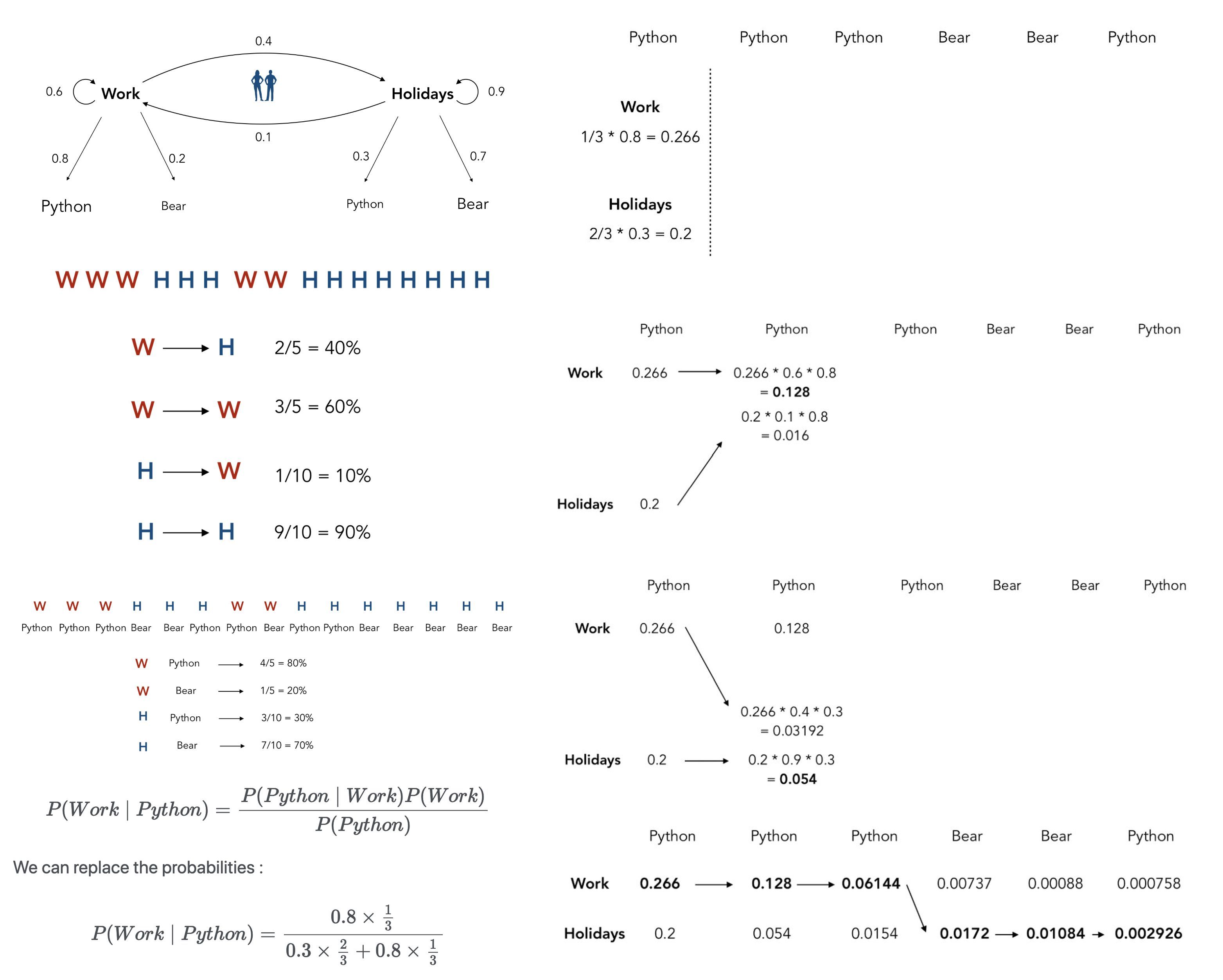
Его математическая суть:

где x- текущее скрытое состояние, y - следующее скрытое состояние, f - наблюдаемое состояние.
С учётом Байеса эту формулу можно преобразовать.

P(F): вероятность действия F (что соответствует состоянию в Витерби)
P(X|F): вероятность состояния Х (скрытое состояние в Витерби) при условии действия F
P(Y|X): вероятность следующего состояния Y (следующее скрытое в Витерби) при условии состояния X
В этой формуле, при допущении значений этих вероятностей близких единице, P(Y)=P(F)*P(X|F)*P(Y|X) однозначно выдаст следующее состояние Y. Идейно это тот же модус поненс. Зная F, можно получить Y.

Хотя алгоритм, рассчитывающий коэффициент однозначности, и алгоритм Витерби, решают внешне схожие задачи, назначение у них разное. С коэффициентом однозначности неважно предварительное знание вероятностей и неважно является ли последовательность (как действий, так и состояний) марковской. Что позволяет использовать его «на лету». Суть в том, что если известна последовательность действий, то в силу значения коэффициента равным единице или почти единице, последовательность состояний однозначно выводима.
Другими словами, если есть не детерминированный конечный автомат, то можно подобрать такие действия, что он становится детерминированным. Или почти детерминированным. С учётом ограничения на этот коэффициент как гиперпараметра.
#Пусть имеется три последовательности и нужно понять влияют ли они друг на друга
[1, 2, 1, 1, 2, 2, 1, 2, 2, 1]
[3, 4, 4, 3, 3, 4, 3, 3, 4, 3]
[5, 6, 5, 6, 5, 6, 5, 6, 5, 5]В этом случае можно составить несколько пар последовательностей. И по каждой паре проверить коэффициент однозначности. Видно по выводу ниже, что [3, 4, 4, 3, 3, 4, 3, 3, 4, 3] являются действиями для состояний [1, 2, 1, 1, 2, 2, 1, 2, 2, 1]. Однозначность для этой пары 100%. Как следствие - возможность прокладывать маршруты в таком графе.
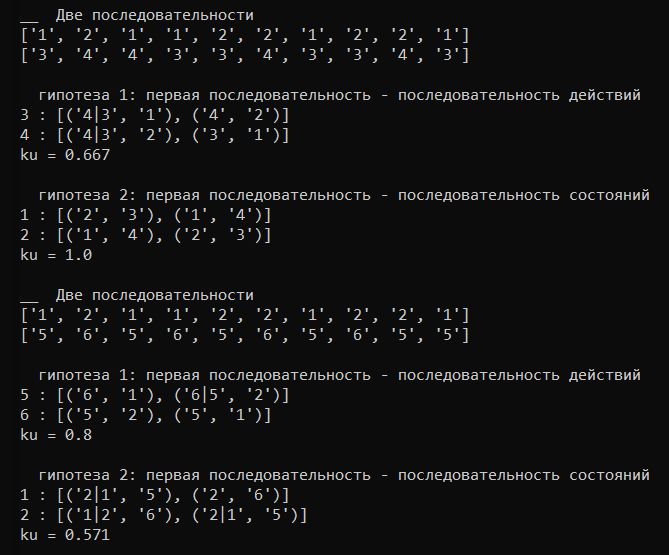
Для сравнения проанализируем алгоритмом Витерби. Если взять те же последовательности, то налицо ошибки 2/6.
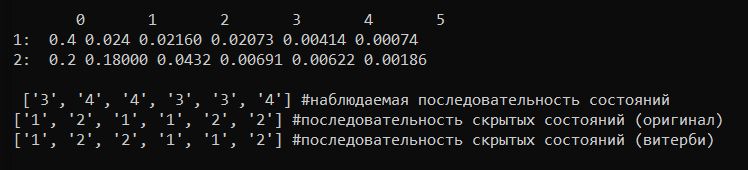
С другой стороны, если рассмотреть последовательности как здесь, то результат будет обратным. Коэффициент однозначности низкий. Витерби дает большую предсказуемость.
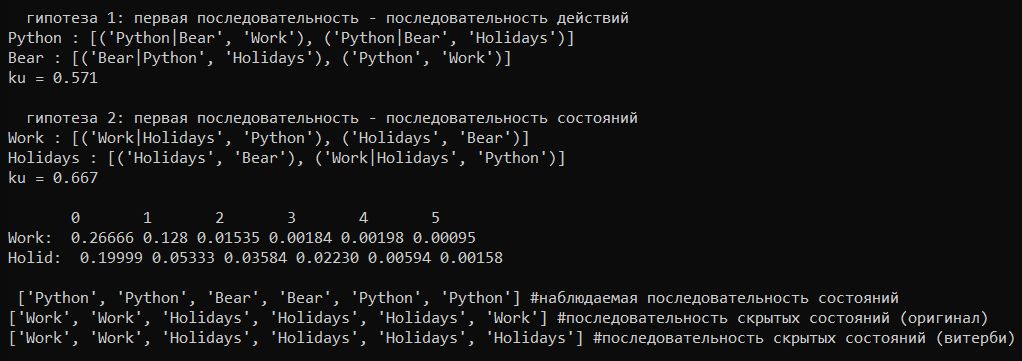
Для Витерби важно условие, чтобы последовательность являлась марковской.

Проверяем последовательность из книги Эшби и из статьи. Ни та, ни другая ею не являются. После (Holidays, Work) Holidays даже не следует. По крайней мере для той ее длины.

Итак, для алгоритма Витерби нужно предварительное длинное наблюдение, чтобы иметь вероятности, рассчитанные в результате этих наблюдений Также он ограничен марковским свойством. Алгоритм с расчетом на коэффициент однозначности лишен этих недостатков, но и предназначение у него иное: он нацелен на выявление детерминированных или почти детерминированных явлений.
import random
import matplotlib.pyplot as plt
class Hd():
def __init__(self, graph):
self.graph = graph
def rnd_get(self, v):
return random.choice(v.split("|"))
def show(self, graph):
for x in graph:
print(x, ":", graph[x])
def get_ku(self, graph):
'''return (коэффициент однозначности, размер)'''
n = 0; u = 0
for x in graph:
for y in graph[x]:
if y[0]:
u += y[0].count("|")
n += 1
if n != 0:
return (round(1- u/(n+u), 3), n)
else:
return (None, None)
def get_states(self, x, f_list = [], n=11):
''' На входе последовательность действий и начальное состояние
На выходе последоваельность состояний'''
x_list = []
x_list.append(x)
if f_list != []:
for f in f_list:
xf = [xf for xf in g[x] if xf[1] == f]
if not xf:
x_list.append(''); f_list[len(x_list)-2] = ''
return (x_list, f_list[:len(x_list)-1])
x = self.rnd_get(xf[0][0])
x_list.append(x)
else:
for i in range(n):
if not self.graph[x]:
x_list.append(''); f_list.append('')
break
t = random.choice(self.graph[x])
f = t[1]
x = random.choice(t[0].split('|'))
x_list.append(x); f_list.append(f)
if len(f_list) == len(x_list) -1:
return (x_list, f_list)
else:
return ([], [])
def get_yfx(self, f_list, x_list, t = True):
'''возвращаем список кортежей (x, f, y)'''
if len(x_list) == len(f_list):
x_list.append('')
path = []
for i in range(len(f_list)):
path.append((x_list[i], f_list[i], x_list[i+1]))
if t:
return path
else:
p = []
for xfy in path:
if xfy[2] != '':
p.append(xfy[2]+'='+xfy[1]+'('+xfy[0]+')')
return p
def flow(self, path, rnd=False):
if not path: return []
fl = []
for p in path:
if not rnd:
fl.append(p[:-1])
else:
pr = list(p[:-1])
random.shuffle(pr)
fl.append(tuple(pr))
return fl
def fORx(self, flow, f=0):
'''на входе поток, на выходе две гипотезы
index: f=0, x=1 or x=0, f=1'''
def add_empty():
empty = []
for k in graph:
for x in graph[k]:
z = list(set(x[0].split('|')) - set(list(graph.keys())))
if z:
empty.append(z[0])
return empty
if not flow: return []
graph = {}
fli = flow[0]
for t in flow[1:]:
if f == 0:
if fli[1] not in graph:
graph[fli[1]] = []
r = [(i, xf) for i,xf in enumerate(graph[fli[1]]) if xf[1] == fli[0]]
if r:
if t[1] not in r[0][1][0]:
x_new = r[0][1][0] + "|" + t[1]
if x_new != '':
graph[fli[1]][r[0][0]] = (x_new, r[0][1][1])
if not r:
if t[1] != '':
graph[fli[1]].append((t[1], fli[0]))
if f == 1:
if fli[0] not in graph:
graph[fli[0]] = []
r = [(i, xf) for i,xf in enumerate(graph[fli[0]]) if xf[1] == fli[1]]
if r:
if t[0] not in r[0][1][0]:
x_new = r[0][1][0] + "|" + t[0]
if x_new != '':
graph[fli[0]][r[0][0]] = (x_new, r[0][1][1])
if not r:
if t[0] != '':
graph[fli[0]].append((t[0], fli[1]))
fli = t
em = add_empty()
if em:
graph[em[0]] = []
return graph
def merge(self, g1, g2):
'''объединяет два графа в один'''
def find_index():
for i in range(len(graph[k])):
if graph[k][i][1] == x[1]:
return i
return -1
all_keys = set(list(g1.keys()) + list(g2.keys()))
graph = {}
for k in all_keys:
if k not in graph:
if k in g1:
graph[k] = g1[k]
else:
graph[k] = g2[k]
if k in g2:
for x in g2[k]:
ind = find_index()
if ind != -1:
if x[0] != []:
t1 = x[0].split('|')
if graph[k][ind] != -1:
t2 = graph[k][ind][0].split('|')
z = "|".join(set(t1+t2))
xf = [z, graph[k][ind][1]]
graph[k][ind] = xf
else:
graph[k].append(x)
return graph
class Vm():
def print_dptable(self, V):
'''https://russianblogs.com/article/255172857/'''
for i in range(len(V)): print("%8d" % i, end="")
print()
for y in V[0].keys():
print("%.5s: " % y, end=" ")
for t in range(len(V)):
print("%.7s" % V[t][y], end=" ")
print()
def viterbi(self, obs, states, start_p, trans_p, emit_p):
'''https://russianblogs.com/article/255172857/'''
V = [{}]
path = {}
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
path[y] = [y]
for t in range(1, len(obs)):
V.append({})
newpath = {}
for y in states:
(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
V[t][y] = prob
newpath[y] = path[state] + [y]
path = newpath
self.print_dptable(V)
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return prob, path[state]
def startProbability(self, x_list):
'''расчет начальной вероятности'''
start_probability = {}
for z in x_list:
if z not in start_probability:
start_probability[z] = 1
else:
start_probability[z] +=1
start_probability = {z:start_probability[z]/(len(x_list)) for z in start_probability}
return start_probability
def transitionProbability(self, x_list):
'''расчет переходной вероятности'''
transition_probability = {}
for i,z in enumerate(x_list):
if z not in transition_probability:
transition_probability[z] = {}
if i == 0:
z_old = z
continue
if z not in transition_probability[z_old]:
transition_probability[z_old][z] = 1
else:
transition_probability[z_old][z] = transition_probability[z_old][z] +1
z_old = z
for z_old in transition_probability:
z_list = [transition_probability[z_old][z] for z in transition_probability[z_old]]
for z in transition_probability[z_old]:
transition_probability[z_old][z] = transition_probability[z_old][z] / sum(z_list)
return transition_probability
def emissionProbability(self, x_list, f_list):
'''расчет вероятности выброса'''
emission_probability = {}
for i,z in enumerate(x_list):
if z not in emission_probability:
emission_probability[z] = {}
if f_list[i] not in emission_probability[z]:
emission_probability[z][f_list[i]] = 1
else:
emission_probability[z][f_list[i]] += 1
for z_old in emission_probability:
z_list = [emission_probability[z_old][z] for z in emission_probability[z_old]]
for z in emission_probability[z_old]:
emission_probability[z_old][z] = emission_probability[z_old][z] / sum(z_list)
return emission_probability
def isMarkov(self, w_list, prev_s, s):
'''проверка на марковское свойство'''
transition_probability = {}
for i,z in enumerate(w_list):
if z not in transition_probability:
transition_probability[z] = {}
if i == 0:
z_old = z
continue
if z not in transition_probability[z_old]:
transition_probability[z_old][z] = 1
else:
transition_probability[z_old][z] = transition_probability[z_old][z] +1
z_old = z
zz_old = z_old
transition_probability_ = {}
for i,z in enumerate(w_list):
if z not in transition_probability_ and z == s:
transition_probability_[z] = {}
if i == 0:
z_old = z
continue
if i == 1:
zz_old = z_old
z_old = z
continue
if zz_old == prev_s and z_old == s:
if z not in transition_probability_[z_old]:
transition_probability_[z_old][z] = 1
else:
transition_probability_[z_old][z] = transition_probability_[z_old][z] +1
zz_old = z_old
z_old = z
return ((prev_s, s), transition_probability_[s], transition_probability[s])
#--------- main ---------#
if __name__ == "__main__":
g = {}
hd = Hd(g)
print("\n__ Две последовательности")
x_list = [str(x) for x in [1, 2, 1, 1, 2, 2, 1, 2, 2, 1]]
f_list = [str(f) for f in [3, 4, 4, 3, 3, 4, 3, 3, 4, 3]]
print(x_list)
print(f_list)
path = hd.get_yfx(f_list, x_list)
print("\n гипотеза 1: первая последовательность - последовательность действий")
gn = hd.fORx(hd.flow(path), f=0)
hd.show(gn)
ku = hd.get_ku(gn)
print("ku =", ku[0])
print("\n гипотеза 2: первая последовательность - последовательность состояний")
gn = hd.fORx(hd.flow(path), f=1)
hd.show(gn)
ku = hd.get_ku(gn)
print("ku =", ku[0])
###########################
print("\n__ Две последовательности")
x_list = [str(x) for x in [1, 2, 1, 1, 2, 2, 1, 2, 2, 1]]
f_list = [str(f) for f in [5, 6, 5, 6, 5, 6, 5, 6, 5, 5]]
'''
x = "Work Work Work Holidays Holidays Holidays Work Work Holidays Holidays Holidays Holidays Holidays Holidays Holidays"
f = "Python Python Python Bear Bear Python Python Bear Python Python Bear Bear Bear Bear Bear"
x_list = x.split()
f_list = f.split()
'''
print(" гипотеза 1: первая последовательность - последовательность действий")
path = hd.get_yfx(f_list, x_list)
gn = hd.fORx(hd.flow(path), f=0)
hd.show(gn)
ku = hd.get_ku(gn)
print("ku =", ku[0])
print("\n гипотеза 2: первая последовательность - последовательность состояний")
gn = hd.fORx(hd.flow(path), f=1)
hd.show(gn)
ku = hd.get_ku(gn)
print("ku =", ku[0])
print("\n__Витерби")
x_list = [str(x) for x in [1, 2, 1, 1, 2, 2, 1, 2, 2, 1]]
f_list = [str(f) for f in [3, 4, 4, 3, 3, 4, 3, 3, 4, 3]]
'''
x = "Work Work Work Holidays Holidays Holidays Work Work Holidays Holidays Holidays Holidays Holidays Holidays Holidays"
f = "Python Python Python Bear Bear Python Python Bear Python Python Bear Bear Bear Bear Bear"
x_list = x.split()
f_list = f.split()
'''
states_x = set(x_list)
states_f = set(f_list)
observations = f_list[1:7]
states = states_x
vm = Vm()
start_probability = vm.startProbability(x_list)
transition_probability = vm.transitionProbability(x_list)
emission_probability = vm.emissionProbability(x_list, f_list)
r = vm.viterbi(observations,
states,
start_probability,
transition_probability,
emission_probability)
print("\n", observations, "#наблюдаемая последовательность состояний")
print(x_list[1:7], "#последовательность скрытых состояний (оригинал)")
print(r[1], "#последовательность скрытых состояний (витерби)")
print("\n__isMarkov")
w = 'A A B B A B B A A B B A B B A B B A B B A A B B A B B A B A B A'
w_list = w.split()
r = vm.isMarkov(w_list, 'A', 'B')
print(*r)
r = vm.isMarkov(w_list, 'B', 'B')
print(*r, "\n")
w = "Work Work Work Holidays Holidays Holidays Work Work Holidays Holidays Holidays Holidays Holidays Holidays Holidays"
w_list = w.split()
r = vm.isMarkov(w_list, 'Holidays', 'Work')
print(*r)
r = vm.isMarkov(w_list, 'Work', 'Work')
print(*r, "\n")
P.S. Для последовательностей [1, 2, 1, 1, 2, 2, 1, 2, 2, 1], [3, 4, 4, 3, 3, 4, 3, 3, 4, 3] им соответствующие графы будут выглядеть так, где пунктирной линией неоднозначность выделена. Коэффициент однозначности для первой гипотезы 0,67, т.к всего переходов 2+1+2+1, а если бы были только однозначны, то 4.
4|3 = 1(3) # из состояния 3 при действии 1 следует либо 4, либо 3
4 = 2(3) # из состояния 3 при действии 2 следует только 4.
4|3 = 2(4)
3 = 1(4)

Комментарии (9)

sunnybear
24.07.2022 09:14+1Почти единица на длинных последовательностях будет играть злую шутку. Здесь лучше более четкое определение через ограничение возможной ошибки.

bvv2311 Автор
24.07.2022 09:42+1Будет. Но что ж. Порой остается смириться... Сам КМС по шахматам. Аналогия такая. В какое-то время некоторые фигуры начинают ходить не так, как от них ожидалось. Неоднозначно. Слон как конь или вообще как-то иначе.


VPryadchenko
А можно начать с постановки задачи, для тех, кто не в теме? А то ничего непонятно, но очень интересно.
bvv2311 Автор
Алгоритм Витерби - поиск наиболее подходящего списка состояний (последовательности). Алгоритм с расчётом на коэффициент однозначности тоже на это нацелен. Разница в исходных требованиях. Для Ветирби необходимы вероятности и соблюдение марковского свойства. Но зато он может давать прогнозы на любые последовательности....
VPryadchenko
Ну это тоже не совсем постанова задачи, плюс я не про комментарии всё-таки - при желании любой может заглянуть в интернеты и найти нужную информацию. Я о том, что статью неплохо бы с постановки задачи начинать. Всегда )
VPryadchenko
Вот тут, например, Вы хорошо, на мой взгляд начали: https://habr.com/ru/post/656999/
Lelant0s
Присоединюсь к просьбе - можно какой-то пример практический привести? Для понимания потенциального диапазона задействованности этого алгоритма.