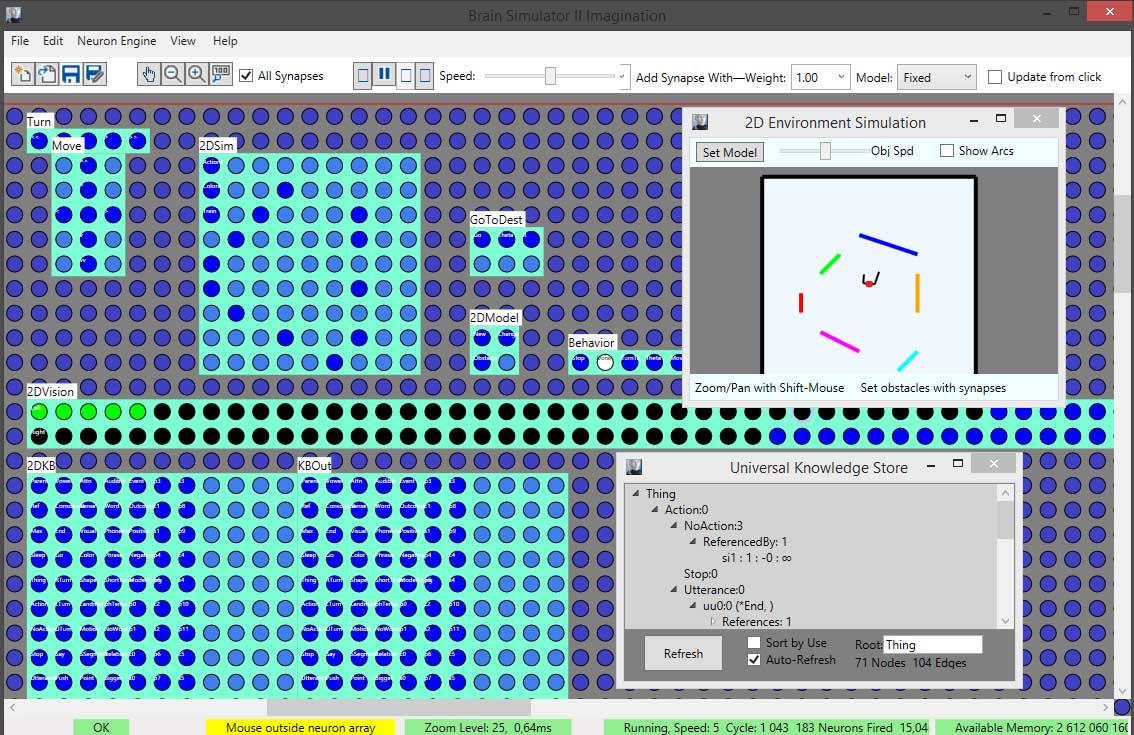
Здравствуйте, предлагаю обзор и разбор проекта Brain Simulator II от Чарльза Дж. Саймона, основателя FutureAI. Этот проект и компания малоизвестны, в русскоязычном сегменте интернета вообще нет никаких упоминаний о ней. Моё внимание компания привлекла благодаря сообщению о том, что недавно FutureAI привлекла 2 миллиона $ инвестиций. Проект оказался для меня очень любопытным и интересным, так как я сам во многом разделяю взгляды на проблематику создания AGI Чарльза Саймона, и у меня была практика создания симулятора подобного Brain Simulator II. Обзор проводится на основе общедоступных материалов с сайта FutureAI.guru, откуда можно свободно скачать сам симулятор (windows), а также найти ссылку на его исходный код (c#). Ниже будет представлен вольный перевод одной из статей с сайта, в сопровождении моих комментариев.

Чарльз Дж. Саймон признанный на национальном уровне предприниматель, разработчик программного обеспечения и менеджер. Обладает широким управленческим и техническим опытом, а также научными степенями в области электротехники и компьютерных наук, имеет многолетний опыт работы в IT, включая уникальный опыт работы в области искусственного интеллекта и САПР. Родом из Сан-Франциско, Калифорния, г-н Саймон стал соучредителем трех новаторских технологических компаний, где участвовал в качестве президента и вице-президента по инженерным вопросам. Его технический опыт включает создание двух уникальных систем искусственного интеллекта, а также программного обеспечения для оборудования по проведению неврологических тестов. Сочетание разработки искусственного интеллекта с биомедицинским тестированием нервных сигналов дает ему уникальные видение принципов работы мозга.

Использование отдельных нейронных спайков для репрезентации информации

Чарльз Дж. Саймон (источник).

Большая часть нервного возбуждения в коре мозга представляет собой случайные отдельные спайки, в среднем один раз в несколько секунд. Возникает вопрос: как может система из кажущихся случайных отдельных спайков представлять полезную информацию и приводить к общему интеллекту, демонстрируемому человеческим мозгом? Почти все искусственные нейронные сети представляют информацию в виде частоты срабатывания нейронов и хранят память в весовых коэффициентах синапсов. Кодирование частоты импульсов наблюдается в сенсорных и моторных нейронах, но анализ энергии показывает, что для подобного кодирования для большинства нейронов коры потребовалось бы значительно больше энергии. Также, веса синапсов хороши для кодирования долговременной памяти, но если учитывать время необходимое для перестройки синапса, то оно слишком велико, чтобы объяснить кратковременную память. В этой статье представлены смоделированные нейронные механизмы, которые могут преобразовывать сигналы основанные на частоте в сигналы представляющие собой отдельные спайки, и наоборот отдельные спайки в сигналы основанные на частоте. Затем обсуждается несколько механизмов кратковременной памяти и представления знаний в форме одиночных спайков. Это цифровая модель представляет собой другой подход к решению основных проблем ИИ. В совокупности эти алгоритмы представляют собой возврат к истинным нейроморфным методам как подходу продвижения к сильному искусственному интеллекту (AGI). Наконец, эти алгоритмы и методы существенно влияют на оценку количества информации, которую может обрабатывать человеческий мозг, и, как следствие, снижают требуемые вычислительной мощности, необходимой для создания AGI.

Современное программное обеспечение искусственного интеллекта, основанное на нейронах, основано на концепции, согласно которой частота возбуждения нейронов является представлением передаваемой информации. Энергетический анализ мозга показывает, что менее 1% нейронов в неокортексе активируются достаточно часто, чтобы представлять такие сигналы. Соответственно, мозг должен представлять информацию в виде, казалось бы, случайных отдельных спайков и коротких серий импульсов. В этой статье описываются методы преобразования частотных сигналов в одиночные параллельные сигналы с одним спайком и предлагаются нейронные схемы для обработки информации, а также ответы на некоторые базовые вопросы ИИ.

Эти методы представляют собой новое направление в исследований ИИ, отличное от ИНС/(обратного распространения ошибки), но более общее и нейроподобное, чем символьные подходы ИИ. Совместно, эти методы могут создать любую желаемую функциональность и объединить информацию от нескольких органов чувств, чтобы имитировать функциональность, базовую для интеллекта. Кроме того, эффективность этих подходов может сделать возможным сильный искусственный интеллект (AGI) на современном оборудовании, что окажет глубокое влияние на общество.

Все примеры в этом тексте, а также симулятор, использованный для их создания, находятся в свободном доступе для скачивания и проверки.

Паттерны нейронных спайков можно условно разделить на частотные, серийные и отдельные спайки. Сигналы, основанные на частоте, определенно присутствуют в зрительных и других сенсорных нейронах, а также в двигательных нервах. В то время как большинство нейронных моделей искусственного интеллекта сосредоточены исключительно на кодировании информации в частоте возбуждения нейронов, энергетический анализ неокортекса показывает, что этот тип передачи сигналов находится в меньшинстве. 

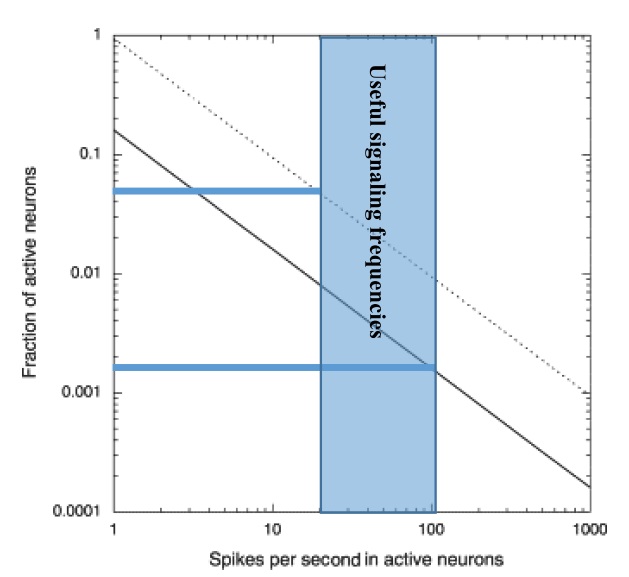
Значения в нижеследующих расчетах подвержены большим количеством экспериментальных данных. Расчет выполняется со значениями «наилучшей оценки», как показано на рисунке, за которыми следует диапазон ожидаемых результатов.

16 миллиардов нейронов неокортекса срабатывают с наилучшей оценкой в среднем 0,16 Гц (один раз каждые шесть секунд), генерируя 2,56x10⁹ нейронных импульсов в секунду [K. Grace, ed, “Neuron firing rates in humans”]. Это число основано на измеренном общем потреблении энергии неокортексом, деленным на расчетную энергию, затрачиваемую отдельными нейронами и синапсами при возбуждении. Эта низкая средняя частота возбуждения часто упускается из виду, потому что экспериментатор, исследующий нейроны, обычно интересуется нейронами, которые возбуждаются, и склонен игнорировать нейроны, которые не возбуждаются в интересующий период времени.

N_Rate, N_Burst и N_Single представляют количество нейронов зависящие от частоты, серии (череда импульсов) и одиночных спайков соответственно.

N_Rate + N_Burst + N_Single = 16х10⁹ нейронов

R * N_Rate + B * N_Burst + N_Single = 2.56х10⁹ спайков/с

Где R — средняя частота импульсов для сигналов с частотным представлением при использовании частоты 20 Гц (см. «Максимальная и минимальная частоты импульсов» на рисунке выше). B — количество импульсов в пакете, при этом используется 10.

С двумя уравнениями и тремя неизвестными конкретного решения нет, но поскольку количество нейронов не может быть отрицательным, максимальное значение N_Rate равно 128x10⁶ (оставляя 0 для двух других категорий). Если мы уменьшим N_Rate до 127x10⁶, то у нас останется 16x109 нейронов, которые представляют собой пакетные или одиночные нейроны, поскольку 127x10⁶ меньше, чем предел погрешности. При расчете в этом примере у нас осталось около 1,4x10⁹ нейронов, активирующихся сериями импульсов, и 14x10⁹ отдельными импульсами.

127x10⁶ представляет собой поразительно малую долю 0,8% нейронов неокортекса, кодирующих информацию частотами срабатывания. Остальные нейроны будут возбуждаться со средней частотой один импульс каждые 266 секунд — слишком медленно для большинства наблюдений.

На рисунке выше показан разумный диапазон возможных долей возбуждения нейронов в полезном частотном диапазоне от 5% до 0,2%.

Поскольку в подавляющем большинстве мы можем наблюдать нервные импульсы в виде коротких серий или одиночных импульсов, то большая часть вычислений в мозге, основанных на частоте, сосредоточена на входах сенсорных сигналах и создании моторных сигналов, которые, как известно, также основаны на частоте.

Максимальная и минимальная частота срабатывания нейронов

Биологические нейроны могут срабатывать с максимальной частотой около 200 Гц. После срабатывания наступает рефрактерный период, в течение которого никакая стимуляция не заставит нейрон снова возбудиться, что и устанавливает максимальную частоту активаций. Сигнал, изменяющийся во времени, будет иметь максимальную среднюю частоту 100 Гц. В течение рефрактерного периода ионы, используемые возбужденным нейроном, транспортируются обратно, поэтому процесс может повторяться бесконечно. Этот ионный транспорт требует незначительного количества энергии, но, помноженный на миллиарды нейронов в мозге, составляет ~12 Вт энергии, потребляемой мозгом. 

Минимальная частота срабатывания ограничена базовым представлением того, как часто или как быстро последовательность спайков должна представлять минимальный уровень сигнала. Рассмотрим представление тонов, участвующих в восприятии речи, где, как известно, присутствует кодирование сигналов на основе частоты. Люди могут говорить (и понимать речь) со скоростью более десяти слогов в секунду. Исходя из этого, мы можем предположить, что все поступающие слуховые сигналы должны передавать значение менее чем за 0,1 с. Это устанавливает минимальную полезную частоту срабатывания на уровне 10 Гц с минимальной средней частотой срабатывания 20 Гц.

Модель нейронов

Оставшаяся часть этой статьи демонстрирует, как нейроны потенциально могут представлять важную информацию в одиночных спайках. Нет никаких ожиданий, что все эти методы существуют в биологическом мозге, но некоторые из них вероятны. Нейронное моделирование, используемое для разработки схем в следующих примерах, было создано с помощью Brain Simulator II.

Разбирая идею отдельных спайков репрезентирующих информацию, необходимо использовать модели, основанные на спайках. Моделирование проводилось с помощью моделей нейронов IF (Integrate-and-Fire, “накапливай и активируйся”) и LIF (Leaky Integrate and Fire, “накапливай и активируйся с утечкой”). В обеих моделях нейроны накапливают воздействие от входящих нервных импульсов до тех пор, пока не будет достигнут порог, а затем испускают один импульс. Но в модели LIF накопленное воздействие уменьшается по экспоненциальному закону. Когда нейрон активируется, выходные синапсы, соединяющие его с другими нейронами, вносят вклад в суммирующие воздействие этих нейронов на величину веса синапса.

Обе модели более правдоподобны с биологической точки зрения, чем модели с ИНС постоянного действия. Доступны более биологически точные модели, но в данном обсуждении используются модели IF и LIF, более биологически точные модели выходят за рамки представленных здесь схем, поэтому они не будут полезными. Кроме того, используемые здесь модели отличаются от биологических в двух важных аспектах: 1) время является дискретным, а не непрерывным, и 2) все спайки достигают нейронов-мишеней одновременно. Эти различия не умаляют полезности моделей.

В общем, спаковые модели более эффективны с вычислительной точки зрения, чем общие модели ИНС, поскольку вычисления требуются только тогда, когда нейрон срабатывает. Поскольку мы рассматриваем нервный импульс как редкое событие, вычислительная эффективность возрастает еще больше.

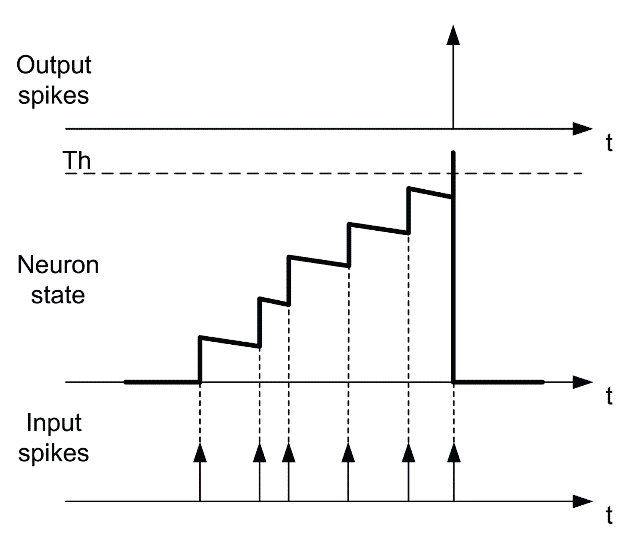
Следующие уравнения определяют функцию модели LIF, реализованную в моделировании.

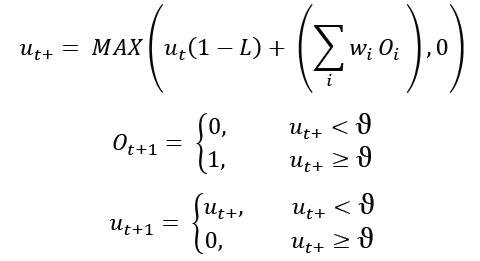
Где u_t — потенциал мембраны нейрона в момент времени t.  u_t+ — промежуточное значение. L – скорость утечки, диапазон от 0 до 1. ????_???? — это входящие синаптические сигналы от других нейронов, равные 1 или 0. ????_????, синаптический вес, может иметь любое значение, но обычно находится в диапазоне от -1 до 1. Порог ϑ имеет определенное значение 1, при этом все остальные значения масштабируются соответствующим образом. 

Обратите внимание, что если скорость утечки равна 0, то модель LIF становится моделью IF, и внутренние значения будут навсегда сохранятся. При скорости утечки, равной 1, нейрон будет реагировать на свой текущий вход без какого-либо внутреннего накопления заряда. Хотя эти значения не являются биологически правдоподобными, они могут быть полезны и означать, что вся модельная функция может выполняться без каких-либо умножений, только (более быстрые) сложения. В используемой здесь модели LIF экспоненциальное затухание аппроксимируется дискретным сокращением в течение каждого нейронного цикла.

Синапсы

В моделировании веса синапсов представлены числами с плавающей запятой, в то время как биологические синапсы, по-видимому, ограничены примерно 100 дискретными значениями [J.M.. Montgomery, D.V. Madison. “Discrete synaptic states define a major mechanism of synapse plasticity”]. В то время как большинство биологических нейронов имеют веса, которые обычно довольно малы (в диапазоне 0,01 или меньше в этом масштабе), синапсы с более высоким весом могут быть достигнуты с помощью нескольких параллельных синапсов.

В последующих обсуждениях синапсы имеют фиксированные веса. Начиная с раздела «Нейронный граф», существует потребность в синапсе с переменным весом, вес которого может меняться для представления информации. Этот «Синапс Хебба» будет описан в соответствующем разделе.

Логические элементы на нейронах

Можно утверждать, что эта модель нейрона представляет собой функционально законченный набор, а это означает, что любая цифровая схема может быть создана из нейронов LIF. Можно определить логический 0 как нейрон, который вообще не активируется, а логическую 1 — как нейрон, активирующийся с максимальной частотой. Хотя это легко понять, недостатком такого определения является то, что 0 требует мало энергии, в то время как 1 использует энергию с чрезмерной степенью. Это контрастирует с электронной логической схемой, которая рассеивает энергию и имеют небольшую разницу между логическим 0 и 1. Как следствие, этот тип логической схемы не получил бы широкого распространения в мозгу.

Частотное преобразование импульсных сигналов

В большинстве сенсорных систем частота возбуждения увеличивается, как правило, нелинейно, с увеличением интенсивности стимула. В качестве примера  частотно-кодированного сигнала мы можем наблюдать в зрительном нерве, что некоторые нейронные сигналы имеют частоту срабатывания, которая зависит от интенсивности света, воспринимаемого в определенном месте сетчатки. Чтобы быть полезным, такой сигнал должен иметь значение 0,05с или быстрее, чтобы соответствовать нашей наблюдаемой способности быстро распознавать объекты.

Если у нейрона есть один вход с весом синапса 0,9, то он не сработает на одном импульсе. Очевидно, что при соответствующем выборе скорости утечки нейрон LIF может срабатывать с любой входящей частотой. То есть, если скорость входящих сигналов превышает скорость утечки, заряд нейрона увеличится и сработает. Если скорость утечки превышает скорость входящего сигнала, нейрон никогда не сработает. Скорость утечки должна быть установлена по формуле:

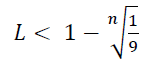
Где L — скорость утечки, а n — количество временных циклов между импульсами. К примеру, начальный импульс дает нейрону заряд 0,9. Если следующий импульс произойдет до того, как заряд упадет ниже 0,1, второй импульс вызовет срабатывание нейрона. Если второй импульс произойдёт позже, нейрон не сработает со вторым спайком. Хотя небольшой остаточный заряд может существовать, при соответствующем перекрестном подавлении с помощью синапсов с отрицательным весом можно получить группу нейронов каждый работающий на своей заданной входной частоте.

Этот метод реагирует не на количество импульсов за определенный период времени, а на временной интервал между двумя импульсами. Это означает, что мы не ограничены целым числом, кратным времени цикла нейрона. Например, если мы можем обнаружить сигнал с 4,0 мс между пиками, изменяя скорость утечки, мы можем также различить сигнал с 4,1 мс. Уровень сигнала обновляется каждые 2 спайка независимо от частоты входного сигнала. Без шума и с согласованными сигналами (ни одно из условий не существует в мозгу) можно было бы декодировать любую частоту срабатывания входного сигнала. Мы можем оценить временные интервалы между спайками, скажем, в интервале 4-5 мс с шагом 0,01 мс, то есть оценивать 100 уникальных значений при затратах в два нейрона на значение. Судя по наблюдениям за слуховым восприятием, количество обнаруженных уровней, вероятно, меньше десяти. 

Схема выше преобразует последовательный сигнал в параллельный набор каналов, каждый из которых соответствует определенной входной частоте. Нейрон «Input Changed» для каждого детектируемого уровня будет выдавать один спайк только при обнаружении заданного уровня. Если рассматриваемый сигнал исходил от фоторецептора палочки сечатки, чувствительного к интенсивности монохромного света, каждый из различаемых параллельных сигналов представлял бы определенный уровень серого в рассматриваемой точке.

Рассмотрим задачу обнаружения визуальной границы, на которую указывает разница в частоте импульсов между двумя соседними сигналами, которые могут быть не в фазе. Эта задача трудновыполнима при ограниченном времени на нейронах ИНС, причём обычно используется сверточный слой, не имеющий биологического аналога. С помощью описанного выше метода последовательно закодированный сигнал преобразуется в набор параллельных сигналов, по одному сигналу для каждого различного уровня сигнала. С этими параллельными сигналами определение существования границы становится вопросом определения того, активировался ли соответствующий нейрон уровня серого в каждом из двух соседних пикселей, и это легко достигается с помощью нейронных элементов AND.

Преобразование импульсного сигнала в частотный

Мышцы сокращаются сильнее в ответ на более частые импульсы двигательных нейронов. Импульсный сигнал легко преобразовать обратно в частотный, выбрав соответствующие веса синапсов, но модель LIF не может создавать сигналы с нецелочисленной частотой срабатывания (как описано выше). Однако было бы нетрудно расширить модель, чтобы позволить нейронам срабатывать с любой произвольной скоростью, если это окажется необходимым.

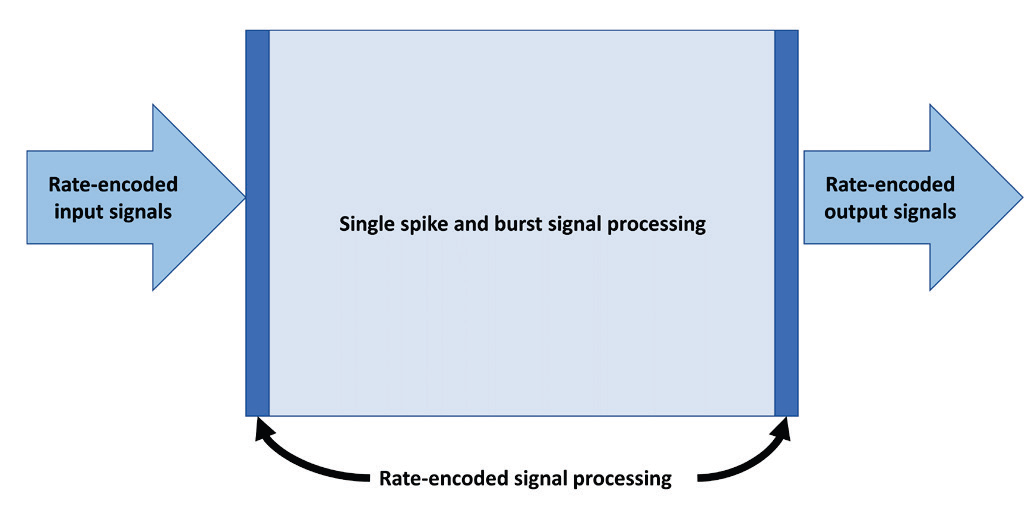
С точки зрения компьютерного проектирования можно увидеть, что входящие сигналы должны быть преобразованы в спайковые сигналы как можно раньше, вся обработка должна выполняться на параллельных одиночных импульсах, а выходные данные должны быть преобразованы обратно непосредственно перед выводом результата вычислений.

Здесь и далее под разметкой цитата “мой три копейки”, моё мнение и комментарии.

Чарльз Дж. Саймон во всей своей работе не упоминает о модулирующих синапсах. Это особый тип синапсов которые не влияет непосредственно на заряд мембраны нейрона, а меняет метаболизм клетки особым образам (Э. Кандел). К примеру, может повысить или понизить чувствительность клетки, или изменить время рефрактерного периода, или изменить синаптическую задержку, или сделать “Синапсы Хебба” (см. ниже) на некоторый период более пластичными. Многие нейронные схемы с применением данного типа синапсов можно было бы выполнить более компактно. К примеру, трансформацию частоты импульсов можно производить на одном моторном нейроне изменяя его порог активации (у Ч.Саймона он всегда равен 1) с помощью управляющего модулирующего сигнала. Подробнее о модулирующих синапсах я писал в этой статье (https://habr.com/ru/post/397375/) и пример практического применеия этой схемы.

Но главное в концепции модулирующих синапсов не в упрощении нейронных схем, а общем представлении того, как в мозге происходит переключение между различными “режимами”. К примеру, приятный запах выпечки больше окажет влияние на поведение голодного человека, чем сытого, запах определенно оказывает модулирующее действие на центры отвечающее за чувство голода, но не могут быть прямой причиной активности этих центров.

Одиночные импульсы

Поскольку нейроны с одиночными спайками представляют собой большинство нейронов в неокортексе, в этом разделе представлены некоторые методы обработки информации с использованием этой концепции. 

Механизм кратковременной памяти

Большинство систем ИНС полагаются на память, хранящуюся в синаптических весах. Хотя имеются существенные доказательства в пользу механизма памяти в изменении размеров синапсов, и он стабилен в течение длительного времени, но он имеет медленную скорость, требуя несколько циклов работы нейронов для сохранения изменений. Эти особенности делают память синаптического веса подходящей для долговременного хранения, но не для кратковременной памяти, на которую также полагается мозг. Цели разработки кратковременной памяти для модели мозга аналогичны задачам выполняемым ОЗУ: небольшое количество компонентов, низкое энергопотребление и высокая скорость чтения-записи.

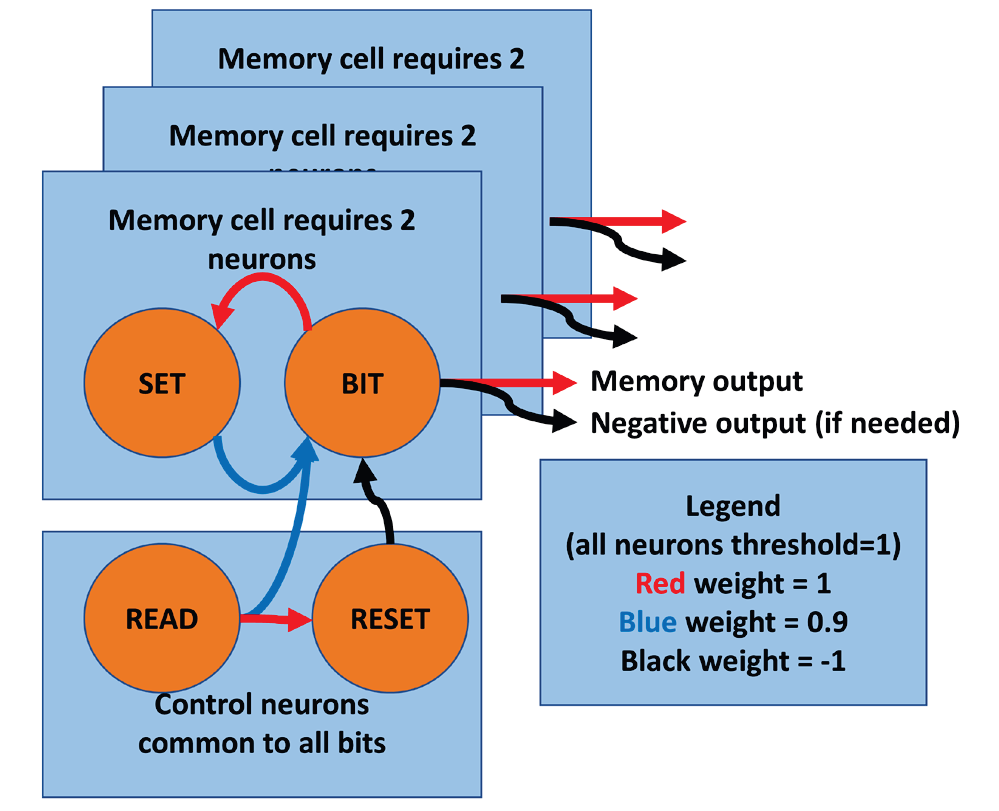
Механизм памяти, показанный на рисунке, состоит из двух нейронов на каждый бит памяти плюс два управляющих нейрона, общих для всех битов. Информация хранится на уровне внутреннего заряда нейрона BIT. Если нейрон SET срабатывает, он передает подпороговый заряд нейрону BIT, хранящему логическую единицу. Если сработает нейрон READ, сработает любой нейрон BIT с зарядом больше 0,1, генерируя выходной ответ. Одновременно он будет повторно стимулировать соответствующий нейрон SET, чтобы восстановить частичный заряд в нейроне BIT. Активация нейрона RESET сбросит заряд всех нейронов BIT.

Поскольку информация хранится в уровнях заряда нейронов, энергии не требуется, за исключением чтения и записи. Данные могут быть прочитаны сразу после записи, а повторные чтения могут выполняться каждые три нейронных цикла после этого. Данные накапливаются, поэтому входящие биты могут поступать в разное время. Любой RESET должен предшествовать любой записи по крайней мере на один нейронный цикл. Если нейроны являются типом IF, обновление информации не требуется, и память сохраняется неопределенно долго. Однако, если используется модель LIF, для сохранения информации необходимы периодические чтения, как и в случае с DRAM, и по тем же причинам. С другой стороны, при соответствующем значении утечки RESET может не понадобиться, поскольку память может исчезать с любой желаемой скоростью.

Эта схема кратковременной памяти настолько полезна и проста, что вполне вероятно, что у нее есть прямой аналог в мозгу.

Наконец, этот вид памяти может быть каскадным так, чтобы выходы одного набора нейронов передавались на входы SET следующего. Запуская RESET этапа n, за которым следует SET этапа n-1, данные передаются с этапа n-1 на этап n. Таким образом, может быть создан сдвиговый регистр кратковременной памяти любой желаемой скорости и глубины. С помощью соответствующих управляющих сигналов из такой кратковременной памяти можно считывать состояние входа в любой предшествующий момент времени на определенном интервале.

Очень упрощенное представление о памяти и стремление приблизить живой мозг к компьютеру приводят Чарльза Дж. Саймона к неким регистрам на нейронах. Это работает, но это не похоже на мозг. Изложу своё мнение. Три типа памяти и три вида её представления в мозге: моментальная память, кратковременная и долговременная. Моментальная память - память, которая действует очень короткий момент времени, позволяет нам набрать номер телефона пока его нам диктуют. Кратковременная память - память, которая может хранится некоторый ограниченный интервал времени минуты, часы, дни и даже недели, но обязательно будет утеряна если к ней повторно не обратится. И долговременная память - память которая сохраняется на неопределенное долгое время, зачастую на всю жизнь организма. 

Воплощением моментальной памяти в мозге являются реверберации, циклические передачи возбуждения между группой нейронов, зачастую между нейронами из разных отделов мозга или областей коры. Такие реверберации недолговечны что и определяет скоротечность моментальной памяти.

Особенность такой схемы в том, что не любой контур передачи может активироваться, между соседними контурами присутствует латеральное ингибирование (боковое торможение), что обеспечивает стабильную активность только одно контура из определённой группы - модуля, или гиерколонки. Размерность такой ячейки памяти определяет количество контуров в модуле. Четыре контура - всего четыре состояния, плюс неактивное состояние модуля. Это намного более энергетически затратная схема чем у Ч. Саймона, но очень стабильная в условиях шума и сбоев, которые свойственны для живой ткани.

Кратковременная память воплощена в MDMA-рецепторах (о них Ч. Саймон также не упоминает). Особый тип рецепторов нейромедиатора глутамата (обычно побудительного), которые изначально заблокированы ионом магния как пробкой. Чтобы выбить эти пробки из рецепторов нейрону необходимо многократно активироваться в короткий интервал времени, после чего нейрон становится значительно более чувствительным и легко активируется даже при относительно малом воздействии на него. Здесь прослеживается взаимосвязь между моментальной и кратковременной памятью, для активации MDMA-рецепторов требуется участие нейрона в стабильной реверберации. Но со временем ион магния может вернутся в MDMA-рецептор опять заблокировав его.

Долговременная память воплощена в изменении синаптических шипиков и росте/деградации новых отростков. Подобные перестройки требуют времени, в течении 20 минут у нерона может появится полноценный новый отросток с новыми синаптическими контактами. В отличии от неMDMA-рецепторов, MDMA пропускает ионы кальция а не калия, и скорее всего, эти ионы и запускают инициацию изменений в нейроне, так прослеживается связь между временной и долговременной памятью. Для координации изменений в нейроне служат белки прионы, они выступают в роли маркеров, так как могут локально в теле клетки поддерживать свою концентрацию, например, помечая нужный синапс или отросток. Поэтому при необходимости нейрон может “запланировать” некоторые изменения в своей архитектуре уже при однократном акте обучения и выполнить их позже с течением времени. 

Но это всё не умаляет работу Ч. Саймона, строгость компьютерной модели дает возможность строить память по иным принципам нежели в биологической нервной системе.

Нейронная логика с низким энергопотреблением

На рисунке показан вариант логической схемы, который может выполнять функции логических элементов с гораздо меньшими энергетическими затратами. Кратковременная память на входе означает, что входы A и B могут поступать асинхронно. Когда срабатывает нейрон  READ, различные выходные сигналы будут выдавать один спайк (или нет в зависимости от ситуации). В остальное время нейроны не срабатывают.

Эта схема устраняет необходимость в постоянном срабатывании логических схем, поскольку она работает с отдельными импульсами. По сути, это определяет новое логическое семейство, в котором логическая 1 представлена одним импульсом в любой момент времени, а 0 представлена отсутствием какого-либо сигнала. 

Это логическое семейство использует энергию только при расчете состояний выходов.

Нейронный граф

С помощью нейронных схем, которые преобразует потоки импульсов в отдельные спайки, схем кратковременной памяти и различных логических функций, входящие нейронные сигналы могут обрабатываться для определения визуальных границ, изменений слухового ввода и т. д. Например, можно ожидать, что отдельные нейроны в зрительной коре выдают отдельные импульсы в ответ на линии, углы, дуги и цвета. Различные нейроны излучают отдельные спайки в ответ на обнаруженные звуки или изменения высоты тона или громкости, другие нейроны срабатывали в ответ на определенные прикосновения, вкусы и ароматы.

Эти отдельные импульсы могут иметь определенное значение, например, один спайк может передавать определенный цвет в определенном видимом месте или звук одной фонемы. Как использовать такие импульсы для выполнения полезных функций ИИ? В этом разделе показано, что структурированные данные могут храниться в синапсах, соединяющих “одноимпусные” нейроны.

Например, после некоторого обучения общий ИИ должен уметь читать и понимать произносимые слова и отвечать на вопрос: «Что такое синий?» - «Синий — это цвет», «Какие бывают цвета?» - «Синий, красный и зеленый», «Какая фраза содержит «маленький ягненок?»» - «У Мэри был маленький ягненок». Кроме того, сильный ИИ должен объединять информацию от органов чувств, чтобы слова можно было использовать для описания видимых, слышимых или осязаемых объектов, а входящие слова могли запускать воображаемые образы объектов. Эти способности есть у любого ребенка.

В оставшейся части этого раздела обсуждается структура, созданная с помощью смоделированных нейронов LIF, которая может выполнять эти задачи. Поскольку эта структура может выполнять многие из тех же интеллектуальных задач, что и мозг, вероятно, в мозгу есть аналогичная структура. Поскольку такой структуры не наблюдалось, можно предположить, что данная функциональность распределена по всему неокортексу.

Структура нейронного графа

Предлагаемый здесь ответ представляет собой математический граф, созданный из нейронов LIF. Граф — это структура, содержащая узлы, соединенные ребрами. Это приблизительно аналогично набору нейронов, соединенных синапсами, но в описанной здесь реализации для каждого узла требуется семь или более нейронов с несколькими синапсами, а также несколько управляющих нейронов.

Рассмотрим прямоугольный массив нейронов, каждая строка которого представляет собой узел графа. Каждый узел имеет часть схемы кратковременной памяти в качестве входных данных, поэтому входные данные могут поступать асинхронно. Если бит памяти отличен от нуля, мы будем считать узел «активированным». Каждый узел имеет на выходе также схему кратковременной памяти. Отдельные выходные нейроны необходимы, чтобы на графе можно было различать «синий» на входе и «синий» на выходе.

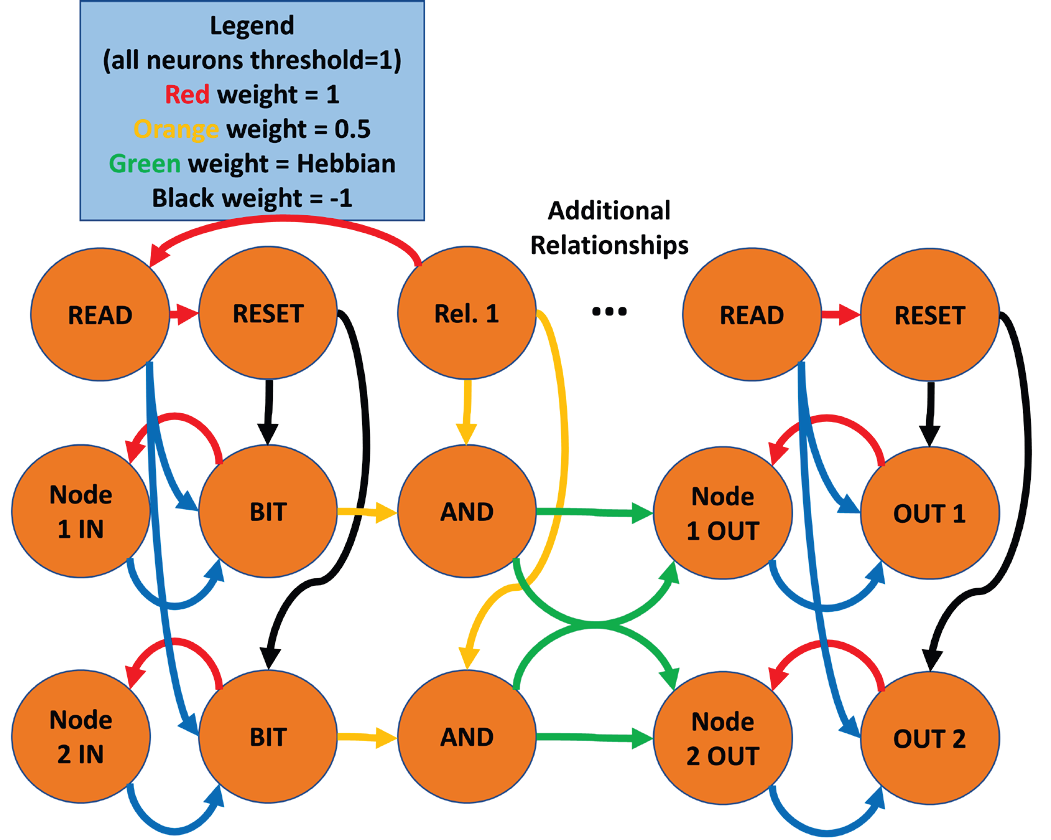
Дополнительные столбцы в массиве представляют дополнительные типы связей, и между активацией и управляющим сигналом есть нейронные элементы AND, которые являются общими для всех узлов в столбце.

В качестве примера рассмотрим связь родительский-дочерний, которая обычно используется для представления отношений типа «это является этим». Поскольку синапсы являются однонаправленными, Родительский и Дочерний являются отдельными отношениями. Если три узла представляют “КРАСНЫЙ”, “СИНИЙ” и “ЦВЕТ”, “КРАСНЫЙ”-родительский нейрон будет иметь исходящий синапс, соединяющий его с узлом “ЦВЕТ” и аналогично для узла “СИНИЙ”. Нейрон “ЦВЕТ”-дочерний будет иметь входящие синапсы с узлами “КРАСНЫЙ” и “СИНИЙ”.

Чтобы задать родительский узел для “КРАСНЫЙ”, активируйте “КРАСНЫЙ” нейрон и запустите нейрон ответственный за Родительский (Parent) тип связи, совместная их активация создаст между ними связь. В последующем активация Parent нейрона активирует выходы всех узлов, которые были сохранены как родительские.

Синапс Хебба

До этого момента синапсы были фиксированные как по весу, так и по местоположению. В модели некоторые синапсы могут быть обозначены как «Хеббовские». Хеббовские синапсы увеличивают свой вес, если их нейроны-источники и нейроны-мишени срабатывают в одном и том же цикле. Биологические хеббовские синапсы изменяют свой вес либо положительно, либо отрицательно в зависимости от временных соотношений возбуждения исходного и целевого нейронов. 

Изначально все хеббовские синапсы имеют значение 0. Если в графе N узлов, то для каждой связи имеется N2 хеббовских синапсов. При весе 1 эти синапсы представляют наличие связи, а при 0 — отсутствие. Промежуточные значения могут отражать силу связи.

Хранение информации в графе

Чтобы сохранить связь в графе, сначала активируйте целевой узел и запустите нейрон “ЭТО”, чтобы передать его на выход. Затем активируйте исходный узел и запустите нужный нейрон типа связи. Узел типа связи, логический AND и выход могут сработать одновременно, и синапс, соединяющий их, укрепится. 

Например, чтобы установить “ЦВЕТ” в качестве родителя “СИНЕГО”: активируйте “ЦВЕТ”, активируйте “ЭТО”, активируйте “СИНИЙ”, активируйте “РОДИТЕЛЬ” и выходной нейрон одновременно.

Хотя этот процесс может показаться слишком сложным для существования в биологических условиях, рассмотрим минимальные требования. Должен существовать массив нейронов, полностью связанных между собой синапсами Хебба. Затем два нейрона, представляющие  вершины связи, должны активироваться более или менее одновременно, чтобы усилить синапс. Этот минимальный механизм должен существовать в мозгу. Нейронный Граф добавляет возможность обрабатывать асинхронные сигналы и несколько типов родства в одном массиве.

Дополнительный типы отношений

В дополнение к отношениям Родительский, Дочерний и Это необходимо еще несколько. Например, рассмотрим физический объект, который хранится с несколькими атрибутами, такими как размер, форма и цвет. Большой синий квадрат будет представлен одним узлом с отношениями атрибутов с узлами БОЛЬШОЙ, СИНИЙ и КВАДРАТ. Другой узел будет представлять собой маленький красный кружок с другими отношениями атрибутов. Обратные отношения атрибутов также необходимы для того, чтобы структура могла вспомнить не только то, что конкретный объект является синим, но и вспомнить другие объекты того же цвета.

Здесь мы видим пример того как Чарльз Дж. Саймон на базе своих моделей нейронов предлагает некую структуру памяти - Нейронный Граф. Сам граф проявляется как некое эмерджентное свойство, для его проявления необходимо организовать определенным образом сеть нейронов. Узлами графа будут являться некие репрезентации, представления образов в виде активности конкретных нейронов. Рёбра графа взвешены и имеют различные типы, к примеру, тип родитель, тип дочерний, тип “это”. Рёбра могут быть однонаправленными и двунаправленными. 

Для многих очевидно, что человеческие знания можно представить в виде графа и стоит отдать должное Ч. Саймону он описывает как этот граф может быть связан непосредственно с нейронами.

Множество нейронных графов

16 миллиардов нейронов неокортекса предполагают возможность нейронного графа с максимум, возможно, миллиардом узлов. Однако обычно наблюдается, что биологические нейроны имеют от 1000 до 10000 синапсов. Это ограниченное предполагает архитектуру, которая ограничивает размер отдельного нейронного графа с полным хранилищем знаний мозга, разделенным на несколько графов, некоторые из которых параллельны, а другие связаны последовательно. Экспериментально это не реализовано.

Наблюдаемое время реакции также ограничивает количество узлов, которые могут быть последовательно соединены. Как правило, любая связь в нейронном графе декодируется за шесть нейронных циклов (дольше для неточных совпадений). Чтобы среагировать за 0,1 с, при задержке распространения возбуждения по нейрону в 5 мс, такой сигнал пришлось бы декодировать всего на трех последовательных уровнях. Эти цифры, хоть и правдоподобны, иллюстрируют ограниченность архитектуры. Когда человек читает текст, например, несколько последовательных графов создают конвейерную архитектуру, и если для обработки смысла требуется тридцать уровней графа, можно иметь высокую скорость чтения, но смысл не будет полностью декодирован в течение целой секунды после восприятия зрительной корой формы букв. Это также правдоподобно.

Можно было бы ожидать, что граф, который принимает визуальные примитивы и распознает символы, будет отдельным и параллельным графу, который принимает входящие слуховые примитивы и распознает фонемы.Такой подграф может не нуждаться в полном наборе отношений, а может иметь только те, которые необходимы для поиска атрибутов.

Выходы графа распознавания букв станут входными данными для графа распознавания слов, и это будет параллельно графу распознавания слов на слух. Можно также сделать вывод, что словарный запас человека содержит слишком много слов, чтобы их можно было хранить в отдельном графе, и что необходимо несколько параллельных графов.

В какой-то момент распознанные слуховые и визуальные потоки слов сливаются. Обратные атрибуты явно необходимы, потому что, когда люди читают, они могут «слышать» слова в уме. Кроме того, когда кто-то слышит слово, ум может проследить обратные атрибуты, чтобы узнать, как пишется слово.

Последовательная информация

Пример физических объектов и их атрибутов представлен атрибутами, которые одновременно имеют значение, и это возможно, потому что, когда нейрон срабатывает, все синапсы передают заряд нейронам-мишеням более или менее одновременно. Для данных, которые требуют извлечения в определенном порядке, все становится сложнее. Большая часть информации в человеческом опыте упорядочена: слова во фразах, фонемы в словах, написание, числа, визуальная информация упорядочена по вертикали и горизонтали и т. д.

Если бы фраза «Быть или не быть» хранилась бы в одном узле со связями атрибутов с четырьмя узлами слов, слова извлекались бы одновременно или в случайном порядке без учета повторяющихся слов.

Для хранения последовательных данных в Нейронном Графе для каждого шага в последовательности были выделены отдельные узлы, связанные отношением Next. Каждый узел шага имеет атрибутивную связь с определенным узлом слова. Чтобы воспроизвести фразу, активируется первый узел последовательности, и повторное срабатывание отношения NEXT будет выводить слова в последовательности. Для поиска фразы, когда получено начальное слово, все сохраненные узлы шагов, ссылающиеся на это слово, будут активированы. Когда будет получено следующее слово, оно активирует только узлы с этим словом и связью Next с предыдущего активного шага.

Родительский узел последовательности шагов соединен с первым узлом последовательности, поэтому, если будет найдено частичное совпадение с последовательностью, можно будет найти начало последовательности. То есть при вводе «не быть» граф может найти начало и воспроизвести всю последовательность «быть или не быть».

Механизмы поиска и извлечения были реализованы экспериментально на основе последовательностей, вручную закодированных в Нейронный Граф. Никаких экспериментов по хранению последовательной информации в Нейронном Графе не проводилось.

С помощью этого метода любая последовательность требует количества узлов, длине ее, но можно увидеть, как каскадные последовательности последовательностей (а не последовательности слов) могут использоваться для хранения информации произвольной длины с ограниченной длиной отдельной последовательности. То есть при запоминании любого текста короткие фразы (последовательности слов) объединяются в общий граф (последовательность этих последовательностей). Неподтвержденные данные свидетельствуют о том, что индивидуальная последовательность в мозге ограничена примерно семью шагами.

Можно заметить, что последовательная информация поразительно менее эффективна, чем параллельная. Можно сохранить изображение лица с пятьюдесятью атрибутами с одним нейроном и пятьдесят синапсов со значениями связанных атрибутов. Для хранения последовательности из пятидесяти слов теоретически потребуется не менее пятидесяти нейронов, а в этой реализации — не менее 350 нейронов (семь нейронов на узел). В этом примере хранение 50 атрибутов более эффективно, чем последовательное с соотношением 350:1.

Нет данных в Нейронном графе

В Нейронном Графе, в отличие от большинства других графических программ, нет данных, только связи между узлами. Узлы имеют значение только в контексте других узлов и соединений с входами или выходами. Один узел может представлять слово «красный», но узел не имеет внутреннего значения, поскольку это всего лишь один бит. Его значение полностью выводится из связей, которые оно имеет с последовательностью фонем, с помощью которых можно услышать и произнести слово вслух, последовательностью букв, позволяющей читать и писать слово, и отношениями с абстрактным узлом “КРАСНЫЙ”, который активируется, когда сетчатка видит цвет. Он также связан с множеством фраз, в которых используется это слово, и, таким образом, связан с другими словами, имеющими собственный контекст и абстрактное значение.

Следовательно, даже если отдельные узлы не имеют внутреннего значения, синапсы, которые представляют отношения, реализуют значение, которое может быть чрезвычайно устойчивым.

Реализация

Большая часть описанных схем требует определенного времени, критических весов синапсов и может выйти из строя с потерей одного синапса. В мозге синхронизация явно более зашумлена, и мозг может продолжать нормально функционировать с потерей многочисленных компонентов. Можно предположить, что мозг приобретает свою надежность за счет значительных дополнительных нейронных цепей.

Минимальный нейронный граф требует как минимум семь нейронов: четыре для управления вводом и выводом и три для отслеживания состояния «используется/свободен». 14 синапсов, необходимых в узле, не имеют существенного значения для производительности. Каждая связь добавляет один нейрон на узел, и этот нейрон имеет синапсы со всеми другими узлами в графе. Для полноценного Нейронного Графа из N узлов с шестью типами отношений требовалось 15 нейронов на узел и 6N2 синапсов.

Шум и избыточность

Компьютерное моделирование практически не содержит ошибок и помех. Не требуется никаких поправок на возможный отказ отдельных нейронов и синапсов или даже значительных блоков. Схемы, определенные здесь, работают только в бесшумной среде, и для того, чтобы сделать их устойчивыми к шуму, потребуется существенная доработка. Не делается оценок того, какая дополнительная сложность потребуется для соответствия отказоустойчивости и устойчивости мозга к помехам.

Непосредственный вес синапса

Регулировка веса биологического синапса Хебба происходит небольшими шагами, требующими всплесков спайков для изучения веса. Компьютер может установить любой вес синапса напрямую. Например, обучение в нейронном графе можно выполнить за один или два цикла, установив таблицу веса обучения.

Универсальное хранилище знаний (UKS)

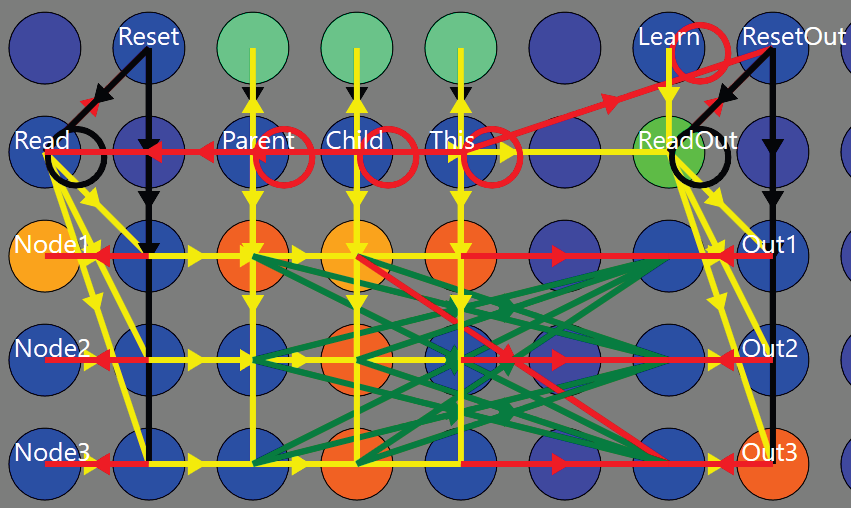
Работа с возбуждением отдельных нейронов в нейронном графе становится все более сложной для отладки по мере роста графа, и аналогичный механизм графа был реализован на языке более высокого уровня (C#), это Универсальное хранилище знаний (UKS). При подключении к входным и выходным нейронам аналогично Нейронному Графу, этот граф использует внутренние языковые структуры высокого уровня.

Эта реализация также имеет диалоговое окно, которое может отображать содержимое графа в виде древовидной структуры, и другое, которое показывает, какие узлы активированы снаружи и внутри. Кроме того, реализовано несколько методов поиска. Не проводилось никаких измерений, чтобы определить, что быстрее — UKS или Нейронный Граф (Neural Graph), но версия C# намного проще в разработке.

UKS взаимодействует с внешней схемой с массивами входных и выходных нейронов точно так же, как Нейронный Граф. В UKS управляющие синапсы нейронного графа заменены несколькими строками кода. Приложение UKS, изображенное на рисунке ниже, использует узлы для представления фонем, слов и фраз. Как и в нейронном графе, в UKS не хранятся никакие данные, а узлам присваиваются произвольные метки, за исключением тех, которые связаны с известными входами и выходами. Как показано на рисунке, фраза ph7 состоит из слов w3, w4 и w2 (именно в таком порядке). Слова связаны с фонемами, которые, в свою очередь, связаны с речевым движком. Приложение получает непрерывные потоки фонем и может определять слова и фразы с повторением.

UKS также может обрабатывать пространственные отношения, атрибуты физических объектов, ориентиры, фонемы, слова, фразы и может быть расширен для добавления любой информации. Таким образом, он обеспечивает механизм хранения знаний, который можно применить к любой модели AGI.

Узлы в UKS являются абстрактными, но могут включать в себя другие данные для быстрого доступа к программированию. Например, близлежащие объекты сохраняются с полярными векторами, указывающими их расстояние и азимут. Это откладывает разработку нейронной схемы (или узлов UKS) для обработки этой информации. В мозгу аналогичной способностью обладают Grid Cells. UKS также может объединять информацию из нескольких источников ввода, поэтому свойства внешнего вида видимого объекта естественным образом сливаются со словами словесного описания.

Диалоговое окно представляет UKS в виде дерева. Но технически структура не является деревом, потому что она поддерживает несколько родителей и может иметь циклические ссылки.

Веса соединений использовались для изучения ассоциаций одновременных активаций. Например, слова будут иметь малозначительную связь атрибутов со всеми узлами, которые были активированы в то время, когда слово было услышано. С каждым последующим прослушиванием эти веса увеличиваются, и со временем слова будут иметь наибольший вес, связанный с вещами, к которым они относятся, и ошибочный ввод в конечном итоге будет отфильтровываться. После того, как такая специфическая корреляция установлена, маловесные связи могут быть удалены.

Моделирование некоторых структур памяти основанное на нейронах помогло Ч. Саймону выделить некий общий алгоритм формирования знаний в мозге и реализовать его без нейронов. Это сильно упростило работу с этими структурами и сохранило возможность совместной работы и интеграции UKS с симуляцией нейронов. То есть Симулятор мозга II позволяет использовать Нейронный Граф без необходимости строить большую сеть определенным образом организованных нейронов и при этом работать с отдельными нейронами. Весьма верное решение с точки зрения удобства и экономии вычислительных ресурсов.

Заключение и будущие исследования

В этой статье предлагается новое направление исследований ИИ, отличное от ИНС/обратного распространения, но более общее и нейроморфное, чем обычно узкие символические подходы ИИ. Схема кратковременной памяти и маломощная цифровая нейронная логика предлагают механизмы, которые могут создать любую желаемую нейронную функциональность. Нейронный Граф (Neural Graph) и Универсальное хранилище знаний (UKS) обрисовывают в общих чертах механизмы, которые объединяют информацию от нескольких органов чувств и имитируют функциональные возможности, рассматриваемые как основные для интеллекта. Вместе они составляют основу больших областей будущих исследований ИИ.

В ближайшем будущем эксперименты с большими наборами данных должны расширить возможности и предоставить более конкретные данные о производительности.

---

Идеи и взгляды Чарльза Дж. Саймона на проблематику оказались для меня очень близки. За последнее время его компания получила сильное развитие, обновлен сайт, выпущен ряд новых видео на ютуб-канале. За этим развитием интересно следить, поэтому welcome.