Глупость ведёт к потерям. Конец предисловия.
Почему так хочется уметь делить на ноль? Потому что очень хочется всегда уметь возвращаться.
Математический запрет деления на ноль — запрет на потакание глупости. Вы уменьшили степень числа до бесконечно отрицательной, практически выкинули точное значение, чего же вы теперь хотите? Нельзя рассчитывать вернуться там, где это исключено. Хорошо, что существуют числа, очень похожие на ноль, но не являющимся им. Можно надеяться, что тот ноль, на который вы умножили — был из таких подделок, и можно всё вернуть. Но, такие нули слабенькие — с числами масштаба обратных они не справятся.
Ещё один пример глупости — это закрыться в сейфе, вместе с единственными ключами. Кто так делал — авторитетно вам расскажет, что в таком случае без машины времени не обойтись. Очень хотелось бы иметь машину времени на такой случай. Другое дело, что машина времени существует в доступном виде — в виде разума и понимания, что так делать не стоит. Осталось эту машину времени повсеместно применить. Просто, лучше применять её до того как она понадобится.
Возьмём для дальнейшего рассказа умножение числа на само себя. Этот процесс вполне можно обратить. Но, одна частица у числа всё же потеряется — это знак. Чтобы вернуть число из полученного, нужно будет позаботиться о том, чтобы во время таких качелей информация о знаке исходного числа где-то лежала, хранилась, и при возвращении надеяться, что тот знак, который нам вернули с сохранения — тот же, что мы на сохранение отдавали.
А что будет, если вернуть первоначальное число из такого значения, в котором знак не потерян? Получится ли вычислить корень из отрицательного числа? Разумеется, вам точно так же придётся что-то восстанавливать — у результата вычисления корня точно так же два варианта. Но если действительно получится восстановить, то значит, исходное число — это что-то такое, что потеряло вовсе не ту часть, которая теряется у обычного числа. Так что, исходное число сильно отличается от обычных — при возведении в квадрат становясь обычным, оно теряет совсем другую часть. Но, даже при своём отличии, оно существует с такой же бедой — без потери не обходится.
Общий принцип противостояния глупости — не делать необратимых поступков, или хотя бы обеспечить, чтобы способ возвращения существовал. Только, зачем противостоять, если можно изучить извне? Давайте не будем делать глупостей, только поговорим о них? Произведём искусственную глупость в лабораторных условиях и посмотрим на неё со стороны.
Матрица — описанные необычные числа можно представить в виде двумерных сеток обычных чисел. Умножение матриц достаточно простое — для получения числа в некоторой клеточке нужно сложить получающиеся произведения, пробежавшись в одной исходной матрице по той же строке, а в другой матрице по той же колонке. Только, выбор по какой из них в каком направлении бежать, влияет на результат, поэтому становится важным, какая матрица слева, а какая справа. А если исходные матрицы по форме одинаковые, но не квадратные, то одна из них при умножении должна быть повёрнута, и полученная матрица всё равно станет квадратной. Не-квадратность в таком произведении теряется — одной невосполнимой потерей больше.
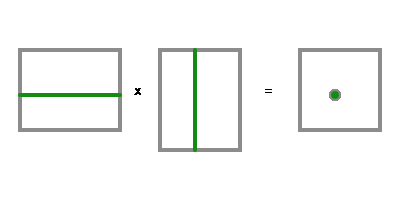 Матрица
Матрица ![$\small\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$]() — это единица в матричном представлении. И отрицательная единица
— это единица в матричном представлении. И отрицательная единица ![$\small\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$]() вполне переходит в единицу при возведении в квадрат.
вполне переходит в единицу при возведении в квадрат.
Матрицы![$\small\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$]() и
и ![$\small\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$]() переходят в эту отрицательную единицу при возведении в квадрат, так что вместе могут представлять собой то особое число — мнимую единицу, и её знаковую противоположность.
переходят в эту отрицательную единицу при возведении в квадрат, так что вместе могут представлять собой то особое число — мнимую единицу, и её знаковую противоположность.
Рзберём это в общем виде.
Для матрицы![$\small\begin{bmatrix} a & b \\ c & d \end{bmatrix}$]() результат возведения в квадрат это
результат возведения в квадрат это ![$\small\begin{bmatrix} aa+bc & ab+bd \\ ca+dc & cb+dd \end{bmatrix}$]() .
.
И если мы хотим этим действием получить обычное число![$\small\begin{bmatrix} x & 0 \\ 0 & x \end{bmatrix}$]() , то нужно решить систему уравнений
, то нужно решить систему уравнений
![$a^2 = d^2 = x - bc$]() , есть квадраты, а значит, возможно как совпадение так и различие знака.
, есть квадраты, а значит, возможно как совпадение так и различие знака.
Во втором равенстве,![$b(a+d)=c(a+d) = 0$]() , условия верности могут быть на выбор: либо
, условия верности могут быть на выбор: либо ![$a + d = 0$]() , либо
, либо ![$b = c = 0$]() .
.
Когда верно только![$a + d = 0$]() , то получается, что величины
, то получается, что величины ![$a^2$]() и
и ![$d^2$]() могут отличаться от
могут отличаться от ![$x$]() .
.
Матрица![$\small\begin{bmatrix} n & (x-n^2)/m \\ m & -n \end{bmatrix}$]() или
или ![$\small\begin{bmatrix} n & (\sqrt{x-n^2})/m \\ (\sqrt{x-n^2})m & -n \end{bmatrix}$]() в квадрате даёт
в квадрате даёт ![$\begin{bmatrix} x & 0 \\ 0 & x \end{bmatrix}$]() .
.
Ого — теряется уже не знак. Теряются две величины,![$n$]() и
и ![$m\;$]() .
.
И можно отметить, что случаи![$n^2 = x$]() и
и ![$n^2 = 0$]() можно разделить, но их смесь точно также будет выполнять равенство.
можно разделить, но их смесь точно также будет выполнять равенство.
![$\varphi$]() .
.
Вывернем квадрат наизнанку и посмотрим, что значит корень.
Плюс/минус слева говорит, что существует корень из единицы, не равный ни единице, ни минус единице. С учётом знака, их даже два. А с правой частью что?
Видимо, чтобы при вычислении корня были получены любые матрицы, нужно предусмотреть добавление произвольной величины, которая этим способом не достигается. Соответственно, и вычисление квадрата теряет эту информацию. Как будто существования шести различных корней из единицы, без учёта сочетаний (![$\varphi$]() ) и дисбалансированных значений (
) и дисбалансированных значений (![$m$]() ), было для учёта потерь недостаточно.
), было для учёта потерь недостаточно.
Дальше можно попробовать обобщить, сначала чтобы элементы матриц тоже были матрицами, затем на гильбертово пространство. Но статья не о математике, вы ж понимаете?
— Как редактору, мне надо бы сделать автору замечание, что начинается текст слишком издалека, примитивно и абстрактно, можно сказать, заумно — Но как графоману, мне безразлично. — Пишешь про деление на ноль? Точно графоман. — Про желание избежать потерь.Берём число, уменьшаем в два раза, получаем другое число. Потом говорим «Ха-ха, это шутка», умножаем полученное число на два, получаем третье число, которое восхитительно равно первому. Всегда можно вернуться. Или, берём число, умножаем на ноль. Говорим «ха-ха, сейчас всё вернём». Ищем на что бы такое умножить, чтобы вернуть, и не находим. Ну вот, вернуться не получается. Умножать на ноль было достаточно глупо.
Почему так хочется уметь делить на ноль? Потому что очень хочется всегда уметь возвращаться.
Математический запрет деления на ноль — запрет на потакание глупости. Вы уменьшили степень числа до бесконечно отрицательной, практически выкинули точное значение, чего же вы теперь хотите? Нельзя рассчитывать вернуться там, где это исключено. Хорошо, что существуют числа, очень похожие на ноль, но не являющимся им. Можно надеяться, что тот ноль, на который вы умножили — был из таких подделок, и можно всё вернуть. Но, такие нули слабенькие — с числами масштаба обратных они не справятся.
Ещё один пример глупости — это закрыться в сейфе, вместе с единственными ключами. Кто так делал — авторитетно вам расскажет, что в таком случае без машины времени не обойтись. Очень хотелось бы иметь машину времени на такой случай. Другое дело, что машина времени существует в доступном виде — в виде разума и понимания, что так делать не стоит. Осталось эту машину времени повсеместно применить. Просто, лучше применять её до того как она понадобится.
Возьмём для дальнейшего рассказа умножение числа на само себя. Этот процесс вполне можно обратить. Но, одна частица у числа всё же потеряется — это знак. Чтобы вернуть число из полученного, нужно будет позаботиться о том, чтобы во время таких качелей информация о знаке исходного числа где-то лежала, хранилась, и при возвращении надеяться, что тот знак, который нам вернули с сохранения — тот же, что мы на сохранение отдавали.
А что будет, если вернуть первоначальное число из такого значения, в котором знак не потерян? Получится ли вычислить корень из отрицательного числа? Разумеется, вам точно так же придётся что-то восстанавливать — у результата вычисления корня точно так же два варианта. Но если действительно получится восстановить, то значит, исходное число — это что-то такое, что потеряло вовсе не ту часть, которая теряется у обычного числа. Так что, исходное число сильно отличается от обычных — при возведении в квадрат становясь обычным, оно теряет совсем другую часть. Но, даже при своём отличии, оно существует с такой же бедой — без потери не обходится.
Общий принцип противостояния глупости — не делать необратимых поступков, или хотя бы обеспечить, чтобы способ возвращения существовал. Только, зачем противостоять, если можно изучить извне? Давайте не будем делать глупостей, только поговорим о них? Произведём искусственную глупость в лабораторных условиях и посмотрим на неё со стороны.
Матрица — описанные необычные числа можно представить в виде двумерных сеток обычных чисел. Умножение матриц достаточно простое — для получения числа в некоторой клеточке нужно сложить получающиеся произведения, пробежавшись в одной исходной матрице по той же строке, а в другой матрице по той же колонке. Только, выбор по какой из них в каком направлении бежать, влияет на результат, поэтому становится важным, какая матрица слева, а какая справа. А если исходные матрицы по форме одинаковые, но не квадратные, то одна из них при умножении должна быть повёрнута, и полученная матрица всё равно станет квадратной. Не-квадратность в таком произведении теряется — одной невосполнимой потерей больше.

Матрицы
Рзберём это в общем виде.
Для матрицы
И если мы хотим этим действием получить обычное число
Во втором равенстве,
Когда верно только
Матрица
Ого — теряется уже не знак. Теряются две величины,
И можно отметить, что случаи
Вывернем квадрат наизнанку и посмотрим, что значит корень.
Плюс/минус слева говорит, что существует корень из единицы, не равный ни единице, ни минус единице. С учётом знака, их даже два. А с правой частью что?
Видимо, чтобы при вычислении корня были получены любые матрицы, нужно предусмотреть добавление произвольной величины, которая этим способом не достигается. Соответственно, и вычисление квадрата теряет эту информацию. Как будто существования шести различных корней из единицы, без учёта сочетаний (
Дальше можно попробовать обобщить, сначала чтобы элементы матриц тоже были матрицами, затем на гильбертово пространство. Но статья не о математике, вы ж понимаете?


pepelnyy
Не хватает знаний и ума, чтобы понять фактическую часть. Но язык! Пишите ещё!