На прошлом витке чего-о?

Изобрёл плоскостные числа — у нас они называются комплексными. Выдвинул гипотезу о знаке, что числа могут быть не только положительными и отрицательными, но и ещё, подобно тому как можно двигаться на плоскости не только вперёд и назад, но и вправо и влево — числа тоже могут быть расположены в других направлениях. В конце своей жизни Эскобар разочаровался в математике, да и вообще во всём. И в нашем витке времени он стал музыкантом. И никто бы не узнал, что он в душе математик, если бы на одном из концертов у него не взяли интервью, где в ответ на предложение сравнить два варианта он категорически выдал свою гипотезу за аксиому: двух вариантов недостаточно.
Комплексные числа были открыты без участия Эскобара, но это не значит, что мы должны отказываться от его наследия. Все знают, что 2+2=4, 2×2=4, 2^2=4. Только, при возведении в степень существует разница в порядке аргументов. Что если применить гипотезу Эскобара на нашем убеждении, что у порядка при возведении в степень может быть только два варианта? Ну а вдруг — больше?
Степень
Тексты у нас чисто сугубо психологические и возникают спонтанно.Люди давно знали что такое степень. Ещё бы, замена произведения чисел на сложение степеней превращает сложную операцию в лёгкую. Дело остаётся за малым: быстро переводить из числа в степень и обратно. Пришлось изобретать логарифм.
Смущало только два момента: что у нуля степень уходит в минус бесконечность, а у единицы степень равна нулю. Поэтому ноль так долго не хотели открывать, а единицу так вообще за число не считали. Но ведь отрицательные числа и отрицательные степени положительных чисел меньше единицы вполне согласованы, в чём дело?
Опасность проявлялась в том что умножение на ноль на уровне степеней уменьшала любую степень до бесконечно отрицательной. И что самое горькое: её нельзя вернуть обратно. Делить ноль на ноль это все равно что говорить: «не знаю». Надо было бы как-то постараться заранее сделать резервную копию того что вы собираетесь на ноль умножить, и не терять.
Это не единственная потеря в математике. Умножение числа на себя это всё равно что возводить число во вторую степень. Вернуть обратно число можно, вычислив корень, как степень одна вторая. Но отрицательные числа в квадрате будут положительными, и если возвращать обратно, то нужно кое-что постараться вспомнить о числе, то что потерялось, знак.
В целом, это не проблема — всего два варианта. Но, что если кроме положительных и отрицательных чисел есть и такие числа, которые в квадрате дают отрицательные? Знак-то, может, и теряется, но — тот который был, а не тот который стал.
Точки на плоскости намекают: поворот может быть степенью, увеличить степень в два раза может быть просто удвоенным поворотом. А значит, такие числа не только существуют, вторая составляющая это полноценный дубль первой составляющей, и у них прекрасная связь.
И конечно же, при вычислении корня таких комплексных чисел ровно два, знак теряется точно так же.
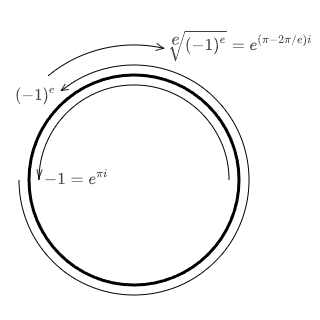
Так как аналогия с поворотом проста, то спокойно можно возводить любое комплексное число в любое комплексное число. Только, поворот имеет свойство повторять на следующих оборотах то же что было на предыдущих, и поэтому теряться может гораздо больше, чем просто знак. И если показатель у степени обратный, то происходит и ещё кое-что обратное: значение придётся восстанавливать.
Например, если минус один возвести в степень
Матрицы
Это не есть, так сказать, музыка.Пересчёт набора координат в другой набор осуществляется умножением матриц, в виде произведения матрицы пересчёта и вектора значений. Сами пересчёты можно комбинировать, тоже через умножение матриц. Правила умножения такие: для вычисления числа в некоторой клеточке нужно сложить получающиеся произведения, пробежавшись в одной исходной матрице по той же строке, а в другой матрице по той же колонке. Только, выбор по какой из них в каком направлении бежать влияет на результат, поэтому становится важным, какая матрица слева, а какая справа.
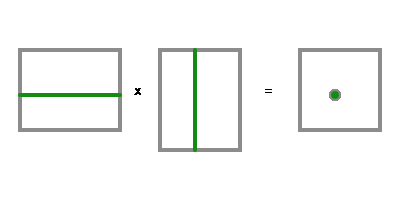
Среди матриц есть аналог обычного числа. Это квадратная матрица, у которой это число расставлено по диагонали. И если такую матрицу умножить на вектор, то будет тот же вектор, умноженный на это число.
У единицы есть свой аналог,
Интересно было бы посмотреть, а что возведение в квадрат теряет. Разберём это в общем виде.
Для матрицы
И если мы хотим этим действием получить обычное число
Во втором равенстве,
Когда верно только
Например, матрица
Ого! — теряется уже не знак. Теряются две величины,
И можно отметить, что случаи
— При любом
Вывернем квадрат наизнанку и посмотрим, что значит корень.
Плюс/минус слева говорит, что существует корень из единицы, не равный ни единице, ни минус единице. С учётом знака, их даже два. А с правой частью что?
У нас тут нарисовался корень из нуля, сам не равный нулю. А ещё, от такого значения нельзя подсчитать корень. Нет такого значения матрицы, чтобы возвести в квадрат и получить его.
Видимо, чтобы при вычислении корня были получены любые значения, нужно предусмотреть добавление произвольной величины, которая этим способом не достигается. Соответственно, и вычисление квадрата теряет эту информацию. Как будто существования шести различных корней из единицы, без учёта сочетаний (
Расширение матрицы
Данный этап это так называемая «эйфория».Мы допускаем, что элементы матриц могут быть комплексным. Это расширяет представление и влияет не только на то, что мнимая единица может быть обозначена кроме
При
Другие составляющие при раскрытии скобок пропадают, потому что являются суммой произведений матриц в двух возможных направлениях:
А для всех трёх пар противоположные порядки произведения приводят к одинаковым результатам с противоположным знаком. То есть, в сумме дают ноль.
Если все элементы матриц поделить на
Справа посередине как раз матричное представление мнимой единицы через действительные значения элементов. А вместе с остальными двумя матрицами справа и простой единицей образует базу кватернионов. Это — числа подобные комплексным, но в которых используются уже две мнимые единицы, которые при различном порядке произведения образуют плюс или минус третью мнимую единицу, которая от них ничем, кроме порядка в тройке, не отличается.
Раскрытие комплексного числа через матрицу показывает, что порядок матрицы — количество строк и колонок — удваивается, и для одного шага перевода нужно выбрать, в какой тип представления превратить мнимую составляющую. И есть два отдельных варианта: сохранять комплексное значение на диагональных элементах, или выбрать для мнимой части значение из целой сферы значений. При этом, мнимые составляющие пропадают только у одной пары значений — из всей сферы. То есть, базис разложения в сферу в двух из трёх составляющих сохраняет мнимость элементов, то есть, для следующего уровня разбиения предлагает опять два варианта представления, причём, второй вариант опять сфера. И количество разбиений не ограничено.
Таблица умножения для матриц, строка на колонку:
Вот это поворот.
Оказывается, матричное представление с мнимой единицей на диагонали — тоже часть сферы. У него тоже есть значения матриц, которые соответствуют другим мнимым единицам кватерниона. Да, наверное, и всей мнимой гиперсферы, если расширять матрицу сразу с мнимой единицей на диагонали.
Произведение двух величин из различных мнимых гиперсфер будет давать значение из гиперсферы матриц паули — уже упомянутых корней из единицы, не совпадающих с самой единицей. Две мнимые гиперсферы образовались от выбора представления мнимой единицы не совпадающей с i на диагонали — на всех шагах расширения, и отражения этого решения на базис, включающий исключительно диагональное расположение. Но различное представление можно выбирать на каждом шаге расширения и даже отдельно для каждого мнимого элемента. Разнообразие результатов у произведения значений при этом заметно вырастает. Дополнительно можно рассмотреть и использование расширения единиц на матрицы паули. Ещё можно рассмотреть использование других простых чисел для коэффициента расширения матриц. Количество возможных значений тогда сильно возрастает.
Но до октонионов — значений с третьей базовой мнимой единицей
«Лучше всего, конечно, пять звёздочек»
Ну а самое лучше это использовать морфина гидрохлорид, пятипроцентный раствор.Для матриц второго порядка даже при использовании только действительных значений элементов к комплексному числу
Матрицы представляют собой схемы пересчёта одних векторов в другие, а добавочные значения (делители нуля и получисла) имеют признаки схлапывания — применённые в чистом виде они забирают возможность точного восстановления. Соответственно, для того чтобы обратить этот процесс, стоило бы придумать такие структуры, которые сохраняют значение, и при обратной операции его восстанавливают.
Как восстанавливаются значения, если они не потеряны? У матрицы второго порядка есть такая закономерность:
Величина
Одна перестановка столбцов или строк матрицы переключает знак у определителя — точно так же как знак результата меняется от изменения порядка произведения мнимых единиц.
Такими перестановками можно расставить по диагонали бóльшие элементы, оставив меньшие элементы вне диагонали — сравнение останется в рамках строки и колонки. И тогда матрицу как действие можно поделить — на скомпенсированную этими перемещениями часть, которая говорит о перестановке элементов вектора, и на остальное влияние значений друг на друга, которое является уже не обобщённым разворотом в пространстве, а некоторым обобщённым искажением.
Расчёт определителя основан на том, что если в матрице на всю колонку будет только одна единица, то результат будет равен, с точностью до знака, определителю матрицы без этой строчки и колонки. И если единицу «размазать» по колонке, то части определителя складываются линейно. Для объяснения вычисления вполне достаточно.
Для матрицы порядка два определитель это разница произведений элементов обеих диагоналей. Если элемент матрицы кватернион, то определитель считается всё же по действительному представлению матрицы, но при ненулевом определителе и тут возможно найти обратную матрицу.
Это будет задача со звёздочкой.
Полезно вспомнить, что изменение порядка в произведении обратных друг другу матриц не меняет результат. И что значения
Основание
Дело в том, что — видите.В нулевой степени любая величина станет единицей, а в единичной степени будет собой. Промежуточные степени возможны, но на комплексной плоскости они расположены на спирали, именно поэтому промежуточная степень
Для показательной функции
Особенности логарифма
То оно, например, видно сразу, чем отличается от чего.Производная от степенной функции будет произведением показателя и переменной в степени на единицу меньшей. Если подсчитать первообразную обратно, то получится, что нужно делить на величину
Производная логарифма игнорирует любой постоянный коэффициент у аргумента:
Циклическая неопределённость мнимой части логарифма остаётся, так как интеграл перед тем как из начальной точки дойти до конечной может покружить любое количество раз в любую сторону вокруг ноля, особенно если
Две параметризации
[Что одно — что другое, разница не имеет принципиального значения] — это можете вырезать полностью.Рассмотрим различие порядков операции на примере произведения кватернионов. Вот как выглядит произведение двух кватернионов в таком базисе, в котором у обоих нет третьей составляющей векторной части:
Произведению можно добавить такой параметр, который будет характеризовать порядок: при параметре 1 порядок совпадает с исходным, при параметре (-1) порядок обратный, при нулевом параметре различие уменьшается до нуля. Это можно сделать через коэффициент у перпендикулярной к общей плоскости обоих векторов составляющей.
В таком параметре есть два направления, плюс и минус. Всего два? По теореме Эскобара стоит добавить ещё направлений. Новое направление это будет средним между известными двумя: направлением первого вектора и направлением обращённого по знаку второго вектора. Тогда векторную часть результата произведения можно будет перенаправить двойным параметром по любому направлению на плоскости, на выбор. Обращение одного из векторов перед расчётом дополнительного направления здесь понадобилось для того чтобы при обмене векторов менялся и знак результата.
Параметр можно дополнить и третьим базисным направлением, рассчитанным просто как среднее между направлениями исходных векторов — оно будет перпендикулярно первым двум базисным направлениям. Но плавный обмен направлений исходных векторов не поменяет знак такого среднего направления. Поэтому результат определён только с точностью до знака, у одной составляющей выделенного базиса знак будет неопределён. Такие неопределённые значения — это уже не кватернионы, даже парой кватернионов они будут только до следующего произведения с такой же математической структурой с другим направлением неопределённости.
Различие порядка операции возведения в степень похоже на различие порядка при умножении кватернионов. «Гипотезой Эскобара» — я называю предположение о том, что возведение в степень можно параметризовать, примерно так же как выше умножение кватернионов.
У возведения в степень при одинаковом основании и показателе
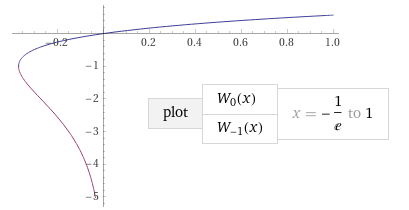
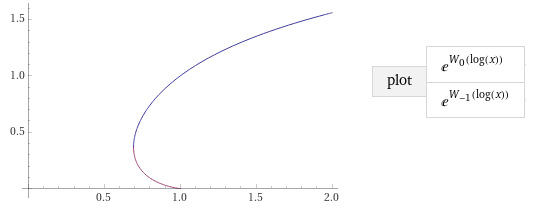
Интересно, как работают такие фокусы при использовании комплексных значений?
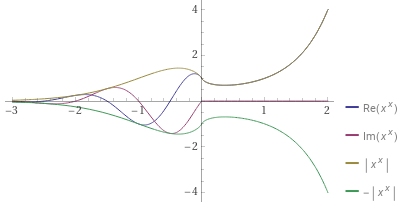
Если эту морковку развернуть, то ботва совпадёт с предыдущим графиком.
Если основание и показатель различаются, то зная их соотношение всё равно можно восстановить значения по результату, практически тем же самым способом.
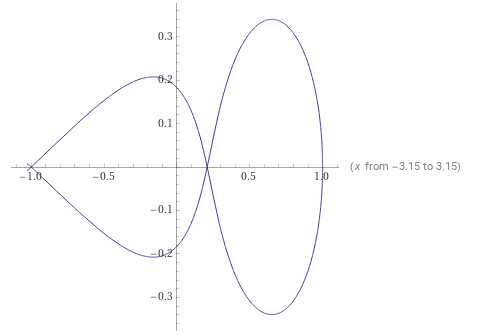
Видно, что в точке
В точке (-1) сам аргумент
Число
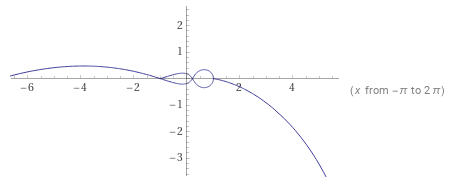

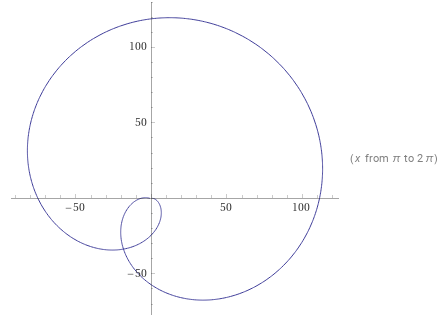
На каждом цикле абсолютное значение то становится меньше единицы, то становится больше единицы, и в логарифмическом выражении амплитуда раскачки растёт.

Если функцию
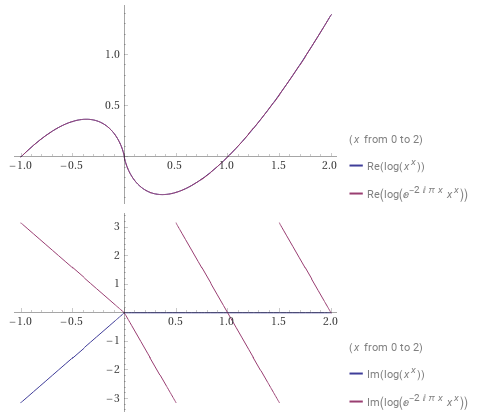
Мнимая часть логарифма даёт аргумент комплексного числа, то есть, фазу поворота. На графике сравнение двух вариантов: без сдвига фазы и со сдвигом на минус один оборот.
Для действительных значений
Для изображения графика пришлось выбрать, отрицательные значения — это поворот в комплексном пространстве по часовой или против часовой. При другом выборе фаза без сдвига при отрицательном аргументе направлялась бы не вниз, а вверх, а для отображения симметричного графика вниз надо было бы добавлять оборот, а не убавлять.
Теперь можно вспомнить о том что экспонента имеет и собственный целый произвольный аргумент.

Для того чтобы разобраться в топологии можно посмотреть на график функций

То есть, оборот функции
Значения функции

При нулевом
График при вращении

Точно такая же связность значений есть у функции квадратного корня — возвращение к прежнему значению за два оборота аргумента. Только, там оборот происходит вокруг нуля, а здесь вокруг ненулевого значения. И ещё отличие: в мнимой части различные витки различаются абсолютной величиной значения, а не только своим знаком.
Что особенного в значении аргумента
Можно сравнить графики.
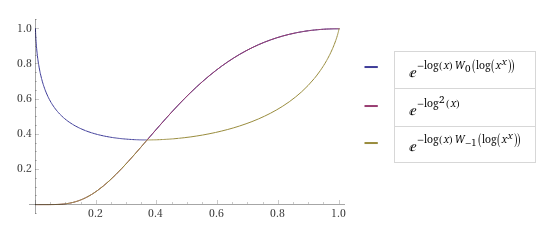
А вторая,
При аргументе
При параметрах 0 и (-1) функция ламберта при этом аргументе равна (-1). При других параметрах она принимает уже другое значение:
Ещё можно заметить, что при использовании параметра 1 знаменитое тождество Эйлера принимает вид:
Если обороты теряются:
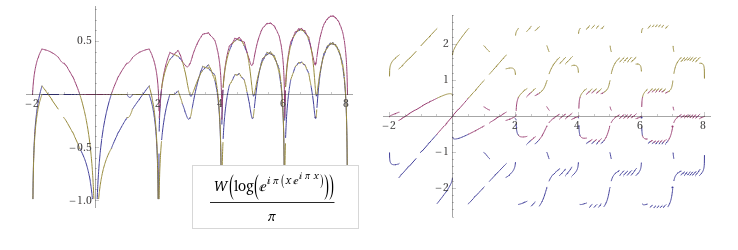
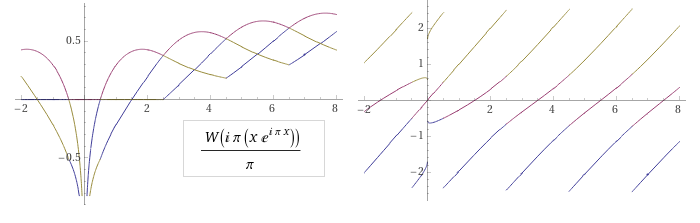
Второй вывод: для функции ламберта число
Что напоминает о возможности восстановить величину, находящуюся и в основании и в показателе степени, до нуля.
Итог: всё это, конечно, интересно, но вторую параметризацию сразу провести не удалось. Думаю, дело в том что операция возведения в степень не только некоммутативна, но и неассоциативна, наподобие произведения октонионов. Но это не значит, что вторая параметризация невозможна.
Коммутативность и ассоциативность
Не, я ещё пару слов.Сколь видов операции произведения существует, если её надо провести над двумя числами и она не коммутативна? Два, по различному порядку. Если одно из них уже было произведением, то получатся варианты:
Достаточно странно: казалось бы,
Идея о вставке возникает оттого что мнимая единица
Вставить множитель не только слева или справа, но и в середину можно было и раньше, от этого при использовании различных мнимых единиц кватерниона поменялся бы только знак. Можно было бы сначала умножить с любой стороны и поменять знак, получилось бы то же самое что и вставка в середину. А при отсутствии ассоциативности нужно дополнительно выбирать, какое из двух произведений со средним множителем происходит раньше.
Если до этого произведение велось над числами, и только потом происходило умножение на размерность, то теперь может быть не только два этих варианта — что размерность ставится справа, или размерность ставится слева, а потом переставляется вправо, изменяя числовую величину. Дополнительно можно предположить, что предыдущее произведение велось над числами, но с условием, что размерность уже присутствует, только будет добавлена позже. Тогда надо выбрать, у какой величины была эта размерность.
Такая размерность похожа на базис, только не отделяется до операции, чтобы вернуться после, а участвует в расчётах.
Дзета-функция
Что вот это вот, вот это, я вообще [не могу понять], что это [открывающая фигурная скобка] такое [закрывающая фигурная скобка]?
Если сравнивать суммы
«А потом дискотека»
Тири-ри-ри-ри ри-риПри приближении
Если взять
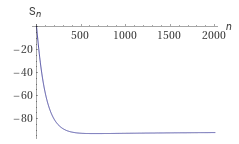
Видно, что сума сначала уменьшается, затем возрастает и, видимо, может и больше нуля стать.
Место смены направления можно найти, так как здесь различие больше всего приближено к нулю. Если решить
Если попробовать узнать где находится эта точка смены знака у различия, то на графике:

Будет видно, что при значении
Точка смены направления изменений существует при любом положительном отклонении
Например, на шаге
В статье «Удивительная и загадочная ????» показано, что существует способ уменьшить влияние той части суммирования, которая при существовании мнимой части
Полученное выражение сходится к тому же значению.

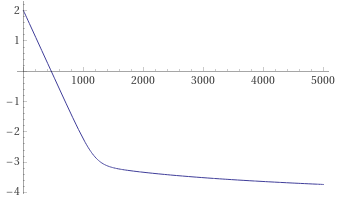
Правда, для
Комментарии (18)

sunnybear
21.11.2022 22:18+4И?

yurixi Автор
21.11.2022 22:38+2Пойти что ли музыкой заняться.

Refridgerator
24.11.2022 06:33А я наоборот, из музыки пришёл в математику) Захотелось большего разнообразия в звучании синтезаторов.

Sergeant101
22.11.2022 14:10+1Ну вы, сударь, будто самородок и не учились в университетах никогда - оси же подписывать надо, это вам любой преподаватель скажет.
Тяжело же в угадайку играть как у вас комплексная плоскость повернута, по-старому или по-новому.
Была и у меня когда то тяга к математике, жаль что это только для богатых.

Browning
22.11.2022 15:48+1Чтобы не выглядело как окрошка и маргинальщина, я бы сократил эксцентричное введение, добавил вместо него аннотацию или оглавление и добавил бы ссылки на внешние источники, в которых обсуждаются все эти вопросы, хоть бы и на Википедию. Скажем, римановы поверхности тут будут явно к месту. Так-то матричное представление комплексных чисел, от которого приходим к кватернионам -- это вообще-то симпатично и интересно, спасибо за эту часть.

yurixi Автор
22.11.2022 17:18Фрагмент про матрицы взят из другой статьи, которая была скрыта модераторами. Всё остальное — это переоформление этого фрагмента в новую статью, со своей темой. Похоже, не очень аккуратно получилось.

AllKnowerHou
24.11.2022 02:24Я конечно троечник в математике, но из вашей статьи следует что при увеличении размерности - увеличиваются количество мнимых единиц? То есть при n=1 i^2=-1 при n=2 их уже две, при n=3 их 4, при n=4 кватернионы их 8? Может я считаю неправильно, в предыдущем предложении надо начинать с n=2 и мнимых единиц одна и т. д. Но вот ваша статья кстати - я её бегло просмотрел наверное единственная где про кватернионы написано как бы вскользь, но не глупо. Я конечно понимаю что особо нигде не учат с ними работать и возможно считают хренью, но я вот знаю лишь одно практическое применение их - в играх, когда надо чтобы при беге рядом с npc они не траили(поддергивались) во время отрисовки. А тем более октанионы. Я бы даже посоветовал вам отправить вашу статью кому-нибудь преподавателю по высшей математике в университет. Единственно что даже меня болвана смутило - это функция W. И какие вы выводы сделали в итоге. Но меня зацепило то что при умножении матриц возможен двойной поворот и потеря знака - близнец числа I таким образом может потеряться как минус при расчётах. Но все-таки комплексные числа это же вектора - их можно графически нарисовать - нету этого у вас. Ещё мне понравились ваши графики с несимметричными функциями. Но суть вашей статьи я так и не уловил и логический ход мысли тоже, скорее всего из-за того что я троечник.

Refridgerator
24.11.2022 06:23А вы рассматривали функцию полилогарифма применительно к этой задаче?
Проблему с делением на ноль можно решить через дробно-рациональные числа. Это как обычные рациональные, но без ограничения на «только целые значения». Они позволяют дополнительно ввести множество нулей (0/1,0/2,0/pi,...), множество бесконечностей (1/0,2/0,pi/0,...) и оперировать ими без потери информации. Правда, для это потребуется явно определить все операции и функции. Например, можно определить сложение как [a,x] + [b,z] -> [(a·z+b·x)/(x+z),(x·z)/(x+z)], и тогда при наличии только одного нуля в знаменателе мы будем получать алгебраически корректный результат (а если в обоих — уже нет).


Tzimie
Эээ...Ммм... Многа букафф. Многа формул. И чувство какой то окрошки.
yurixi Автор
Это вопрос «плавного обмена» аргументов возведения в степень. Рассматривается последовательно и без особых результатов. Сначала речь про комплексные числа, у них можно произведение сделать с плавным обменом. Затем рассматривается функция ламберта, чем она может помочь. Результат таков, что вопрос слишком сложный. Если б решение было, можно было бы выстроить не окрошечно.
novoselov
Еще с университета узнал что шизофрения среди математиков довольно распростроненное явление, один преподаватель у нас купировал приступы алкоголем, другой просто тихо сходил с ума в своей гениальности.
domix32
И при всем притом как-то мало информации про того Эскобара во всей этой истории
yurixi Автор
Это устаревающий мем, его наоборот может быть слишком много если начать вдаваться в детали.
А если речь про «того» Эскобара, то там уже куда фантазия заведёт — факты с других витков времени не сохранились.
DarthPadla
domix32
У этого аксиома, а не гипотеза
Refridgerator
Вы, похоже, статьи других математиков не читали) У автора как-раз таки всё кристально прозрачно, логика прослеживается и обосновывается. Понятно, что раз статья не научпоп — вникать в смысл, в том числе и формул, таки надо.