Каждый день каждый человек своими глазами видит как всё вокруг происходит. От этого выработалась не только знание как всё будет дальше, но и её подтверждённая часть — интуиция. Но у такой интуиции, которая по происхождению основана на прошлом есть один явный недостаток — она основана именно на прошлом опыте, к новым открытиям она не готова. Это явно выражается, например, в том с каким отношением к квантовой механике рассказывали те кто её открывал. «Мы творим лютую дичь» — говорили они. А что такого в том чтобы так говорить? Несоответствие интуиции есть, и никто пока до конца не разобрался. Студенты: «Так и запишем, «Мы творим лютую дичь. И разбираться не нужно»» (фейспалм). И до сих пор иногда это проскакивает в виде слова «заткнись» в описаниях — во вполне академических. И исчезать не торопится. Что ж, не все прежде чем делать открытия учились тому как надо делать открытия. Но если придумать новую интуицию, всё было бы гораздо, гораздо симпатичней.

«Чёткость» и «Плавность» — два раздела статьи.
Начну с абстрактной задачи.
Представьте, что сотрудников вашего института вывели на улицу и построили в линейку. И раздали всем наборы конфет. Скажем, в наборе круглое число, 1024 конфеты, делить пополам можно аж десять раз. Но количество наборов меньше, чем количество человек и поэтому наборы достались не всем. Количество конфет очень важно на поляне чаепития, поэтому вы даёте команду: каждому, половину того что есть — отдать соседу слева. Распределение немного размылось.
И вот такой интересный вопрос: можно ли сформировать такую следующую команду по раздаче, чтобы обратить предыдущую команду, то есть, чтобы наоборот, собрать? Можно ли достичь чёткости через «размытие»? Оказывается, можно. Только, придется величину раздачи допустить отрицательной и оперировать на любом расстоянии, а не только обмениваться с соседями.
Влево надо раздавать чередуя минус и плюс. Себе оставить долю. И вправо чередуя плюс и минус. Например, если всего пять человек, то схема обмена будет такой:
Проследим за процессом. Сначала набор был только у третьего, после первого обмена конфеты есть у второго и третьего. Следующий обмен рассчитывается суммированием единиц со знаком, взятым из таблицы, умножив строчку на количество конфет у соответствующего сотрудника. То есть, используется только вторая и третья строка и останется просуммировать по колонкам. Все колонки кроме третьей суммируются в ноль — весь набор конфет собирается обратно, третьему. Все отрицательные раздачи лишние, и компенсируются лишними положительными. Алгоритм работает.
Тут есть пара проблемок. Первая: непонятно, кому же отдаст половину самый левый. Но это решить просто, надо изначально левому не давать конфет. Хех. Ну, или пусть отнесёт самому правому, то есть, линейку можно зациклить.
А вторая проблемка: алгоритм хорошо работает для нечётного количества человек, а если число чётное, то уже нет. Ну, представьте что у вас всего два человека, после первого распределения у них всегда оказывается количество одинаковое, и какая часть от кого перешла — никак не восстановить.
И, например, для четырёх человек можно заметить, что распределение плюсов и минусов при зацикливании начинает противоречить само себе: знаки при наложении соседних циклов противоположны. Так что, остаётся только использовать алгоритм для пяти, но пятый участник будет отсутствовать: то есть, ни раздавать конфеты, ни получать.
Надеюсь, бесконечность не является чётной? А то, в этом случае обобщить на линейку с бесконечным количеством элементов может и не получиться. Думаю, надо обязательно, чтобы этот сотрудник, попавший на линейку на бесконечное место, гарантированно не участвовал в обмене. И все его соседи тоже. А может, бесконечность тем и отличается, что можно рассчитывать на тот вариант, который получше? Тогда — пожалуйста, пусть она будет нечётная. Тогда в обмене будут участвовать все.
Это важный момент — один лишний отсчёт и точное восстановление в общем виде не работает, появляюся варианты.
(* Вставить иллюстрацию, промт: одинокий сотрудник стоит на «бесконечном месте», никаких конфет, темно.)
При переходе с шутливых аналогий на математическое описание надо рассказать о понятии свёртка. Это именно то что происходило при команде поделиться конфетами. Сама операция свёртки — это операция над двумя функциями, которая даёт третью, в которой каждое из значений первой линейно перераспределено по схеме из второй.
Например, эхо. Это же свёртка функции того что вы крикнули и схемы повторения. Или, например, если в небе происходит солнечное затмение, то тень становится покрытой множеством маленьких солнечных месяцев. Результат здесь — это свёртка того что видно в небе и схемы расположения отверстий в преграде для света.

Математически это выражается так:
Или можно применить нечто среднее:
Самое характерное свойство у свёртки это линейность, оно выражается в том что если взять две функции, каждую свернуть с третьей и потом результаты сложить, то это будет то же самое как если бы функции сначала были сложены, а потом была произведена свёртка. То есть, не важно когда складывать, до свёртки или после.
К этому моменту у нас кроме начального распределения есть пара функций: функция размытия и функция возвращения резкости. Свёртка со второй — обращает свёртку с первой.
Размывающее распределение «отдай соседу половину» можно повторять много раз. Раздачу лучше чередовать влево и вправо, тогда после каждой такой пары начальный элемент будет оставаться в центре распределения. Ситуацию можно рассмотреть только с одним установленным вначале элементом, остальные варианты получаются свёрткой. Посмотрим на формулу для расчёта значений, которые получаются сразу на выбранном шаге.
Если при каждом делении дополнительно умножать на два, тогда значение элемента будет просто суммой предыдущего значения элемента и предыдущего значения соседнего элемента, со стороны с которой передают. Тогда самый крайний элемент такого распределения будет оставаться единицей. А первый соседний элемент будет суммой таких единиц, выполненных столько раз, сколько прошло шагов. Значит, равно количеству шагов.
Следующий, второй соседний элемент, точно так же последовательно суммирует предыдущие суммы. И дополнительно нужно учесть, что в цепочке суммирования последнее слагаемое будет на единицу меньше, чем номер шага, поэтому формула второго элемента будет![$n(n-1)/2$]() , с минусом перед единицей.
, с минусом перед единицей.
Чтобы получить третий элемент нужно умножить второй на![$(n-2)/3$]() . Просматривается общая формула:
. Просматривается общая формула:
Теперь останется отменить умножение на два на каждом шаге — поделить на двойку в степени номера шага — и значение результата размытия будет получено. Расчёт в случае отсчёта позиции от крайнего элемента:
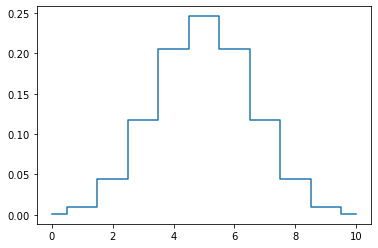
И вот тут такой вопрос — при увеличении шагов этот холмик расширяется или сужается? С одной стороны размытие это расширение в разные стороны. С другой стороны, взгляните график распределения распределения после 200 шагов.

Относительно всей области размытия холмик выглядит как узенький всплеск посередине, относительно всей широты фигура с каждым шагом только сужается.
Если на масштабе одного элемента распределение расширяется, а на масштабе всей области распределение сужается, то сохраняется фигура холмика с увеличением шагов только на среднем масштабе. Ориентировочные размеры — это корень из количества шагов. Или, наоборот, количество шагов соразмерно квадрату от количества делений для выбранной ширины.
При увеличении шагов до бесконечности на среднем масштабе распределение приближается к функции Гаусса. Вы встречали в фотошопе «размытие по Гауссу»? Это многократно повторяющееся размытие на один пиксел, которое приводит к замутнению картинки. Если не брать во внимание сдвиг от центра и всевозможные коэффициенты для аргумента и для значения, формула гауссианы будет такой:
Пусть у среднего элемента индекс![$n^2$]() . У крайнего элемента тогда будет индекс
. У крайнего элемента тогда будет индекс ![$2n^2$]() . Отслеживать масштаб будем по элементу
. Отслеживать масштаб будем по элементу ![$n$]() от центра, с индексом
от центра, с индексом ![$n^2+n$]() . Отношение его значения и значения среднего элемента при увеличении
. Отношение его значения и значения среднего элемента при увеличении ![$n$]() будет стремиться к некоторому числу, выразим его.
будет стремиться к некоторому числу, выразим его.
![$x$]() не нужно, отслеживаемая точка среднего масштаба
не нужно, отслеживаемая точка среднего масштаба ![$e^{-x^2}$]() расположена при
расположена при ![$x=1$]() .
.
Дальше считаем интеграл функции, чтобы нормировать до единицы, как у первоначального элемента. Производная от![$e^{-x^2}$]() равна
равна ![$-2xe^{-x^2}$]() , это позволяет проинтегрировать это выражение обратно.
, это позволяет проинтегрировать это выражение обратно.
Нормированная гауссиана
Теперь можно задаться вопросом, как в таком же пределе выглядит отрицательное количество шагов размытия.
Для того чтобы получить схему распределения для отмены двух шагов размытия нужно свернуть функцию для шага обращения размытия с ней же самой.

Диаграмма применения второго шага наведения резкости по принципу первой диаграммы (из плюсов и минусов), но уже с применённым изменением знака, в соответствии с множителем внутри свёртки. Светлым обозначен плюс, тёмным минус. Описать расстановку можно так: знак зависит от чётности места получателя, и у тех мест что ниже диагонали знак изменён на противоположный. Суммирование по колонкам приводит к распределению: одно из значений равно количеству элементов в линейке, и отдаляющиеся от неё в обе стороны — уменьшаются по абсолютной величине на два, и ещё меняют знак, сходясь до минус единиц на двух противоположных ему в цикле элементах.
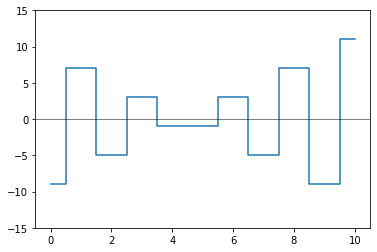
При дальнейшем наведении резкости знак в расстановке так и продолжит чередоваться. Эту постоянную смену знака можно исключить из внимания, оставив только положительные значения на каждом шаге. Меняем знак у колонок с нечётным индексом на противоположный. Тогда, на этом же примере, можно подсчитать, что суммы по колонкам будут от -9 до 11 с шагом 2. Но все числа распределения теперь же уже положительные, что делать с отрицательными? В получившуюся функцию отрицательные числа не попадают, потому что с каждым шагом схема чередования знака сдвигается — и для мест, где знак отрицательный он при этом меняется.
Если количество шагов размытия превысит количество элементов, то конечно, значения, разошедшиеся в разные стороны, снова сойдутся и произойдёт наложение. Для вычисления соответствующего наведения резкости это дополнительно усложнило бы распределение. Но восстанавливающие значения расстановки для этого случая всё равно существуют и работают.
На одиннадцати элементах третий шаг наведения резкости приводит к таким значениям:
При рассмотрении размытия был интересен масштаб для стабилизации холмика. Здесь же значения занимают всю линейку, какой бы она ни была, и уже на третьем шаге нет ни одного значения меньше, чем количество элементов. Никаких холмиков здесь не наблюдается. Тогда, какие же здесь закономерности? Ну, кроме уже принятого во внимание чередования знака.
Первый шаг наведения резкости выражается просто.![$n$]() будет означать место максимума.
будет означать место максимума.
![$k=11$]() значение
значение ![$R^{[2]}_{11}=\{1,3,5,7,9,11,9,7,5,3,1\}$]() . Сумма в общем виде получилась равной
. Сумма в общем виде получилась равной ![$\frac{k^2+1}{2}$]() .
.
На третьем шаге форма распределения парабола.![$R^{[3]}_{11}=\{11,29,43,53,59,61,59,53,43,29,11\}$]() . Сумма в общем виде
. Сумма в общем виде ![$\frac{k^3+2k}{3}$]() .
.
Для перехода на следующий шаг нужно из выражения для предыдущего уровня вывести выражение суммы диапазона элементов. Так как зависимость значений от![$n$]() это зависимость от
это зависимость от ![$|n|$]() , то сумму можно подсчитать только в одну сторону на половину всех элементов, умножить на два, и от суммы отнять максимум прошлого уровня, потому что он попал туда два раза.
, то сумму можно подсчитать только в одну сторону на половину всех элементов, умножить на два, и от суммы отнять максимум прошлого уровня, потому что он попал туда два раза.
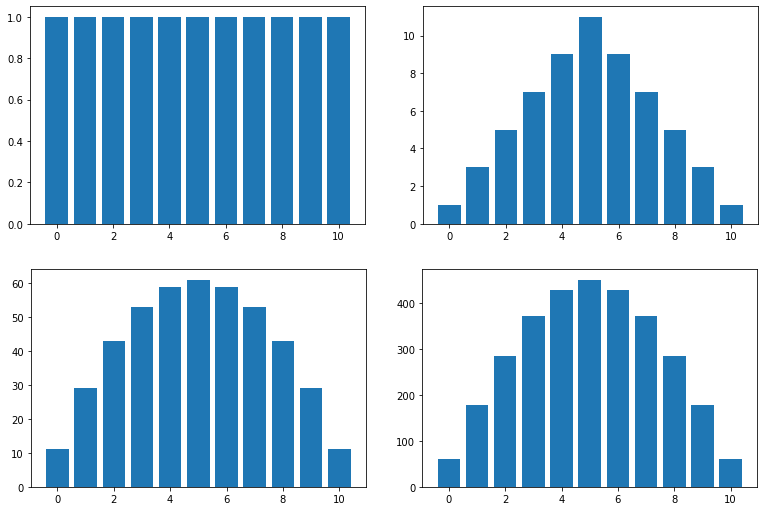
Пятый шаг:![$v$]() до предела
до предела ![$\frac{k-1}{2}-|n|$]() , и перевод
, и перевод ![$n$]() в
в ![$v$]() . В верхнем пределе расчёта суммы есть разворот
. В верхнем пределе расчёта суммы есть разворот ![$(\text{константа})-n$]() , то есть, верхний предел суммы и переменная различаются. И это для меня похоже на дополнительное усложнение. Поэтому стоит попробовать рассмотреть расстановку в другой системе отсчёта — от другого из двух «центров» замкнутой линейки.
, то есть, верхний предел суммы и переменная различаются. И это для меня похоже на дополнительное усложнение. Поэтому стоит попробовать рассмотреть расстановку в другой системе отсчёта — от другого из двух «центров» замкнутой линейки.
Переориентируем систему отсчёта так:

Ну что, пятый шаг выполнен, бесконечность — уже совсем близко.
Можно подумать, что график распределения это косинус, но он может совпадать с ним только в пределе. При ограниченном количестве шагов всегда есть очень важное, даже принципиальное отличие.
Получилась вот такая общая формула:
![$n$]() . А теперь это всё хотелось бы выразить через
. А теперь это всё хотелось бы выразить через ![$x$]() .
.
Этого для поверхностного представления того как выглядит изнанка размытия хватит.
Наведение резкости можно назвать отрицательной степенью размытия. Если подставить в формулу![$g_k(x,k)=\sqrt{\frac{k}{\pi}}e^{-{x^2k}}$]() отрицательное число для степени размытия, то возникнет чисто мнимая функция с неопределённым знаком, которая в обе стороны только возрастает. Для мнимого значения этой функции в дискретном распределении явно просматривается соответствие с чередованием знака. Попробуем разобраться с остальным.
отрицательное число для степени размытия, то возникнет чисто мнимая функция с неопределённым знаком, которая в обе стороны только возрастает. Для мнимого значения этой функции в дискретном распределении явно просматривается соответствие с чередованием знака. Попробуем разобраться с остальным.
Между размытием и резкостью есть ещё одно общее свойство — постоянное значение они оба переводят в постоянное значение. Но если для размытия это выглядит как суммирование соседних значений и затем деление на два — что для одинаковых значений возвращает к нему же — то для резкости расчёт происходит немного по-другому.
Если мы знаем, что элемент чёткой линейки равен![$a$]() , при том что у соответствующей размытой линейки всё заполнение константа
, при том что у соответствующей размытой линейки всё заполнение константа ![$c$]() , то мы можем сказать, что соседние элементы для
, то мы можем сказать, что соседние элементы для ![$a$]() это
это ![$c-a$]() , ведь в сумме должны давать
, ведь в сумме должны давать ![$c$]() . Это, в случае если мы при размытии не делим на два. Если делим, то
. Это, в случае если мы при размытии не делим на два. Если делим, то ![$2c-a$]() . Следующие соседние элементы должны быть опять значением
. Следующие соседние элементы должны быть опять значением ![$a=2c-(2c-a)$]() . Такой расчёт происходит до тех пор пока оба потока расчёта соседей не встречаются на противоположной стороне замкнутой линейки. А там происходит такое наложение, что для равенства значений должно выполняться
. Такой расчёт происходит до тех пор пока оба потока расчёта соседей не встречаются на противоположной стороне замкнутой линейки. А там происходит такое наложение, что для равенства значений должно выполняться ![$a=2c-a$]() . Значит,
. Значит, ![$a=c$]() .
.
У линейки можно отделить общее постоянное значение, чтобы его пересчитывать на следующий шаг просто добавлением, не проводя через расчёты. При таком отделении от линейки размером![$k$]() только с одним установленным элементом
только с одним установленным элементом ![$a$]() все значения уменьшатся на
все значения уменьшатся на ![$a/k$]() . У самого элемента значение станет
. У самого элемента значение станет ![$a\left(1-\frac{1}{k}\right)$]() .
.
С постоянным значением всё просто. Но кроме постоянного значения есть и другие формы распределения, которые при размытии не меняют формы.
Что будет если вы сложите две синусоиды, которые не отличаются ни амплитудой, ни частотой, а только фазой? Если фазы будут не противофазами друг другу, то результат тоже будет синусоидой, с той же частотой. Поэтому, если распределение будет гармонической функцией по частоте кратной размеру линейки, то и при размытии и при резкости она останется гармонической функцией той же частоты, поменяв только амплитуду.
В полном соответствии со школьной формулой![$\small\cos(a)+\cos(b)=2\cos\left(\frac{a+b}{2}\right)\cos\left(\frac{a-b}{2}\right)$]() размытие выглядит так:
размытие выглядит так:
![$w$]() — частота или кратность превышения размера линейки над длиной волны, целое значение расположено в диапазоне от
— частота или кратность превышения размера линейки над длиной волны, целое значение расположено в диапазоне от ![$0$]() до
до ![$(k-1)/2$]() . Если ставить больше, то правый множитель в правой части переключит свой знак.
. Если ставить больше, то правый множитель в правой части переключит свой знак.
Думаю, сильно заметно, что после пары одинаковых шагов размытия центр на один отсчёт уплывает, постоянно приходится следить куда уплыл. Пора вводить третью координату, которая остаётся нулём в месте центра размытия.
Новая координата такая:![$x+n=k/2$]() ? В равенстве
? В равенстве ![$x+n=k/2$]() координаты
координаты ![$x$]() и
и ![$n$]() определены на одном и том же шаге размытия, чтобы
определены на одном и том же шаге размытия, чтобы ![$x+1/2$]() и
и ![$n$]() были целыми. А здесь шаги разные. Положение центра размытия с каждым шагом чередует привязку к отсчётам расстановки: оно то попадает на элемент линейки, то находится между двумя элементами. Поэтому положение центра будет чередовать эту привязку. Для нового равенства не только
были целыми. А здесь шаги разные. Положение центра размытия с каждым шагом чередует привязку к отсчётам расстановки: оно то попадает на элемент линейки, то находится между двумя элементами. Поэтому положение центра будет чередовать эту привязку. Для нового равенства не только ![$n$]() , но и
, но и ![$x$]() будет целым. И ещё у
будет целым. И ещё у ![$n$]() исправлено направления возрастания, чтоб совпадало с
исправлено направления возрастания, чтоб совпадало с ![$a$]() .
.
Перепишем предыдущую формулу для новой координаты. Теперь операции над гармонической функцией записываются однообразно. Для размытия нужно умножить, а для резкости, соответственно, поделить:![$a$]() не всегда соответствует целому номеру элемента, теперь можно отделять не только постоянную составляющую, но и все кратные колебательные составляющие, и преобразовывать их раздельно, а потом складывать.
не всегда соответствует целому номеру элемента, теперь можно отделять не только постоянную составляющую, но и все кратные колебательные составляющие, и преобразовывать их раздельно, а потом складывать.
Тут может заинтересовать функция, которая остаётся после отделения всех гармонических составляющих.![$k$]() отсчётов переходит в коэффициенты, количеством два по
отсчётов переходит в коэффициенты, количеством два по ![$((k-1)/2+1)$]() , это
, это ![$k+1$]() . Здесь на один можно убавить, так как фаза для постоянной компоненты не используется. Тогда при разложении на коэффициенты пространство вариантов совпадает по размерности, поэтому остатка может и не быть.
. Здесь на один можно убавить, так как фаза для постоянной компоненты не используется. Тогда при разложении на коэффициенты пространство вариантов совпадает по размерности, поэтому остатка может и не быть.
Как отделять частотные составляющие? Чтобы рассчитать одну из них нужно просуммировать функцию, умножив на косинус заданной частоты и отдельно просуммировать, умножив на синус заданной частоты.
Собрать из косинусов можно любой отдельный отсчёт, нужно лишь чтобы сдвиг фазы у всех косинусов помещал гребень на него. А это значит, что любое распределение полностью раскладывается на гармонические функции, без остатка.
Используя такое разложение на косинусы, вместе с полученным выше расчётом для косинуса одного шага размытия, можно вывести выражение для расчёта расстановок для любого количества шагов размытия одного элемента.![$L$]() может быть отрицательным, определяя расстановку для наведённой резкости.
может быть отрицательным, определяя расстановку для наведённой резкости.
Какая симпатичная формула получилась, простая и ясная, мне нравится. Теперь для распределения имеется три формулы: для размытия, для резкости и общая, которая позволяет расчитать результаты для обеих.
У этого варианта есть одно дополнительное свойство. Похоже, расстановку можно так определять не только для целых, но и для действительных значений — как для позиции, так и для степени размытия.
Количество элементов![$k$]() можно не ограничивать, получится сумма значений бесконечности элементов. При таком суммировании есть свои особенности. В первую очередь, что все элементы могут быть околонулевыми, а их сумма будет отличаться от нуля, произвольно сильно. Поэтому между количеством элементов и их значением следует добавить коэффициент, который задаст сумме неограниченного количества элементов ограничение. Его суть — согласование двух разных масштабов.
можно не ограничивать, получится сумма значений бесконечности элементов. При таком суммировании есть свои особенности. В первую очередь, что все элементы могут быть околонулевыми, а их сумма будет отличаться от нуля, произвольно сильно. Поэтому между количеством элементов и их значением следует добавить коэффициент, который задаст сумме неограниченного количества элементов ограничение. Его суть — согласование двух разных масштабов.
Задаётся он через отношение суммы из таких околонулевых значений элементов, которые соответствуют единице, и количеством суммируемых элементов. Коэффициент стремится к нулю, но ему не равен. Множитель![$dx$]() в интеграле — это он и есть. Он переводит значение функции в значение элементов, чтобы интеграл как сумма элементов перевёл это в масштаб значения функции. Значение каждого элемента будет неотличимо от нуля, но при делении на коэффициент значение становится привычного порядка единицы.
в интеграле — это он и есть. Он переводит значение функции в значение элементов, чтобы интеграл как сумма элементов перевёл это в масштаб значения функции. Значение каждого элемента будет неотличимо от нуля, но при делении на коэффициент значение становится привычного порядка единицы.
Превратим общую формулу размытия в интеграл. Дробь![$1/k$]() , которая тут уже есть, становится
, которая тут уже есть, становится ![$dx$]() . Отношение
. Отношение ![$w/k$]() становится
становится ![$x$]() . Пределы тоже меняются соответственно, становясь плюс и минус одной второй. После этого можно не опасаться превышения количества шагов над количеством элементов, и частоты оказываются ограниченными — не по количеству, а по величине.
. Пределы тоже меняются соответственно, становясь плюс и минус одной второй. После этого можно не опасаться превышения количества шагов над количеством элементов, и частоты оказываются ограниченными — не по количеству, а по величине.
Я сразу решил посмотреть, как выглядит Гауссиана, выраженная как предел бесконечности шагов размытия с сохранением масштаба.
Как собирать распределение из гармонических функций для неограниченного числа элементов — ясно, а как его на эти гармонические функции разбирать?
Если начальный элемент будет не по нулевой координате, то его распределение будет содержать не только косинусы — фаза будет сдвинута, а значит, и синусы появятся. Значит, при разборе распределения нам опять понадобится отдельно выявлять косинусы и отдельно синусы. И после этого у нас получится целых два значения. Лучше это сразу объединить в одно.
Стоит использовать комплексные числа, и вместо двух функций результата иметь одну функцию, значение у которой содержит одно комплексное число, две составляющих, реальную и мнимую. Кроме того, сама гармоническая функция может быть выражена как косинус в реальной части и синус в мнимой.![$e^{2\pi iwx}=\cos(2\pi wx)+\sin(2\pi wx)i$]() . И тогда чтобы определить отдельные составляющие нужно подсчитать сумму или интеграл исходной функции, просто умножив на соответствующую этой составляющей двухкомпонентную гармоническую функцию.
. И тогда чтобы определить отдельные составляющие нужно подсчитать сумму или интеграл исходной функции, просто умножив на соответствующую этой составляющей двухкомпонентную гармоническую функцию.
Реальная часть разделяемой функции при умножении на реальную часть гармонической функции будет выделять косинус, а при умножении на мнимую часть гармонической функции будет выделять синус, и в результате число, которое получено, само определяет амплитуду и фазу, своим модулем и аргументом.
Кроме этого, мнимая часть разделяемой функции при умножении на мнимую часть гармонической функции будет образовывать отрицательный вклад в реальную часть результата, и при умножении мнимой на реальную в мнимой части результата тоже будет вычет. Но из-за того что детектируемые частоты разделяются на отрицательные и положительные, через то что у синуса в мнимой части различный знак, по итогу детектируется именно нужная частота, а противоположная, если её там нет, приводит к нулевому результату.
Для того чтобы определить составляющую нужно умножать на гармоническую функцию — но не той частоты, которая при этом определяется, а противоположной по знаку. Потому что произведение со значением с обратной частотой приводит к противодействию вращению в комплексном пространстве, и элементы суммы перестают кружить вокруг нуля, давая в результате суммирования не нулевое значение.
Сбор расстановки из гармоник:
Но интегралом разбор тоже может быть, потому что в «плавном представлении» каждый отсчёт свёрнут с функцией![$\operatorname{sinc}(x)=\{\sin(\pi x)/(\pi x),(1\Leftarrow (x=0))\}$]() , которая имеет нули при всех целых аргументах, кроме нулевого, и её интеграл равен единице. И, кроме того, будут присутствовать все частоты в рамках
, которая имеет нули при всех целых аргументах, кроме нулевого, и её интеграл равен единице. И, кроме того, будут присутствовать все частоты в рамках ![$[-1/2;1/2]$]() . Точнее, только они и будут.
. Точнее, только они и будут.
Здесь уже можно отметить: свёртка двух расстановок будет давать такую же раскладку как произведение соответствующих раскладок от этих двух функций. Например, размытие получается свёрткой заданной расстановки с расстановкой размытия, но при сборе из гармоник раскладка из косинусов, которая получилась бы без размытия, умножается на косинусы, которые сами являются раскладкой от размытия. Короче,![$\operatorname{sinc}()$]() , которая ограничена по частоте, то в частотном диапазоне функция тоже будет ограничена по частоте. И наоборот, такое ограничение по частотам это свёртка отдельных регулярных отсчётов с
, которая ограничена по частоте, то в частотном диапазоне функция тоже будет ограничена по частоте. И наоборот, такое ограничение по частотам это свёртка отдельных регулярных отсчётов с ![$\operatorname{sinc}()$]() .
.

Эти преобразования можно сделать однообразными, использовав вместо суммы интеграл и избавившись от коэффициента перед частотой в показателе в выражени для![$R$]() .
.
![$U$]() тоже уйдёт. Частотный диапазон у
тоже уйдёт. Частотный диапазон у ![$\operatorname{sinc}(x)$]() из-за такого перопределения станет
из-за такого перопределения станет ![$[-\pi;\pi]$]() .
.
После этого образовавшийся общий коэффициент перед интегралом можно раскидать между прямым и обратным преобразованием, будет:
Первая функция, которая испытает преобразования Фурье на себе, у нас будет, конечно же, гауссиана.
![$b=5$]() , соответствующее частотному представлению после 50 шагов размытия одного элемента, хорошо её приближает.
, соответствующее частотному представлению после 50 шагов размытия одного элемента, хорошо её приближает.
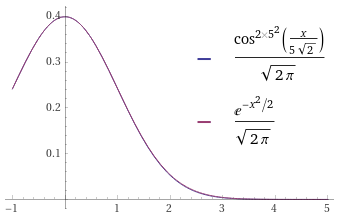
Если проследить за тем как постепенно с каждым шагом размытия косинус превращается в экспоненту, то можно увидеть, как от него удаляется второй гребень, и меняется при этом в знаке, соответственно степени от отрицательного числа.
 А третий гребень, удаляясь, знака не меняет.
А третий гребень, удаляясь, знака не меняет.
В общем, интересный получился предел.
![$1-x^2/2$]() .
.
Теперь, когда преобразование фурье выведено, мы займёмся дальнейшими экспериментами над гауссианой.
Эталонная гауссиана не меняется при преобразовании фурье, и её фурье-образ с ней совпадает.
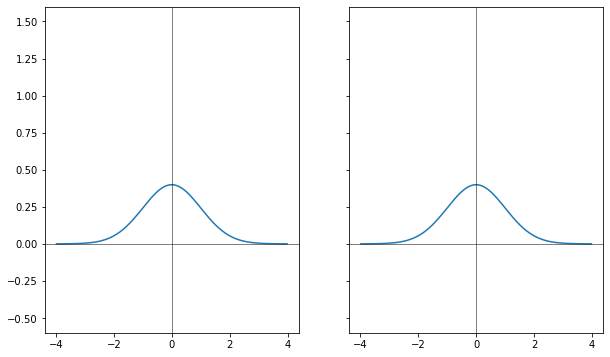
С общим множителем преобразование ничего не делает, оставляет каким был.
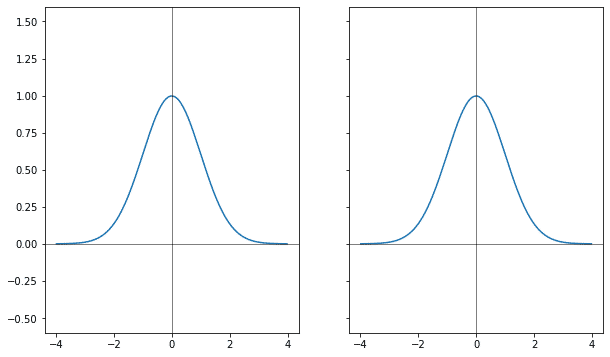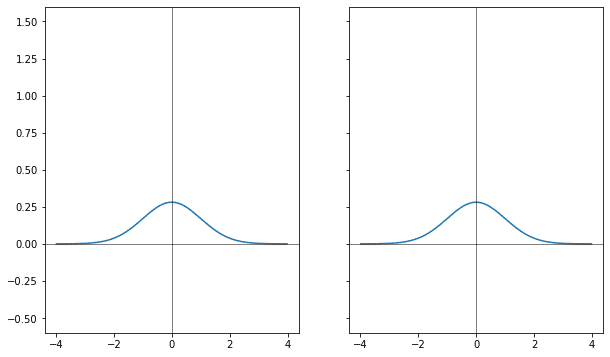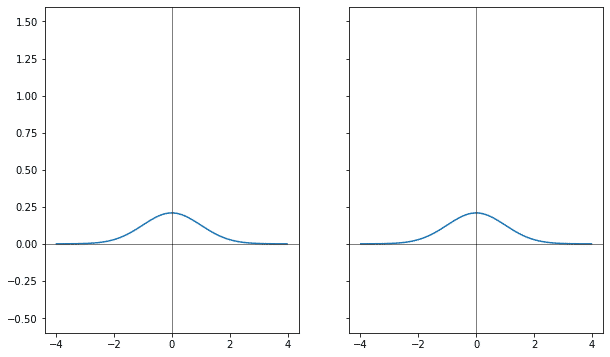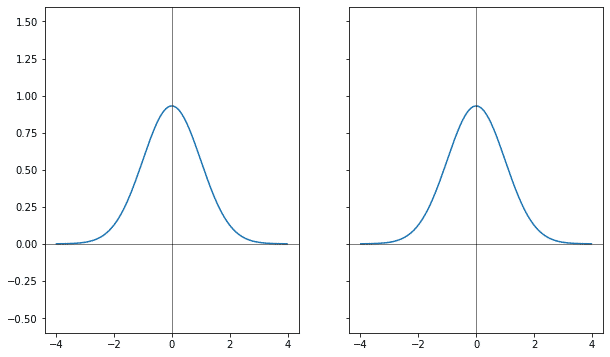
Если через коэффициент к аргументу у гауссианы менять ширину, расширять, то её фурье-образ меняется сразу в двух направлениях: он и сужается и растёт.
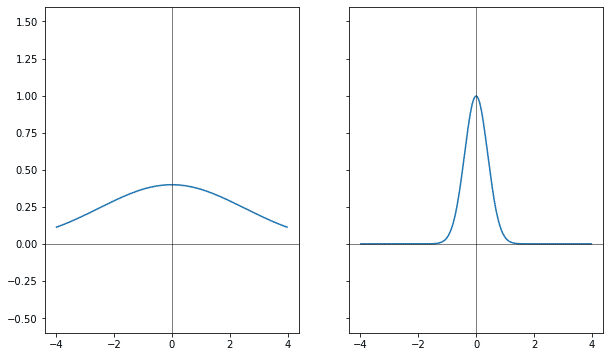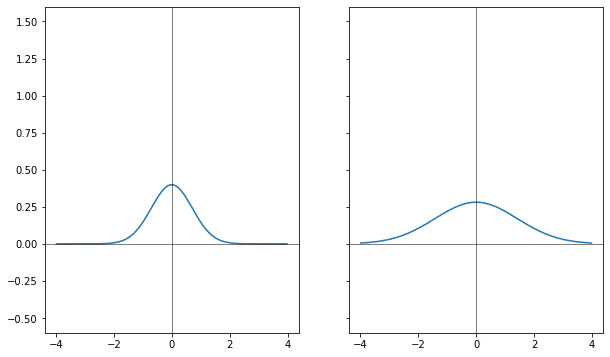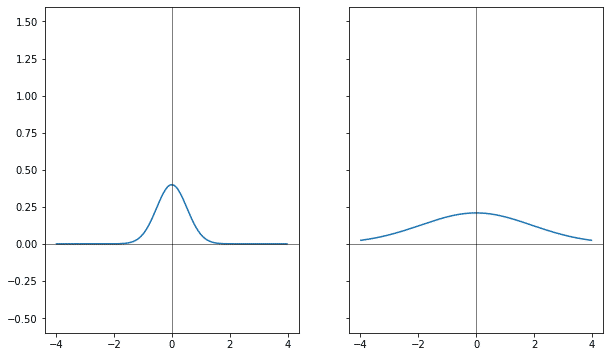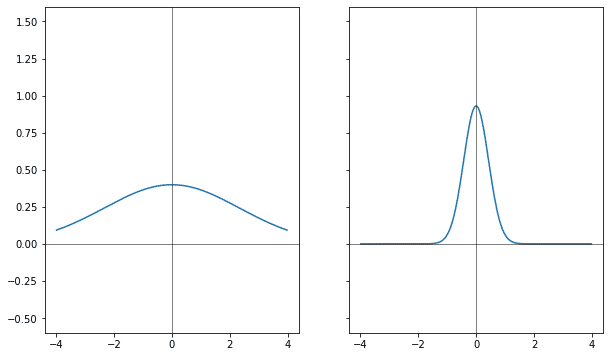
Используя линейность преобразования можно изменение высоты распределить между исходником и результатом преобразования, тогда получится, что когда одна из функций растёт, другая уменьшается.
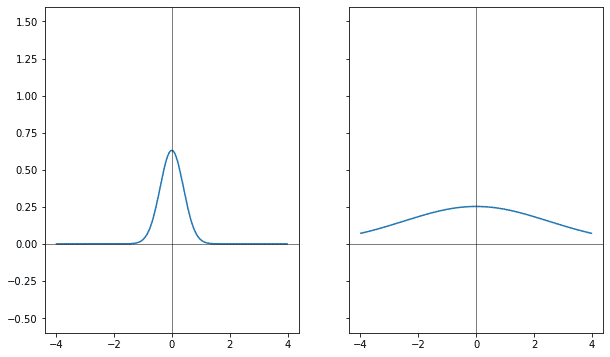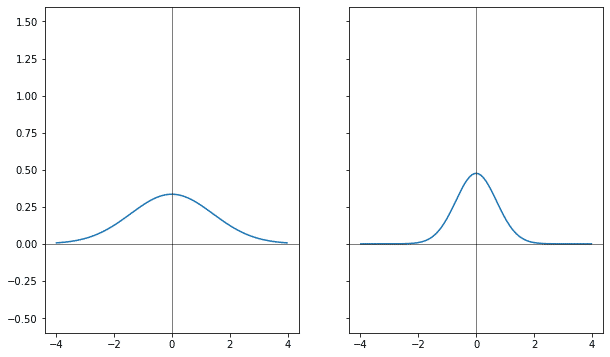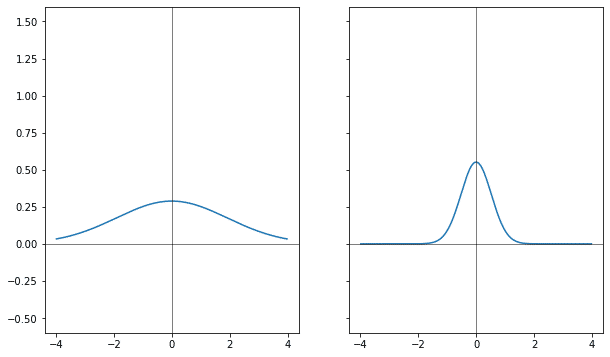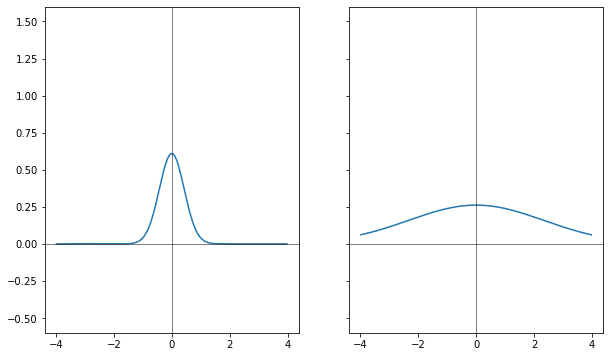
Следующий эксперимент — со сдвигом.
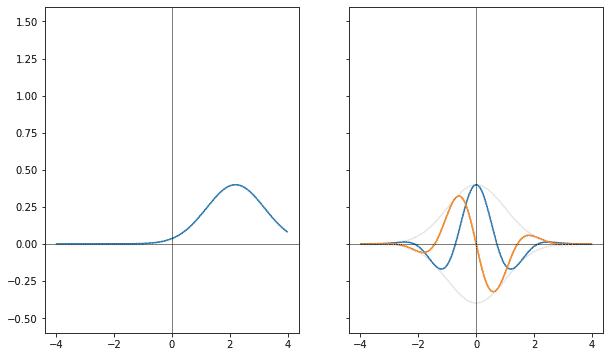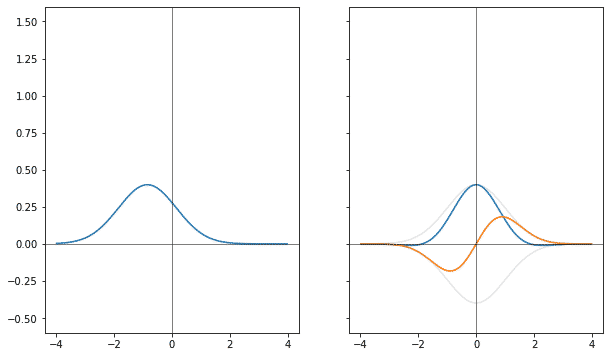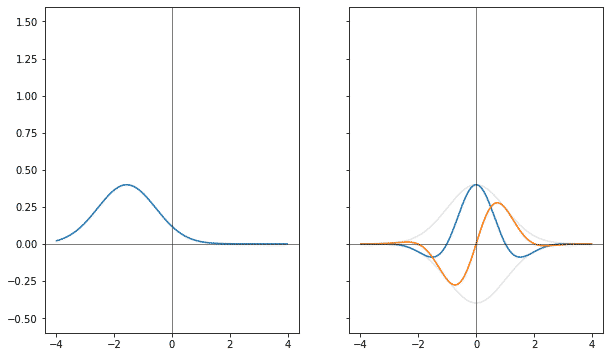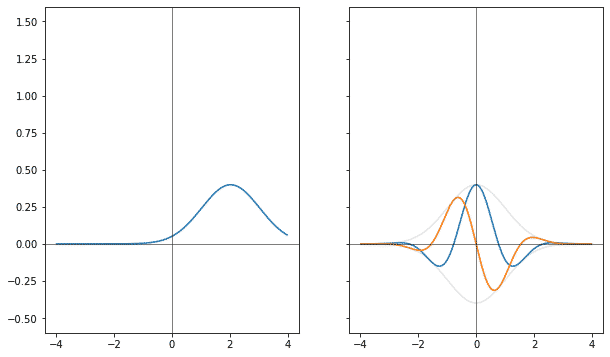
Если точно так же сворачивать гауссиану в оригинале, то фурье-образ сдвигается. Только, в обратную сторону.
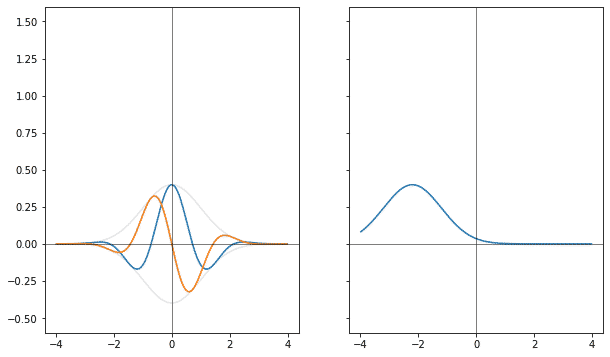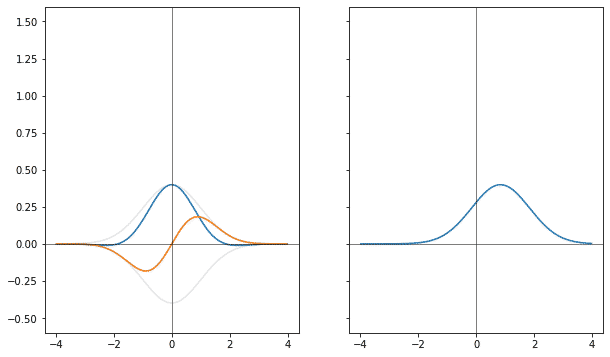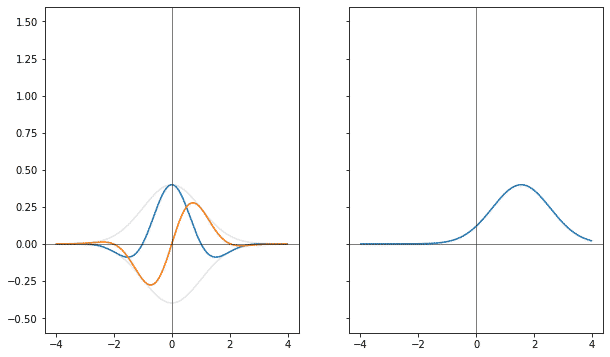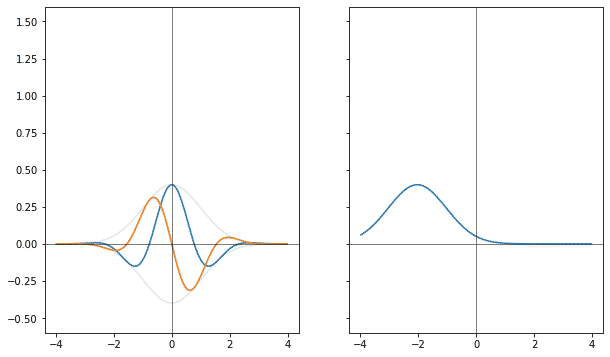
Если одну гауссиану разделить на сумму двух, и сдвигать их в разные стороны, то получится гауссиана, которая будет умножена на косинус, с частотой, соответствующей величине раздвижения.
Что будет, если попробовать применить сразу оба сдвига? Обнаружится, что если сначала сдвинуть гауссиану в пространстве, а затем сдвинуть по частоте, то получится совсем не то же самое если сначала сдвинуть по частоте, а потом в пространстве. При изменении частоты одна точка обязательно оставляет постояной свою фазу, являясь центром. И в одном случае это начало отсчёта координат, а в другом случае это центр гребня.
Для точного определения функции после двух сдвигов нужна такая процедура, которая оставляет центр сдвига фазы ровно посередине между началом отсчёта и местом гребня гауссианы. И такая процедура есть. Например, если сначала наполовину сделать первый сдвиг, потом сделать второй сдвиг полностью, а потом доделать оставшуюся часть первого, место сохранения фазы будет ровно посередине. В нулевой точке фаза сдвинется на половину величины сдвигаемой фазы назад, а в на гребне фаза сдвинется на половину вперёд.
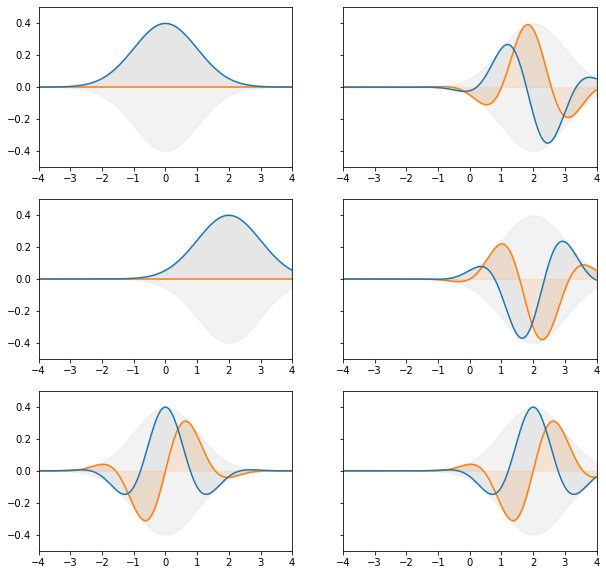
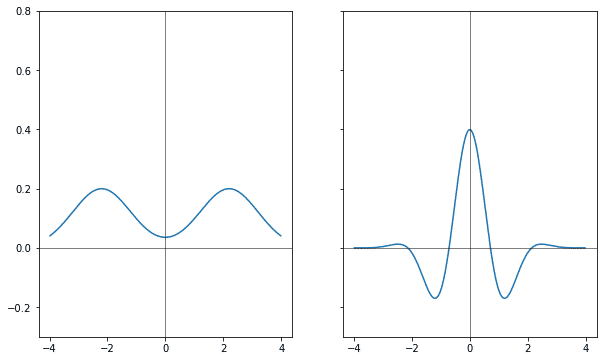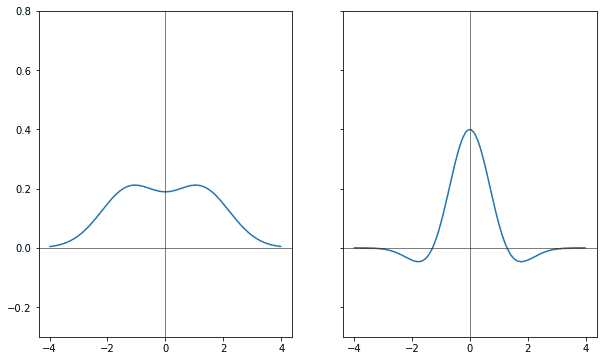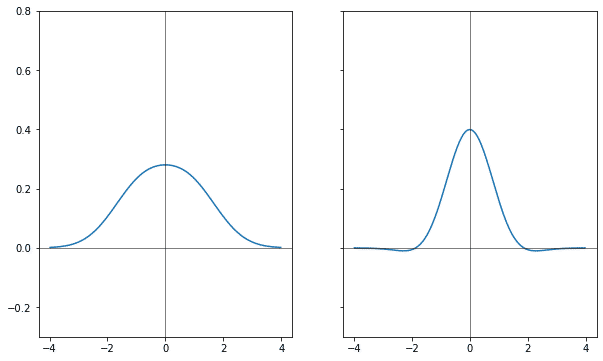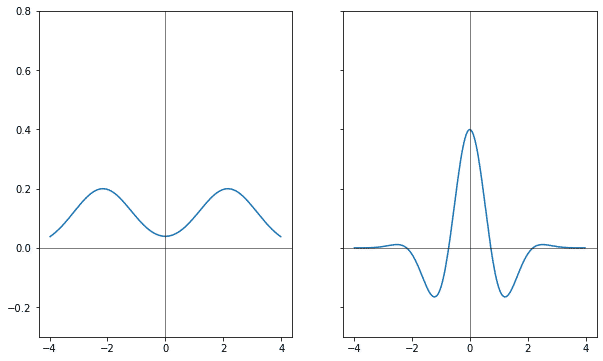
Первый график это гауссиана. Второй — результат совмещённого сдвига на величину два. Центр фазового сдвига находится в единице, содержит действительное значение. Второй ряд — результат сдвига сначала по пространству, затем по частоте. Третий ряд — сдвиг сначала по частоте, затем по пространству.
Два различных варианта представления показателя взаимозаменяемы:
Как будто это поворот на четверть круга.
Их даже можно вместе по кругу гонять.
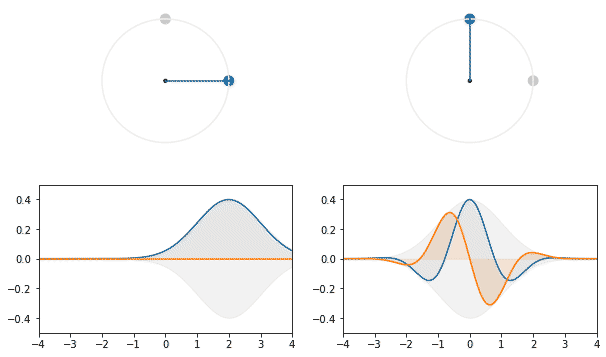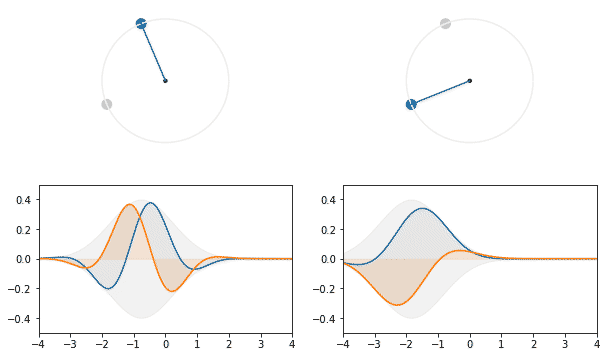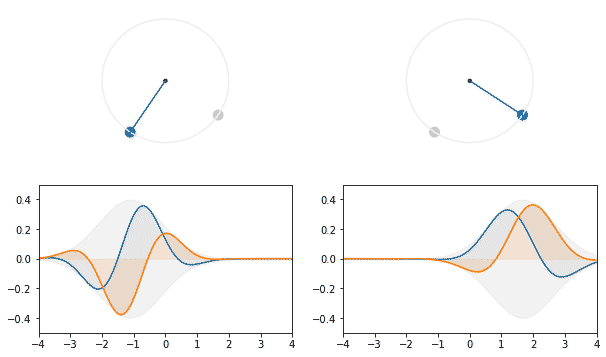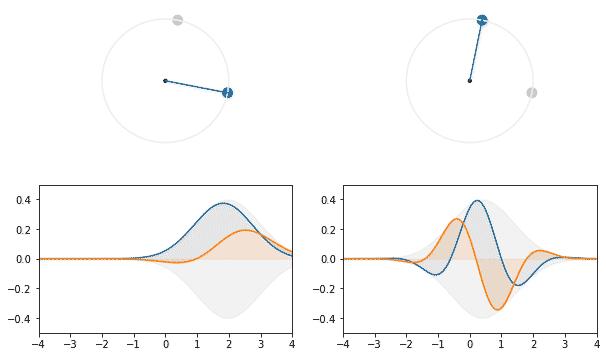
Ну, то есть, преобразование фурье гауссианы можно делать плавно.
Ради этой весёлой гифки стоило написать статью. Гауссиана испытывает плавное преобразования фурье, а из-за первоначального отклонения это выглядит как колебания вокруг центра, словно на пружинке.
А если вспомнить про свёртку и про линейность преобразования, то выходит, что для каждой функции, которая может быть разложена на гауссианы, преобразование фурье тоже можно делать плавно.
Чтобы не путать направления поворота, нужно расставить ориентиры: обратное преобразование фурье, которое по заданной частоте даёт её волновое представление, поворачивает распределение в фазовом пространстве против часовой стрелки, соответственно тому как меняется комплексное число при сдвиге фазы в положительную сторону. Прямое преобразование фурье является детектором частоты, поэтому поворачивает значение функции разложения по часовой, переводит мнимое значение комплексной координаты![$c+si$]() в действительное, с сохранением знака составляющей.
в действительное, с сохранением знака составляющей.
Если интересно, как примерно выглядит плавное преобразование фурье для одной выделенной частоты, то вот полуторамегабайтная гифка. Для приближения использована сотня гауссиан. А в этой гифке немного перераспределён масштаб времени, чтобы сборка всплеска не была слишком быстрой.
Экспериментируем дальше.
Если две гауссины между собой свернуть, то получится как будто после размытия одной процесс продолжили на величину размытия другой, и в результате получится фигура с двойным размытием. Посмотрим как это выглядит. Возьмём два гауссианы заданной ширины.
Получилась гауссиана
Если допустить, что ширина может выражаться комплексными числами, то функция, которая при свёртке должна была бы обращать размытие, будет представлена гауссианой с отрицательным квадратом ширины, то есть с мнимой величиной ширины. Рассмотрим форму графика гауссианы, задавая квадрат ширины действительным числом. Вот как выглядит переход через нулевое значение:

Менять знак у квадрата комплексных чисел можно не только проходя через ноль, значение можно повернуть в комплексном пространстве, плавно от единицы до мнимой единицы. Гауссиана тогда будет меняться так:

Интересно здесь то что при промежуточном значении![$h=\sqrt{i}=(1+i)/\sqrt{2}$]() гауссиана расправляется во всю ширь, везде с одинаковым абсолютным значением, отличаясь по пространству только комплексной фазой.
гауссиана расправляется во всю ширь, везде с одинаковым абсолютным значением, отличаясь по пространству только комплексной фазой.
А что если физика-наблюдателя и наблюдаемую микрочастицу одновременно свернуть с такой гауссианой? И частица и физик будут занимать всю вселенную, для линейных взаимодействий не фиксируя никаких изменений друг в друге. Начало волновой интуиции — в понимании того, что размытие относительно. И не только математически, но и физически.
По теме физики можно добавить ещё: усиление взаимодействия кварков с расстоянием напоминет гауссиану с отрицательным квадратом от ширины — она тоже, чем дальше от нуля, тем больше. Но это ей не мешает быть претендентом для свёртки для обращения размытия.
Будем называть гауссиану![${e^{-x^2/2}}/{\sqrt{2\pi}}$]() базовой. А гауссиану
базовой. А гауссиану ![${e^{-(x^2+(2x-c)(c-si))/2}}/{\sqrt{2\pi}}$]() смещённой. Если свернуть базовую с любой другой, то в фазовом пространстве преобразования фурье, в котором функция была сконцентрирована в одной точке, значение расплывётся вдоль линейного направления именно так как эта вторая гауссиана. После этого можно повернуть фазовое пространство на четверть оборота и затем произвести свёртку со смещённой гауссианой, чтобы получить преобразование фурье. При этом результат интеграла гауссиан с разнообразием их комплексных фаз соберётся в подтянутую гауссианту, в соответствии (обратном) изначально растолстевшей.
смещённой. Если свернуть базовую с любой другой, то в фазовом пространстве преобразования фурье, в котором функция была сконцентрирована в одной точке, значение расплывётся вдоль линейного направления именно так как эта вторая гауссиана. После этого можно повернуть фазовое пространство на четверть оборота и затем произвести свёртку со смещённой гауссианой, чтобы получить преобразование фурье. При этом результат интеграла гауссиан с разнообразием их комплексных фаз соберётся в подтянутую гауссианту, в соответствии (обратном) изначально растолстевшей.
Для обобщения можно сразу рассчитать свёртку размытия — с указанием направления размытия в фазовом пространстве.![$c$]() и
и ![$s$]() задают характеристики
задают характеристики ![$n=\sqrt{1+c^2-csi}$]() и
и ![$m=\sqrt{1+s^2+csi}$]() .
.
![$n/m$]() , а высоту через
, а высоту через ![$1/n$]() . Через
. Через ![$1/m$]() определено значение интеграла гауссианы. Как обычно, произведение ширины и высоты это площадь.
определено значение интеграла гауссианы. Как обычно, произведение ширины и высоты это площадь.
Преобразование фурье обменивает![$m$]() и
и ![$n$]() . При плавном преобразовании фурье они будут обмениваться также плавно.
. При плавном преобразовании фурье они будут обмениваться также плавно.
![$(n^2+m^2)/2$]() , а радиус вращения зависиот от
, а радиус вращения зависиот от ![$(n^2-m^2)/2$]() . Если абсолютные значения будут равны, то путь изменения будет проходить через нулевую точку, в которой — или высота, или интеграл гауссианы уходит в бесконечность. Свёртка с такой гауссианой похожа на поворот. Как при умножении чисел, когда степень у комплексного множителя ни положительная, ни отрицательная, а мнимая, происходит поворот в комплексной плоскости.
. Если абсолютные значения будут равны, то путь изменения будет проходить через нулевую точку, в которой — или высота, или интеграл гауссианы уходит в бесконечность. Свёртка с такой гауссианой похожа на поворот. Как при умножении чисел, когда степень у комплексного множителя ни положительная, ни отрицательная, а мнимая, происходит поворот в комплексной плоскости.
А если радиус превысит отклонение центра от нуля, гауссиана как будто выворачивается наизнанку, квадрат высоты и квадрат площади при обмене значениями ещё и свой знак меняют, ширину тут не может не колбасить. Свёртка с такими гауссианами была бы наведением резкости, если б сходилась.
Думаю, на этом можно закончить. Получилась, на мой взгляд, и развлекательная и познавательная статья. И пусть рассказано в основном про преобразование фурье, это достаточно большая часть волновой интуиции. Если задуматься, какую роль имеют чёткость и плавность в нашей жизни, может оказаться, что переоценить просто невозможно.
Вместо рекламы тут выражение благодарности всем кто задонатил за статью «скучные числа». Может, и эта статья кому-нибудь настолько понравится.

«Чёткость» и «Плавность» — два раздела статьи.
Чёткость
Начну с абстрактной задачи.
Представьте, что сотрудников вашего института вывели на улицу и построили в линейку. И раздали всем наборы конфет. Скажем, в наборе круглое число, 1024 конфеты, делить пополам можно аж десять раз. Но количество наборов меньше, чем количество человек и поэтому наборы достались не всем. Количество конфет очень важно на поляне чаепития, поэтому вы даёте команду: каждому, половину того что есть — отдать соседу слева. Распределение немного размылось.
И вот такой интересный вопрос: можно ли сформировать такую следующую команду по раздаче, чтобы обратить предыдущую команду, то есть, чтобы наоборот, собрать? Можно ли достичь чёткости через «размытие»? Оказывается, можно. Только, придется величину раздачи допустить отрицательной и оперировать на любом расстоянии, а не только обмениваться с соседями.
Влево надо раздавать чередуя минус и плюс. Себе оставить долю. И вправо чередуя плюс и минус. Например, если всего пять человек, то схема обмена будет такой:
Проследим за процессом. Сначала набор был только у третьего, после первого обмена конфеты есть у второго и третьего. Следующий обмен рассчитывается суммированием единиц со знаком, взятым из таблицы, умножив строчку на количество конфет у соответствующего сотрудника. То есть, используется только вторая и третья строка и останется просуммировать по колонкам. Все колонки кроме третьей суммируются в ноль — весь набор конфет собирается обратно, третьему. Все отрицательные раздачи лишние, и компенсируются лишними положительными. Алгоритм работает.
Тут есть пара проблемок. Первая: непонятно, кому же отдаст половину самый левый. Но это решить просто, надо изначально левому не давать конфет. Хех. Ну, или пусть отнесёт самому правому, то есть, линейку можно зациклить.
А вторая проблемка: алгоритм хорошо работает для нечётного количества человек, а если число чётное, то уже нет. Ну, представьте что у вас всего два человека, после первого распределения у них всегда оказывается количество одинаковое, и какая часть от кого перешла — никак не восстановить.
И, например, для четырёх человек можно заметить, что распределение плюсов и минусов при зацикливании начинает противоречить само себе: знаки при наложении соседних циклов противоположны. Так что, остаётся только использовать алгоритм для пяти, но пятый участник будет отсутствовать: то есть, ни раздавать конфеты, ни получать.
Надеюсь, бесконечность не является чётной? А то, в этом случае обобщить на линейку с бесконечным количеством элементов может и не получиться. Думаю, надо обязательно, чтобы этот сотрудник, попавший на линейку на бесконечное место, гарантированно не участвовал в обмене. И все его соседи тоже. А может, бесконечность тем и отличается, что можно рассчитывать на тот вариант, который получше? Тогда — пожалуйста, пусть она будет нечётная. Тогда в обмене будут участвовать все.
Это важный момент — один лишний отсчёт и точное восстановление в общем виде не работает, появляюся варианты.
(* Вставить иллюстрацию, промт: одинокий сотрудник стоит на «бесконечном месте», никаких конфет, темно.)
Свёртка
При переходе с шутливых аналогий на математическое описание надо рассказать о понятии свёртка. Это именно то что происходило при команде поделиться конфетами. Сама операция свёртки — это операция над двумя функциями, которая даёт третью, в которой каждое из значений первой линейно перераспределено по схеме из второй.
Например, эхо. Это же свёртка функции того что вы крикнули и схемы повторения. Или, например, если в небе происходит солнечное затмение, то тень становится покрытой множеством маленьких солнечных месяцев. Результат здесь — это свёртка того что видно в небе и схемы расположения отверстий в преграде для света.

Математически это выражается так:
Или можно применить нечто среднее:
Самое характерное свойство у свёртки это линейность, оно выражается в том что если взять две функции, каждую свернуть с третьей и потом результаты сложить, то это будет то же самое как если бы функции сначала были сложены, а потом была произведена свёртка. То есть, не важно когда складывать, до свёртки или после.
К этому моменту у нас кроме начального распределения есть пара функций: функция размытия и функция возвращения резкости. Свёртка со второй — обращает свёртку с первой.
Множество шагов размытия
Размывающее распределение «отдай соседу половину» можно повторять много раз. Раздачу лучше чередовать влево и вправо, тогда после каждой такой пары начальный элемент будет оставаться в центре распределения. Ситуацию можно рассмотреть только с одним установленным вначале элементом, остальные варианты получаются свёрткой. Посмотрим на формулу для расчёта значений, которые получаются сразу на выбранном шаге.
Если при каждом делении дополнительно умножать на два, тогда значение элемента будет просто суммой предыдущего значения элемента и предыдущего значения соседнего элемента, со стороны с которой передают. Тогда самый крайний элемент такого распределения будет оставаться единицей. А первый соседний элемент будет суммой таких единиц, выполненных столько раз, сколько прошло шагов. Значит, равно количеству шагов.
Следующий, второй соседний элемент, точно так же последовательно суммирует предыдущие суммы. И дополнительно нужно учесть, что в цепочке суммирования последнее слагаемое будет на единицу меньше, чем номер шага, поэтому формула второго элемента будет
Чтобы получить третий элемент нужно умножить второй на
Теперь останется отменить умножение на два на каждом шаге — поделить на двойку в степени номера шага — и значение результата размытия будет получено. Расчёт в случае отсчёта позиции от крайнего элемента:

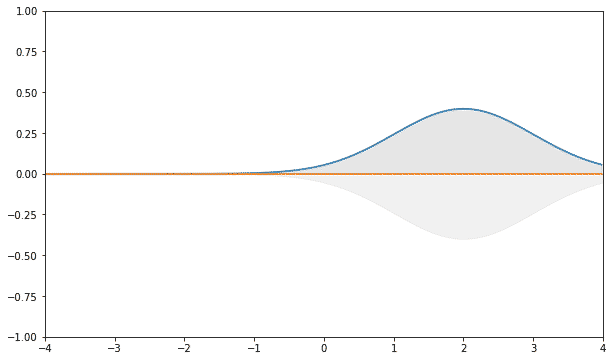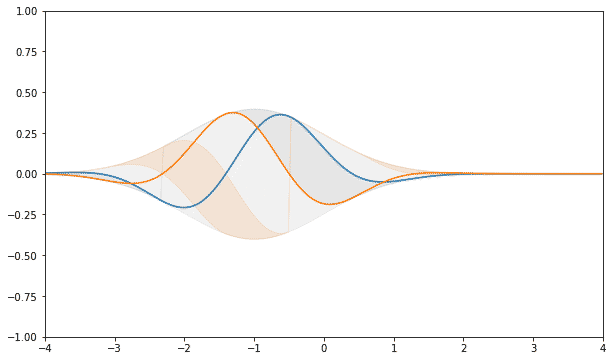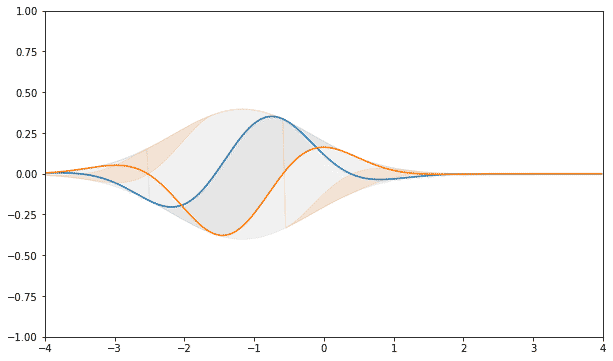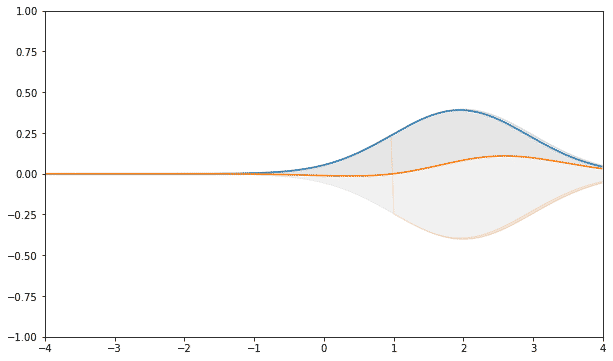
И вот тут такой вопрос — при увеличении шагов этот холмик расширяется или сужается? С одной стороны размытие это расширение в разные стороны. С другой стороны, взгляните график распределения распределения после 200 шагов.

Относительно всей области размытия холмик выглядит как узенький всплеск посередине, относительно всей широты фигура с каждым шагом только сужается.
Если на масштабе одного элемента распределение расширяется, а на масштабе всей области распределение сужается, то сохраняется фигура холмика с увеличением шагов только на среднем масштабе. Ориентировочные размеры — это корень из количества шагов. Или, наоборот, количество шагов соразмерно квадрату от количества делений для выбранной ширины.
При увеличении шагов до бесконечности на среднем масштабе распределение приближается к функции Гаусса. Вы встречали в фотошопе «размытие по Гауссу»? Это многократно повторяющееся размытие на один пиксел, которое приводит к замутнению картинки. Если не брать во внимание сдвиг от центра и всевозможные коэффициенты для аргумента и для значения, формула гауссианы будет такой:
Пусть у среднего элемента индекс
Дальше считаем интеграл функции, чтобы нормировать до единицы, как у первоначального элемента. Производная от
Нормированная гауссиана
Теперь можно задаться вопросом, как в таком же пределе выглядит отрицательное количество шагов размытия.
Множество шагов наведения резкости
Для того чтобы получить схему распределения для отмены двух шагов размытия нужно свернуть функцию для шага обращения размытия с ней же самой.

Диаграмма применения второго шага наведения резкости по принципу первой диаграммы (из плюсов и минусов), но уже с применённым изменением знака, в соответствии с множителем внутри свёртки. Светлым обозначен плюс, тёмным минус. Описать расстановку можно так: знак зависит от чётности места получателя, и у тех мест что ниже диагонали знак изменён на противоположный. Суммирование по колонкам приводит к распределению: одно из значений равно количеству элементов в линейке, и отдаляющиеся от неё в обе стороны — уменьшаются по абсолютной величине на два, и ещё меняют знак, сходясь до минус единиц на двух противоположных ему в цикле элементах.

При дальнейшем наведении резкости знак в расстановке так и продолжит чередоваться. Эту постоянную смену знака можно исключить из внимания, оставив только положительные значения на каждом шаге. Меняем знак у колонок с нечётным индексом на противоположный. Тогда, на этом же примере, можно подсчитать, что суммы по колонкам будут от -9 до 11 с шагом 2. Но все числа распределения теперь же уже положительные, что делать с отрицательными? В получившуюся функцию отрицательные числа не попадают, потому что с каждым шагом схема чередования знака сдвигается — и для мест, где знак отрицательный он при этом меняется.
Если количество шагов размытия превысит количество элементов, то конечно, значения, разошедшиеся в разные стороны, снова сойдутся и произойдёт наложение. Для вычисления соответствующего наведения резкости это дополнительно усложнило бы распределение. Но восстанавливающие значения расстановки для этого случая всё равно существуют и работают.
На одиннадцати элементах третий шаг наведения резкости приводит к таким значениям:
При рассмотрении размытия был интересен масштаб для стабилизации холмика. Здесь же значения занимают всю линейку, какой бы она ни была, и уже на третьем шаге нет ни одного значения меньше, чем количество элементов. Никаких холмиков здесь не наблюдается. Тогда, какие же здесь закономерности? Ну, кроме уже принятого во внимание чередования знака.
Первый шаг наведения резкости выражается просто.
На третьем шаге форма распределения парабола.
Для перехода на следующий шаг нужно из выражения для предыдущего уровня вывести выражение суммы диапазона элементов. Так как зависимость значений от

Пятый шаг:
Переориентируем систему отсчёта так:

Ну что, пятый шаг выполнен, бесконечность — уже совсем близко.
Можно подумать, что график распределения это косинус, но он может совпадать с ним только в пределе. При ограниченном количестве шагов всегда есть очень важное, даже принципиальное отличие.
Немного усилий
Будем использовать формулу для суммы.
![$(B_j$]() — это числа Бернулли)
— это числа Бернулли)
И обычный бином Ньютона.
![$n^b$]() . Суммирование:
. Суммирование:
![$n$]() в нужной степени нужно рассчитать значение вклада при выбранном
в нужной степени нужно рассчитать значение вклада при выбранном ![$y$]() :
:
И обычный бином Ньютона.
Получилась вот такая общая формула:
Но зачем заходить так далеко?
Можно просто просуммировать коэффициенты, используя закономерность.
![$x$]() и
и ![$n$]() можно поменять между собой.
можно поменять между собой.
Для коэффициентов пересчёт будет таким:![$n=0$]() , а место смены чередования знака лежало при
, а место смены чередования знака лежало при ![$x=0$]() . Но каждый раз при расчёте свёртки максимум сдвигается на половину линейки. И значит, что при расчёте расстановки чередуются и действительные координаты — это то
. Но каждый раз при расчёте свёртки максимум сдвигается на половину линейки. И значит, что при расчёте расстановки чередуются и действительные координаты — это то ![$x$]() , то
, то ![$n$]() . Для такой стабилизации надо чередовать направления сдвигов размытия. Максимум распределения при отсутствии компенсации чередования знака будет то положительным максимумом то отрицательным минимумом. Ещё, чтобы получить расстановку кроме возвращения правильного знака нужно, как и в формуле для размытия, поделить на 2 в степени номера шага.
. Для такой стабилизации надо чередовать направления сдвигов размытия. Максимум распределения при отсутствии компенсации чередования знака будет то положительным максимумом то отрицательным минимумом. Ещё, чтобы получить расстановку кроме возвращения правильного знака нужно, как и в формуле для размытия, поделить на 2 в степени номера шага.
Для коэффициентов пересчёт будет таким:
Ещё одна заметка
На основе того, что преобразования координат туда и обратно не меняет значения, можно обнаружить, что сумма по определёной выборке равна нулю:
![$\sum_{k=0}^n (-1)^k C_n^k = \delta_n$]() — если у биномиальных коэффициентов при суммировании чередовать знак, то в сумме получится ноль. Коэффициенты получены размытием, и теперь его части компенсируют друг друга. А если коэффициент только один, то результат станет единицей, потому что размытия в этом случае не было.
— если у биномиальных коэффициентов при суммировании чередовать знак, то в сумме получится ноль. Коэффициенты получены размытием, и теперь его части компенсируют друг друга. А если коэффициент только один, то результат станет единицей, потому что размытия в этом случае не было.
Этого для поверхностного представления того как выглядит изнанка размытия хватит.
Объединяем направления
Наведение резкости можно назвать отрицательной степенью размытия. Если подставить в формулу
Между размытием и резкостью есть ещё одно общее свойство — постоянное значение они оба переводят в постоянное значение. Но если для размытия это выглядит как суммирование соседних значений и затем деление на два — что для одинаковых значений возвращает к нему же — то для резкости расчёт происходит немного по-другому.
Если мы знаем, что элемент чёткой линейки равен
У линейки можно отделить общее постоянное значение, чтобы его пересчитывать на следующий шаг просто добавлением, не проводя через расчёты. При таком отделении от линейки размером

С постоянным значением всё просто. Но кроме постоянного значения есть и другие формы распределения, которые при размытии не меняют формы.
Что будет если вы сложите две синусоиды, которые не отличаются ни амплитудой, ни частотой, а только фазой? Если фазы будут не противофазами друг другу, то результат тоже будет синусоидой, с той же частотой. Поэтому, если распределение будет гармонической функцией по частоте кратной размеру линейки, то и при размытии и при резкости она останется гармонической функцией той же частоты, поменяв только амплитуду.
В полном соответствии со школьной формулой
Думаю, сильно заметно, что после пары одинаковых шагов размытия центр на один отсчёт уплывает, постоянно приходится следить куда уплыл. Пора вводить третью координату, которая остаётся нулём в месте центра размытия.
Новая координата такая:
Перепишем предыдущую формулу для новой координаты. Теперь операции над гармонической функцией записываются однообразно. Для размытия нужно умножить, а для резкости, соответственно, поделить:
Тут может заинтересовать функция, которая остаётся после отделения всех гармонических составляющих.
Как отделять частотные составляющие? Чтобы рассчитать одну из них нужно просуммировать функцию, умножив на косинус заданной частоты и отдельно просуммировать, умножив на синус заданной частоты.
Собрать из косинусов можно любой отдельный отсчёт, нужно лишь чтобы сдвиг фазы у всех косинусов помещал гребень на него. А это значит, что любое распределение полностью раскладывается на гармонические функции, без остатка.
Используя такое разложение на косинусы, вместе с полученным выше расчётом для косинуса одного шага размытия, можно вывести выражение для расчёта расстановок для любого количества шагов размытия одного элемента.
Какая симпатичная формула получилась, простая и ясная, мне нравится. Теперь для распределения имеется три формулы: для размытия, для резкости и общая, которая позволяет расчитать результаты для обеих.
У этого варианта есть одно дополнительное свойство. Похоже, расстановку можно так определять не только для целых, но и для действительных значений — как для позиции, так и для степени размытия.
Количество элементов
Задаётся он через отношение суммы из таких околонулевых значений элементов, которые соответствуют единице, и количеством суммируемых элементов. Коэффициент стремится к нулю, но ему не равен. Множитель
Превратим общую формулу размытия в интеграл. Дробь
Я сразу решил посмотреть, как выглядит Гауссиана, выраженная как предел бесконечности шагов размытия с сохранением масштаба.
Как собирать распределение из гармонических функций для неограниченного числа элементов — ясно, а как его на эти гармонические функции разбирать?
Если начальный элемент будет не по нулевой координате, то его распределение будет содержать не только косинусы — фаза будет сдвинута, а значит, и синусы появятся. Значит, при разборе распределения нам опять понадобится отдельно выявлять косинусы и отдельно синусы. И после этого у нас получится целых два значения. Лучше это сразу объединить в одно.
Стоит использовать комплексные числа, и вместо двух функций результата иметь одну функцию, значение у которой содержит одно комплексное число, две составляющих, реальную и мнимую. Кроме того, сама гармоническая функция может быть выражена как косинус в реальной части и синус в мнимой.
Реальная часть разделяемой функции при умножении на реальную часть гармонической функции будет выделять косинус, а при умножении на мнимую часть гармонической функции будет выделять синус, и в результате число, которое получено, само определяет амплитуду и фазу, своим модулем и аргументом.
Кроме этого, мнимая часть разделяемой функции при умножении на мнимую часть гармонической функции будет образовывать отрицательный вклад в реальную часть результата, и при умножении мнимой на реальную в мнимой части результата тоже будет вычет. Но из-за того что детектируемые частоты разделяются на отрицательные и положительные, через то что у синуса в мнимой части различный знак, по итогу детектируется именно нужная частота, а противоположная, если её там нет, приводит к нулевому результату.
Для того чтобы определить составляющую нужно умножать на гармоническую функцию — но не той частоты, которая при этом определяется, а противоположной по знаку. Потому что произведение со значением с обратной частотой приводит к противодействию вращению в комплексном пространстве, и элементы суммы перестают кружить вокруг нуля, давая в результате суммирования не нулевое значение.
Сбор расстановки из гармоник:
Но интегралом разбор тоже может быть, потому что в «плавном представлении» каждый отсчёт свёрнут с функцией
Здесь уже можно отметить: свёртка двух расстановок будет давать такую же раскладку как произведение соответствующих раскладок от этих двух функций. Например, размытие получается свёрткой заданной расстановки с расстановкой размытия, но при сборе из гармоник раскладка из косинусов, которая получилась бы без размытия, умножается на косинусы, которые сами являются раскладкой от размытия. Короче,

Эти преобразования можно сделать однообразными, использовав вместо суммы интеграл и избавившись от коэффициента перед частотой в показателе в выражени для
После этого образовавшийся общий коэффициент перед интегралом можно раскидать между прямым и обратным преобразованием, будет:
Первая функция, которая испытает преобразования Фурье на себе, у нас будет, конечно же, гауссиана.

Если проследить за тем как постепенно с каждым шагом размытия косинус превращается в экспоненту, то можно увидеть, как от него удаляется второй гребень, и меняется при этом в знаке, соответственно степени от отрицательного числа.

В общем, интересный получился предел.
Плавность
Теперь, когда преобразование фурье выведено, мы займёмся дальнейшими экспериментами над гауссианой.
Эталонная гауссиана не меняется при преобразовании фурье, и её фурье-образ с ней совпадает.

С общим множителем преобразование ничего не делает, оставляет каким был.

Если через коэффициент к аргументу у гауссианы менять ширину, расширять, то её фурье-образ меняется сразу в двух направлениях: он и сужается и растёт.

Используя линейность преобразования можно изменение высоты распределить между исходником и результатом преобразования, тогда получится, что когда одна из функций растёт, другая уменьшается.

Следующий эксперимент — со сдвигом.

Если точно так же сворачивать гауссиану в оригинале, то фурье-образ сдвигается. Только, в обратную сторону.

Если одну гауссиану разделить на сумму двух, и сдвигать их в разные стороны, то получится гауссиана, которая будет умножена на косинус, с частотой, соответствующей величине раздвижения.

Что будет, если попробовать применить сразу оба сдвига? Обнаружится, что если сначала сдвинуть гауссиану в пространстве, а затем сдвинуть по частоте, то получится совсем не то же самое если сначала сдвинуть по частоте, а потом в пространстве. При изменении частоты одна точка обязательно оставляет постояной свою фазу, являясь центром. И в одном случае это начало отсчёта координат, а в другом случае это центр гребня.
Для точного определения функции после двух сдвигов нужна такая процедура, которая оставляет центр сдвига фазы ровно посередине между началом отсчёта и местом гребня гауссианы. И такая процедура есть. Например, если сначала наполовину сделать первый сдвиг, потом сделать второй сдвиг полностью, а потом доделать оставшуюся часть первого, место сохранения фазы будет ровно посередине. В нулевой точке фаза сдвинется на половину величины сдвигаемой фазы назад, а в на гребне фаза сдвинется на половину вперёд.

Первый график это гауссиана. Второй — результат совмещённого сдвига на величину два. Центр фазового сдвига находится в единице, содержит действительное значение. Второй ряд — результат сдвига сначала по пространству, затем по частоте. Третий ряд — сдвиг сначала по частоте, затем по пространству.
Два различных варианта представления показателя взаимозаменяемы:
Как будто это поворот на четверть круга.
Их даже можно вместе по кругу гонять.

Ну, то есть, преобразование фурье гауссианы можно делать плавно.

Ради этой весёлой гифки стоило написать статью. Гауссиана испытывает плавное преобразования фурье, а из-за первоначального отклонения это выглядит как колебания вокруг центра, словно на пружинке.
А если вспомнить про свёртку и про линейность преобразования, то выходит, что для каждой функции, которая может быть разложена на гауссианы, преобразование фурье тоже можно делать плавно.
Чтобы не путать направления поворота, нужно расставить ориентиры: обратное преобразование фурье, которое по заданной частоте даёт её волновое представление, поворачивает распределение в фазовом пространстве против часовой стрелки, соответственно тому как меняется комплексное число при сдвиге фазы в положительную сторону. Прямое преобразование фурье является детектором частоты, поэтому поворачивает значение функции разложения по часовой, переводит мнимое значение комплексной координаты
Если интересно, как примерно выглядит плавное преобразование фурье для одной выделенной частоты, то вот полуторамегабайтная гифка. Для приближения использована сотня гауссиан. А в этой гифке немного перераспределён масштаб времени, чтобы сборка всплеска не была слишком быстрой.
Экспериментируем дальше.
Если две гауссины между собой свернуть, то получится как будто после размытия одной процесс продолжили на величину размытия другой, и в результате получится фигура с двойным размытием. Посмотрим как это выглядит. Возьмём два гауссианы заданной ширины.
Подробный вывод
Переобозначим на коэффициенты частоты
![$v$]() , в другой заменив аргумент на
, в другой заменив аргумент на ![$(x-v)$]()
После этого под интегралом можно оставить только степень с переменной интегрирования, остальное вынести из интеграла.
![$\pi$]() , умноженного на коэффициент перед переменной интегрирования в показателе, включая деление на два, это добавляет двойку перед
, умноженного на коэффициент перед переменной интегрирования в показателе, включая деление на два, это добавляет двойку перед ![$\pi$]() . Результат будет
. Результат будет
После этого под интегралом можно оставить только степень с переменной интегрирования, остальное вынести из интеграла.
Получилась гауссиана
Если допустить, что ширина может выражаться комплексными числами, то функция, которая при свёртке должна была бы обращать размытие, будет представлена гауссианой с отрицательным квадратом ширины, то есть с мнимой величиной ширины. Рассмотрим форму графика гауссианы, задавая квадрат ширины действительным числом. Вот как выглядит переход через нулевое значение:

Менять знак у квадрата комплексных чисел можно не только проходя через ноль, значение можно повернуть в комплексном пространстве, плавно от единицы до мнимой единицы. Гауссиана тогда будет меняться так:

Интересно здесь то что при промежуточном значении

А что если физика-наблюдателя и наблюдаемую микрочастицу одновременно свернуть с такой гауссианой? И частица и физик будут занимать всю вселенную, для линейных взаимодействий не фиксируя никаких изменений друг в друге. Начало волновой интуиции — в понимании того, что размытие относительно. И не только математически, но и физически.
По теме физики можно добавить ещё: усиление взаимодействия кварков с расстоянием напоминет гауссиану с отрицательным квадратом от ширины — она тоже, чем дальше от нуля, тем больше. Но это ей не мешает быть претендентом для свёртки для обращения размытия.
Характеристики
Будем называть гауссиану
Для обобщения можно сразу рассчитать свёртку размытия — с указанием направления размытия в фазовом пространстве.
Преобразование фурье обменивает
А если радиус превысит отклонение центра от нуля, гауссиана как будто выворачивается наизнанку, квадрат высоты и квадрат площади при обмене значениями ещё и свой знак меняют, ширину тут не может не колбасить. Свёртка с такими гауссианами была бы наведением резкости, если б сходилась.
Думаю, на этом можно закончить. Получилась, на мой взгляд, и развлекательная и познавательная статья. И пусть рассказано в основном про преобразование фурье, это достаточно большая часть волновой интуиции. Если задуматься, какую роль имеют чёткость и плавность в нашей жизни, может оказаться, что переоценить просто невозможно.
Ссылки на другие мои статьи
Cортировка по степени рекомендации.
- «Экскурсия в подвал» — как выглядит подвал математики.
- «????-повар и ????-торт» — о том что у числа ???? есть простая формула.
- «Скучные числа» — обо всех числах. Натруальные числа, дроби, иррациональные, бесконечность, i, e, ????, ????, числа бернулли, нули дзета-функции.
- «Как устроены волны» — до конца не объяснено, но что есть — интересно.
- «Удивительная и загадочная ????» — кроме e и ???? есть ещё «круглые» константы.
- «Взгляд программиста на гипотезу Коллатца» — развлекательная переформулировка гипотезы.
- «Простое и точное решение задачи про колодец лотоса» — задача с виду простая, а решит не каждый.
- «Новые нули дзета-функции» — недоказуемое веселье.
- «Тридцать шесть градусов красоты» — подробный разбор мозаики пенроуза, из приведённого кода можно собрать рисующую программу.
- «Гипотеза Эскобара» — о том что не всё просто. Кватернионы, функция ламберта, константа эйлера-маскерони. А поставленный вопрос не решён.
- «Искусственная соображалка без фатальных недостатков без нейросетей разработать» — мечта об искусственной соображалке. Обзорная статья, тег «философия». Голосование читателей — «Статья в основном безвредна». Написано в 2019, до GPT. Со временем стала только актуальней.
- «Два вида последовательного перебора пикселей» — дербаним плоскость на отдельные квадраты, расположенные последовательно.
- «Чаепитие из rvalue» — взгляд на аспект C++ как на сказку. Статья «шаблонно» заминусована.
- «Раскрытие заговора против себя дураки отложили на неопределённый срок» — попытка поумничать. По дате это май 2021-го.
- «Сто-пятьсот цифр числа пи на коленке» — как в экселе подсчитать до тысячи цифр числа пи.
- «Не простая координатная система, а золотая» — статья из песочницы, о десятиугольной системе координат.
- «Не сломать, не потерять» — скучная статья про шар. Комментарии и то веселее.
- «Общая схема» — Статья у которой на обложке кот. Находится в хабе «чулан». Внутри очень неаккуратно поданная философия.
Вместо рекламы тут выражение благодарности всем кто задонатил за статью «скучные числа». Может, и эта статья кому-нибудь настолько понравится.
Комментарии (13)

vvzvlad
00.00.0000 00:00-1Получилась, на мой взгляд, и развлекательная и познавательная статья.
Я: не понял ничего, не говоря уж о развлечении

uchitel
00.00.0000 00:00Статья классная. Свертки еще используются для "арифметических" операций над распределениями плотности вероятности. Там тоже все очень интересно получается, настолько, что на интуицию даже не стоит полагаться.

dprotopopov
00.00.0000 00:00Мне тоже одно время интересовали свёртки - в том числе фурье - даже статейки накропал
https://habr.com/ru/post/597715/

Refridgerator
00.00.0000 00:00Эта картинка однозначно имеет отношение к Chirp Z-transform:
Я также слышал о Fractional Fourier transform, но не вникал в его суть для понимания того, как оно соотносится с содержанием вашей статьи.


longclaps
Много букв, внимательно почитаю позднее. Однако.
У нас дискретная система, N коробок по 1024 конфет, 1024 сладкоежек. Есть устойчивое равновесие - когда по N конфет у каждого. Но даже если оно недостижимо - ввиду конечности числа состояний по принципу Дирихле система рано или поздно зациклится. При этом начальное состояние не обязательно будет содержаться в финальном цикле. Т.е. после достаточно большого числа итераций провернуть фарш назад не получится.
У меня вышло мало букв, я что-то упустил?
p.s. не рассчитывайте на мой быстрый ответ - мне карма не позволяет ????
p.s.s. зато пока могу здесь добавить - я утверждаю, что открутить назад может не получиться при любом числе участников, нечетность не рулит.
yurixi Автор
Да, ниже говорится, что для возможности всё обратить важно чтобы количество количество участников было нечётным.
ksbes
И что? В этом случае не возможен цикл не включающий начальное состояние? Ну, если выражаться иначе, нет состояний в которое можно прийти двумя различными путями?
Если это так, то это совсем не очевидно!
yurixi Автор
Циклы возможны, но откатив на столько же шагов получим точно то же состояние. А если количество нечётное, даже два, то даже первый шаг не обратить.
ksbes
Вы, может быть, не совсем поняли о чём идёт речь. Если у нас есть состояние В, непосредственным предшественником которого является как состояние А, так и состояние Б, то как вы выберете в какое возвращаться?
Не все дискретные автоматы обратимы — та же игра Жизнь, например: вы в ней далеко не всегда сможете "мясорубку назад провернуть".
Т.е. обратимость надо обосновывать отдельно.
yurixi Автор
Размытие напополам с соседом при нечётном количестве участников с зацикливанием по пространству участников обратимо. Двух предшественников быть не может, есть однозначный алгоритм вычисления предшественника. Их в статье даже несколько, с одинаковым результатом.
ksbes
Хорошо. Значит я не совсем понял о чём речь :) (но вообще рациональное количество конфет — это читерство!)
yurixi Автор
Не зря статья позиционирует себя как развитие интуиции.
Вас ждёт забавное открытие. Ну, или меня, если вы хоть как-то примерно намекнёте на особые случаи, когда это не получается.
Для уточнения: после деления пополам конфет может быть не целое число, это ограничение мной не учитывается.