Пакет геометрического моделирования (называемый также геометрическим ядром) — набор библиотек с программным интерфейсом (API), с помощью которого можно пользоваться функциями геометрического (например, твердотельного) моделирования. Типичной функциональностью пакета геометрического моделирования является предоставление набора программных интерфейсов (структур данных, функций и классов) для создания приложения каркасного, поверхностного, твердотельного или немногообразного моделирования. Перечислим названия некоторых из них: Parasolid, ACIS, C3D.
В некоторых производственных процессах острые углы не могут или не должны быть произведены, что автоматически порождает необходимость скруглений всех острых углов в САПР. Проблема скругления (сглаживания) очень важна, потому что занимает внушительную часть времени создания модели – обычно до 40% для подготовки деталей для литья, ковки или штамповки листового металла.
Грань скругления может базироваться на цилиндрической, конической, тороидальной или кинематической поверхности.
Сглаживание граней. Построение поверхности сопряжения между двумя наборами граней. Грани в каждом наборе должны быть связанны и в точках сочленения иметь, по крайней мере, G1-непрерывность.
G1-непрерывность.
G1 - Tangent Continuity – соединение по касательной. При такой непрерывности совпадают не только конечные точки кривых или поверхностей, но и касательные к этим точкам. И хотя этот тип соединения не допускает острых ребер, все же оно не дает идеально гладкого сопряжения.
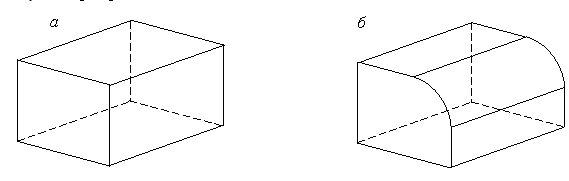
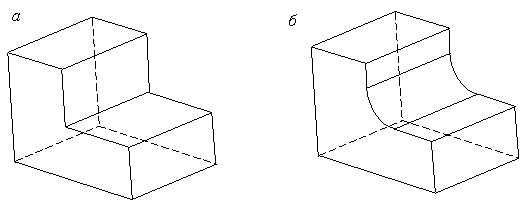
Имеют место случаи, когда требуется скруглить сразу несколько стыкующихся друг с другом ребер. Стыкующиеся ребра называют сопряженными, если в точках стыковки они имеют общую касательную. Если в точках стыковки ребра претерпевают излом, то такие ребра называют несопряженными.
При скруглении нескольких несопряженных ребер тела скругления выполняют последовательно одно за другим. В случаях скругления нескольких сопряженных ребер различные стадии операции скругления каждого ребра следует выполнять одновременно для нескольких ребер. Перед началом операции скругления следует составить группы гладко стыкующихся ребер и далее работать с этими группами как с отдельным ребром, описанным выше образом.
Если скруглить три ребра, стыкующихся в одной вершине, то такую вершину также скругляют. Скруглить вершину можно описанным выше способом: ребро пересечения двух граней скругления сопряжено с третьим ребром и может быть скруглено вместе с ним.
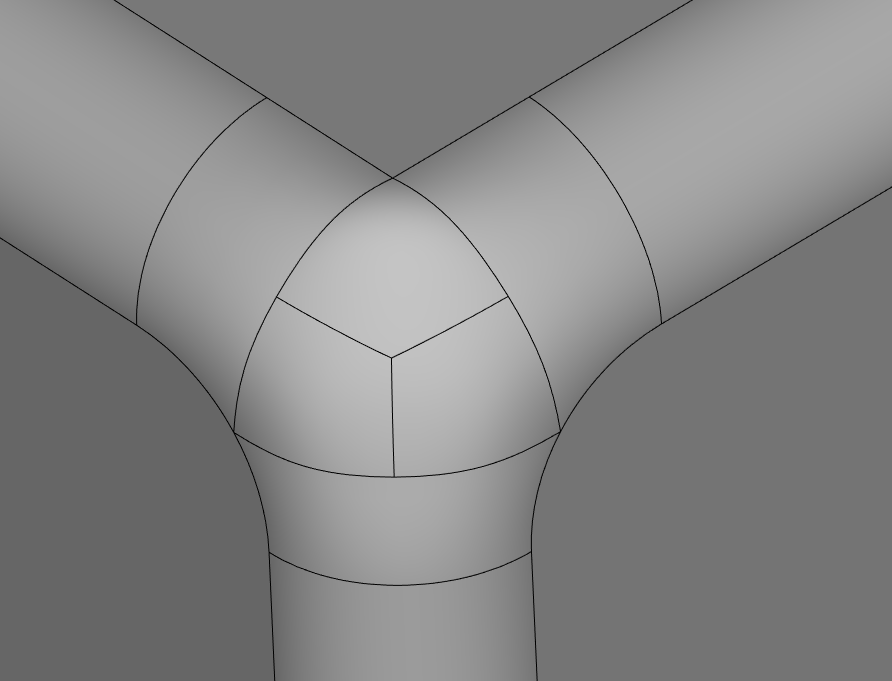
Отдельную сложность представляет собой скругление звезд (рис. 3). В некоторых случаях требуется скруглить несколько ребер, стыкующихся в общей вершине. Если в вершине стыкуется более трех ребер, то такую комбинацию ребер и вершины называют звездой. Если все ребра звезды подлежат скруглению, то, как и для группы сопряженных ребер, различные стадии операции скругления следует выполнять одновременно для всех ребер звезды и сопряженных с ними ребер. При этом звезда через сопряженные ребра может стыковаться с другими звездами. Поэтому перед началом операции скругления следует найти группы гладко стыкующихся ребер, затем звезды для них, определить группы связанных звезд и далее описанным выше образом работать с этими группами звезд как с единым объектом.

Радиус скругления может меняться по длине скругляемого ребра. В этом случае моделируют грань скругления с переменным радиусом (рис. 4). При построении скруглений с переменным радиусом следует задать функцию изменения радиуса по длине ребра.

Изменение радиуса сглаживания может быть линейным или гладким. При линейном изменении изменение радиуса описывается ломаной. При гладком – изменение радиуса задаётся кривой, имеющей в начальной и конечной точках ребра.
Иногда необходимо отступить от вершины и сформировать так называемый SetBack, т.е. дополнительную поверхность до заплатки, закрывающей вершину.
Если вам было интересно, то могу продолжить тему сглаживания, добавить больше математики и формул. Буду благодарен за обратную связь, спасибо.


ABHuman
Про внушительную часть времени создания модели явно пошутили.
У литья явно важнее литейные углы, поднутрения и правильный разъём.
Ковка и штамповка вообще больше на зазорах и пружинении заморачиваются, но никто не закладывает в модель утоньшение толщины листа и т.п. эффекты, поэтому бессмысленно прорисовывать какие-то особые условия. Всё закладывается за счёт правильного проектирования штампа, а там скругления и 4% времени не занимают.
Вот где реально есть заморочки со скруглением, так это при поверхностном моделировании и дизайне, туда же частично входит реверс-инжиниринг с использованием 3Д-сканирования. Но скругления там интереснее по g2 и по g3. И тогда уже на различимость накладывают "зебру" для оценки. И последнее ещё интереснее, ибо далеко не все твёрдотелы могут позволить правильно соединять лоскутки поверхностей и скруглять переходы.