В сети в последнее время регулярно мелькают статьи типа - как обучить Stable Diffusion генерировать ваши фотографии/фотографии в определенном стиле/фотографии определенного лора/такие фотографии итп.

Однако к сожалению, даже на хабре, об этой технологии рассказывают супер‑поверхностно — как скачать какую‑то GUI программу, и куда тыкать кнопочки. Поэтому я решил исправить это недоразумение, и выпустить первую статьи на русском, где полностью рассказывается что по настоящему стоит за этими 4-мя буквами.

Для прочтении статьи, вам потребуются базовое понимание ML, знание того, что такое полносвязный (dense) слой, умения умножать матрицы и знание того, что такое их ранг.

Дообучение моделей

Продвинутые ML‑щики могут пропускать этот абзац.

При предварительном обучении нейронная сеть изучает общие паттерны и закономерности на большом количестве данных. Этот этап можно сравнить с получением базового образования, которое предоставляет учащемуся знания и навыки, применимые к широкому кругу задач. Однако для решения более специализированных проблем требуется дообучение.

Дообучение представляет собой процесс адаптации обученной нейронной сети к новой, более узкой задаче. Вместо того чтобы обучать модель «с нуля», дообучение позволяет использовать уже полученные знания и наработки, значительно сокращая время и ресурсы, необходимые для обучения. При дообучении модель обучается на новых данных, связанных с конкретной задачей, и оптимизирует свои параметры, чтобы лучше справляться с ней.

Примером может служить нейронная сеть, изначально обученная определять наличие каких то объектов на фотографии. Мы можем дообучить её (то есть изменить ее веса), что бы она теперь умела распознавать другие объекты. При этом дообучить модель сильно проще чем обучать с нуля. Например в данном примере у нейросети уже есть натренированные начальные слои, которые извлекают из изображений низкоуровневые фичи, которые есть во всех типах объектов, и требуемое количество шагов обучения (как и требование к размеру датасета) будет сильно ниже.

Проблемы дообучения больших моделей

Современные модели становятся все больше и больше, вместе с тем растут и требования к железу. Модель GPT-3 и подобные невозможно было бы даже запустить на компьютере с современной массовой видеокартой, не говоря уже об обучении, где помимо прямого прохода, нужно делать и обратный, рассчитывая градиенты по всем параметрам. Таким образом придумать методы эффективного обучения больших моделей это довольно насущная задача. В последнее время было предложено множество подходов, однако все они (кроме лоры) имеют проблемы с задержкой вывода, понижением точности, большой требовательности к дисковому пространству итп.

LoRA

Давайте спустимся на самый простой уровень. У нас есть один линейный слой без функции активации.

Если на вход мы подадим x, на выходе получим где W — матрица весов.

Мы хотим немного изменить принцип работы этого слоя, дообучив модель, скорректировав веса на (которые обычно ищут обычным градиентным спуском), так что бы новый выход был.

Как мы видим, новый отличается от старого на , что можно интерпретировать как результат работы еще одного, отдельного, полносвязного слоя.

Таким образом, мы можем зафиксировать веса матрицы W, а вместо этого учить  — модель предсказывающую отличие результата обычной модели, от дообученой. Это отдаленно напоминает градиентный бустинг, где мы учим каждое следующее решающее дерево исправлять ошибки прошлого.

У читателя, помнящего линейную алгебру с далекого первого курса сразу возникнет вопрос — а где тут выигрыш? Ведь размеры матриц и должны быть одинаковыми, так что в них одинаковое количество обучаемых параметров, и никакого выигрыша в этом нет.

Вот тут и включается в игру слова Low Rank — матрицу маленького ранга можно представить как произведение двух меньшей размерности. Наша матрица может быть размером 100 на 70, но ранг, то есть количество линейно независимых строк или столбцов (если совсем нестрого — таких столбцов которые действительно содержат новую информацию о модели, а не действуют на вектор параметров аналогично соседям ) может быть меньше чем 70 — например 4 или 20.

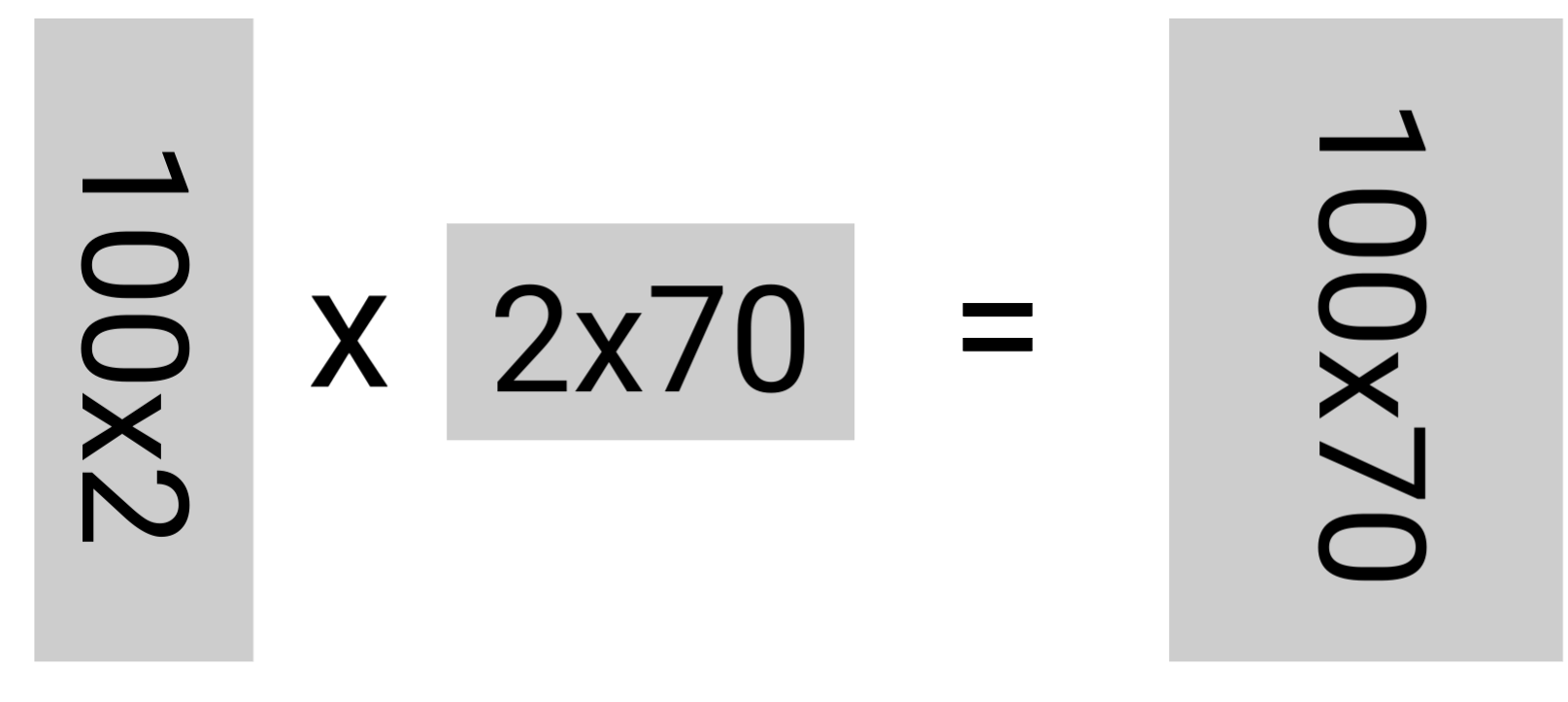
Мы можем представить матрицу как произведение двух матриц A и B, при это сильно выиграем в количестве обучаемых параметров (для примера на картинке, матрица 100 х 70 содержит 7000 чисел, а две в левой части неравенства 140 + 200 = 340, в общем случае потребуется обучать в меньше параметров. r выбирается маленьким порядка 2-8, что делает этот значение очень маленьким ), однако немного потеряем в общности, так как теперь, мы автоматический постулируем что у низкий ранг.

Однако в этом нет ничего страшного, разработчики LoRA ссылаясь на [2] и [3] утверждают что "внутренняя размерность" (intrinsic rank) больших текстовых моделей очень низкая, и большинство параметров, проще говоря, "не работают".
Таким образом, во время обучения нам необходимо хранить в памяти веса W исходной модели и дообучаемой, а считать градиенты только для "новых" маленьких матриц А и В.

При инициализации модели мы создаем матрицу B случайным образом (например из , а матрицу А инициализируем нулями, что бы изначально

Плюсы этого подхода

• Значительно менее ресурсозатратное дообучение. Теперь модель уровня LLaMA / GPT-3* / .... может дообучить под свои задачи, может любой обладатель массовой видеокарты или вообще с использованием google colab, с телефона))).

• Снижение числа обучаемых параметров понижают требования к датасету.

• LoRA модели занимают значительно меньше места на диске. Мы хранить одну "базовую" модель, которая действительно весит много, и большое количество LoRA-модулей (например стилей для Stable Diffusion или дообучений под разные языки для Copilot), которые почти ничего не весят. Из за этого такие модели проще хранить и распространять. Для GPT-3, с 350 ГБ весами, матрицы А и В для всех линейных слоев суммарно занимали 35 Мб!

• Отсутствие задержки вывода. Перед использованием мы можем рассчитать , таким образом новая модель будет требовать столько же вычислений, как и модель без файнтюна.

• Можно менять матрицы А и В прямо налету, посреди диалога, спрашивая у пользователя, например, в каком стиле ему ответить.

QLoRA и Квантование модели

Если этого нам мало, мы можем использовать квантование модели - снижение точности представления весов - например изменяя представление весов с float32->int4 . Эта конвертация имеет значительные преимущества в производительности модели, которые могут перевесить потерю точности.

• float32 представляет примерно 4 миллиарда чисел в интервале ~ [-3.4 , 3.4 ] (да, в компьютерах float-ы занимают только дискретные позиции)

• int8 представляет ~256 чисел вокруг 0.

Казалось бы, такое представление было бы жутко неточным, ведь расстояние между соседними числами было бы

Основная идея данного метода, заключается в том, что несмотря на то, что float32, покрывает огромный диапазон значений, бОльшая часть весов в нейросетях лежат около 0. Таким образом мы выделяем больше "уровней" ближе к началу координат, и меньше вдалеке.

Чуть более научно рассказывается каок это работает в этой статье.

FAQ

1. Если внутренний ранг модели низкий, почему мы не можем представить исходные матрицы W как произведение BA Во первых поиск такого разложения не самая тривиальная задача. Во вторых "внутренний ранг" мал эвристический. Например у матрицы

"Математический" ранг равен 2, но на самом деле, верхняя строчка практический идентична нижней. На вектора она действует аналогично такой матрице.

То есть , но при этом стогого равенства нет!

3) Задавайте вопросы в коментарии или в ЛС, и этот список будет ими дополнятся.

Если эта тема покажется жителям хабра интересной, в следующей статьи я напишу собственную реализацию лоры, а затем попытаемся с ее помощью обучить Open LLaMA разговаривать на русском, переведя весь датасет Alpaca-cleaned и скормив ей для обучения.

Источники

1. LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS

2. Measuring the Intrinsic Dimension of Objective Landscapes

3. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning