Введение

Всем здравствуйте! Иногда у меня возникает потребность в анимированных графиках. Они помогают сделать подачу информации красивее и, что самое главное, нагляднее. Matlab позволяет создавать такие графики, причём с помощью всего нескольких функций. В данной статье будут рассмотрены основные принципы создания анимации — мы сделаем парочку графиков и сохраним всё это в GIF-файлы. Вот один из примеров, чтобы вы понимали, какой можно получить результат:

Как получить кадр и куда-нибудь его записать?

Я думаю, что ни для кого не секрет, что анимация — это последовательность кадров. Чем больше кадров отображается за секунду, тем более плавной нам кажется картинка. Для получения кадра в Matlab есть функция getframe. На кадре может быть только сам график, а может быть и всё графическое окно. Пока что просто построим график привычным нам способом:

x = 0 : 0.01 : 3;
y = 2*x.^3 - 2*sin(tan(x)) + 25*cos(x.^-3);
fh = figure;
plot(x, y)
grid on

Получим кадр всего графического окна и запишем его в JPEG-файл:

frame = getframe(fh);
image = frame2im(frame);
[X, cmap] = rgb2ind(image, 256);
imwrite(X, cmap, 'myframe.jpeg', 'jpeg');

Разберёмся, что происходит в этом коде. С помощью первой строки мы получили кадр. На второй строке мы конвертировали его в картинку с помощью функции frame2im. На третьей строке мы получили индексированное изображение X и его палитру cmap с помощью функции rgb2ind. При этом можно задать, сколько максимум цветов будет в изображении (с помощью второго аргумента функции rgb2ind) — мне кажется, что 256 хватит для любого графика. На четвёртой строке мы используем полученные данные и функцию imwrite, чтобы записать наш график в файл myframe.jpeg. Поменяем первую строку таким образом, чтобы получить график без графического окна:

frame = getframe(gca);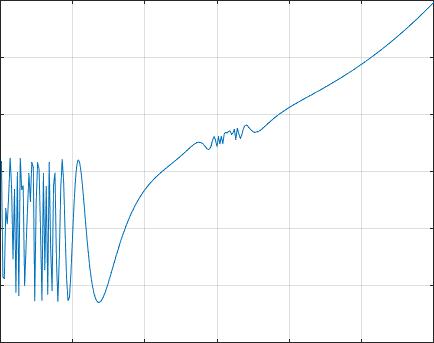

Заметим, что можно идентичный результат можно было получить и с помощью кода ниже:

frame = getframe;

Если у вас несколько графиков и вы хотите получить кадр каких-то конкретных осей, то использовать нужно, разумеется, предыдущий вариант, передавая в функцию getframe интересующие вас оси (с окнами, естественно, работает та же логика).

Попробуем создать первый анимированный график

Давайте сделаем так, чтобы синусоида вечно двигалась вправо:

x = 0 : 0.01 : 2;

for i = 0 : 0.1 : 2
    plot(x, sin(2*pi*x - pi*i))
    xlim([0 2])
    frame = getframe;
    image = frame2im(frame);
    [X, cmap] = rgb2ind(image, 256);
    if i == 0
        imwrite(X, cmap, 'myanim.gif', 'gif', 'LoopCount', Inf, ...
            'DelayTime', 1/24);
    else
        imwrite(X, cmap, 'myanim.gif', 'gif', 'WriteMode', 'append', ...
            'DelayTime', 1/24);
    end
end

Тут я, конечно, воспользовался тем фактом, что сдвиг синусоиды по фазе на два пи равносилен отсутствию её сдвига. Мы плавно повышаем сдвиг фазы от нуля до двух пи, после чего анимация начинается заново (хоть нам и кажется, что она продолжается).

В цикле for на каждой итерации мы получаем новый кадр, после чего сразу записываем его в GIF-файл. Отдельное внимание уделим строкам 9-14 листинга. По умолчанию функция imwrite записывает кадр поверх всего файла, то есть если не менять никакие параметры, на выходе мы получим GIF-файл с одним кадром (последним). При добавлении первого кадра мы ждём именно такого поведения функции, поэтому параметр WriteMode мы не трогаем. С помощью параметра LoopCount мы устанавливаем количество повторений анимации (в данном случае — бесконечное), а с помощью параметра DelayTime — длину кадра (в данном случае это , т.к. желаемая частота кадров анимации — 24 кадра в секунду). Все остальные кадры должны записываться в конец файла, для этого мы изменяем параметр WriteMode на 'append'. Изменяя шаг для переменной i и длину кадра можно менять скорость и плавность анимации.

Создание анимированной линии

Теперь попробуем сделать так, чтобы синусоида рисовалась постепенно (слева направо). Конечно, можно сначала рассчитать вектор со всеми значениями функции, а потом в цикле for постепенно его отрисовывать — сначала только первый элемент, потом первые два элемента, потом первые три и т.д., пока не выведем весь вектор. Этот вариант, конечно, сработает, но в Matlab есть функции animatedline и addpoints, которые можно использовать в подобных ситуациях. Перейдём к примеру:

lh = animatedline;

for i = 0 : 0.01 : 2
    addpoints(lh, i, sin(2*pi*1*i));
    xlim([0 2])
    ylim([-1 1])
    frame = getframe;
    image = frame2im(frame);
    [X, cmap] = rgb2ind(image, 256);
    if i == 0
        imwrite(X, cmap, 'myanim.gif', 'gif', 'LoopCount', Inf, ...
            'DelayTime', 1/60);
    else
        imwrite(X, cmap, 'myanim.gif', 'gif', 'WriteMode', 'append', ...
            'DelayTime', 1/60);
    end
end

На первой строке мы создаём объект анимированной линии. В цикле мы добавляем к нашей линии по одной точке с помощью функции addpoints. Первым аргументом передаём объект анимированной линии, вторым и третьим аргументами — координаты x и y новой точки соответственно. Удалить все точки из объекта анимированной линии можно с помощью функции clearpoints. Получить все его точки можно с помощью функции getpoints.

Пример 1

В начале статьи я приводил пример анимированного графика. Попробуем его, наконец, реализовать:

%% Плавное появление синусоиды

fileName = 'habr1.gif';
figure('Position', [0, 0, 1280, 720])
grid on
sine = animatedline;
sine.Color = 'blue';

f = 1; %Частота синусоиды
for i = 0 : 0.01 : 1
    addpoints(sine, i, sin(2*pi*f*i - pi/12));
    xlim([0, 1])
    ylim([-1.1, 1.1])
    [A, map] = GetIndImage;
    if i == 0
        imwrite(A, map, fileName, 'gif', 'LoopCount', Inf, ...
            'DelayTime', 1/60);
    else
        imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', ...
            'DelayTime', 1/60);
    end
end

%% Раздвоение и сдвиг синусоиды

[sine_x, sine_y] = getpoints(sine);
x = 0 : 0.01 : 1;

for phi = 0 : 0.02 : pi/2
    sine_offset_y = sin(2*pi*f*x - pi/12 - phi);
    hAx = plot(sine_x, sine_y, 'r', ...
        x, sine_offset_y, 'b');
    grid on
    box off
    xlim([0, 1])
    ylim([-1.1 1.1])
    [A, map] = GetIndImage;
    imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', 'DelayTime', 1/60);
end

%% Плавное появление вертикальных линий

left_line = animatedline;
right_line = animatedline;

for i = 1.1 : -0.05 : -1.1
    addpoints(left_line, 1/24, i);
    addpoints(right_line, 0.4166, i);
    xlim([0, 1])
    ylim([-1.1, 1.1])
    [A, map] = GetIndImage;
    imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', 'DelayTime', 1/60);
end

%% Плавное закрашивание области

rh = rectangle('Position', [1/24 -1.2 0.4166-1/24 2.4], 'FaceColor', [0 0 0 0]);

for i = 0 : 0.01 : 0.3
    rh.FaceColor = [0 0 0 i];
    [A, map] = GetIndImage;
    imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', 'DelayTime', 1/60);
end

imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', 'DelayTime', 1.5);

%% Функция получения индексированного изображения

function [A, map] = GetIndImage
    frame = getframe;
    image = frame2im(frame);
    [A, map] = rgb2ind(image, 256);
end

Сразу обращу внимание, что получение индексированного изображения из кадра я вынес в отдельную функцию, её определение на строках 69-73. До 22 строки всё, как мне кажется, должно быть понятно — это плавное появление синусоиды, которое мы делали и в предыдущем разделе. На строке 26 происходит преобразование получившейся синусоиды в набор точек, который потом используется для построения этой же синусоиды с помощью функции plot в следующем цикле. С плавным появлением вертикальных линий, как мне кажется, тоже всё должно быть понятно. Плавное закрашивание области реализовано с помощью плавного понижения прозрачности прямоугольника. Делать так можно, кстати, далеко не со всеми объектами. К сожалению, менять прозрачность текста нельзя. Строка 65 нужна для задержки кадра в конце анимации. То есть на протяжении анимации частота обновления кадров может быть разной.

Пример 2

Напоследок приведу анимацию, которая реально помогает нагляднее представить информацию. Она показывает, что такое эффект "растекания спектра", который возникает при применении дискретного преобразования Фурье.

fileName = 'habr2.gif';
fh = figure('Position', [0 0 1280 720]);
x = -0.1 : 0.01 : 1.5;
y = sin(2*pi*1*x);
counter = 0;

%% Движение вправо

for i = 0.8 : 0.01 : 1.2
    subplot(2, 1, 1)
    plot(x, y, 'LineWidth', 1.5)
    grid on
    rectangle('Position', [0 -1.2 i 2.4], ...
        'FaceColor', [204/255 153/255 255/255 0.3], ...
        'LineWidth', 0.01)
    xline(1, 'r--', 'LineWidth', 1.3)
    xlim([-0.01 1.21])
    ylim([-1.1 1.1])

    subplot(2, 1, 2)
    stem(abs(fft(y(11 : 90 + counter))))
    xlim([0, 121])
    ylim([0, 60])
    counter = counter + 1;
    
    frame = getframe(fh);
    image = frame2im(frame);
    [A, map] = rgb2ind(image, 256);
    if i == 0.8
        imwrite(A, map, fileName, 'gif', 'LoopCount', Inf, 'DelayTime', 1/24);
    else
        imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', 'DelayTime', 1/15);
    end
end

%% Движение влево

counter = counter - 1;
for i = 1.2 : -0.01 : 0.8
    subplot(2, 1, 1)
    plot(x, y, 'LineWidth', 1.5)
    grid on
    rectangle('Position', [0 -1.2 i 2.4], ...
        'FaceColor', [204/255 153/255 255/255 0.3], ...
        'LineWidth', 0.01)
    xline(1, 'r--', 'LineWidth', 1.3)
    xlim([-0.01 1.21])
    ylim([-1.1 1.1])
    
    subplot(2, 1, 2)
    stem(abs(fft(y(11 : 90 + counter))))
    xlim([0, 121])
    ylim([0, 60])
    counter = counter - 1;
    
    frame = getframe(fh);
    image = frame2im(frame);
    [A, map] = rgb2ind(image, 256);
    imwrite(A, map, fileName, 'gif', 'WriteMode', 'append', 'DelayTime', 1/15);
end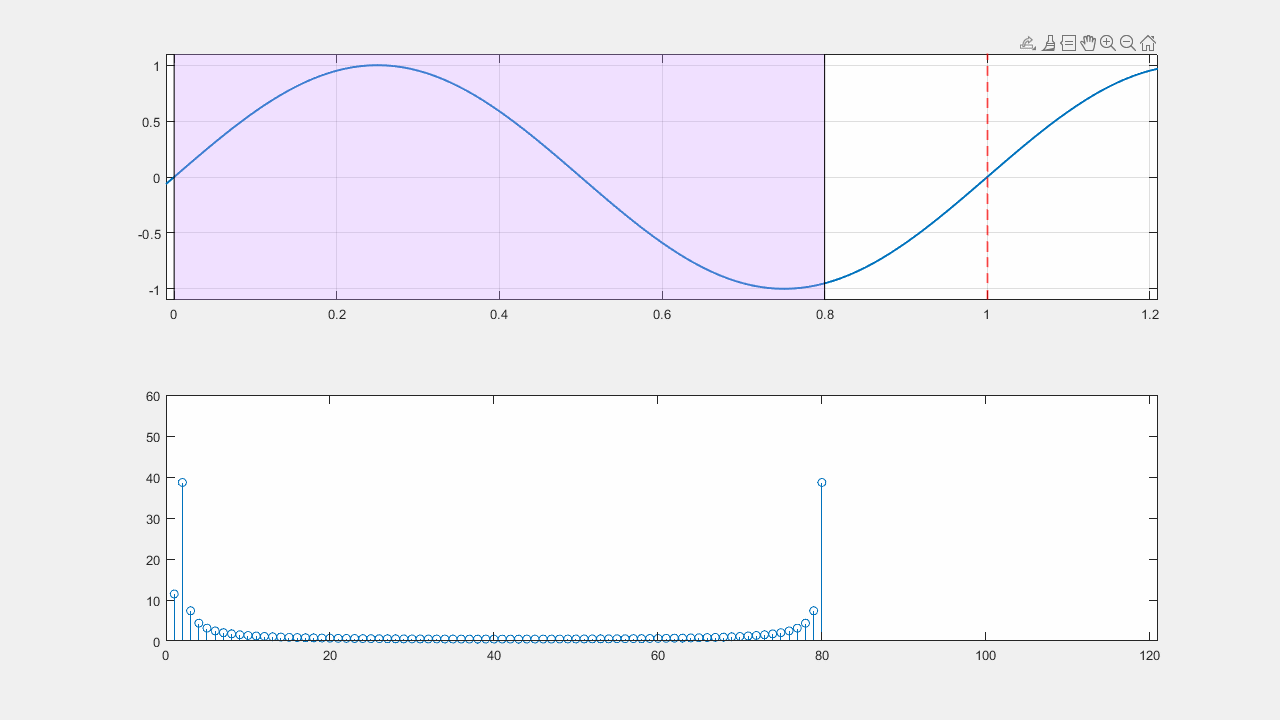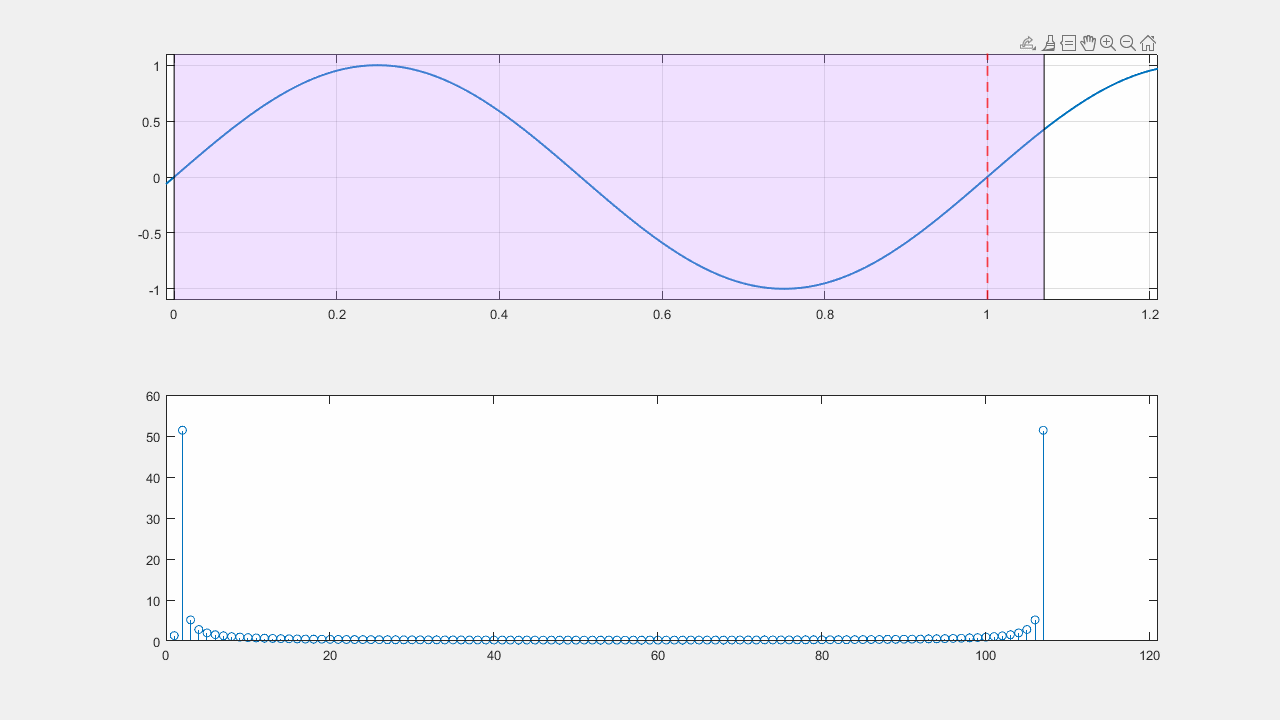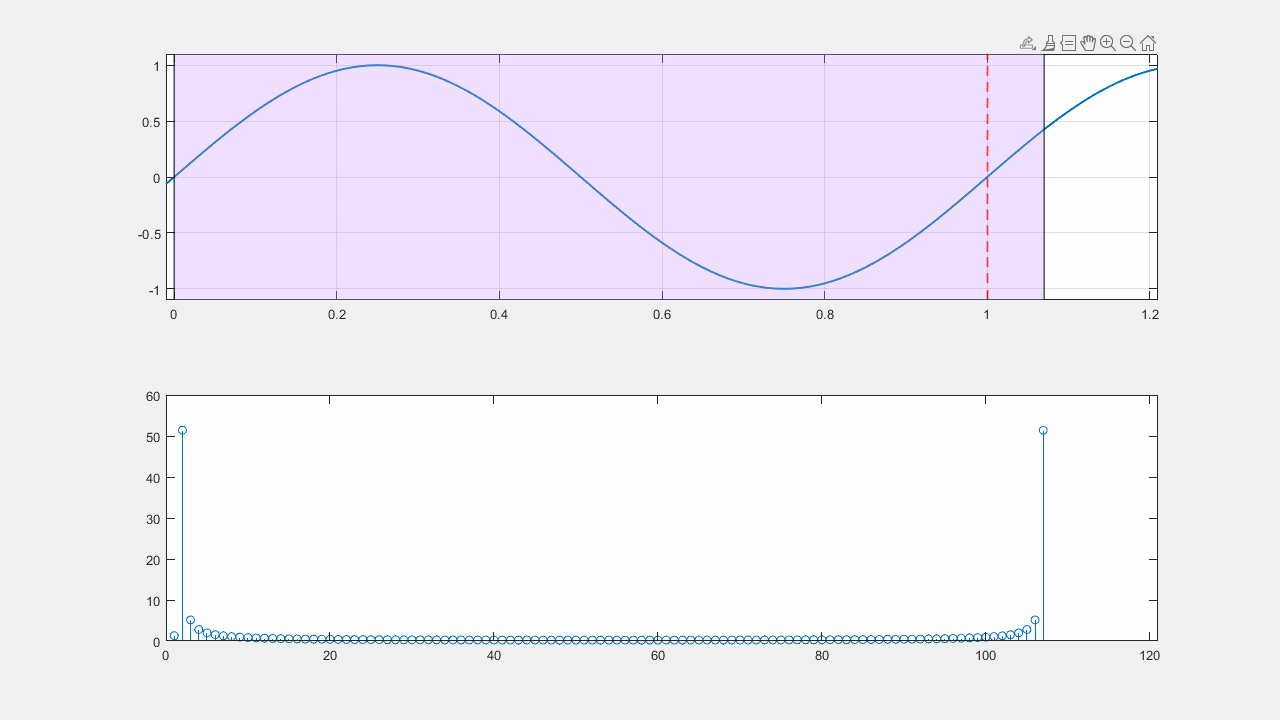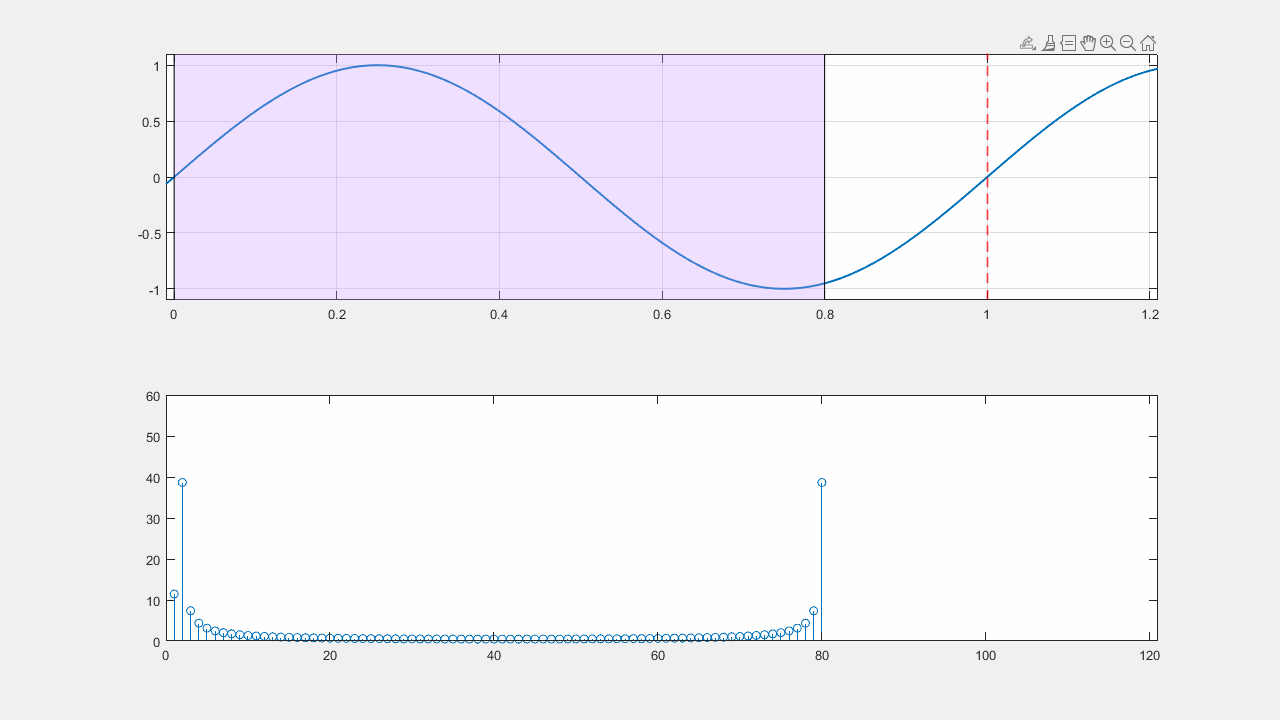

Все приёмы, что есть в приведённом выше коде, мы с вами уже обсудили. Надеюсь, что статья была для вас полезной!