Привет, Хабр!
Должно быть, всем уже известно, что в Smart Engines мы, в частности, занимаемся разработкой томографического программного обеспечения. Чтобы заглянуть внутрь окружающих нас вещей и увидеть чуть больше и чуть точнее, чем дозволено человеческому глазу, мы работаем над совершенствованием алгоритмов реконструкции внутренней структуры объектов. Путь восстановления внутренности объекта тернист: часто томограф, на котором производятся измерения, неидеален, и получаемое изображение внутренности объекта имеет очевидные искажения, двоения, размытия – так называемые артефакты реконструкции объекта. Обнаруженные артефакты реконструкции мешают исследователю в изучении внутренности объекта, их наличие иногда "толкает" исследователя на неверные умозаключения.

В связи с этим с артефактами реконструкции нужно бороться. В зоопарке артефактов томографической реконструкции в особом вольере обитают артефакты, возникающие от неверного определения положения оси, вокруг которой вращается объект в процессе сканирования или же вокруг которой обращается источник излучения, если объект неподвижен. Так что же это за звери такие — артефакты оси вращения? Об этих сущностях и методах их укрощения и пойдет речь в нашей сегодняшней статье.
Введение и постановка задачи
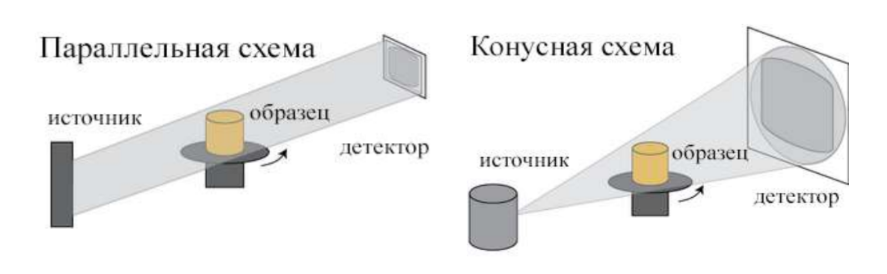
Напомним, что рентгеновская компьютерная томография – метод неразрушающего послойного исследования внутреннего строения объекта по его снимкам в рентгеновском диапазоне. Процесс сбора проекционных данных объекта осуществляется на томографе: объект исследования вращается вокруг некоторой оси вращения с заданным угловым шагом, или же источник излучения движется по некоторой траектории вокруг неподвижного объекта, при этом объект просвечивается рентгеновским излучением. Рентгеновские лучи, пройдя через специальный оптический элемент, могут распространяться параллельно друг другу (параллельная модель распространения рентгеновских лучей) или же могут исходить из точечного источника рентгеновского излучения (конусная модель распространения рентгеновских лучей) (см. рис. 2). Позиционно-чувствительный детектор регистрирует рентгеновские проекционные снимки объекта. Применяя к которым алгоритмы реконструкции, мы можем получить изображение внутренности объекта. С помощью компьютерной томографии инженер может увидеть, например, качественно ли изготовлена та или иная деталь промышленного оборудования, а медик может выяснить, нет ли у обследуемого пациента повреждений внутренних органов.
Положение оси вращения объекта выступает одним из главных героев в описанной схеме сбора проекционных данных. Оно является крайне важным параметром классических алгоритмов томографической реконструкции. Из-за использования неточно определенного расположения оси вращения на границах реконструированных слоев томографированного объекта возникают артефакты в виде полосоподобных искажений, раздвоений и размытий (полосоподобные артефакты типа камертона, tuning fork artifacts) (рис. 3).

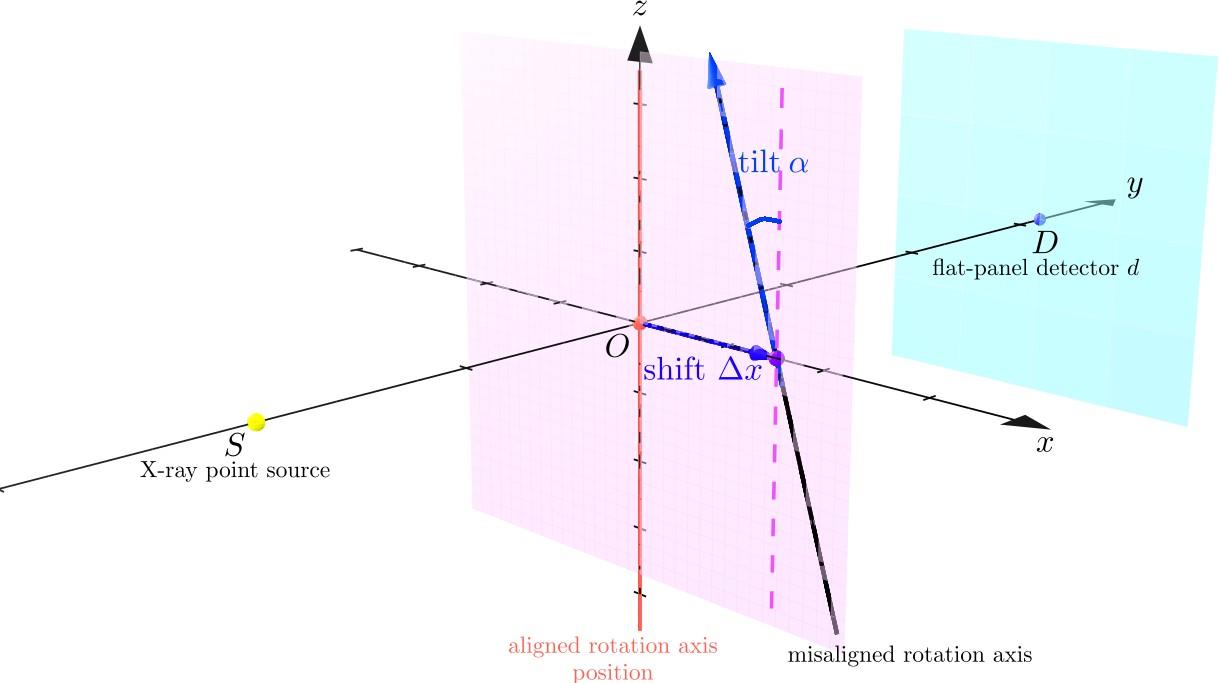
При этом в рентгеновской компьютерной томографии ось вращения объекта нередко наклоняется и смещается от своего идеального вертикального положения ввиду большой скорости вращения составных частей томографа - гантри или гониометра. Ось может претерпеть как сдвиги, так и наклоны в разных плоскостях: на рисунке 4 изображена модель оси вращения, в рамках которой допускаются сдвиги в горизонтальной плоскости вдоль окна детектора и наклоны в плоскости, параллельной плоскости окна детектора. Поэтому в условиях отклонения оси вращения объекта от идеального выровненного положения для получения высококачественной реконструкции внутренней структуры объекта требуется либо предварительная калибровка томографической установки, которая не всегда возможна, либо автокоррекция положения оси вращения с помощью измеренных данных.
Методы поиска оси вращения в компьютерной томографии
Как же можно найти истинное положение оси вращения в томографическом эксперименте? Разумеется, самые первые методы калибровки оси заключались в томографировании специальных тестовых модельных объектов - фантомов. Фантомы, предназначенные для калибровки оси и детектора, часто имеют вид столбчатых или сетчатых структур. Надежный сообщник в расследовании дела уклонившейся оси вращения - квадратная решетка; она может показать, как и насколько далеко ось "убежала" от вертикального положения в ходе сканирования. Специальные фантомы сконструированы таким образом, что по их проекционным снимкам можно легко обнаружить след сместившейся оси и определить ее актуальное положение в пространстве. Например, говоря о столбчатом или решетчатом фантоме, величина сдвига оси вращения в плоскости, параллельной плоскости окна детектора, равна расстоянию от проекции ребер решетки или столбцов фантома до центра соответствующего проекционного снимка. В то же время о наклонах оси вращения в плоскости, параллельной плоскости окна детектора, говорит расположение проекций цилиндрических столбцов фантома и ребер решетки на проекционных снимках под ненулевым углом к вертикальному направлению.

Не новы методы, основанные на использовании в томографическом эксперименте эталонных маркеров (фидуциарных маркеров): эти методы предполагают отслеживание траектории таких маркеров, как маленькие золотые бусины или шарики из кремнезема, которые либо устанавливаются в контейнере для образца (например, капилляре), либо непосредственно помещаются в или на образец. Положение маркеров определяется по относительному расположению и динамике областей высокой контрастности на проекционных снимках.
Несмотря на высокую точность, маркерный метод имеет существенным недостатком большие затраты на более сложную подготовку образцов. Предварительная калибровка положения оси вращения и детектора посредством сканирования вспомогательного фантома замедляет изучение структуры целевого объекта. Маркеры также создают дополнительную плотность в 3D-реконструкции, которая приводит к появлению артефактов и которую дополнительно необходимо отфильтровать для последующего корректного анализа внутренней структуры исходного образца.
На пути совершенствования методов поиска положения оси вращения после методов калибровки оси и детектора с помощью проекционных данных специальных фантомов или объекта, нагруженного референсными маркер-вставками, естественно возникли методы автоматического определения параметров положения оси вращения. Они не требуют дополнительных измерений исследователя и изменений исследуемого образца.
Время не стоит на месте, и сегодня против преступности в лице уклоняющихся осей вращения подготовлен целый спецназ классических методов определения положения оси вращения, которые могут быть условно разделены на 4 группы методов, основанных на
i. сравнении проекций объекта, которые отвечают отличающимся на 180 градусов углам поворота объекта (методы кросс-корреляции и фазовой корреляции) [1 – 5];
ii. построении траектории движения точки центра масс проекционного снимка или некоторой другой выделенной точки на проекции при изменении угла поворота объекта [6, 7];
iii. экстремизации определенных функций реконструкции [8, 9];
iv. многократном репроецировании объекта [10].
Вероятно, первыми в истории методами автоматического определения параметров положения оси вращения стали методы, основанные на сравнении проекционных снимков объекта, отвечающих отличающимся на 180 градусов углам проецирования (i). В рамках группы методов (i) предполагается, что проекционные снимки, отвечающие противоположным углам поворота объекта, получаются друг из друга отображением проекции относительно оси вращения на плоскость окна детектора (при условии неподвижности источника рентгеновского излучения при обращении объекта вокруг оси). Другими словами, если наклонов и сдвигов оси нет, проекции объекта "лицом" и "затылком" к исследователю зеркально симметричны относительно срединной вертикали проекционных снимков. Если же ось сдвинута, то рентгеновская "тень" объекта на детекторе будет зеркально симметрична уже относительно не срединной вертикали, а проекции оси вращения на плоскость детектора (рис. 6).

Вектор сдвига оси вращения может быть определен точкой максимума кросс-корреляционной функции проекционного снимка и противоположного к нему зеркально отраженного относительно вертикали снимка, - это так называемый кросс-корреляционный метод [1]. В другом же методе рассматриваемой группы (i), - методе фазовой корреляции [2, 3] (рис. 7), - противоположные проекционные снимки заменяются их фазами. Сдвиг оси определяется положением точки максимума кросс-корреляционной функции фаз проекционного снимка и противоположного к нему зеркально отраженного относительно вертикали снимка. Метод фазовой корреляции позволяет находить не только сдвиг оси, в отличие от метода кросс-корреляции, но и наклон оси в плоскости, параллельной плоскости окна детектора.
![Рис. 7. Метод фазовой корреляции [2, 4] позволяет сопоставлять изображения, полученные преобразованиями сдвига, поворота и масштабирования из одного и того же изображения: изображение (c) иллюстрирует положение изображения (b) на изображении (a) (изображение из работы [2]) Рис. 7. Метод фазовой корреляции [2, 4] позволяет сопоставлять изображения, полученные преобразованиями сдвига, поворота и масштабирования из одного и того же изображения: изображение (c) иллюстрирует положение изображения (b) на изображении (a) (изображение из работы [2])](https://habrastorage.org/getpro/habr/upload_files/313/42a/047/31342a0479d1f0276997e8ac4eb3cdaa.png)
Методы группы (i) представляются вычислительно трудоемкими, так как для определения положения оси с высокой точностью требуют рассмотрения не одной пары противоположных проекций, для каждой из которой посредством, как правило, вычислений не менее трех двумерных быстрых дискретных преобразований Фурье определяется функция корреляции между снимками проекций или их фазовая корреляция. Другой недостаток методов группы заключается в необходимости использования в точности противоположных проекций: результаты методов на приближенно противоположных проекциях могут иметь существенную ошибку. Вдобавок методы группы (i) точны при использовании модели параллельного распространения рентгеновских лучей. Применение методов в конусной модели не всегда обеспечивает достаточно точного приближения истинных значений параметров положения оси вращения.
Ключевое наблюдение, лежащее в идейном фундаменте методов другой группы (ii), выражается в том, что проекция выбранной на объекте точки на плоскость детектора движется согласно синусоидальному закону по горизонтали и вертикали при монотонном изменении угла проецирования, тем самым колеблясь около проекции оси на плоскость детектора (рис. 8). Параметры положения оси вращения подбираются из принципа аппроксимации траекторией движения выбранной точки гармоники. Ввиду обработки всего массива измеренных данных методы (ii) относительно медленны. Будучи сфокусированными на точечных особенностях проекций, они менее устойчивы к шуму в измеренных данных, чем методы группы (i).
![Рис. 8. Методы второй группы реконструируют эллиптическую траекторию движения проекции выбранной точки объекта на плоскость окна детектора. Параметры положения оси вращения описывают геометрические параметры эллипса [7]. Рис. 8. Методы второй группы реконструируют эллиптическую траекторию движения проекции выбранной точки объекта на плоскость окна детектора. Параметры положения оси вращения описывают геометрические параметры эллипса [7].](https://habrastorage.org/getpro/habr/upload_files/3a4/6d5/865/3a46d58655e9874388a670874a1339c0.png)
В рамках группы методов (iii) параметры положения оси вращения подбираются из принципа максимизации определенных функций реконструированного объема. Предлагаются самые разные эвристики: например, максимизация количества пикселей ненулевой интенсивности в реконструированном слое, максимизация контрастности изображения реконструированного слоя или минимизация полной вариации реконструированного объема объекта. Отметим, что на каждой итерации методов (iii), при каждом пробном наборе значений параметров положения оси вращения требуется реконструирование отдельного слоя объекта или же всего его объема, что может иногда занять часы, если не дни…
Авторы методов группы (iv) предлагают многократно производить репроецирование текущего реконструированного объема, служащего приближением к искомой идеальной реконструкции внутренней структуры объекта, при различных пробных параметрах положения оси вращения и считать истинными параметрами положения оси вращения такие, при которых полученные репроецированием проекции максимально совпадают с имеющимися исходными проекционными данными. Иначе говоря, берем начальное приближение к целевой реконструкции и проецируем ее (применяем к ней оператор прямого проецирования). Если результат прямого проецирования сильно разнится с измеренными проекционными данными в эксперименте, немного изменим, возмутим реконструкцию и параметры положения оси вращения и снова спроецируем реконструкцию - уже с измененным предполагаемым положением оси. Если вновь попали “мимо” исходно измеренных проекций, возмущаем ось и реконструкцию еще раз. И так до того момента, пока полученные после возмущения оси и реконструкции репроекции не станут близкими к исходным измерениям.
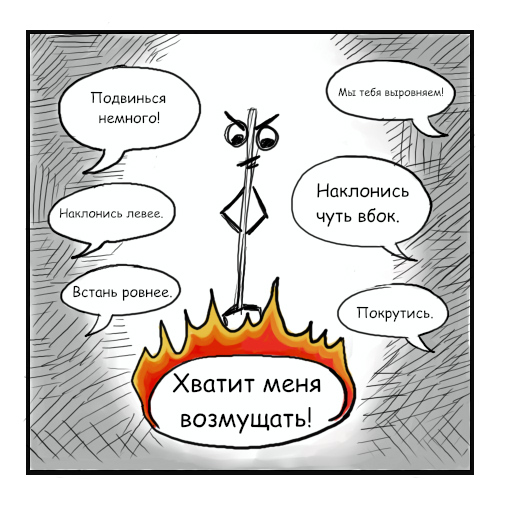
Несмотря на независимость метода (iii) экстремизации определенных функций оценки качества реконструкции и метода (iv) репроецирования от используемой модели распространения рентгеновских лучей, эти методы в различных своих вариациях, как правило, являются вычислительно трудоемкими и довольно медленными, так как требуют многократного осуществления реконструкции нескольких или всех слоев объекта.
Для полноты изложения следует также упомянуть сегодня активно развивающиеся методы определения положения оси вращения при помощи методов глубокого обучения (например, [11]). Нейросеть на размеченных датасетах обучают находить и оценивать количество артефактов на реконструкции (например, оценивать наличие и степень выраженности артефактов реконструкции в виде колец, или кольцевых артефактов). Параметры положения оси вращения, предлагаемые нейросетью, таковы, что оценка нейросети количества артефактов реконструкции, получаемой при данных параметрах положения оси вращения, минимальна. Нейросетевые методы все-таки нельзя отнести к классическим методам, они еще во многом развиваются, но, возможно, будущее за ними.
Как мы видим, большинство быстрых классических методов автоматического определения положения оси вращения дают удовлетворительно точные для практических целей результаты в рамках круговой схемы сканирования с параллельной моделью распространения рентгеновских лучей. Однако они оказываются непригодными для конусной модели, представляющей на текущий момент наиболее часто используемую модель распространения рентгеновских лучей. Классические методы, безразличные к геометрической схеме, вычислительно трудоемкие и относительно медленные. Методы, анализирующие локальные особенности проекционных снимков и их динамику, неустойчивы у шумам на проекционных данных.
Заключение
Разработка методов автоматического поиска параметров положения оси вращения в компьютерной томографии остается актуальной. Все еще требуются быстрые методы поиска положения оси вращения, одинаково точно работающие в различных моделях распространения рентгеновских лучей, при этом также отличающиеся устойчивостью к шуму в данных. Над разработкой методов поиска оси вращения работает и наш отдел, и, быть может, в скором времени мы расскажем тебе, Хабр, о том, как мы ищем положение оси вращения. А сейчас нам надо срочно успеть за осью: наклонится и убежит - найдем ли мы ее потом?

Будем держать тебя в курсе наших новостей, Хабр!
Список литературы
Frank J., McEwen B. F. Alignment by cross-correlation //Electron tomography: three-dimensional imaging with the transmission electron microscope. – Boston, MA : Springer US, 1992. – С. 205-213.
Reddy B. S., Chatterji B. N. An FFT-based technique for translation, rotation, and scale-invariant image registration //IEEE transactions on image processing. – 1996. – Т. 5. – №. 8. – С. 1266-1271.
Wong A., Orchard J. Robust multimodal registration using local phase-coherence representations //Journal of Signal Processing Systems. – 2009. – Т. 54. – С. 89-100.
Реализация метода определения относительных сдвигов, поворотов и масштабирований изображений, основанного на использовании дискретного преобразования Фурье (на языке программирования python): https://imreg-dft.readthedocs.io/en/latest/index.html.
Vacek E., Jacobsen C. Fast and noise-tolerant determination of the center of rotation in tomography //Journal of Synchrotron Radiation. – 2022. – Т. 29. – №. 2. – С. 488-495.
Guizar-Sicairos M. et al. Phase tomography from x-ray coherent diffractive imaging projections //Optics express. – 2011. – Т. 19. – №. 22. – С. 21345-21357.
Ferrucci M. et al. Towards geometrical calibration of x-ray computed tomography systems—a review //Measurement Science and Technology. – 2015. – Т. 26. – №. 9. – С. 092003.
Kingston A. et al. Reliable automatic alignment of tomographic projection data by passive auto‐focus //Medical physics. – 2011. – Т. 38. – №. 9. – С. 4934-4945.
Varslot T. et al. High‐resolution helical cone‐beam micro‐CT with theoretically‐exact reconstruction from experimental data //Medical physics. – 2011. – Т. 38. – №. 10. – С. 5459-5476.
Pande K. et al. Joint iterative reconstruction and 3D rigid alignment for X-ray tomography //Optics Express. – 2022. – Т. 30. – №. 6. – С. 8898-8916.
Yang X. et al. A convolutional neural network approach to calibrating the rotation axis for X-ray computed tomography //Journal of synchrotron radiation. – 2017. – Т. 24. – №. 2. – С. 469-475

