07.08.2023 09:30
SmartEngines 0 536 Источник

Привет, Хабр!

Как ты помнишь, в Smart Engines мы разрабатываем томографическое программное обеспечение. Иногда в промышленных и медицинских целях важно заглянуть внутрь окружающих нас вещей, чтобы обнаружить глазом не различимые дефекты детали или же предупредить возникновение заболевания определенного внутреннего органа человека. К сожалению, нередко на пути восстановления внутренней структуры объектов мы сталкиваемся с множеством трудностей: томограф, используемый для сбора измерений изучаемого объекта, как правило, неидеален, и получаемое изображение внутренности объекта имеет очевидные искажения, двоения, размытия, на нем видны полосообразные или кольцеобразные элементы повышенной или пониженной интенсивности – так называемые артефакты реконструкции объекта. Такие артефакты реконструированного изображения запутывают исследователя и толкают его в пучину заблуждений.

Артефакты реконструкции имеют самые разные причины происхождения и различаются своим характером проявления на реконструкции, при этом всех их роднит общий умысел - порча качества реконструкции. Существуют артефакты, возникающие из-за смещенного положения оси вращения во время сканирования объекта, - о таких артефактах и методах их коррекции мы рассказывали ранее. Сегодня же мы бы хотели рассказать о других покемонах - о кольцевых артефактах реконструкции и существующих методах их подавления.

Рис. 1. Путь получения высококачественной реконструкции тернист: иногда этому препятствуют кольцевые артефакты на реконструкции.
Рис. 1. Путь получения высококачественной реконструкции тернист: иногда этому препятствуют кольцевые артефакты на реконструкции.

Кольцевые артефакты: что это такое и почему они появляются на реконструкции?

Напомним нашему читателю, что рентгеновская компьютерная томография – метод неразрушающего послойного исследования внутреннего строения объекта по его трансмиссионным (на просвет) снимкам в рентгеновском диапазоне. Ключевой инструмент сбора проекционных данных объекта - томограф. Во время сканирования объект исследования вращается вокруг некоторой оси вращения с заданным угловым шагом, или же источник излучения движется по некоторой траектории вокруг неподвижного объекта, при этом объект просвечивается рентгеновским излучением. Позиционно-чувствительный детектор регистрирует рентгеновские проекционные снимки объекта. Применяя к зарегистрированным проекционным данным алгоритмы реконструкции, исследователь может получить изображение внутренности объекта. 

Процедура сбора проекционных данных объекта невозможна без детектора. При этом детектор на практике далек от идеального регистрирующего устройства: его пиксели могут быть неоткалиброваны, не исключено наличие неработающих, битых пикселей. Неисправности детектора могут стать причиной появления на реконструированном изображении так называемых кольцевых артефактов - артефактов, которые представляют собой концентрические кольцеобразные элементы повышенной или пониженной интенсивности на реконструкции объекта, имеющие общий центр – точку пересечения реконструированного слоя с осью вращения объекта (рис. 2).

Рис. 2. Реконструкция центрального слоя пакета реальных данных плода перца: a) реконструкция с кольцевыми артефактами; б) реконструкция с подавленными кольцевыми артефактами.
Рис. 2. Реконструкция центрального слоя пакета реальных данных плода перца: a) реконструкция с кольцевыми артефактами; б) реконструкция с подавленными кольцевыми артефактами.

Кольцевые артефакты обычно имеют вид либо замкнутых колец (диапазон сканирования - 0°-360°) (рис. 2), либо полуколец (диапазон - 0°-180°) (рис. 3).

Рис. 3. Кольцевые артефакты в диапазоне сканирования 0°-180° [1].
Рис. 3. Кольцевые артефакты в диапазоне сканирования 0°-180° [1].

На изображении синограммы, значения строк которой являются зарегистрированными значениями одной и той же строки детектора при различных углах просвечивания объекта, кольцевые артефакты проявляются в виде полос выделяющейся интенсивности, носящих в литературе название полосовых артефактов (рис. 4). Часто полосы на синограмме едва видны невооруженным глазом, что усложняет задачу определения на синограмме положения полосовых артефактов, которые могут породить на реконструкции кольцевые артефакты.

Рис. 4. Пример синограммы с полосовыми артефактами. Прямоугольными рамками отмечена увеличенная часть синограммы до и после коррекции синограммы. a) Исходная синограмма с полосовыми артефактами, б) Синограмма без полосовых артефактов, в) Абсолютная разность синограмм до и после коррекции.
Рис. 4. Пример синограммы с полосовыми артефактами. Прямоугольными рамками отмечена увеличенная часть синограммы до и после коррекции синограммы. a) Исходная синограмма с полосовыми артефактами, б) Синограмма без полосовых артефактов, в) Абсолютная разность синограмм до и после коррекции.

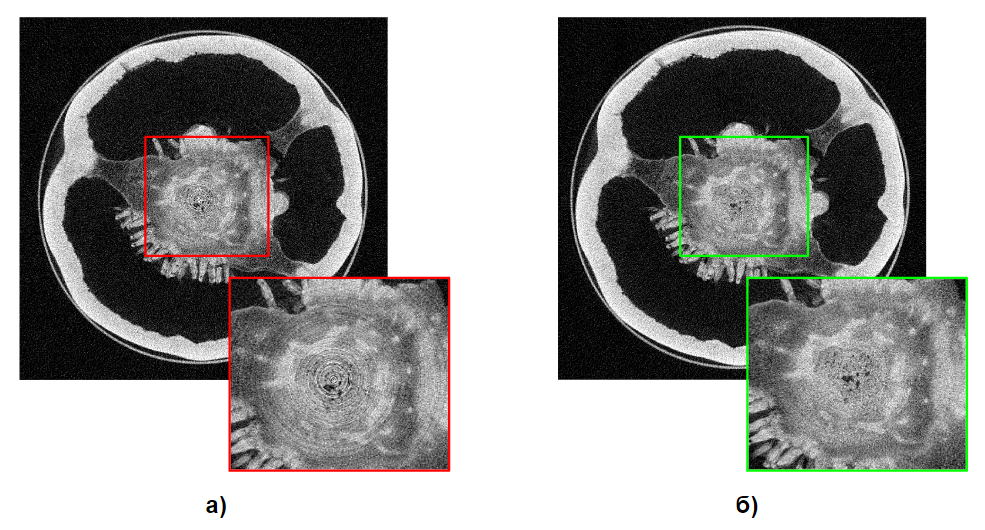
Причины появления на реконструкции кольцевых артефактов многообразны. Во-первых, выделяют естественные причины: ввиду квантовой природы света фотон может быть "пойман" несколькими ячейками детектора. Во-вторых, технические несовершенства детектора, а именно неравномерная чувствительность пикселей детектора (неоткалиброванность пикселей детектора, с этим тесно связано в компьютерной томографии, например, понятие гетероскедастичности, о котором мы уже писали несколько ранее), наличие битых пикселей (отсюда другое название артефактов – “non-uniformity artifacts”) – наиболее распространенная другая причина появления кольцевых артефактов. Битые пиксели вызывают появление сильно выраженных изолированных колец на реконструкции (рис. 5a), в то время как неоткалиброванные ячейки детектора порождают более слабые, широкие кольца или группы колец (известные как “band artifacts”) (рис. 5б и 5в). В-третьих, примеси в сцинтилляционном кристалле или пыль на сцинтилляционных экранах также могут быть причиной сильно выраженных изолированных (как правило, узких) колец на реконструированном изображении.

Рис. 5. a)“Сильные” изолированные кольца. Реконструкция слоя конденсатора. [2], б) Изолированные “слабые” кольца в центральной части реконструированного изображения и группы “слабых” на периферии слоя. Окаменелость с останками птицы [3], в) Группы “слабых” колец. Банан.
Рис. 5. a)“Сильные” изолированные кольца. Реконструкция слоя конденсатора. [2], б) Изолированные “слабые” кольца в центральной части реконструированного изображения и группы “слабых” на периферии слоя. Окаменелость с останками птицы [3], в) Группы “слабых” колец. Банан.

Четвертая причина появления кольцевых артефактов – непостоянство режима работы рентгеновской трубки, непостоянство интенсивности рентгеновского излучения. Для такой причины характерны кольцевые артефакты непостоянной интенсивности (интенсивность неодинакова в различных частях кольца) (рис. 6). Наконец, из-за особенностей исследуемого образца на реконструкции могут также наблюдаться кольцевые артефакты. В частности, на это сказывается наличие в зондируемом объекте областей резкого изменения величины линейного коэффициента ослабления зондирующего излучения.

Рис. 6. Непостоянство интенсивности рентгеновского излучения. Модельные данные (фантом Шеппа-Логана): а) синограмма с полосовыми артефактами; б) реконструированный слой фантома Шеппа-Логана.
Рис. 6. Непостоянство интенсивности рентгеновского излучения. Модельные данные (фантом Шеппа-Логана): а) синограмма с полосовыми артефактами; б) реконструированный слой фантома Шеппа-Логана.

Какова бы ни была причина возникновения кольцевых артефактов на реконструкции, кольцевые артефакты ухудшают качество реконструкции. В связи с этим особо актуальной представляется разработка методов подавления кольцевых артефактов, с использованием которых путем фильтрации проекционных данных или самой реконструкции непосредственно, можно было бы получить реконструированное изображение с менее выраженными кольцевыми артефактами. 

Методы подавления кольцевых артефактов в компьютерной томографии

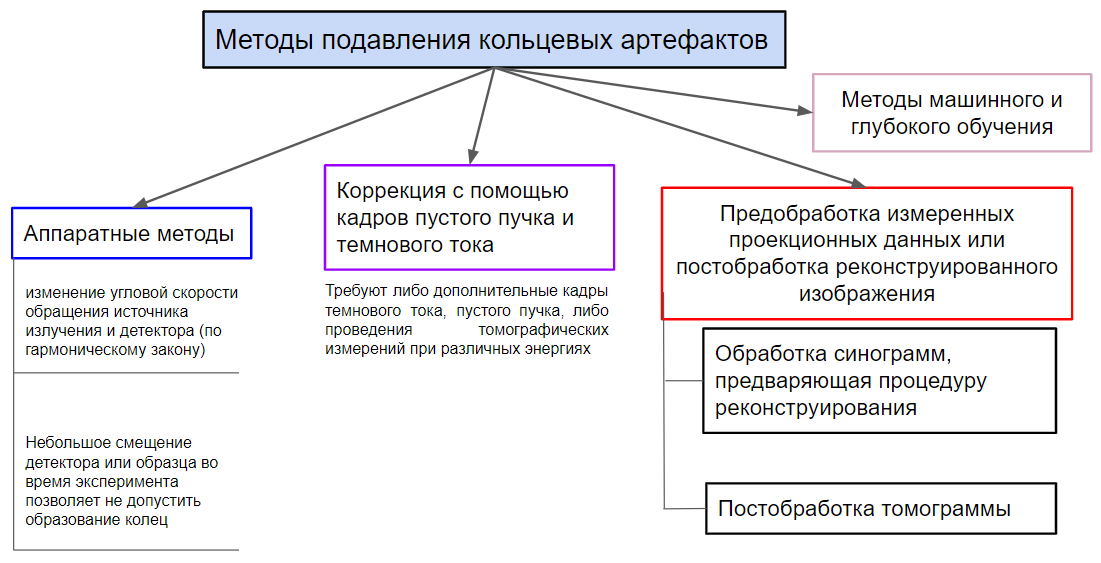
К счастью, к сегодняшнему дню насчитывается большой арсенал методов борьбы с кольцевыми артефактами. Существующие методы можно условно разделить на 4 группы (рис. 7):

  1. Аппаратные методы;

  2. Методы коррекции проекционных данных с помощью кадров пустого пучка и темнового тока;

  3. Методы, основанные на предобработке измеренных проекционных данных или постобработке реконструированного изображения (или во время реконструкции);

  4. Методы машинного и глубокого обучения.

Рис. 7. Классификация методов подавления кольцевых артефактов.
Рис. 7. Классификация методов подавления кольцевых артефактов.

Аппаратные методы подавления кольцевых артефактов подразумевают намеренное изменение параметров измерительной схемы во время сканирования исследуемого образца. В рамках данной группы методов предлагается, например, во время сбора проекционных данных варьировать угловые скорости вращения источника рентгеновского излучения и детектора [4]. Вращение источника рентгеновского излучения с постоянной угловой скоростью при изменении угловой скорости вращения блока детекторов согласно гармоническому закону (такая эволюция скорости движения детектора именуется синусоидальной модуляцией угловой скорости блока детекторов) может уменьшить кольцевые артефакты на реконструкции (рис. 8). Другими словами, в случае, когда детектор движется с осциллирующей угловой скоростью, так, что он колеблется вокруг положения, которое бы он занимал при вращении с постоянной угловой скоростью, удается добиться уменьшения кольцевых артефактов реконструкции.

Рис. 8. Метод синусоидальной модуляции угловой скорости блока детекторов [4]. Во время сканирования угловая скорость блока детектора изменяется согласно гармоническому закону.
Рис. 8. Метод синусоидальной модуляции угловой скорости блока детекторов [4]. Во время сканирования угловая скорость блока детектора изменяется согласно гармоническому закону.

Другой аппаратный метод основан на совершении сдвигов детектора или объекта с определенными горизонтальными шагами во время сбора проекционных данных [5]. При такой организации процедуры сбора проекционных данных объект проецируется на разные области окна детектора после сдвига его оси вращения или самого детектора (рис. 9). Благодаря тому, что индивидуальный пиксель детектора “видит” разные части объекта, подавляется влияние неравномерных откликов детектора.

Рис. 9. Метод сдвига детектора или объекта [5].
Рис. 9. Метод сдвига детектора или объекта [5].

Аппаратные методы дают возможность эффективно подавить кольцевые артефакты, однако при этом требуют сложной подготовки измерительной схемы, которая не всегда возможна. Существенный недостаток первой группы методов – снижение пространственного разрешения реконструкции, если смещения детектора или объекта точно не известны. Приближенно заданные величины сдвигов могут стать причиной появления артефактов оси вращения.

В отдельную группу методов подавления кольцевых артефактов выделяют методы, использующие кадры темнового тока и пустого пучка – изображения отклика детектора в случаях выключенного источника и включенного источника и убранного объекта соответственно. Если I_D – кадр темнового тока, I_B – кадр пустого пучка, {\mu}_D и {\mu}_B – средние значение интенсивности пикселей изображений I_D и I_B (двумерных одноканальных изображений), то линейное преобразование значения интенсивности каждого (x,y) пикселя проекционного снимка I_R, называемое нормировкой, задается формулой

I_C(x,y)=G(x,y) \cdot I_R(x,y)+O(x,y),

где G(x,y)=(\mu_B - \mu_D)/(I_B(x,y)-I_D(x,y)), O(x,y)=\mu_B-G(x,y) \cdot I_B(x,y), I_C – скорректированный при подавлении кольцевых артефактов проекционный снимок, позволяет уменьшить выраженность кольцевых артефактов на реконструкции [6]. Более благоприятной для подавления колец оказывается ситуация, когда доступны не по одному кадру пустого пучка и темнового тока, а по несколько штук (когда кадры пустого пучка сняты при различных значениях интенсивности рентгеновского излучения). В таком случае вместо линейной трансформации значений интенсивности пикселей зарегистрированных проекционных изображений может быть использована кусочно-линейная трансформация. Кусочно-линейная коррекция значения интенсивности фиксированного (x,y) пикселя проекции производится следующим образом: по средним значениям каждого снимка \mu_{0k} и значениям интенсивности выбранного пикселя I_{0k}(x,y) снимков пустого пучка и темнового тока I_{0k} строится кусочно-линейная функция (рис. 10а); при сравнении значения интенсивности выбранного пикселя I_R(x,y) текущего проекционного снимка I_R определяется линейный участок кусочно-линейной функции, то есть коэффициенты G(x,y) и O(x,y), использующиеся для последующей уже описанной нормировки (результат коррекции на 10б).  В качестве обобщения описанного подхода могут быть использованы иные сплайны, проходящие через точки (I_{0k}(x,y),\mu_{0k}). Существенное требование методов, использующих кадры пустого пучка и темнового тока, которое ограничивает их использование, – необходимость наличия кадров пустого пучка и темнового тока. Съемка же кадров занимает дополнительное время исследователя и не всегда доступна.

Рис. 10. Метод кусочно-линейной коррекции проекционных данных по кадрам пустого пучка и темнового тока: a) вид кусочно-линейного преобразования; б) результат коррекции [6].
Рис. 10. Метод кусочно-линейной коррекции проекционных данных по кадрам пустого пучка и темнового тока: a) вид кусочно-линейного преобразования; б) результат коррекции [6].

Группа, вероятно, самых распространенных методов подавления кольцевых артефактов – методы предобработки измеренных проекционных данных или постобработки реконструированного изображения. Если рассматривать методы предобработки проекционных данных, долгое время, до 1970х годов, с кольцевыми артефактами преимущественно боролись путем применения фильтров высоких частот, являющихся модификациями классического Ram-Lak фильтра, на этапе свертки интегральных алгоритмов реконструкции (вариации Ram-Lak фильтра на рис. 11).

Рис. 11. Модификации Ram-Lak фильтра, применяющиеся на этапе свертки интегральных алгоритмов реконструкции [7].
Рис. 11. Модификации Ram-Lak фильтра, применяющиеся на этапе свертки интегральных алгоритмов реконструкции [7].

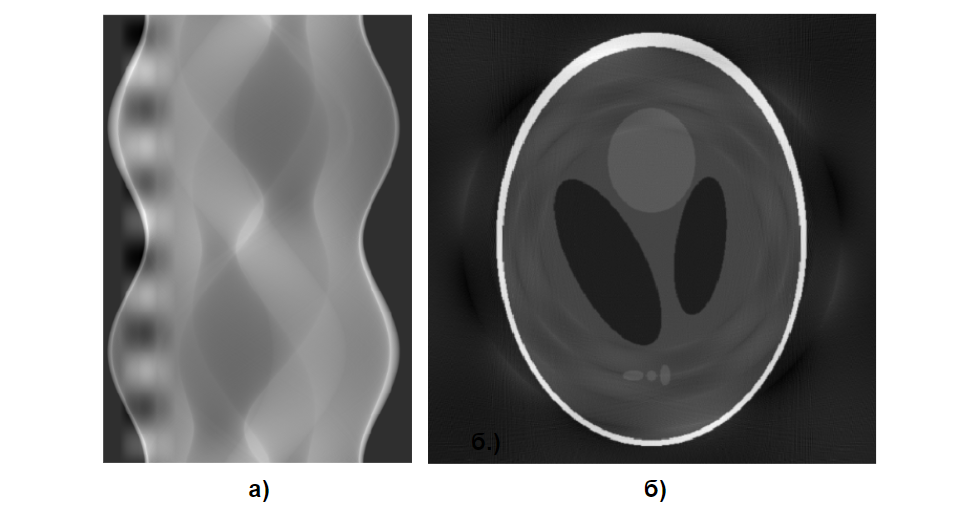
В работах многократно исследовалась способность Hann фильтра [8] и его модификаций [9, 10] подавлять несильно выраженные кольца. При использовании интегральных алгоритмов реконструкции с целью подавления кольцевых артефактов также может быть использована свертка синограммы с фильтром Баттерворта в частотной области [11]. Несмотря на большую вычислительную трудоемкость, фильтр Баттерворта может быть предпочтительнее по сравнению с фильтром с резкой отсечкой частот из-за склонности последнего к появлению шумов из-за медленного убывания функции sinc(x)=\sin(x) /x=O(1/x) (x \rightarrow\infty)в реальном пространстве (результат применения фильтра Баттерворта на рис. 12).

Рис. 12. Синограмма и реконструкция до и после применения коррекции полосовых артефактов [11].
Рис. 12. Синограмма и реконструкция до и после применения коррекции полосовых артефактов [11].

Со временем были предложены методы подавления кольцевых артефактов, использующие усредненную по угловой переменной синограмму. В рамках таких до сих пор остающихся широко распространенными методов используется следующая модель полосовых артефактов синограммы (см. методы нормализации синограммы, например, [3, 12-14]): если \tilde{P} – реально измеренная синограмма (с полосовыми артефактами), P – идеальная искомая синограмма, то для каждого угла просвечивания объекта \theta и ячейки детектора t выполняется соотношение

\tilde{P}(\theta, t) = P(\theta, t)+E(t),

где E(t) – аддитивная ошибка зарегистрированного ячейкой детектора значения (возможно рассмотрение аналогичного уравнения с мультипликативной ошибкой). Последнее равенство можно усреднить по угловой переменной \theta и получить соотношение

\overline{\tilde{P}}(t)=\overline{P}(t)+E(t),

где использованы обозначения средних

\overline{\tilde{P}}(t)=\frac{1}{N_\theta } \sum _\theta \tilde{P} (\theta, t), \: \overline{P}(t)=\frac{1}{N_\theta} \sum _\theta P (\theta, t),

N_{\theta} – количество углов просвечивания объекта. Массив \overline{\tilde{P}}(t) называется усредненной по угловой переменной синограммой (рис. 13). Предполагается, что идеальный усредненный сигнал \overline{P}(t) может быть получен из \overline{\tilde{P}}(t) путем фильтрации некоторым известным фильтром F[\cdot], то есть \overline{P}(t)=F[\overline{\tilde{P}}](t). Отсюда следует формула для определения ошибки E(t)=\overline{\tilde{P}}(t)-F[\overline{\tilde{P}}(t)], обусловливающая наличие полосовых артефактов. Чтобы скорректировать синограмму и устранить полосовые артефакты на ней, остается вычесть вычисленный массив E(t) из каждой строки синограммы, отвечающей определенному углу просвечивания объекта. Для выбора “сглаживающей” фильтрации F[\cdot] усредненной строки синограммы употребляются различные подходы: арифметическое усреднение по некоторому окну, медианный фильтр, гауссовский фильтр, морфологические фильтры, фильтрация в частотной области с помощью уже ранее перечисленных фильтров верхних частот. Недостаток описанных простых в реализации методов – неполное подавление кольцевых артефактов на реконструкции, происходящее из-за того, что эти методы одинаково фильтруют как сильно, так и слабо выраженные полосовые артефакты на синограмме.

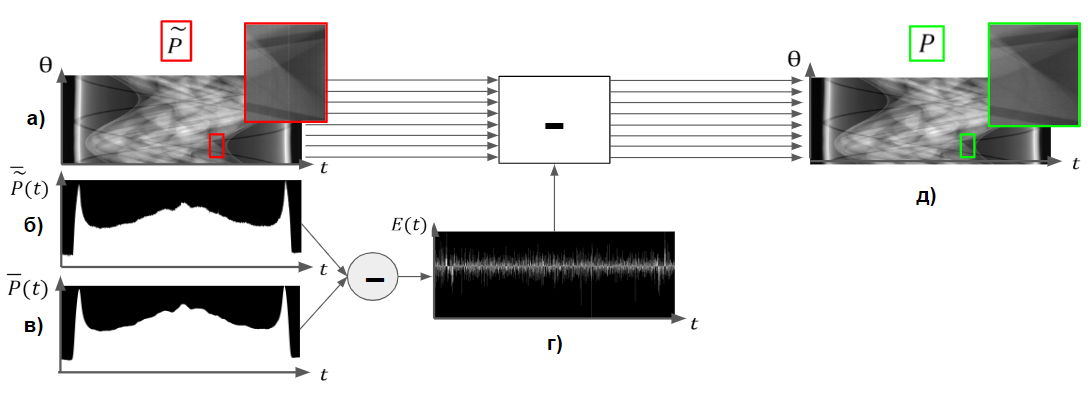
Рис. 13. Метод нормализации синограммы. а) Исходная синограмма с полосовыми артефактами, б) Усредненная строчка синограммы, в) Усредненная отфильтрованная строчка синограммы, г) Разность усредненной строчки синограммы и отфильтрованной усредненной строчки синограммы, д) Синограмма без полосовых артефактов.
Рис. 13. Метод нормализации синограммы. а) Исходная синограмма с полосовыми артефактами, б) Усредненная строчка синограммы, в) Усредненная отфильтрованная строчка синограммы, г) Разность усредненной строчки синограммы и отфильтрованной усредненной строчки синограммы, д) Синограмма без полосовых артефактов.

На пути улучшения описанных методов подавления кольцевых артефактов, использующих усредненную строку синограммы, может производиться фильтрация не всей усредненной строки, а лишь той часть, в которой были задетектированы полосовые артефакты. Так, процедуру коррекции полосовых артефактов на синограмме разбивают на 2 или 3 шага: детекция полосовых артефактов и последующая фильтрация усредненной строки синограммы в областях обнаруженных артефактов [15, 16] или детекция артефактов, их классификация на несколько групп (например, артефакты от битых пикселей, неоткалиброванных пикселей, артефакты от непостоянной интенсивности источника излучения) и последующая фильтрация задетектированных областей с артефактами на усредненной строке синограммы, причем к каждой группе артефактов применяется отдельный фильтр [2] (рис. 14). Классификация задетектированных артефактов на группы по степени их выраженности на синограмме обычно представляет собой пороговую классификацию по значениям усредненной строки синограммы. Нередко пороговая классификация может быть неточной, а это в свою очередь может привести к образованию дополнительных кольцевых артефактов. Поэтому требуется более точная модификация пороговой классификации.

Рис. 14. Результаты коррекции методом детекции, классификации полосовых артефактов и фильтрации усредненной строки синограммы [2]: а) до коррекции, б) после коррекции.
Рис. 14. Результаты коррекции методом детекции, классификации полосовых артефактов и фильтрации усредненной строки синограммы [2]: а) до коррекции, б) после коррекции.

Также к третьей группе методов предобработки проекционных данных должны быть отнесены методы, основанные на выделении полосовых артефактов на  синограмме с последующим их удалением с изображения синограммы. Для этого, к примеру, может быть использовано вейвлет-преобразование [1]: над синограммой производится вейвлет-преобразование, выделяются компоненты преобразования, отвечающие вейвлет-функциям с протяженным “вертикальным” носителем-полосой на изображении (будем называть выделенную часть вейвлет-преобразования вертикальной компонентой). Далее, вертикальная компонента, тесно связанная с наличием полосовых артефактов на синограмме, либо зануляется, либо фильтруется в частотной области, после чего производится обратное вейвлет-преобразование, дающее синограмму с менее выраженными полосовыми артефактами. Методы подавления кольцевых артефактов, использующие вейвлет-преобразование, могут создавать дополнительные кольцевые артефакты на реконструкции или плохо подавлять “сильные” кольца. (рис. 15). Высокой эффективностью, стоит дополнить, отличаются методы коррекции полосовых артефактов на синограмме путем оптимизации различных функционалов синограммы, связанных с ее статистическими характеристиками [17, 18].

Рис. 15. Сравнение различных методов подавления кольцевых артефактов [13].
Рис. 15. Сравнение различных методов подавления кольцевых артефактов [13].

Методы постобработки реконструкции (рис. 7, подгруппа группы 3) подавляют кольцевые артефакты после ее завершения, существуют также методы подавления артефактов во время реконструкции. Были предложены методы подавления колец на реконструкции путем минимизации изотропной или анизотропной нормы полной вариации при использовании итерационных алгоритмов реконструкции [19].  Регуляризация в виде анизотропной полной вариации может сохранять резкость изображений с высокочастотными элементами и уменьшать выраженность кольцевых артефактов (рис. 16).

Рис. 16. Метод подавления кольцевых артефактов во время реконструкции: (a), (d) алгоритм реконструкции SART, (b), (e) алгоритм реконструкции SART + изотропная TV-норма, (c), (f)  алгоритм реконструкции SART + анизотропная TV-норма.
Рис. 16. Метод подавления кольцевых артефактов во время реконструкции: (a), (d) алгоритм реконструкции SART, (b), (e) алгоритм реконструкции SART + изотропная TV-норма, (c), (f)  алгоритм реконструкции SART + анизотропная TV-норма.

Методы постобработки реконструкции часто рассматривают изображение реконструкции в полярной системе координат (центр имеющихся концентрических колец может быть найден с помощью кругового преобразования Хафа [20]): в такой системе координат кольца преобразуются в параллельные прямые. Прямые, полученные из кольцевых артефактов, могут быть удалены с помощью фильтров, применяемых для коррекции синограмм. В частности, может быть использовано вейвлет-преобразование в полярной системе координат [21]: вертикальная или горизонтальная составляющая вейвлет-преобразования либо зануляется, либо фильтруется в частотной области (например, гауссовским фильтром), после чего производится обратное вейвлет-преобразование. Переход к изначальной системе координат дает очищенное от кольцевых артефактов изображение реконструкции (рис. 17). Существенное требование таких методов постобработки – точное предварительное определение положения центра колец на изображении реконструкции.

Рис. 17. Метод постобработки на основе вейвлет-преобразования [21]: a) исходная реконструкция, б) реконструкция после подавления кольцевых артефактов.
Рис. 17. Метод постобработки на основе вейвлет-преобразования [21]: a) исходная реконструкция, б) реконструкция после подавления кольцевых артефактов.

Наконец, сегодня к задаче подавления кольцевых артефактов находят применение методы машинного и глубокого обучения. Активно используется техника transfer learning. Для подавления кольцевых артефактов могут быть обучены сверточные нейронные сети [22], на вход которых подаются как исходная синограмма, так и синограмма, предобработанная некоторым классическим фильтром колец (рис. 18), например, описанным выше фильтром, основанным на вейвлет-преобразовании [1, 21]. Нейросетевые методы в задаче подавления кольцевых артефактов во многом еще развиваются, и, быть может, будущее именно за ними.

Рис. 18. Нейросетевой метод подавления кольцевых артефактов [22].
Рис. 18. Нейросетевой метод подавления кольцевых артефактов [22].

Заключения

На сегодняшний день известно достаточно большое количество методов подавления кольцевых артефактов в компьютерной томографии. Классификация методов уже представляется достаточно оформленной.

Заметим, что немалая доля существующих методов не автоматизирована: методы требуют либо непосредственного вмешательства исследователя в процедуру сбора измерений объекта и ее намеренного изменения, либо ручного подбора параметров метода для наилучшей коррекции реконструкции. Неавтоматические методы могут оказаться затратными по времени. Более того, неавтоматизированными методами может уверенно пользоваться лишь специалист, в то время как для других пользователей оптимальное использование того или иного метода может стать большой сложностью. Часть же автоматических методов не универсальна к степени выраженности колец, и их использование может, наоборот, стать причиной появления на реконструкции новых артефактов.

В связи с этим все еще остается актуальной задача разработки автоматических методов коррекции кольцевых артефактов с помощью проекционных данных. Разработкой таких автоматических методов коррекции занимается и наш отдел компьютерной томографии Smart Engines. Будем стараться порадовать тебя, читатель, нашими успехами в решении этой задачи!

До новых встреч, Хабр!

Список литературы

  1. Münch B. et al. Stripe and ring artifact removal with combined wavelet—Fourier filtering //Optics express. – 2009. – Т. 17. – №. 10. – С. 8567-8591.

  2. Rashid S., Lee S. Y., Hasan M. K. An improved method for the removal of ring artifacts in high resolution CT imaging //EURASIP Journal on Advances in Signal Processing. – 2012. – Т. 2012. – №. 1. – С. 1-18.

  3. Ketcham R. A. New algorithms for ring artifact removal //Developments in X-ray tomography V. – SPIE, 2006. – Т. 6318. – С. 216-222.

  4. Hong K. S., Nalcioglu O., Cho Z. H. Velocity Modulated Scanning Technique For The Elimination Of Ring Artifacts In X-Ray Computed Tomography //Physics and Engineering of Computerized Multidimensional Imaging and Processing. – SPIE, 1986. – Т. 671. – С. 67-71.

  5. Davis G. R., Elliott J. C. X-ray microtomography scanner using time-delay integration for elimination of ring artefacts in the reconstructed image //Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. – 1997. – Т. 394. – №. 1-2. – С. 157-162.

  6. Lifton J., Liu T. Ring artefact reduction via multi-point piecewise linear flat field correction for X-ray computed tomography //Optics Express. – 2019. – Т. 27. – №. 3. – С. 3217-3228.

  7. X-ray Computed Tomography Advanced Lab Course. https://www.ph.tum.de/academics/org/labs/fopra/docs/userguide-79.en.pdf

  8. Chesler D. A., Riederer S. J. Ripple suppression during reconstruction in transverse tomography //Physics in Medicine & Biology. – 1975. – Т. 20. – №. 4. – С. 632.

  9. Kruger R. P., Morris R. A. Simulated neutron tomography for nondestructive assays //Imaging Applications for Automated Industrial Inspection and Assembly. – SPIE, 1979. – Т. 182. – С. 158-163.

  10. Axelsson B., Israelsson A., Larsson S. Non-uniformity induced artifacts in single-photon emission computed tomography //Acta Radiologica: Oncology. – 1983. – Т. 22. – №. 3. – С. 215-224.

  11. Raven C. Numerical removal of ring artifacts in microtomography //Review of scientific instruments. – 1998. – Т. 69. – №. 8. – С. 2978-2980.

  12. Kowalski G. Suppression of ring artefacts in CT fan-beam scanners //ieee Transactions on nuclear science. – 1978. – Т. 25. – №. 5. – С. 1111-1116.

  13. Hasan M. K., Sadi F., Lee S. Y. Removal of ring artifacts in micro-CT imaging using iterative morphological filters //Signal, Image and Video Processing. – 2012. – Т. 6. – С. 41-53.

  14. Eldib M. E. et al. A ring artifact correction method: Validation by micro-CT imaging with flat-panel detectors and a 2D photon-counting detector //Sensors. – 2017. – Т. 17. – №. 2. – С. 269.

  15. Yousuf M. A., Asaduzzaman M. An efficient ring artifact reduction method based on projection data for micro-CT images //Journal of Scientific Research. – 2010. – Т. 2. – №. 1. – С. 37-45.

  16. Anas E. M. A., Lee S. Y., Hasan M. K. Removal of ring artifacts in CT imaging through detection and correction of stripes in the sinogram //Physics in medicine & biology. – 2010. – Т. 55. – №. 22. – С. 6911.

  17. Titarenko V. 1-D filter for ring artifact suppression //IEEE Signal Processing Letters. – 2016. – Т. 23. – №. 6. – С. 800-804.

  18. Miqueles E. X. et al. Generalized Titarenko's algorithm for ring artefacts reduction //Journal of synchrotron radiation. – 2014. – Т. 21. – №. 6. – С. 1333-1346.

  19. Ji D. J. et al. Anisotropic total variation minimization approach in in-line phase-contrast tomography and its application to correction of ring artifacts //Chinese Physics B. – 2017. – Т. 26. – №. 6. – С. 060701.

  20. Jha D. et al. Adaptive center determination for effective suppression of ring artifacts in tomography images //Applied Physics Letters. – 2014. – Т. 105. – №. 14.

  21. Wei Z., Wiebe S., Chapman D. Ring artifacts removal from synchrotron CT image slices //Journal of Instrumentation. – 2013. – Т. 8. – №. 06. – С. C06006.

  22. Chang S. et al. A CNN-based hybrid ring artifact reduction algorithm for CT images //IEEE Transactions on Radiation and Plasma Medical Sciences. – 2020. – Т. 5. – №. 2. – С. 253-260.

Комментарии (0)