Работы древнегреческого математика Евклида являются первым известным примером систематического подхода к геометрии. Созданные около 300 г. до н.э. они заложили основы для понимания геометрических фигур. В этом материале мы рассмотрим постулаты Евклида и их влияние на современное понимание геометрии.

Геометрические постулаты Евклида

Евклид основал свою геометрию на нескольких постулатах (предположениях), которые он считал очевидными и логичными:

1. Прямая линия может быть проведена из любой точки в любую другую точку.

2. Конечная прямая может быть продлена на сколь угодно большое расстояние.

3. Окружность может быть построена с любой точкой в качестве центра и с любой длиной в качестве радиуса.

4. Все прямые углы равны между собой.

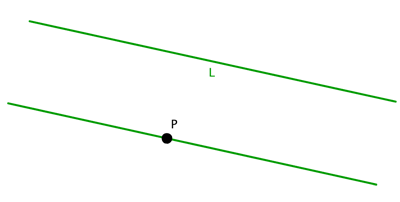
Помимо четырех постулатов, есть и еще один — аксиома параллельности. В нем говорится, что если при проведении прямой, падающей на две прямые, внутренние углы на одной стороне образуют угол меньше двух прямых, то эти две прямые, если их проводить бесконечно, пересекаются на этой стороне.

Математики долго спорили о самоочевидности этого постулата. Все сходятся во мнении, что он не сразу очевиден, ведь нужно визуализировать его с помощью диаграммы. В связи с этим возникает вопрос: если он не самоочевиден, то следует ли принимать его как данность или попытаться доказать его с помощью других постулатов?

Этот вызов был принят греками, потом математиками исламской и иудейской традиций в Средние века, а также европейскими математиками XVII-XVIII веков. Никто из них не добился успеха. Тем не менее, грекам удалось показать, что пятый постулат логически эквивалентен единственности параллельных прямых.

Как идеи Евклида повлияли на разные сферы

Во многих сферах евклидова модель рассуждений сформировала представления о доказательстве, истине и уверенности.

Физика

Евклид не использовал понятие пространства в современном его понимании, но его постулаты подразумевают некоторые свойства пространства, такие как однородность и изотропность.

Более поздние мыслители, особенно начиная с эпохи Возрождения, много говорили о пространстве. И они соглашались с этими ранними предположениями. Идея о том, что пространство должно быть таким, вытекает из принципа достаточного основания: Для всего, что есть, есть причина, по которой оно должно быть таким, как есть, а не иначе.

Принцип достаточного основания так же стар и позволяет объяснять многие вещи в окружающем мире. Например, откуда можно точно знать, что рычаг с равными весами, которые на равных расстояниях от точки опоры, должен находиться в равновесии? Но нет никаких причин для того, чтобы рычаг опускался с любой стороны. Это означает, что он не должен опускаться ни с одной, поэтому он уравновешивается.

Сторонником достаточного основания был математик XVII века Готфрид Вильгельм Лейбниц, который считал, что Бог использовал этот принцип наряду с законами логики при создании Вселенной. А раз Бог создал ее рационально, то люди могут в ней разобраться.

Наглядная иллюстрация «прозрачности» Вселенной — открытие первого закона движения Ньютона. Интересно, что этот закон был выявлен независимо друг от друга Декартом и Пьером Гассенди за пятьдесят лет до Ньютона. Закон утверждает, что объект, находящийся в движении, будет продолжать двигаться по прямой с постоянной скоростью, если на него не будет действовать внешняя сила. Но почему это так?

Объект продолжает двигаться прямолинейно, потому что у него нет веских причин менять направление — все направления одинаково верны. Он сохраняет постоянную скорость, потому что нет причин ускоряться или замедляться — все точки в пространстве одинаковы, поэтому объект не отдает предпочтения одному месту перед другим. По той же логике объект, который находится в состоянии покоя, остается неподвижным, если на него не действует внешняя сила.

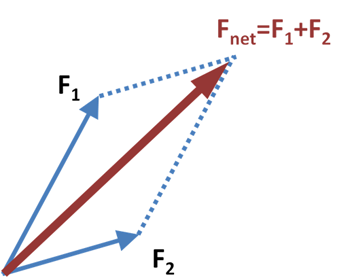
Принцип достаточного основания — это мощная концепция, которая предполагает, что наше жизненное пространство совпадает с пространством, определяемым евклидовой геометрией. Поэтому неудивительно, что мышление XVII и XVIII веков было полностью евклидовым. Например, физика Ньютона неявно зависела от пятого постулата Евклида, который необходим для понимания свойств параллелограмма сил.

Зависимость от пятого постулата объясняет, почему математики XVIII века потратили значительные усилия на его доказательство. Его значение выходило за рамки геометрии, ведь казалось, что от него зависит вся научная сфера.

В качестве примера можно привести математика Жозефа-Луи Лагранжа, который так впечатлился силой принципа достаточного основания, что попытался использовать его для доказательства пятого постулата. Хотя его аргументация была несовершенной, тот факт, что выдающийся математик публично связал евклидово пространство с принципом достаточного основания, подчеркивает его значимость.

Философия

Философия в равной степени была пронизана идеями Евклида. Влиятельный философ Иммануил Кант сказал, что пространство — это то, что существует в человеческом сознании, и у каждого в сознании есть одно и то же уникальное «пространство». Для Канта это пространство должно быть евклидовым.

Кант использовал доказательство Евклида о том, что сумма углов в треугольнике равна двум прямым углам. Это было необходимо ему для демонстрации возможности понимания сложных истин о нефизических сущностях. Доказательство включает в себя геометрические построения, которые, по мнению Канта, не создаются на бумаге, а формируются в ментальном пространстве разума.

Интересно, что доказательство Евклида опирается на пятый постулат. Это означает, что теорема о сумме углов в треугольнике требует евклидова пространства. Хотя Кант не говорит об этом прямо, он утверждает, что существует только один тип пространства. Следовательно, для Канта любая альтернатива евклидовой геометрии представляется немыслимой.

Философ Вольтер был согласен с истинностью евклидова пространства. Он разделял широко распространенную в XVIII веке идею о том, что консенсус — это признак истины, и говорил: «В геометрии нет сект. Нельзя сказать: "Я — евклидовец, я — архимедовец”. Докажите истину, и весь мир будет придерживаться вашего мнения». Он же писал: «Есть только одна мораль, как есть только одна геометрия».

Искусство и архитектура

Искусство и архитектура раннего Нового времени тоже отражают евклидово представление о пространстве. Вот, например, первая важная перспективная картина эпохи Возрождения.

В современном мире все уже привыкли к двухмерным изображениям, которые выглядят трехмерными, потому что есть фотография, телевидение и смартфоны. В эпоху Возрождения таких вещей не было. Поэтому подобная картина была для них невероятно интересной. И эта реалистичная иллюзия глубины в искусстве Ренессанса явно проистекает из евклидовой геометрии.

Чтобы понять разницу между искусством средневековья и ренессанса, полезно посмотреть на средневековое произведение.

На гобелене люди выглядят такими же огромными, как и замок. Несмотря на то, что это прекрасное произведение искусства, в нем нет убедительной трехмерности. Однако в эпоху Возрождения появляется совсем другое пространство.

Геометрия, которую использовали при создании произведений искусства эпохи Возрождения, является буквально евклидовой. Результаты из «Элементов геометрии» и «Оптики» Евклида необходимы для теории перспективы, которую используют художники.

Архитектура также учит видеть мир евклидовым. Например, в комнате обычно есть множество параллельных линий, стен, которые равноудалены и составляют равные прямые углы с полом. Все эти свойства Евклид доказал с помощью своего пятого постулата.

Что изменилось в понимании Евклидовых правил

В начале XIX века произошла геометрическая революция. Люди поняли, что пространство не обязательно должно быть таким, каким его представлял себе Евклид. Например, размышляя о природе пространства, появляются вопросы: является ли оно вещью или субстанцией? Существует ли оно вообще?

Философия пространства

Философ Кант говорил, что пространство находится в уме. Когда мы делаем геометрическую конструкцию, важны не формы, которые мы рисуем на бумаге, а то, как мы видим их в нашем ментальном пространстве. Мы упорядочиваем восприятия в ментальном пространстве, и его свойства одинаковы для всех людей. У Канта это пространство было евклидовым. Трудно представить себе упорядочивание представлений в неевклидовом пространстве, поэтому, возможно, неевклидовы пространства не столь реальны, как евклидовы.

Но физик Герман фон Гельмгольц так не считал. Например, если посмотреть на отражение в выпуклом зеркале, изображение представляет собой трехмерное неевклидово пространство. Можем ли мы научиться упорядочивать свое восприятие в таком пространстве? Если человек может благополучно передвигаться с помощью выпуклого зеркала автомобиля, то ответ «да».

Можно сказать, что зеркало — это всего лишь иллюзия, а реальным может быть только настоящий евклидов мир. Но так ли это на самом деле? Дальние люди в выпуклом зеркале кажутся меньше, чем они есть на самом деле, но если к ним приложить мерку, то мерка тоже будет казаться намного меньше, поэтому измерения в зеркале будут такими же последовательными, как и в обычном мире.

Человек в зеркале (отражение) может в равной степени настаивать на том, что реален только зеркальный мир. С этим трудно спорить, как говорит Гельмгольц, нет такого геометрического эксперимента, который позволил бы решить вопрос о том, какой из этих миров является реальным. Поэтому, в отличие от Канта, Гельмгольц считал, что постулаты геометрии не продиктованы человеческим разумом или логической необходимостью. Для Гельмгольца вопрос о том, является ли пространство евклидовым или нет, был вопросом опыта.

Была и более радикальная точка зрения. Анри Пуанкаре также считал новую геометрию революционной, но он не соглашался ни с Кантом, ни с Гельмгольцем. Если бы, как говорил Гельмгольц, геометрия исходила из опыта, то она не была бы точной наукой. Тем не менее Пуанкаре знал, что в нашем сознании существует более одного вида пространства. Итак, постулаты геометрии — это не синтетические априорные интуиции (как говорил Кант), не экспериментальные факты (как говорил Гельмгольц) и не необходимые самоочевидные истины (как говорили предыдущие мыслители Декарт и Лагранж). Геометрические аксиомы, согласно представлению Пуанкаре, — это условности.

Как же решить, какими конвенциями пользоваться — евклидовыми или одними из новых? Пуанкаре сказал, что наш выбор может быть обусловлен опытом, но пока мы избегаем противоречий, он остается свободным.

«Что мы должны думать о вопросе: истинна ли евклидова геометрия? Этот вопрос не имеет смысла. С таким же успехом можно спросить, является ли метрическая система истинной, а старые гири и меры — ложными. Одна геометрия не может быть более истинна, чем другая; она может быть только более удобной».

Это был революционный сдвиг во взглядах: математика больше не соответствует реальности, вместо этого мы выбираем математическую модель, которая наилучшим образом выполняет то, что мы хотим от нее получить.

В XX веке выяснилось, что неевклидовы геометрии риманова типа на самом деле более удобны. Ведь именно неевклидова геометрия Римана понадобилась Альберту Эйнштейну, чтобы сформулировать свою общую теорию относительности. Означает ли это, что реальное пространство действительно неевклидово? Пуанкаре мог бы сказать, что неевклидова геометрия — это просто то, что работает.

Психология пространства

Еще до появления неевклидовой геометрии философы, такие как Епископ Беркли, отметили, что мы не видим расстояния. Мы видим только визуальные углы и по ним  делаем вывод о геометрии того, что находится снаружи. Посмотрите на угол комнаты, где пересекаются потолок и две стены.

Изобретение неевклидовой геометрии заставило психологов много думать о подобных вещах. Гельмгольц, например, провел эксперимент, в котором попросил людей, находящихся в темной комнате, разложить маленькие точки света на столе в две параллельные линии, постепенно удаляющиеся друг от друга. Линии, которые люди построили из точек света, оказались не параллельными, а кривыми, уходящими в сторону от наблюдателя. Гельмгольц считал, что визуальное пространство неевклидово. В настоящее время преобладает мнение, что пространство зрительного восприятия не представлено никакой последовательной геометрией.

Лингвист-культуролог Стивен Левинсон показал, что люди в разных культурах имеют иные способы упорядочивания своих представлений, чем во внешнем евклидовом пространстве. В некоторых культурах действительно используют идею фиксированной системы координат в пространстве с использованием четырех кардинальных направлений, как когда мы говорим: «Машина стоит к югу от здания».

Однако в других культурах восприятие пространства упорядочивается скорее с точки зрения отношений между телами. Некоторые делают это с точки зрения индивидуума, говоря: «Машина находится справа от здания». Никаких представлений о пространстве при этом не возникает. И есть даже способ, в котором индивид не участвует, например, когда мы говорим: «Машина стоит перед зданием». Здесь внутренние свойства объекта определяют его местоположение.

В современном обществе системы GPS-навигации трансформируют интуитивное понимание пространства в реляционное. Например, рассмотрим ситуацию, когда необходимо проехать из аэропорта в определенный пункт назначения. Инструкции могут быть следующими: из аэропорта повернуть налево, доехать до определенного съезда на скоростную автомагистраль, а затем повернуть направо. Для возвращения в точку А последовательность действий будет обратная. Несмотря на успешное завершение маршрута, человек может не иметь полного представления о пройденном пространстве.

Культура, искусство и архитектура

Интересным мыслителем на тему пространства был испанец Хосе Ортега-и-Гассет. Ортега использовал новую геометрию, чтобы доказать, что предположение, что наш собственный опыт или ценности являются универсальными, ошибочно. Евклидова геометрия, по мнению Ортеги, была провинциальной. Это была необоснованная экстраполяция локальных наблюдений на всю Вселенную.

По словам Ортеги, реальность организуется таким образом, чтобы быть видимой со всех точек зрения: «Теория относительности Эйнштейна, требующая новых геометрий пространства-времени, способствует гармоничному многообразию всех возможных точек зрения». И не только для математики и физики, но и для политики и культуры. Существует китайская точка зрения, говорит Ортега, которая «полностью оправдана, как и западная».

Новая геометрия вдохновила на художественную свободу. Например, портрет Пабло Пикассо, который написал Хуан Грис в 1912 году. Это хороший пример того, что Ортега назвал «реальностью, организующей себя так, чтобы ее можно было увидеть со всех точек зрения».

Теперь обратимся к архитектуре. Заха Хадид — первая женщина, которая выиграла Притцкеровскую архитектурную премию. В бакалавриате она специализировалась на математике. Вот что она говорит о мире XXI века: «Самое главное — это движение, поток вещей, неевклидова геометрия, которая представляет собой новый порядок пространства».

Еще одно всемирно известно здание — это Олимпийский велодром в Лондоне.

Переход от евклидовой к новой геометрии

Евклидова геометрия представляет собой модель, в которой пространство симметрично, стабильно и однородно, и которая предполагает, что все ее законы могут быть поняты разумом. XVIII век стал миром достаточного основания: симметричный, уравновешенный, основанный на самоочевидных и необходимых истинах и вписанный в евклидово пространство.

Но это не тот мир, в котором мы живем сейчас, потому что, начиная с XIX века, ученые, художники и архитекторы стали придерживаться новой геометрии. Именно она диктует свои порядки пространства, помогает применять другие правила, отличные от евклидовых, и создавать прекрасные сооружения и произведения искусства.