Распределённые снапшоты: определение глобального состояния распределённых систем / forpes.ru

08.09.2023 05:37

NorthDragon 0 1100 Источник

Наша команда продолжает развивать Platform V DataGrid — распределённую базу данных в оперативной памяти для высокопроизводительных вычислений. В последнем релизе мы сделали инкрементальные снапшоты, которые быстро снимаются, сохраняют транзакционную целостность и ~~почти~~ не влияют на общую производительность системы.

В рамках работы над этой фичей мы изучили несколько классических статей по распределённым системам, перевода которых на русский ~~кажется~~ не существует. В этом материале представим перевод фундаментальной статьи К. Мани Чанди и Лесли Лэмпорта, посвященной распределённым снапшотам. Всех, кому интересна тема распределённых систем, приглашаю под кат.

K. Mani Chandy

University of Texas at Austin and

Leslie Lamport

Stanford Research Institute

В статье представлен алгоритм, с помощью которого процесс в распределённой системе определяет глобальное состояние, продолжая полезные вычисления. Многие задачи в распределённых системах могут быть выражены в терминах задачи определения глобальных состояний. Например, алгоритм определения глобального состояния помогает решить важный класс задач: вычисление стабильного свойства. Стабильное свойство — то, которое сохраняется: однажды став true, оно остаётся таковым и впоследствии. Примеры стабильных свойств: «вычисление завершено», «система заблокирована» или «все токены в кольце токенов исчезли». Задача определения стабильного свойства заключается в разработке алгоритмов для обнаружения требуемого стабильного свойства. Определение глобального состояния также можно использовать для создания чекпоинтов.

1. Введение

В статье представлены алгоритмы, с помощью которых процесс в распределённой системе может определить глобальное состояние системы, продолжая полезные вычисления. Процессы в распределённой системе взаимодействуют, посылая и получая сообщения. Процесс может записать собственное состояние и сообщения, которые он отправляет и получает, и не более того. Для определения глобального состояния системы процесс должен осуществить взаимодействие с другими процессами, которые должны записать собственные локальные состояния и отправить их .

Процессы не способны записать локальные состояния в точности в один и тот же момент без доступа к общим часам. Мы предполагаем, что у процессов нет общих часов или памяти. Задача состоит в формулировании алгоритмов, с помощью которых процессы запишут собственные состояния и состояния каналов коммуникации так, что сохраненное множество состояний процессов и каналов сформирует глобальное состояние системы. Алгоритм определения глобального состояния пересекается с другими полезными вычислениями: он должен выполняться параллельно с ними, но не изменять их.

Алгоритм определения состояния выполняет роль группы фотографов, снимающих панораму, динамичную сцену — как небо, в котором летают птицы. Но сцена настолько большая, что не может быть снята одним человеком. Фотографы должны сделать несколько снимков и склеить их, чтобы получить полную картину. При этом снимки не могут быть сделаны исключительно одновременно из-за проблем синхронизации. Более того, фотографы не должны мешать процессу, который они фотографируют: например, они не могут сделать так, чтобы во время съемки все птицы в небе оставались неподвижными.

Но всё-таки общий снимок должен быть полезным. Задача, стоящая перед нами — дать определение термину «полезный» и понять, как сделать фотографии.

Теперь опишем важный класс проблем, которые могут быть решены с помощью алгоритма определения глобального состояния. Пусть — предикат, принимающий на вход глобальное состояние распределённой системы , такой, что возвращает true или false для глобального состояния системы . Предикат является стабильным свойством , если из следует $y(S^{'})$ для всех глобальных состояний $S^{'}$ системы , достижимых из глобального состояния системы . Другими словами, если стабильное свойство и истинно в какой-то момент времени работы , тогда истинно в любой момент позднее. Примеры стабильных свойств: «работа системы завершена», «система заблокирована» и «все токены из кольца токенов исчезли».

Несколько задач распределённых систем можно сформулировать как общую задачу вывода алгоритма, с помощью которого процесс в распределённой системе способен определить, обладает ли система стабильный свойством . Обнаружение блокировок [2, 5, 8, 9, 11], обнаружение завершения [1, 4, 10] являются особыми случаями задачи определения стабильного свойства. Детали алгоритма представлены ниже. Основная идея алгоритма в том, чтобы определить глобальное состояние , а потом вычислить , чтобы узнать, присутствует ли стабильное свойство.

Несколько алгоритмов для решения задач обнаружения блокировки или окончания вычислений уже были опубликованы ранее. Gligor и Shattuck [5] заявляют, что многие из опубликованных алгоритмов некорректны и непрактичны. Причина может быть в том, что связи между состояниями локальных процессов, глобальным состоянием системы и точек в распределённых вычислениях тяжелы для понимания. Одна из задач этой статьи — определить эти связи.

Многие распределённые алгоритмы структурированы как последовательность фаз, где каждая фаза состоит из быстрой фазы, выполняющей полезную работу, с последующей частью стабилизации, в которой система крутится бесконечно и бесполезно. Появление стабильного поведения указывает на конец фазы. Фаза похожа на серию итераций в последовательной программе. Они повторяются до тех пор, пока успешные итерации не будут производить изменения, что означает достижение стабильности. Стабильность должна быть замечена, чтобы одна фаза завершилась и следующая началась [10]. Завершение фазы полезной работы не означает завершения работы системы. Когда работа системы завершается, все активности прекращаются: сообщения не отправляются, и состояние процесса не изменяется. Но могут существовать активности в рамках стабильного поведения, которые указывают на окончание фазы вычислений. Сообщения могут быть отправлены и приняты, а процессы могут изменять состояние, но эти активности не служат никакой другой цели, кроме оповещения об окончании фазы. В этой статье мы сосредоточимся на нахождении стабильных свойств системы; прекращение активности — только один пример стабильного свойства.

Строго говоря, такие свойства, как «система заблокирована», не стабильны, если блокировка «снята» и работа перезапущена. Однако для простоты изложения мы должны разделить общую задачу на задачи: (1) определения завершения в одной фазе (и уведомления всех процессов о том, что фаза завершилась), и (2) старта новой фазы. «‑ая фаза работы завершена,» является стабильным свойством. Следовательно, методы, описанные в этой статье, применимы для определения завершения -ой фазы для любого заданного .

В статье мы уделяем внимание только задаче определения стабильных свойств. Задача начала следующей фазы работы не рассматривается, потому что её решение зависит от приложения и будет разным для определения deadlock'а базы данных и определения завершения распределённого вычисления.

Мы должны представить наши алгоритмы в терминах модели системы. Выбранная модель неважна сама по себе: рассуждения можно было изложить в терминах других моделей. Мы должны описать нашу модель неформально и только с необходимым уровнем детализации, чтобы сделать алгоритмы понятными.

2. Модель распределённой системы

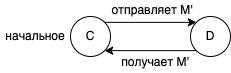
Распределённая система состоит из конечного множества процессов и конечного множества каналов. Она описывается размеченным, направленным графом, в котором вершины являются процессами, а ребра — каналами. Пример показан на схеме 1.

Схема 1. Распределенная система с процессами и каналами .

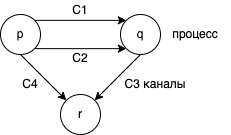
Предполагается, что каналы обладают бесконечными буферами, не содержат ошибок и доставляют сообщения в порядке отправки. Допущение о бесконечном буфере сделано для простоты изложения: ограниченные буферы могут использоваться, если доказано, что ни один процесс не пытается добавить сообщение в заполненный буфер. Задержка доставки каждого сообщения существенная, но конечная. Последовательность сообщений, полученных через канал — подмножество сообщений, отправленных в канал. Состояние канала — это последовательность сообщений, отправленных через него, исключая полученные сообщения.

Процесс определяется множеством состояний, начальным состоянием (из множества) и множеством событий. Событие в процессе — это атомарное действие, которое может изменить состояние самого и состояние максимум одного канала из : состояние может быть изменено с помощью отправки сообщения через (если направлен из ) или получением сообщения через (если направлен в ). Событие определено: (1) процессом , в котором событие возникло, (2) состоянием , в котором находится прямо перед событием, (3) состоянием $s^{'}$ , в котором находится сразу после события, (4) каналом (при наличии), чьё состояние изменено событием, и (5) сообщением (при наличии), переданным через (если направлен от ) или принятое через (если направлен в ). Мы определяем как кортеж из 5 значений $\langle p, s, s^{'}, M, c \rangle$ , где и могут быть заменены на специальное значение , если не изменяет состояния никакого канала.

Глобальное состояние распределённой системы — это множество процессов и состояний каналов. Начальное глобальное состояние — это такое состояние, в котором состояние каждого процесса является начальным и состояние каждого канала — пустая последовательность. Возникновение события может изменить глобальное состояние. Пусть $e = \langle p, s, s^{'}, M, c \rangle$ . Мы говорим, что может произойти в глобальном состоянии тогда и только тогда, если: (1) состояние процесса в глобальном состоянии — это , и (2) если — канал, направленный к , тогда состояние в глобальном состоянии — это последовательность сообщений с на вершине. Мы определяем функцию так, что — это глобальное состояние сразу после появления события в глобальном состоянии . Значение определено, только если событие может возникнуть в глобальном состоянии , в этом случае — это глобальное состояние, идентичное за исключением: (1) состояние в — это $s^{'}$ ; (2) если — это канал, направленный к , тогда состояние в является $c^{'}$ — состояние в и сообщение удалено из вершины; и (3) если — канал, направленный из , то состояние в такое же как состояние $c^{'}$ в с сообщением , добавленным в конец.

Пусть $seq = (e_{i}; 0 \le i \le n)$ — последовательность событий в связанных процессах распределенной системы. Мы определяем, что является работой системы тогда и только тогда, когда событие $e_{i}$ может возникнуть в глобальном состоянии $S_{i}, 0 \le i \le n$ где $S_{0}$ — это начальное глобально состояние и

$S_{i+1} = next(S_{i}, e_{i})\text{ для }0\le i\le n$

Альтернативная модель, основанная на статье Лэмпорта [6], которая представляет работу как частично сортированные множества событий, дана в [7].

Пример 2.1

Для демонстрации определения распределённой системы представим простую систему, состоящую из двух процессов и и двух каналов и $c^{'}$ , как показано на схеме 2.

Схема 2. Простая распределённая система из примера 2.1 и 2.2.

Схема 3. Диаграмма изменения состояния процесса в примере 2.1.

Схема 4. Глобальные состояния и переходы в системе, сохраняющей единственный токен.

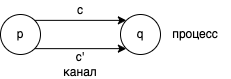
Система содержит один токен, который передаётся от одного процесса к другому, и поэтому мы называем такую систему «сохраняющей единственный токен». Каждый процесс имеет два состояния $s_{0}$ и $s_{1}$ , где $s_{0}$ — состояние, в котором процесс не обладает токеном, а $s_{1}$ — состояние, в котором обладает. Начальным состоянием является $s_{1}$ , а — $s_{0}$ . 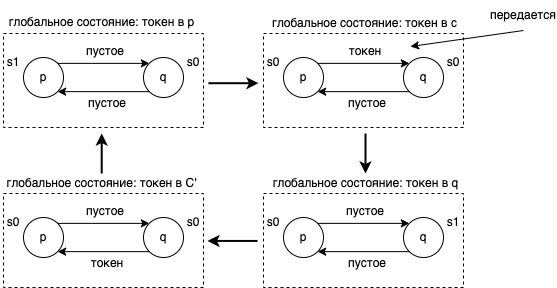Каждый процесс имеет два события: (1) переход из $s_{1}\text{ в }s_{0}$ с отправкой токена, и (2) переход из $s_{0}\text{ в }s_{1}$ при получении токена. Диаграмма изменения состояний для процесса показана на Схеме 3. Изменения глобального состояния показаны на схеме 4.

Работа системы соответствует пути в диаграмме изменения глобального состояния (схема 4), стартуя с начального глобального состояния. Примеры работы системы: (1) пустая последовательность, и (2) $\langle p\text{ отправляет токен}, q \text{ получает токен}, q\text{ отправляет токен} \rangle$ . Следующая последовательность не является работой системы: $\langle p\text{ отправляет токен}, q\text{ отправляет токен} \rangle$ , потому что событие «q отправляет токен» не может возникнуть, пока находится в начальном состоянии $s_{0}$ .

Для краткости, 4 глобальных состояния, в порядке перехода (см. Схему 4), будут называться: (1) в-p, (2) в-c, (3) в-q, и (4) в-c', для обозначения положения токена. Этот пример будет использован позднее для объяснения алгоритма.

Схема 5. Диаграмма изменения состояния процесса в примере 2.2.

Схема 6. Диаграмма изменения состояния процесса в примере 2.2.

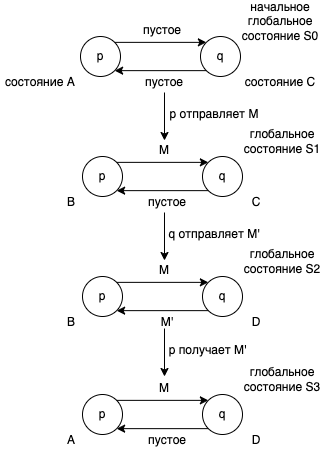
Пример 2.2

Этот пример показывает недетерменированную работу. Недетерменизм играет интересную роль в алгоритме снапшотов.

В примере 2.1 возможно существование в точности одного события в каждом глобальном состоянии. Рассмотрим систему с такой же топологией как в примере 2.1 (см. схема 2), но где процессы и определены диаграммами изменения состояния схема 5 и 6.

Пример полезной работы показан на схеме 7. Читатель должен заметить что может существовать больше одного допустимого перехода из глобального состояния. Например, события " отправляет " и " отправляет $M^{'}$ " могут возникнуть в начальном глобальном состоянии, и следующие состояния после этих событий разные.

3. Алгоритм

3.1. Объяснение шагов алгоритма

Алгоритм записи глобального состояния работает следующим образом. Каждый процесс записывает своё собственное состояние, и два процесса, c которыми связан канал, действуют сообща для записи состояния канала. Мы не можем гарантировать, что состояния всех процессов и каналов будут записаны единовременно, потому что нет глобальных часов; однако мы утверждаем, что записанный процесс и состояние канала формируют «значимое» глобальное состояние системы.

Алгоритм записи глобального состояния пересекается с полезной работой, поэтому он должен выполняться параллельно, но не изменяя её. Алгоритм может отправлять сообщения и требовать от процессов выполнять действия; однако сообщения и вычисления, необходимые для записи глобального состояния, не должны взаимодействовать с полезной работой.

Сейчас мы рассмотрим пример для объяснения шагов алгоритма. В нём мы должны предположить, что можем записать состояние каналов мгновенно; мы откладываем обсуждение, как именно записывается состояние канала. Пусть — канал от к . Цель примера — получить интуитивное понимание связи между моментом времени, в котором состояние канала записано, и моментом времени, в котором должны быть записаны состояния процессов и .

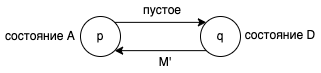
Пример 3.1

Представим систему, сохраняющую единственный токен. Предположим, что состояние процесса p записано в глобальном состоянии в-p, Тогда состояние, записанное для , показывает, что токен находится в . Теперь предположим, что глобальное состояние переходит в в-с(потому что отправляет токен). Предположим, что состояния каналов и $c^{'}$ и процесса были записаны в глобальном состоянии в-c, тогда состояние, записанное для канала , показывает его с токеном, и состояния, записанные для канала $c^{'}$ и процесса , показывают, что он не владеет токеном. Объединённое глобальное состояние, записанное таким образом, покажет два токена в системе, один в и другой в . Но глобальное состояние с двумя токенами недостижимо из начального глобального состояния в системе, сохраняющей единственный токен! Несогласованность возникает из-за того, что состояние записано до того, как отправляет сообщения через , а состояние записано после того, как отправляет сообщение. Пусть — количество сообщений, отправленных через до записи состояния , и пусть $n^{'}$ — количество сообщений, отправленных через до записи состояния . Пример показывает, что записанное глобальное состояние может быть несогласованным, если $n < n^{'}$ .

Теперь рассмотрим альтернативный сценарий. Допустим, состояние записано в глобальном состоянии в-p, затем система переходит в глобальное состояние в-c, и состояния $c^{'}, p\text{ и }q$ записаны в глобальное состояние в-c. Записанное глобальное состояние показывает отсутствие токенов в системе. Пример показывает, что записанное глобальное состояние может быть несогласованным, если состояние записано до того, как отправит сообщение через , а состояние записано после того, как отправил сообщение через , что происходит, если $n > n^{'}$ .

Из этих примеров мы видим, что в общем случае согласованное глобальное состояние требует

$n = n^{'}\text{ (1)}$

Пусть — число сообщений, полученных через до того, как состояние записано. Пусть $m^{'}$ — число сообщений, полученных через до того, как состояние записано. Мы оставляем читателю задачу расширить пример, чтобы показать, что согласованность требует

$m = m^{'}\text{ (2)}$

В каждом состоянии количество сообщений, полученных через канал, не может превышать количество сообщений, отправленных в канал, т. е.

$n^{'} \ge m^{'}\text{ (3)}$

Из уравнений выше имеем

$n \ge m\text{ (4)}$

Записанное состояние канала должно быть последовательностью сообщений, отправленных через канал до того, как записано состояние отправителя, исключая последовательность сообщений, полученных через канал до того, как записано состояние получателя. Т. е. если $n^{'} = m^{'}$ , то записанное состояние должно быть пустой последовательностью, и если $n^{'} > m^{'}$ , то записанное состояние должно состоять из $(m^{'} + 1)го,...,n'го$ сообщений, отправленных через . Этот факт и уравнения (1)-(4) показывают простой алгоритм, с помощью которого q может записать состояние канала . Процесс отправляет специальное сообщениемаркер после -го сообщения, отправленного через (и перед отправкой остальных сообщений через ). Маркер не влияет на полезную работу. Состояние является последовательностью сообщений, полученных после того, как запишет своё собственное состояние, и до того, как получит маркер через . Для того, чтобы уравнение (4) выполнялось, должен записать своё состояние, если это ещё не сделано, после получения маркера через и до того, как получит дальнейшие сообщения через .

Наш пример показывает следующую схему для алгоритма определения глобального состояния.

3.2. Схема алгоритма определения глобального состояния

Правило отправки маркера для процесса . Для каждого существующего канала направленного от :

отправляет один маркер через , и после этого записывает своё состояние до того, как отправит дальнейшие сообщения через :

Правило получения маркера для процесса . При получении маркера через канал :

if q не записало состояние then
    begin
        q записывает собственное состояние;
        q записывает состояние c как пустую последовательность
    end
else
    q записывает состояние c как последовательность сообщений 
    полученных через c после того как состояние q было записано 
    и до того как маркер получен через c.

3.3 Завершение алгоритма

Правила получения и отправки маркера гарантируют, что если маркер получен через каждый канал, тогда каждый процесс запишет своё состояние и состояния всех входящих каналов. Чтобы убедиться в том, что алгоритм записи глобального состояния завершается за конечное время, каждый процесс должен гарантировать, что (L1) ни один маркер не останется навсегда во входящем канале, и (L2) процесс запишет состояние за конечное время после начала алгоритма.

Алгоритм может быть начат одним или несколькими процессами, каждый из которых спонтанно запишет состояние, без получения маркеров от других процессов; мы откладываем обсуждение того, по какой причине процесс изначально записывает своё состояние. Если процесс записывает состояние, и существует канал от к процессу , тогда запишет состояние за конечное время, потому что пошлёт маркер через канал и получит маркер за конечное время (L1). Следовательно, если запишет состояние и есть путь (в графе, представляющем систему) от к процессу , то запишет своё состояние за конечное время, потому что, по индукции, каждый процесс в пути запишет состояние за конечное время. Завершение за конечное время гарантировано, если для каждого процесса : спонтанно записывает собственное состояние или существует путь из процесса , который спонтанно записал состояние к .

В частности, если граф строго связный, и хотя бы один процесс спонтанно записал своё состояние, тогда все процессы запишут состояния за конечное время (указанное в L1 выполняется).

Описанный алгоритм позволяет каждому процессу записать собственное состояние и состояния входящих каналов. Записанные состояния процесса и состояния каналов должны быть собраны и объединены для формирования записанного глобального состояния. Мы не должны описывать алгоритмы сбора записанной информации, потому что такие алгоритмы были описаны в других статьях [4, 10]. Простой алгоритм сбора информации в системе, чья топология обладает сильной связностью: каждый процесс должен отправить записанную информацию через все исходящие каналы, а каждый процесс, получивший информацию в первый раз, копирует ее и распространяет через все исходящие каналы. Таким образом, вся записанная информация будет доставлена до всех процессов за конечное время, что позволит всем процессам определить глобальное записанное состояние.

4. Свойства записанного глобального состояния

Для получения интуитивного понимания свойств глобального состояния, записанного алгоритмом, мы должны изучить пример 2.2. Предположим, что состояние записано в глобальном состоянии $S_{0}$ (схема 7) и состояние, записанное для — это . После записи состояния отправляет маркер через канал . Теперь предположим, что система переходит в глобальное состояние $S_{1}$ , а потом в $S_{2}$ , и потом в $S_{3}$ , пока маркер всё ещё в пути, и маркер получен , когда система в глобальном состоянии $S_{3}$ . При получении маркера записывает своё состояние — это , и записывает состояние — пустая последовательность. После записи состояния отправляет маркер через канал $c^{'}$ . При получении маркера, записывает состояние $c^{'}$ в виде последовательности, состоящей из единственного сообщения $M^{'}$ . Записанное глобальное состояние $S^{*}$ показано на схеме 8. Записывающий алгоритм был запущен в глобальном состоянии $S_{0}$ и завершён в глобальном состоянии $S_{3}$ .

Заметим, что глобальное состояние , записанное алгоритмом, не равняется ни одному глобальному состоянию , которые возникали в процессе работы. Какая польза от алгоритма, если записанное глобальное состояния никогда не возникало? Мы должны ответить на этот вопрос.

Схема 8. Записанное глобальное состояние для Примера 2.2.

Пусть $seq = (e_{i}, 0 \le i)$ будет распределённой работой, и пусть $S_{i}$ будет глобальным состоянием системы сразу же после события $e_{i}, 0 \le i\text{ из }seq$ . Пусть алгоритм будет запущен в глобальном состоянии $S_{l}$ , и пусть он завершится в глобальном состоянии $S_{\phi},0\le l \le \phi$ ; другими словами, алгоритм начат после $e_{l-1}\text{, если }l > 0$ и до $e_{l}$ , и он завершился после $e_{\phi - 1}\text{, если }\phi > 0$ , но до $e_{\phi}$ . Из примера 2.2 мы видим, что записанное глобальное состояние $S^{*}$ может отличаться от всех глобальных состояний $S_{k}, l \le k \le \phi$ .

Мы должны показать, что

$S^{*}$ достижимо из $S_{l}$ , и
$S_{\phi}$ достижимо из $S^{*}$ .

А именно, мы должны показать, что существует вычисление $seq^{'}$ , при котором:

$seq^{'}$ является перестановкой такой, что $S_{l},S^{*}\text{ и }S_{\phi}$ возникают как глобальные состояния в $seq^{'}$ ,
$S_{l} = S^{*}$ или $S_{l}$ возникает раньше, чем $S^{*}$ , и
$S_{\phi} = S^{*}$ или $S^{*}$ возникает раньше, чем $S_{\phi}$ в $seq^{'}$ .

Теорема 1

Существует вычисление $seq^{'} = (e_i^{'}, 0 \le i)$ , при котором:

Для всех i, где $i < l \text{ или } i \ge \phi: e_{i}^{'} = e_{i}$
Подпоследовательность $(e_{i}^{'}, l \le i < \phi)$ является перестановкой подпоследовательности $(e_{i}, l \le i < \phi)$
Для всех i где $i \le l\text{ или }i \ge \phi: S_{i}^{'} = S_{i}$
Существует некоторое $k, l \le k \le \phi\text{ такое, что }S^{*} = S^{'}_{k}$ .

Доказательство.

Событие $e_{i}$ из называется предзаписанным событием тогда и только тогда, когда $e_{i}$ в процессе и записывает состояние после $e_{i}$ из . Событие $e_{i}$ из называется послезаписанным событием тогда и только тогда, когда оно не является предзаписанным событием, т. е. если $e_{i}$ в процессе и записал своё состояние до $e_{i}$ из . Все события $e_{i}, i < l$ являются предзаписанными, и все события $e_{i}, i \ge \phi$ являются послезаписанными событиями в . Может существовать послезаписанное событие $e_{j-1}$ до предзаписанного события для некоторых $j, l < j < \phi$ ; это может возникнуть, только если $e_{j-1}$ и в разных процессах (потому что если $e_{j-1}$ в том же процессе и $e_{j-1}$ послезаписанное событие, тогда и тоже).

Мы должны вывести вычисление $seq^{'}$ с помощью перестановок , где все предзаписанные события возникают до всех послезаписанных событий из $seq^{'}$ . Мы должны показать, что $S^{*}$ — глобальное состояние в $seq^{'}$ после всех предзаписанных событий и до всех послезаписанных событий.

Допустим, что существует послезаписанное событие $e_{j-1}$ перед предзаписанным событием из . Мы должны показать, что последовательность, полученная обменом $e_{j-1}$ и , также является работой. События $e_{j-1}$ и из разных процессов. Пусть будет процессом, в котором произошло $e_{j-1}$ , и пусть будет процессом, в котором произошло . Не может быть сообщения, посланного из $e_{j-1}$ , которое получено в , потому что: (1) если сообщение послано по каналу , когда событие $e_{j-1}$ произошло, тогда маркер должен был быть послан через до $e_{j-1}$ , т. к. $e_{j-1}$ — послезаписанное событие, и (2) если сообщение получено через канал , когда произошло, маркер должен был быть полученным через , до того как произойдет (т. к. канал FIFO), и в этом случае по правилу получение маркера будет послезаписанным событием тоже.

Состояние процесса не изменяется событием $e_{j-1}$ , потому что $e_{j-1}$ происходит в другом процессе . Если — событие, в котором получает сообщение через канал , тогда должно быть сообщением из начала до события $e_{j-1}$ , т. к. сообщение, посланное в $e_{j-1}$ , не может быть получено в . Поэтому событие $e_{j}$ может произойти в глобальном состояние $S_{j-1}$ .

Состояние процесса не изменяется событием $e_{j}$ . Поэтому $e_{j-1}$ может произойти после $e_{j}$ . Поэтому последовательность событий $e_{1},...,e_{j-2},e_{j},e_{j-1}$ является работой. Из рассуждений последнего параграфа следует, что глобальное состояние после обработки событий $e_{1},...,e_{j}$ такое же, как глобальное состояние после вычисления $e_{1},...,e_{j-2},e_j,e_{j-1}$ .

Пусть $seq^{*}$ будет перестановкой , которая идентична за исключением того, что и $e_{j-1}$ поменялись местами. Тогда $seq^{*}$ также будет работой. Пусть $\overline{S_i}$ будет глобальным состоянием непосредственно перед -тым событием в . Из рассуждений предыдущего параграфа,

$\bar{S_{i}}=S_{i}\text{ для всех }i\text{ где }i\ne j\text{.}$

Повторно обменивая послезаписанные события, которые непосредственно следуют за предзаписанными, мы увидим, что существует перестановка $seq^{'}\text{ от }seq$ , в которой:

Все предзаписанные события предшествуют всем послезаписанным событиям,
$seq^{'}$ является работой,
Для всех $i\text{, где }i < l\text{ или }i \ge \phi: e_{i}^{'} = e_{i}$ , и
Для всех $i\text{, где }i \le l \text{ или } i \ge \phi: S_{i}^{'} = S_{i}$ .

Теперь мы должны показать, что глобальное состояние после всех предзаписанных событий и до всех послезаписанных событий в $seq^{'}$ — это $S^{*}$ . Чтобы это сделать, нам надо показать, что:

Состояние каждого процесса в такое же, как и после выполнения работы, состоящей из последовательности предзаписанных событий
Состояние каждого канала в $S^{*}$ это $(\text{последовательность, соответствующая предзаписанным сообщениям, отправленным в } c)$ $- (\text{последовательность, соответствующая предзаписанным сообщениям, полученным в } c)$

Доказательство первой части тривиально. Теперь докажем часть (2). Пусть будет каналом из процесса в процесс . Состояние канала , записанного в $S^{*}$ , является последовательностью сообщений, полученных через после того, как записал своё состояние, и до того, как получил маркер через . Последовательность сообщений, посланных через перед тем, как отправит маркер через , является последовательностью, соответствующей предзаписанным сообщениям, отправленным в . Из этого следует часть (2).

Пример 4.1.

Цель этого примера — показать, как работа $seq^{'}$ выводится из работы . Рассмотрим пример 2.2. Последовательность событий, показанных в работе на схеме 7, является:

$e_{0}$ : отправляет и меняет состояние на (послезаписанное событие)
$e_{1}$ : отправляет $M^{'}$ и меняет состояние на (предзаписанное событие)
$e_{2}$ : получает $M^{'}$ и меняет состояние на (послезаписанное событие)

Т. к. — послезаписанное событие, непосредственно предшествующее — предзаписанному событию, мы меняем их для получения переставленной последовательности $seq^{'}$ :

$e_{0}^{'}$ : отправляет $M^{'}$ и меняет состояние на (предзаписанное событие)
$e_{1}^{'}$ : отправляет и меняет состояние на (послезаписанное событие)
$e_{2}^{'}$ : получает $M^{'}$ и меняет состояние на (послезаписанное событие)

В $seq^{'}$ все предзаписанные события предшествуют всем послезаписанным событиям. Мы оставляем читателю показать, что глобальное состояние после $e_{0}^{'}$ является записанным глобальным состоянием.

5. Определение стабильности

Теперь решим задачу определения стабильности, описанную в разделе 1. Мы изучаем эту задачу, потому что она является парадигмой для многих практических задач, таких как определение распределённого deadlock'а.

Алгоритм определения стабильности определён как:

Вход: стабильное свойство
Выход: логическое (Boolean) значение определено со свойством:
$(y(S_{l})\to definite)\text{ и }(definite\to y(S_{\Phi}))$ ,
где $S_{l}$ и $S_{\phi}$ — глобальные состояния системы, когда алгоритм начат и когда он завершён соответственно (символ $\rightarrow$ означает логическое следствие).

Вход алгоритма — функция (её определение). При выполнении алгоритма значение для какого-то глобального состояния может быть определено процессом в системе, применяя внешне заданную функцию к глобальному состоянию . Под тем, что выходом алгоритма является логическое (Boolean) значение definite, мы имеем в виду, что (1) некоторый специально назначенный процесс (скажем, ) входит и затем остаётся в некотором специальном состоянии, означающем выход definite = true, и (2) входит и остаётся в некотором другом специальном состоянии, означающем выход definite = false.

Из definite = true следует, что стабильное свойство сохранится, когда алгоритм завершится. Однако, из definite = false следует, что стабильное свойство не хранилось, когда алгоритм стартовал. Мы подчёркиваем, что definite = true даёт нам информацию о состоянии системы в момент завершения алгоритма, тогда как definite = false дает нам информацию о состоянии системы на старте алгоритма. В частности, мы не можем сделать вывод из definite = false, что стабильное свойство не сохранится при завершении алгоритма.

Решением задачи определения стабильности является:

begin
    записать глобальное состояние S*;
    definite := y(S*)
end

Корректность алгоритма определения стабильности следует из следующих фактов:

$S^{*}$ достижимо из $S_{l}$ ,
$S_{\phi}$ достижимо из $S^{*}$ (Теорема 1) и
$y(S) \rightarrow y(S^{'})$ для всех $S^{'}$ , достижимых из (определение стабильного свойства).

Благодарности

Отметим вклад J. Misra в формулирование задачи глобального состояния. Мы благодарны E. W. Dijkstra и C. S. Scholten за их комментарии, особенно относящиеся к доказательству Теоремы 1. План текущей версии доказательства был предложен им. Записи [3] Dijkstra по теме предоставляют красочное понимание проблемы определения стабильности. Благодарность C. A. R. Hoare, F. Schneider и G. Andrews, которые помогли нам с подробными комментариями. Мы также благодарны Antia Jones и анонимным рефери за предложения.

Ссылки

CHANDY, K. M., AND MISRA, J. Distributed computation on graphs: Shortest path algorithms. Commun. ACM 25, 11 (Nov. 1982), 833-837.
CHANDY, K. M., MISRA, J., AND HAAS, L. Distributed deadlock detection. ACM Trans. Comput. Syst. I,2 (May 1983), 144-156.
DIJKSTRA, E. W. The distributed snapshot of K. M. Chandy and L. Lamport. Tech. Rep. EWD 864a, Univ. of Texas, Austin, Tex., 1984.
DIJKSTRA, E. W., AND SCHOLTEN, C. S. Termination detection for diffusing computations. Znf. Proc. Lett. 12, 1 (Aug. 1980), 1-4.
GLIGOR, V. D., AND SHATTUCK, S. H. Deadlock detection in distributed systems. IEEE Trans. Softw. Eng. SE-6, 5 (Sep. 1980), 435-440.
LAMPORT, L. Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21, 7 (Jul. 1978), 558-565.
LAMPORT, L., AND CHANDY, K. M. On partially-ordered event models of distributed computations. Submitted for publication.
MAHOUD, S. A., AND RIORDAN, J. S. Software controlled access to distributed databases. INFOR 15, 1 (Feb. 1977), 22-36.
MENASCE, D., AND MUNTZ, R. Locking and deadlock detection in distributed data bases. IEEE Trans. Softw. Eng. SE-& 3 (May 1979), 195-202.
MISRA, J., AND CHANDY, K. M. Termination detection of diffusing computations in communicating sequential processes. ACM Trans. Program. Lang. Syst. 4, 1 (Jan. 1982), 37-43.
OBERMARCK, R. Distributed deadlock detection algorithm. ACM Trans. Database Syst. 7, 2 (Jun. 1982), 187-208

Распределённые снапшоты: определение глобального состояния распределённых систем +8