Несколько дней назад, чтобы доказать что в интернете кто‑то не прав, мне пришлось «считать пиксели», чтобы оценить соотношение размеров двух предметов на фото. Тогда еще я не сообразил сразу, что можно было просто загуглить что‑нибудь вроде «Pixel ruler» и получить размер предметов в пикселях, из которого легко можно получить соотношение. Я же взял подручный MS Paint, вырезал один предмет и уместил его несколько раз внутри другого предмета, сразу узнав во сколько раз один больше другого. Но мне вдруг стало интересно немного автоматизировать этот процесс и решил сделать пиксельную рулетку сам, такую что вводишь заранее уже известный тебе размер некоторого объекта, указываешь его на фото в виде линии, и потом уже другие линии автоматом пересчитываются по отношению к этому размеру. Получилось что‑то в этом роде:

На самом деле задача довольно простая: нужно нагуглить как добавить фото в Canvas и как рисовать линии при помощи мыши. А чтобы вычислить длину нарисованной линии, даже гуглить не пришлось, воспользовался теоремой пифагора:

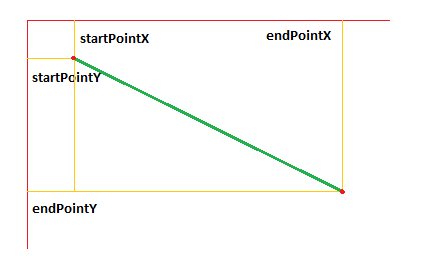
Сложнее было вычислять размеры в перспективе, потому как более близкие предметы с одинаковой шириной, будут смотреться больше чем более дальние. На фото это видно еще лучше:

И я долго‑долго ломал голову как выйти из этой ситуации. Рисовал треугольники, чтобы искать подобие, пытался представить в голове перспективу, но все не было никаких зацепок. Единственное на что обратил внимание, что при изменении угла обзора расстояния до предметов становятся разными:

Эта картинка навела меня на мысль, что отношение размеров на плоскости может быть таким же как и отношение гипотенуз, если из вершины опустить высоту. А вычислить изменение отношений можно через синус. Единственная сложность заключается в том, что один лишь коэффициент, вычисленный через синус угла перспективы (если можно так сказать), не позволит правильно вычислить ширину линейки, поскольку на всем диапазоне измерений в верхней части фото и нижней части он не меняется. Тогда решил менять коэффициент в зависимости от того, на какой высоте от верха фото производится измерение: ну то есть координаты по Y стал пересчитывать не в диапазоне от 0 до высоты картинки, а в диапазоне от sinα и 1+1-sinα (для 60 градусов на котором экспериментировал это 0,866 и 1,134), т.к. нужен коэффициент больше 1 и меньше 1. После такого поправочного коэффициента на перспективу, ширина линейки стала +- одинаковой:

Конечно проблема в том, что помимо размера базового предмета теперь нужно знать еще и угол с которого делали фото, который похоже что проще вычислить методом перебора, но тогда желательно знать 2 размера как минимум, чтобы понимать что угол подобран верно. Кстати на этом фото угол в 55 градусов дает результаты поточнее. Удобно еще и то что поставив угол в 90 градусов, можно снова мерить предметы на плоскости. Код этой "пиксельной линейки" лежит тут , потестить можно вот тут. (Только сейчас обратил внимание что по вертикалии потому и по диагонали перспектива нормально не считается, нужно думать как это исправить)

Прошу сильно не пинать, я знаю что статья как бы и не совсем для хабра, тут такие поделия не сильно приветствуются, но я осмелился опубликовать это для того чтобы послушать критику и предложения. Есть подозрения, что так как я считаю перспективу - это не совсем правильно, но мне даже удивительно что это работает, как минимум на линейке (по горизонтали). Опять же может кого-то это сподвигнет реализовать что-то подобное, и он сможет это сделать в гораздо лучшем виде.