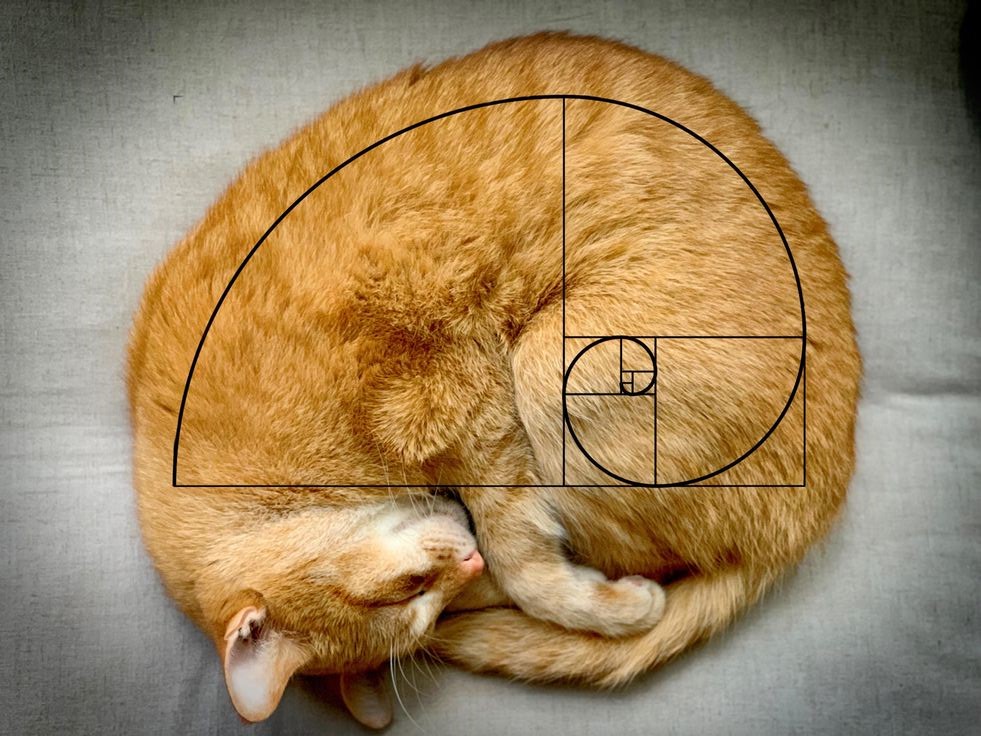
Недавно делал небольшой скрипт для браузера, который может рисовать спираль Фибоначчи поверх фотографий на вебстранице. Все это делалось для того, чтобы проверить свою догадку, по поводу форм встречающихся в природе - вписываются ли они в спираль или нет. Рисовать я ее хотел не поверх котов, а поверх фото, которые немного даже поинтереснее будут, и поэтому и пишу такое длинное предисловие, потому что в отличие от поста в личном блоге, здесь аудитория может отнестись к таком не сильно положительно. Но с другой стороны, все мы люди, поэтому я рискну рассказать об этом эксперименте тут на хабре
В фотографии часто используется правило третей и золотое сечение - фраза буквально из статьи которая выдается первой по поиску в Яндексе, при запросе золотое сечение в фотографии. Вообще есть подозрение, что не все фото делаются специально по этому правилу, но итоге почти все "красивые" фото оказываются соответствующими такому правилу, и человек просто любуется таким фото, не подозревая что любуется математикой. Мало того, любуясь фотографиями девушек, я обратил внимание, что и там часто присутствует такое же золотое сечение - женские формы и изгибы тела очень часто хорошо вписываются в золотую спираль. Смотрите сами:

Для того чтобы проверять в онлайн режиме соответствие форм на форму спирали Фибоначчи, я придумал сделать букмарклет, который бы рисовал прозрачный canvas поверх фотографий, а на нем рисовалась бы сама спираль, размер которой можно было бы изменять так чтобы она вписывалась куда надо. На мое счастье при поиске генератора спирали Фибоначчи на javascript, я сходу нашел решение в виде ответа на stackoverflow.com, где в конце автор ответа дал ссылку на JSFiddle, где можно погонять спираль и понять как она работает. Важно было сделать чтобы спираль рисовалась не только из центра, а ткуда потребуется, и это решилось вставкой простой конструкции:
canvas.addEventListener("mousedown", function (e) {
center.x = e.clientX;
center.y = e.clientY;
}, false);Для того чтобы спираль рисовалась поверх открытой вебстраницы, нужно добавить элемент canvas, который я сделал по размеру всего окна, и который скролится вместе с вебстраницей (свойство css position:sticky) и рисуется поверх других элементов (z-index:2000):
let el = document.getElementsByTagName("body")[0];
let canvas = document.createElement("canvas");
canvas.id = "can";
el.insertBefore(canvas, el.firstChild);
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
canvas.style.zIndex = "2000";
canvas.style.position = "sticky";
canvas.style.top = "0";
ctx = canvas.getContext("2d");А для того, чтобы сделать выход из режима рисования спирали (по кнопке ESC), нужно добавить в код такую конструкцию:
document.addEventListener("keydown", function(){
var x=event.key || event.code;
if(x=="Escape"){
canvas.remove();
}
}) Потом весь код копируется и минимизируется, например при помощи сервиса https://jsminify.org
Полный код
let el = document.getElementsByTagName("body")[0];
let canvas = document.createElement("canvas");
canvas.id = "can";
el.insertBefore(canvas, el.firstChild);
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
canvas.style.zIndex = "2000";
canvas.style.position = "sticky";
canvas.style.top = "0";
ctx = canvas.getContext("2d");
// Assume ctx is canvas 2D Context and ready to render to
var width = ctx.canvas.width;
var height = ctx.canvas.height;
var center = {
x: width / 2,
y: height / 2
};
canvas.addEventListener("mousedown", function (e) {
center.x = e.clientX;
center.y = e.clientY;
}, false);
document.addEventListener("keydown", function(){
var x=event.key || event.code;
if(x=="Escape"){
canvas.remove();
}
})
canvas.addEventListener('mousemove', function(){
var mouse = {};
mouse.x = event.offsetX;
mouse.y = event.offsetY;
if(mouse.x === undefined){ // if firefox
mouse.x = event.clientX;
mouse.y = event.clientY;
}
// Substract offset (so it's centered at 0,0)
mouse.x -= center.x;
mouse.y -= center.y;
drawFibonacciSpiral({x:0, y:0}, mouse);
});
var drawFibonacciSpiral = function(p1, p2){
ctx.clearRect(0, 0, width, height);
// Draw coord axis -> center viewport at 0,0
drawStroke([{x:0, y:-center.y}, {x:0, y:center.y}], center, "gray");
drawStroke([{x:-center.x, y:0}, {x:center.x, y:0}], center,"gray");
// Draw spiral -> center viewport at 0,0
drawStroke(getSpiral(p1, p2, getDistance({x:0,y:0},center)), center);
};
var getDistance = function(p1, p2){
return Math.sqrt(Math.pow(p1.x-p2.x, 2) + Math.pow(p1.y-p2.y, 2));
};
var getAngle = function(p1, p2){
return Math.atan2(p2.y-p1.y, p2.x-p1.x);
};
var drawStroke = function(points, offset, strokeColor){
// Default value
offset = offset || {x:0,y:0}; // Offset to center on screen
strokeColor = strokeColor || "black";
ctx.strokeStyle = strokeColor;
ctx.beginPath();
var p = points[0];
ctx.moveTo(offset.x + p.x, offset.y + p.y);
for(var i = 1; i < points.length; i++){
p = points[i];
ctx.lineTo(offset.x + p.x, offset.y + p.y);
}
ctx.stroke(); // draw it all
};
var FibonacciGenerator = function(){
var thisFibonacci = this;
// Start with 0 1 2... instead of the real sequence 0 1 1 2...
thisFibonacci.array = [0, 1, 2];
thisFibonacci.getDiscrete = function(n){
// If the Fibonacci number is not in the array, calculate it
while (n >= thisFibonacci.array.length){
var length = thisFibonacci.array.length;
var nextFibonacci = thisFibonacci.array[length - 1] + thisFibonacci.array[length - 2];
thisFibonacci.array.push(nextFibonacci);
}
return thisFibonacci.array[n];
};
thisFibonacci.getNumber = function(n){
var floor = Math.floor(n);
var ceil = Math.ceil(n);
if (Math.floor(n) == n){
return thisFibonacci.getDiscrete(n);
}
var a = Math.pow(n - floor, 1.15);
var fibFloor = thisFibonacci.getDiscrete(floor);
var fibCeil = thisFibonacci.getDiscrete(ceil);
return fibFloor + a * (fibCeil - fibFloor);
};
return thisFibonacci;
};
var getSpiral = function(pA, pB, maxRadius){
// 1 step = 1/4 turn or 90º
var precision = 50; // Lines to draw in each 1/4 turn
var stepB = 4; // Steps to get to point B
var angleToPointB = getAngle(pA,pB); // Angle between pA and pB
var distToPointB = getDistance(pA,pB); // Distance between pA and pB
var fibonacci = new FibonacciGenerator();
// Find scale so that the last point of the curve is at distance to pB
var radiusB = fibonacci.getNumber(stepB);
var scale = distToPointB / radiusB;
// Find angle offset so that last point of the curve is at angle to pB
var angleOffset = angleToPointB - stepB * Math.PI / 2;
var path = [];
var i, step , radius, angle, p;
// Start at the center
i = step = radius = angle = 0;
// Continue drawing until reaching maximum radius
while (radius * scale <= maxRadius){
p = {
x: scale * radius * Math.cos(angle + angleOffset) + pA.x,
y: scale * radius * Math.sin(angle + angleOffset) + pA.y
};
path.push(p);
i++; // Next point
step = i / precision; // 1/4 turns at point
radius = fibonacci.getNumber(step); // Radius of Fibonacci spiral
angle = step * Math.PI / 2; // Radians at point
}
return path;
};
Минимизированный код теперь можно поместить в букмарклет, который можно сгенерировать где-нибудь в интернете (вообще была ссылка на блог, но удалил чтобы не посчитали рекламой). А можно воспользоваться уже готовой ссылкой: fiboCheck. Эту ссылку можно добавить на панель ссылок и если увидел фото кота или красивой девушки, то теперь всегда можешь проверить ее фигуру на золотое сечение, просто щелкнув по ссылке.
Букмарклет свою работу в принципе выполняет, но есть несколько нареканий: например, нельзя переворачивать спирать, иногда так было бы удобнее, плюс еще заметил что размер спирали ограничивается, если рисовать ее в левой части канваса. Еще обратил внимание что и сама спираль генерируется немного с переломами.
В общем-то на этом и все о чем хотелось бы рассказать. Сильно не пинайте) В конце вот еще немного красивого:

Комментарии (30)

deamondz
11.05.2024 19:03+12Hidden text

не знал, что "практически идеально" это процентов 10 от видимой линии

GospodinKolhoznik
11.05.2024 19:03+7А вот если девушка прибавит в весе килограмм 40-50, то линия будет ложиться вообще идеально!

Vsevo10d
11.05.2024 19:03+2Если бы эта же шаболда легла с вытянутыми ногами, то видимо стала бы вообще непривлекательной. Что за УГ уровня фишек.нет тут постят?

MountainGoat
11.05.2024 19:03+5Можно в InvokeAI загрузить эту спираль, и сгенерировать кота так, чтобы точно соответствовал кривой.

SquareRootOfZero
11.05.2024 19:03+7Там, где оно более-менее вписывается в часть этой спирали, оно, вроде, и в простую окружность вписывается, как минимум, не хуже? А по-сути, как будто, и окружность не нужна - была бы линия плавная да попа круглая.

AndreySitaev
11.05.2024 19:03+2Надеюсь, пост - ирония. А то полно любителей углядеть магию божественных сечений во всем, что между два и полтора.

alexzzam
11.05.2024 19:03+3Когда говорят про золотое сечение, подразумевают соотношение двух или более размеров. А если рисовать спираль и предполагать, что что-то под неё подходит, оно должно подходить на двух или более витках. А так сама спираль (примерно и на глазок) похожа в любом своём месте на дугу окружности и если считать, что приложить одно место спирали к одному круглому месту на фоточке это "подходит", то да, она подходит ко всему, в чём есть что-то круглое )

Zhuikoff
11.05.2024 19:03+1В спирали два параметра и есть, один стоя другой лёжа. Так что все честно)))

kozlov_de
11.05.2024 19:03+7Просто автор любит котиков и эротические фото.
Спиральки им в укромные места засовывает, шалун

zubrbonasus
11.05.2024 19:03+3У художников то, что вы называете спираль Фибоначчи называют Золотое сечение. Художники утверждают: чтобы картина была привлекательной для зрителя достаточно элементы картины расположить по золотому сечению. Золотое сечение применимо и к фотографии. Если сюжет фотографии расположить так что часть его будет вписываться в Золотое сечение - фотография будет привлекательной для зрителя и поэтому Золотое сечение очень часто используется в художественных произведениях и дизайне.

randomsimplenumber
11.05.2024 19:03+2Если сюжет фотографии расположить так что часть его будет вписываться в Золотое сечение - фотография будет привлекательной для зрителя
Даже если горизонт завален? ;)
Может, наоборот, в привлекательной фотке можно найти золотое сечение. А в очень привлекательной даже спираль Фибоначчи ;))

Squoworode
11.05.2024 19:03+1Даже если горизонт завален? ;)
Да, но только если угол поворота в радианах равен коэффициенту золотого сечения.

AndreySitaev
11.05.2024 19:03Нескромный вопрос: Вам, случайно, не приплачивают за каждое упоминение Золотого сечения?

Weron2 Автор
11.05.2024 19:03Да, я с этой спиралью в первую очередь познакомился как одним из вариантов золотого сечения.

Mionardele
11.05.2024 19:03+1Если наложить спираль золотого сечения на картинку выбирая произвольно масштаб и положение то на любой картине хотя бы одна дуга хорошо впишется. И в искусстве мало кто использовал золотое сечение (например Леонардо да Винчи).
Также в природе десяток подходящих примеров из миллионов это слабый аргумент.
Weron2 Автор
11.05.2024 19:03Я согласен, практически любая плавная линия, на любой фотографии при удачном расположении спирали и ее масштабировании и позиционировании так как надо, впишется в часть этой спирали практически идеально. Собственно этот эксперимент дает такой инструмент для проверки и облегчает проверку этого предположения.
Поэтому и прав самый первый комментатор, который говорит о том что можно натянуть эту спираль почти на любую картинку, так же как и сову на глобус)

randomsimplenumber
11.05.2024 19:03Вот вам идея для программы: ищет на произвольной картинке границу, в которую максимально точно вписывается спираль максимальной длины. Все, можно ранжировать по индексу Фибоначчи;)



datacompboy
Каждый раз когда вижу эти спирали к фотографиям, прям слышу как где-то кричит сова.
Aquahawk
+100. Это как фигуры в техническом анализе. Никто и никогда не показал нормальных критериев, пока всё на глазок типа ок.
w00dLAN
Сова тоже вписывается в спираль Фибоначчи :-)
datacompboy
Нинада!!!!
sophist
*натягивается на
Vsevo10d
Ещё правила третей!!