Привет, Хабр! Как ты уже знаешь, в Smart Engines мы разрабатываем томографическое программное обеспечение. Компьютерная томография (КТ) – это неинвазивный метод исследования внутренних особенностей предмета. На сегодняшний день КТ является одним из основных томографических методов исследования внутренних органов человека, одновременно с этим, КТ – это перспективный инструмент для контроля качества в промышленности.

Исследования КТ проводятся с помощью томографа. Компьютерный томограф – это сложный аппарат, который состоит из 4-х основных частей: 

• Источник рентгеновского излучения

• Детектор

• Подвижный столик или гантри

• Компьютер

Метод компьютерной томографии предполагает 2 основных этапа:

1. Съемка набора трансмиссионных изображений в рентгеновском диапазоне

2. Компьютерная обработка полученных данных

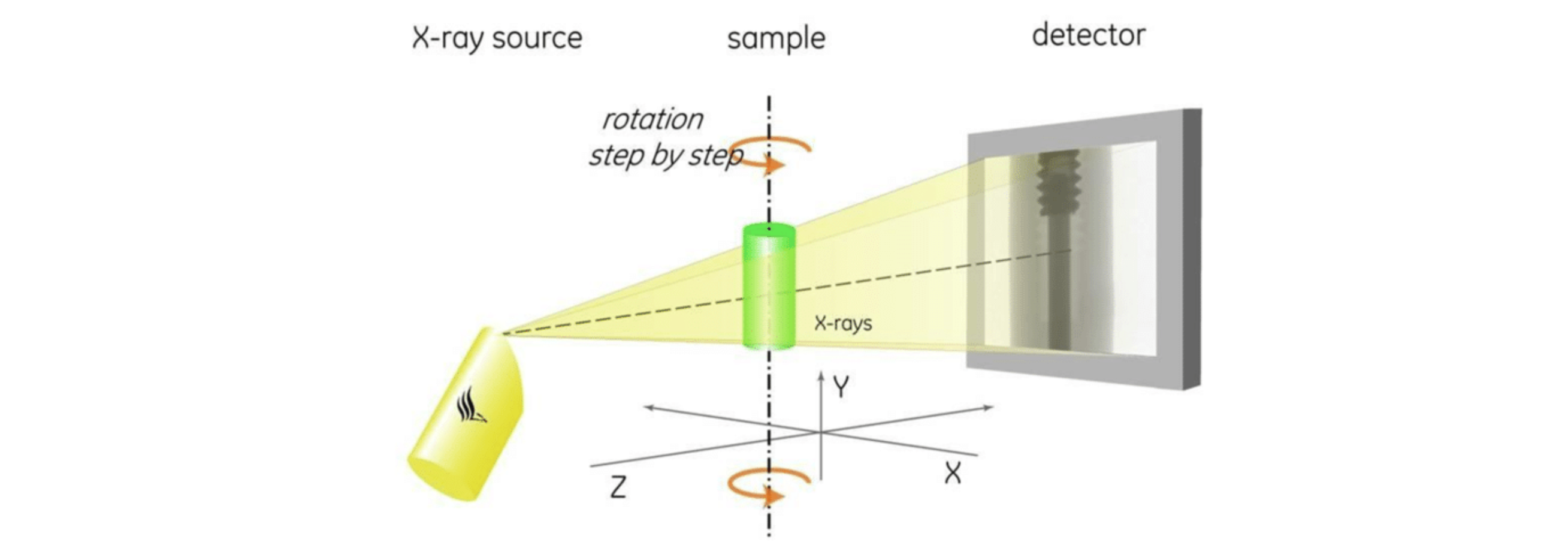
Трансмиссионные изображения, получаемые на первом этапе метода КТ, описывают картину ослабления интенсивности зондирующего излучения при прохождении через объект. Одно трансмиссионное изображение – это результат одного “снятия рентгена”. На первом этапе метода КТ производится сбор целого набора трансмиссионных изображений объекта, которые отличаются ориентацией объекта относительно системы источник-детектор. Второй этап метода КТ предполагает сложную обработку полученного набора изображений, результат которой – воксельная реконструкция исследуемого объекта. 

Процесс разработки томографического обеспечения предполагает работу по многим фронтам: начиная с обработки сырых данных с томографа и создания моделей появления артефактов, заканчивая разработкой алгоритмов КТ-реконструкции и методов анализа. Один из инструментов, помогающий валидировать модели, быстро отсеивать неэффективные идеи и сравнивать различные подходы – это компьютерное моделирование.

Моделирование КТ эксперимента – крайне трудоемкая задача, которая требует внимания ко многим деталям. Во-первых, томографическая установка – это сложный аппарат с широким пространством для выбора параметров и модификаций. Во-вторых, в основе метода КТ лежит сложный по своей сути физический процесс взаимодействия рентгеновских квантов с веществом.

В рамках данной статьи читатель ознакомится с подходом к моделированию поглощения рентгеновского излучения в КТ и узнает роль линейных интегралов в синтезе трансмиссионных изображений.

Линейные интегралы в КТ

В основе метода КТ лежит физический закон Бугера-Ламберта-Бера (ЗБЛБ), определяющий экспоненциальное ослабление интенсивности параллельного монохроматического пучка электромагнитного излучения при распространении его в поглощающей среде. В случае монохроматического излучения поглощательные свойства вещества можно описать линейным коэффициентом поглощения k. Тогда в простейшем виде ЗБЛБ принимает вид:

Где – изначальная интенсивность излучения – координата вдоль направления распространения излучения, а –– интенсивность ослабленного излучения.

Многочисленные эксперименты показали, что в рентгеновском диапазоне излучения ЗБЛБ (1) выполняется с высокой степенью точности.

Если обратить внимание на то, что окружающие нас физические объекты зачастую состоят из разных веществ и материалов, так еще и отличаются по размерам и формам, то захочется немного обобщить формулу (1) до вида (2):

Эта формула так же, как и (1) описывает ослабление интенсивности излучения, но в показателе экспоненты теперь находится интеграл, описывающий поглощающую среду на отрезкевдоль направления распространения излучения. В этой формуле– это локальный линейный коэффициент поглощения, а интеграл

называется линейным интегралом вдоль. Можно сказать, что линейный интегралэто число, показывающее как сильно среда поглощает вдоль направления. Получение набора значений линейных интегралов из трансмиссионных данных – важный промежуточный этап метода КТ, который позволяет сводить решение задачи КТ-реконструкции, например, к задаче решения системы линейных уравнений. 

Давайте рассмотрим в модельном эксперименте процесс получения набора значений линейных интегралов из данных реальных измерений. Для этого, для начала, мы вообразим процесс получения трансмиссионных данных. Для получения трансмиссионного изображения нам понадобится: источник рентгеновского излучения, детектор рентгеновского излучения - из них мы соберем наш виртуальный томограф, и, конечно, нам понадобится объект для исследования. Пусть наш воображаемый источник точечный и он светит в сторону детектора подобно фонарику, а детектор - площадка, снабженная чувствительными к рентгену пикселями. В качестве исследуемого объекта будем использовать апельсин.

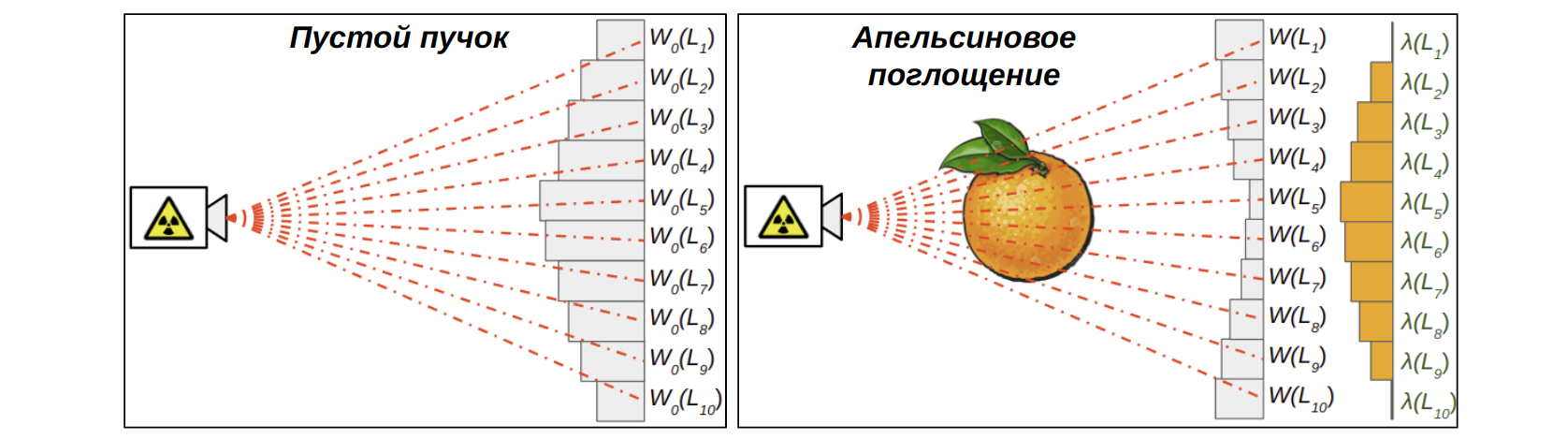
Сейчас все готово для получения трансмиссионного изображения. Мы ожидаем, что детектор зарегистрирует в каждом пикселе p некоторый сигнал, по которому мы сможем оценить интенсивность излучения вдоль направления от источника излучения в центр этого пикселя. Обозначим это направление как. Так как в процессе нашего воображаемого эксперимента выполняется техника безопасности, источник излучения выключен. Для измерения мы включаем источник излучения на время t. Итак, мы получили трансмиссионное изображение, по сути, набор ослабленных интенсивностей вдоль различных направлений. Для того чтобы получить набор не ослабленных интенсивностей , мы в следующем измерении убираем поглощающую среду (в нашем случае мы убираем апельсин) и проводим аналогичные измерения. Полученный в новом измерении отклик детектора называется изображением пустого пучка. Теперь, основываясь на (2), путем логарифмирования мы можем получить набор значений линейных интегралов, используя полученные данные:

Преобразование данных (3) принято называть линеаризацией, а полученные в результате изображения называются линеаризованными.

Наш модельный эксперимент качественно повторяет процесс получения линеаризованных томографических изображений в реальных измерениях, однако в суровой действительности для получения качественной КТ-реконструкции такой простой обработки данных как (3) оказывается недостаточно. В реальном эксперименте мы встречаемся с тем, что среда у нас не чисто поглощающая, источник совсем не точечный и излучает кванты разных энергий, а еще детектор шумит, а часть его пикселей вообще не работают, и так далее по списку. Это все приводит к тому, что на практике используются более сложные преобразования сигналов, чем (3), например, как мы описывали ранее тут.

В примере выше мы рассмотрели процесс получения одного из трансмиссионных изображений. Метод КТ предполагает измерение множества трансмиссионных изображений с разной ориентацией объекта относительно системы источник-детектор, и последующее получение воксельной реконструкции исследуемого объекта.

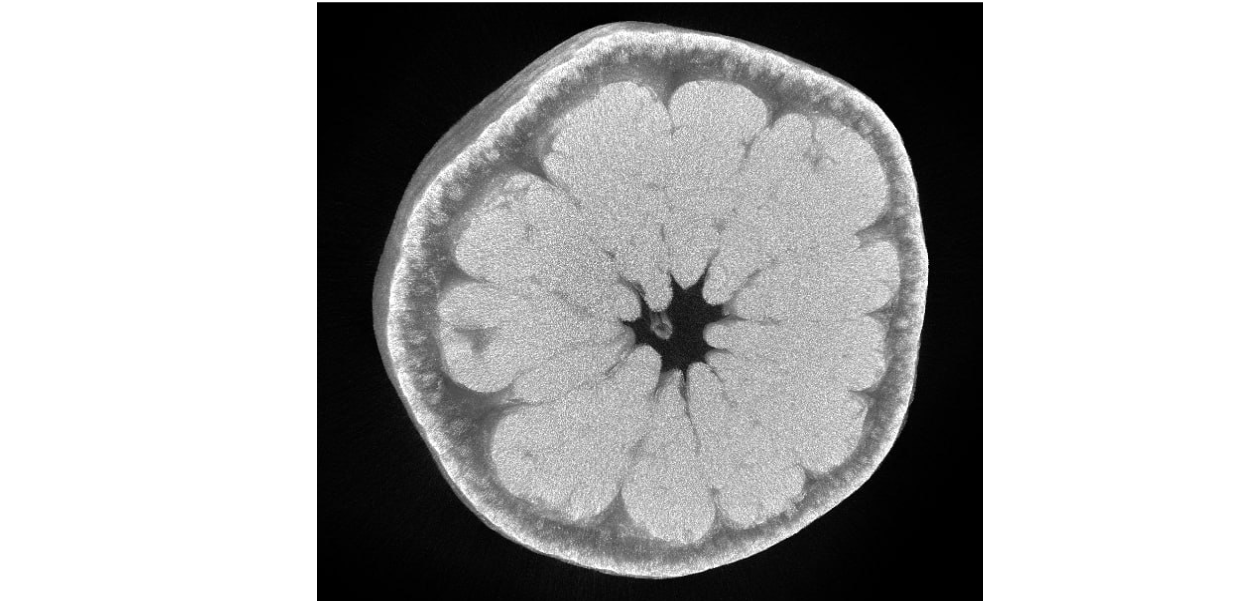
Однако как мы можем проверить, насколько реконструкция точно описывает внутреннее строение исследуемого объекта? В случае с апельсином - мы можем узнать внутреннее строение самым настоящим инвазивным методом – мы можем его просто разрезать, однако с таким подходом далеко не уедешь. Для валидации результата реконструкции необходимо проводить КТ измерения объектов, внутренняя структура которых нам заранее известна. Для этого разработаны медицинские и промышленные тестово-калибровочные фантомы, о которых мы рассказывали в этой статье. К сожалению, подготовить фантомы на все случаи жизни не получится, а получение доступа к множеству разных томографов – нетривиальная задача. Таким образом появляется потребность в численном моделировании, которое позволяет получить трансмиссионные данные на основе цифровых объектов.

Расчет линейных интегралов

Получение синтетических трансмиссионных данных эквивалентно получению набора ослабленных интенсивностей из ЗБЛБ:

Интенсивность изначального излучения можно оценить из реального эксперимента, в крайнем случае - выдумать, однако стоящие в показателе экспоненты значения линейных интегралов просто выдумать не получится. По своему определению линейные интегралы сложным образом связаны между собой – они описывают одну и ту же поглощающую среду вдоль различных направлений. А значит, для начала придется определиться с этой самой поглощающей средой. 

В реальном эксперименте в качестве среды обычно выступает воздух и что-то помещенное в томограф, например, в медицине – это пациент, а в промышленности – сложная деталь. Значит в наших модельных экспериментах нам необходим цифровой объект, будем его называть фантомом – он и выполняет роль поглощающей среды в модельном эксперименте.

Наверное самый известный цифровой фантом в КТ – это фантома Шеппа и Логана (Shepp–Logan phantom [1]). Задумка авторов заключалась в том, чтобы смоделировать одну из плоскостей человеческого черепа с помощью набора эллипсов разных интенсивностей.

Современные цифровые фантомы можно разделить на два основных класса: воксельные и векторные. Оба подхода к представлению фантомов имеют свои плюсы и минусы, однако выбор того или иного представления фантома – это всегда компромисс между реалистичностью и гибкостью.

Векторные фантомы задаются математическими примитивами (это, например, эллипсоиды, параллелепипеды, конусы). Векторное представление фантома позволяет проводить точные расчеты линейных интегралов вдоль различных направлений на основе аналитических формул. Более того, векторное фантомы представимы в любом масштабе без ошибок интерполяции. 

Используя только математические примитивы крайне сложно моделировать изменчивые структуры органов человека и повторять нетривиальные формы деталей механизмов и электрических устройств. В свое время логическим продолжением фантомов на основе математических примитивов стали фантомы на основе параметрических поверхностей (Bezier Surfaces [2], NURBS surfaces [4]). 

Заданные поверхностями фантомы способны принимать формы практически любой сложности. Главный недостаток таких фантомов заключается в сложности их генерации.

Воксельные фантомы - задаются трехмерным массивом чисел, подобно результатам КТ-реконструкции. Огромное преимущество воксельных фантомов над векторными заключается в возможности использования данных реальных экспериментов для создания фантомов.

Хотя такое представление цифровых копий исследуемых объектов кажется наиболее логичным, в процессе модельных экспериментов можно столкнуться с проблемами масштабирования и точных расчетов линейных интегралов. В случае воксельного представления фантома линейный интегралпредставим в виде взвешенной суммы:

Гдепорядковый номер вокселя, который оказался вдоль направления,линейный коэффициент поглощения этого вокселя, а это вес этого вокселя в общей сумме. Именно расчет линейного интеграла в виде взвешенной суммы сильно усложняет моделирование с использованием воксельных фантомов: необходимо определить степень участия каждого из вокселей в ослаблении излучения. Существует множество подходов разной степени точности для решения этой задачи. Эти подходы можно разделить на 3 основные группы по принципу присвоения весов вокселям.

1. “Дискретный луч”. Этот подход предполагает, что в (5) вес вокселя в линейном интегралеможет быть равен только единице или нулю. В рамках данного подхода по направлениюстроится дискретная прямая по воксельному изображению фантома, например, используя алгоритм DDA-линии или алгоритм Брезенхема.

Суммирование производится только по значениям вокселей , которые попали на эту дискретную прямую: 

В этот класс подходов можно также отнести метод быстрого преобразования Хафа (БПХ) [3], который считает суммы вдоль прямых, построенных с использованием сильно ограниченного числа паттернов.

2.“Тонкий луч”. В рамках данного похода направление распространения излучения задается прямой линией, веса вокселям выдаются на основе длины пересечения этой прямой линии с вокселем.

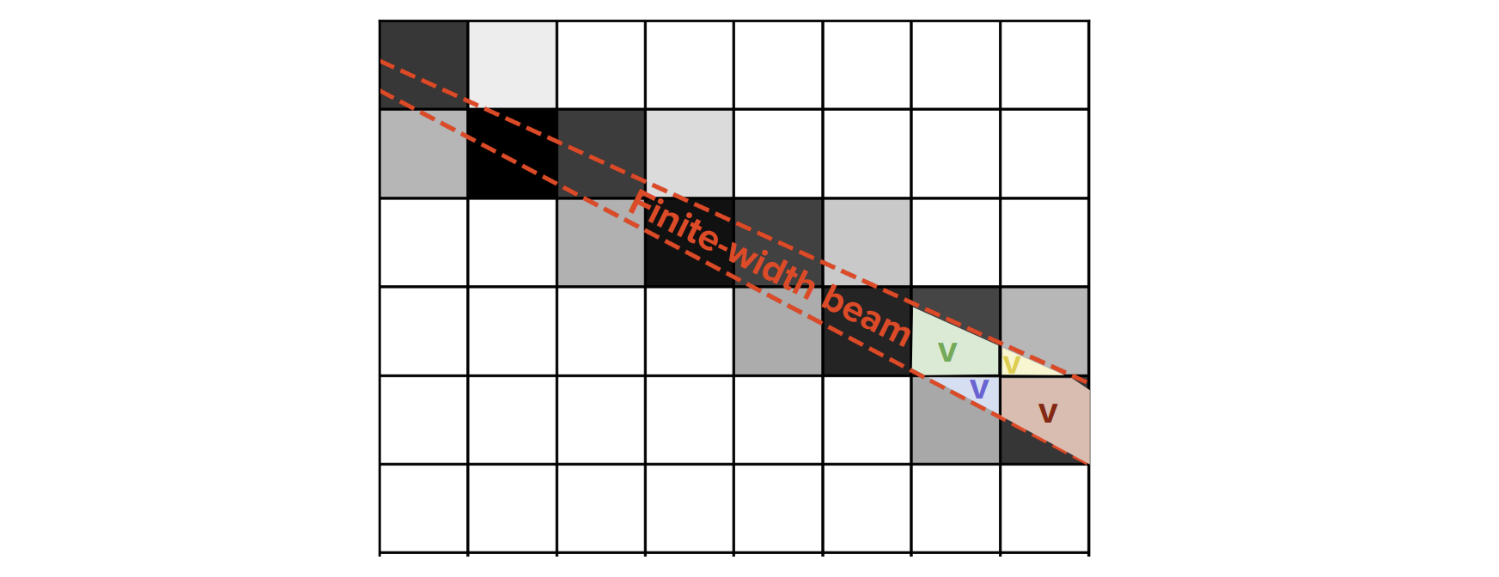
3. “Луч конечной ширины”. Это, скорее всего, самый вычислительно сложный подход, который предполагает использование модели лучей конечной ширины для описания распространения рентгеновских квантов. В рамках этого подхода веса вокселям выдаются на основе объемного или площадного пересечения объемного луча с вокселем.

Вместо заключения

Рост востребованности Компьютерной Томографии (КТ) как важного инструмента для диагностики в медицине и для обеспечения контроля качества в промышленности обуславливает возникновение новых актуальных задач, которые наша команда Smart Tomo Engine успешно решает. О возможностях разработанной нами программы для томографии детальнее можно узнать тут.

В пределах данной статьи, мы ограничились лишь вводным ознакомлением читателей с обширной тематикой моделирования данных КТ. В перспективе мы планируем представить более детальный анализ, охватывающий аспекты моделирования источников излучения и подробное рассмотрение случайных процессов поглощения и рассеяния.

Следите за нашими обновлениями на Хабрe и будьте в курсе последних научных разработок в области КТ. До скорой встречи!