15.10.2023 16:45
Tzimie 83 14000 Источник

Проблема континуума волновала математиков со времен создателя теории множеств, Кантора. Великий математик Гильберт поставил ее на первое место в своем знаменитом списке. В каком-то смысле она считается решенной - только многие не считают это решением, и она по-прежнему занимает умы философов и математиков.

О мощностях множеств

Напомню, что "размер" бесконечных множеств не может быть определен методом пересчета элементов. Вместо этого используется понятие "мощности множества", которое определяется на основе взаимных отображений элементов. Например, любое бесконечное множество целых чисел (например, множество простых чисел) можно пересчитать, присвоив им номера. Все такие множества имеют мощность алеф-нуль (сорри, строчные формулы испортились на хабре и быстро их не починят, как говорит саппорт)

\aleph_0

Множество вещественных чисел, однако, пересчитать нельзя, что доказывается очень элегантно диагональным методом. Мощность множества точек любых конечных и бесконечных фигур на плоскости, в объеме итд также является равномощной множеству вещественных чисел и обозначается как

\aleph_c

Так как множество формул (конечные строки в конечном алфавите) счетно, то большинство вещественных чисел не имеют никакого представления, это безликая масса, безликая настолько, что несмотря на то, что 'безликих' чисел по-прежнему континуум, ни одно из них нельзя привести в пример, показав его явно. Такие безликие элементы называются indiscernibles (замечу, что русской статьи в вики по этому поводу нет, и аналога русского слова мне тоже неизвестно).

Несмотря на то, что из такого множества мы не можем явно предъявить ни одного элемента, для аксиомы выбора нет никаких проблем это сделать. Доказательства, начинающиеся со слов "возьмем произвольный элемент множества" прекрасно работают, если есть аксиома выбора, и поэтому эта аксиома так часто порождает чудовищ - например, парадокс Банаха-Тарского (замечу, что само разрезание сферы в этом парадоксе является indiscernible).

Мы пока познакомились с двумя бесконечными мощностями: счетным и континуумом. Оказывается, есть стандартный способ производить все бОльшие и бОльшие мощности: операция powerset - получение всех подмножеств этого множества. Она обозначается как

powerset(X) = 2^x

- действительно, для конечных множеств число элементов увеличивается именно так. Достоверно известно, что

2^{\aleph_0} = \aleph_c

Гипотеза континуума

Первый вопрос, который возникает, и он действительно возник еще у Кантора, есть ли множество с мощностью между счетной бесконечностью и континуумом? То есть

\aleph_0 < ??? < 2^{\aleph_0} = \aleph_c

Как ни странно, это оказалось очень сложной задачей, не даром она попала в список задач Гильберта под номером 1. Вначале, много лет спустя, Гедель доказал, что существование такого множества не может быть доказано в стандартной теории множеств. Четверть века спустя Cohen доказал, что это утверждение не может быть и опровергнуто. Таким образом, это утверждение является независимым от теории множеств, что сразу порождает две версии теории множеств - где такое множество существует и где его нет.

Если такое множество есть, то оно является indiscernible, потому что если бы это было бы не так, то мы могли бы доказать его существование, просто приведя пример его построения.

Вот вы зря поверили мне сразу, что таких версий две. Их больше. Во-первых, есть 'нейтральная' версия, которая ничего не говорит о существовании множеств промежуточной мощности. Во-вторых, есть версия с гипотезой континуума - она категорична, таких множеств нет. А вот если мы допустим существование множеств промежуточной мощности, то мы можем аксиоматически утверждать, что таких множеств ровно одно, два, три, 188338, любое количество между 17 и 83, любое конечное число, любое конечное простое число итд.

Интересно, что число таких множеств с промежуточной мощностью не может быть бесконечным по довольно сложным причинам. Но любое конечное число - пожалуйста! Допустимо любое конечное подмножество целых, что дает счетное число вариантов теории.

Есть более сильный вариант гипотезы континуума (CH) - обобщенная гипотеза континуума (GCH). Она утверждает, что не только что

2^{\aleph_0} = \aleph_1 = \aleph_c

но что это верно и для любой мощности:

2^{\aleph_\lambda} = \aleph_{\lambda+1}

GCH сильнее CH и из нее еще следует AC (аксиома выбора).

Философский аспект

Так что, задача решена? (так она и помечена в списке Гильберта)? Формалиста от математики (это не обзывалка) это решение полностью удовлетворит. Для формалиста мы вольны задавать любые аксиомы, и получать разный результат с разными аксиомами.

Для платониста же такой ответ неудовлетворителен, поскольку математика это отражение высшей реальности универсума, и на самом деле решение есть - да или нет. Мы должны просто найти подходящие аксиомы, где решение будет.

Конечно, можно спросить - так в чем проблема? Прими гипотезу континуума (CH), что множеств промежуточной мощности нет, вот и решение. Но CH - это костыль, объявление желаемого результата аксиомой. Как если бы в забагованной функции, которая иногда выдает NaN, мы бы сделали проверку на это значение и выдавали бы, например, 0.0, не исправляя самого бага.

Но поиск такой аксиомы вещь очень сложная, потому что аксиома должна быть простой и самоочевидной - куда проще чем сама CH.

Гедель был платонистом, и хотел найти решение, поэтому начал поиск в сторону высших мощностей, которые идут за

\aleph_0, \aleph_1, ..., \aleph_\omega = \aleph_{\aleph_0}, ..., \aleph_{\aleph_{\aleph_...}}, ...

и много дальше, за недостижимые мощности. Направление поиска оказалось очень плодотворным. Можно было бы ожидать, что теорию множеств можно "гнуть" в любую сторону, добавляя разные аксиомы. Но, видимо, за формулами все же есть реальность, и платонисты правы - все новые аксиомы нанизывались друг на друга, образуя почти правильную нить, уходящую в бесконечность к абсолютному универсуму.

На одном из уровней, который отделял маленькие большие мощности (small large cardinals) от больших больших мощностей (large large cardinals) почти нашлось решение проблемы.

Вселенные

Мало кто из ученых может похвастаться существованием вселенной, названной его именем. Я знаю только три таких ученых: Фон Нейман, Гротендик и Гедель. Причем у Геделя вселенных аж две. Первая не имеет отношения к математике - это вращающаяся вселенная Геделя, где все вращается вокруг всего.

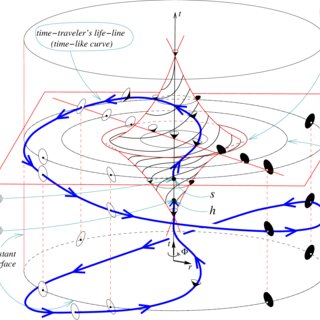
Она является точным решением общей теории относительности для специальных условий. Мало того, что все вращается вокруг всего, так еще и через любую точку пространства времени проходят временной цикл. Создана она была как контрпример принципу Маха. Но мы отвлеклись.

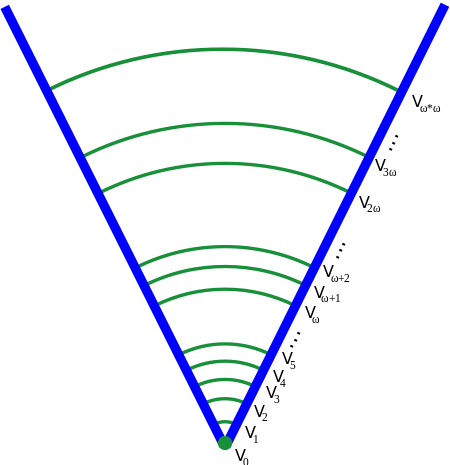
Von Neumann Universe
Von Neumann Universe

Первая математическая вселенная - это V фон Неймана. Она состоит из уровней, при добавлении нового мы берем множество всех подмножеств. V без индекса означает всю вселенную, то есть класс всех множеств (напомню что множество всех множеств - не множество во всех классических теориях множеств. Исключение - New Foundations)

Вселенную Гротендика пропустим. Гедель придумал вселенную L, которая тоже разворачивается этапами - но используя принцип определимости формулами. Каждый следующий уровень собирается из материала предыдущего используя возможные формулы - комбинации множеств, полученных на предыдущих уровнях. Второе название этой вселенной - конструктивная вселенная.

В чем же разница между L и V? V ничего не говорит о свойствах и количестве элементов и возможности их определить. В L же, по построению, не может быть indiscernibles. Таким образом

V = L + indiscernibles

Если принять, что V=L, то сразу решаются многие проблемы, например, CH и GCH - ведь в L нет indiscernibles а значит, обе проблемы решаются автоматически.

Но увы, как оказалось, V=L кастрирует иерархию мощностей, убивая большие большие мощности полностью, а это неинтересно. Хотя граница V=L и пролегает очень, очень высоко, выше всего, куда можно забраться с помощью бесконечного

\aleph_{\aleph_{\aleph_...}}

выше недостижимых мощностей, выше гипер-гипер-недостижимых и еще много выше. Но этого мало.

Даже сам Гедель тоже не верил, что V=L. Увы, надежда оказалась ложной. А жаль, потому что L обладает рядом удобных свойств. Например, все множества в ней определяются одной или несколькими формулами. Мы можем выбрать самую короткую и отсортировать все множества в однозначном порядке. А еще множеств в ней счетное количество, так как множество всех формул счетно.

Что простите?

Парадокс Скулема

Что же такое получается? Мы говорили о несчетных множествах, шли все выше и выше, получали множества чудовищной мощности и теперь оказывается, что всего всех множеств счетное число?

Да, в L это так. Это носит название парадокса Скулема. Теории первого порядка фатально не умеют контролировать мощность своих моделей. Если у теории есть бесконечная модель, то есть модели любой бесконечной мощности.

Модель - это набор "фишек", который удовлетворяет всем формулам теории.

модель теории
модель теории

Но давайте разберемся в парадоксе. Итак, есть множество континуума, которой говорит "Йа несчетно". Мы говорим (в L): а ну-ка, покажи, кто в тебя входит, типа list() в Python. Система задумалась и сгенерила бесконечную строку формул - определений множеств, которые в него входят. Но их счетное количество! Как такое может быть?

Формально парадокс кажущийся, так как утверждение о несчетности множества существует внутри теории, а фишки мы пересчитываем вовне. Это два разных уровня реальности. Но вряд ли вы полностью удовлетворены этим ответом.

Тогда вы можете считать, что определимые элементы в L - это "реперные" точки, которые нарисованы на кривых. Всего точек куда больше, но нам достаточно этих реперных точек.

С вещественными числами все то же самое - мы всегда имеем дело со счетным количеством и обычно этого достаточно, если остальные точки (indiscernibles) ведут себя достаточно мирно. Но это не всегда так, аксиома выбора позволяет построить подмножество вещественных чисел, которое нельзя измерить. Многие чудовища прячутся в тени среди indiscernibles, куда не проникает наш взгляд.

Именно поэтому ни Гедель, ни большинство других математиков не верят в V=L, потому что эта гипотеза делает мир слишком примитивным.

Поздние исследования

Вильям Вудин еще в 90х годах пытался ближе подойти к решению проблемы гипотезы континуума. Сначала он принялся оперировать бесконечной логикой - логикой, где формулы могут быть бесконечной длины, адаптировав ее к теории множеств. Далее он выдвинул правдоподобную гипотезу, которая, если ее принять, решает CH в негативном, но определенном ключе:

2^{\aleph_0} = \aleph_2

то есть между счетной мощностью и мощностью континуума есть ровно одна мощность.

К сожалению, ни бесконечная логика, ни сама гипотеза не удовлетворяют принципу, что аксиома не должна быть, как минимум, сложнее утверждения, которую она доказывает. Вот саму гипотезу континуума понять несложно, а то что написал Вудин я понимаю только по самым верхам. Позже Вудин сам отошел от своей гипотезы и пошел в другом направлении.

Он попытался так расширить L, чтобы V=L не усекала вселенную на таком низком уровне, а содержала почти все большие-большие мощности. Чтобы было лучше понятно, приведу картинку устройства вселенных:

Черный конус - это вселенная V. Для конечных множеств она совпадает с L, но она Уже и ниже V. Она обрывается на уровне аксиомы V=L, убивая интересные большие большие мощности. Вудин пытается создать расширенную вселенную Ultimate-L, которая много выше. Граница V=L отделяет "малые" большие мощности от "больших" больших мощностей.

Выше красной линии находятся "безумно большие большие" мощности. Они столь велики, что там уже перестает работать аксиома выбора AC (а значит и GCH, следовательно, CH там точна ложна!). Но последние исследования Вудина намекают, что там сбоит не только AC, но и ее более простые и куда более очевидные варианты. То есть там живут монстры и, возможно, вся эта конструкция противоречива.

Вудин надеется, что его Ultimate-L решит CH в положительном ключе (то есть от поменял свое мнение)

А зачем вот это все?

Заметьте, что практически вся математика не поднимается выше первых двух бесконечных мощностей - счетного и континуума. С натяжкой, когда мы говорим о подмножествах вещественных чисел мы поднимаемся на уровень второго алефа. Даже первая необычная (сингулярная) мощность

\aleph_\omega = \aleph_{\aleph_0}

нигде не появляется в обычной математике.

Мне известно только три случая, когда существование высших мощностей влияло на что-то вне теории множеств:

  • не так давно выяснилось, что некоторые аспекты машинного обучения зависят от гипотезы континуума

  • некоторые свойства очень быстрорастущих функций доказываются с помощью аксиом существования высоких мощностей - пример

  • неограниченность роста периода laver tables доказывается с помощью аксиомы одной из самых высоких мощностей - однако я думаю что функция растет не настолько быстро, чтобы превысить предел доказуемых утверждений в формальной арифметике - возможно, есть простое доказательство, не использующее теорию множеств.

Так на что это все влияет? Вудин в одной из своих лекций сказал, что есть два варианта: либо когда-нибудь вся эта математика потребуется в Теории Всего, либо нет. Согласитесь, первые вариант был бы интересным - можно себе представить, что, например, в формулу для отношения массы верхнего кварка к нижнему пробрался коэффициент, равный 1, если гипотеза континуума верна и 0 в противном случае.

Но может быть и так, что вся эта кухня никак к физике отношения не имеет. Вудин считает, что это тоже оптимистичный вариант! Потому что это означает, что мы, люди, увидели нечто (очевидно, Вудин платонист), что лежит вне нашей вселенной. От себя добавлю, что это очень перекликается с Гипотезы Математической Вселенной (MUH), созданной Максом Тегмарком.

Комментарии (83)


  1. NeoCode
    15.10.2023 18:48
    #26060458

    А можно ли сказать, что все эти мощности сами по себе образуют некое бесконечное множество? Из того что я понял - счетное множество это нолик, континуум это единичка, 2^0==1. А где нолик и единичка - там и числовая ось, и арифметические операции...

    Ну а есть ли числа между ноликом и единичкой мы знаем - есть, бесконечно много, но не целые. Правда, эта аналогия противоречит тому, что вы написали: "число таких множеств с промежуточной мощностью не может быть бесконечным по довольно сложным причинам" :)


    1. Tzimie Автор
      15.10.2023 18:48
      #26060546

      Я для статьи немного упростил ситуацию. Множество континуума не может быть Aleph_Omega, так как мощность континуума регулярна, а aleph_omega сингулярна. Но, как я понимаю, континуум может быть, например

      \aleph_{\omega+5}

      но я не хотел писать об ординалах (порядковых числах)


      1. NeoCode
        15.10.2023 18:48
        #26061520
        +1

        Еще бы знать что такое "мощность регулярна" и "мощность сигнулярна":)


        1. Tzimie Автор
          15.10.2023 18:48
          #26061564
          +3

          Грубо говоря, регулярная мощность не может быть разложена на меньшее число простых.

          Пример: бесконечная счетная мощность не может быть составлена из конечного числа конечных множеств. Либо надо взять хоть одно бесконечное множество, либо взять бесконечное число конечных множеств.

          Счетное число счетных множеств счетно, поэтому относительно континуума это тоже верно

          Кажется, что так всегда - но нет, не всегда. Сингулярные мощности могут быть разложены на меньшие


        1. Mingun
          15.10.2023 18:48
          #26063086
          +1

          Да тут вообще всю статью надо предварить математическим бэкграундом этак раз в 10, а то и 20 больше самой статьи :) Потому что через слово вводятся какие-то «очевидные понятия» (тм) и галопом по европам скачем дальше.


    1. Abobcum
      15.10.2023 18:48
      #26060664
      +1

      Можно придумать любой математический объект, например множество с дробной мощностью. Только вот зачем это делать?


      1. BugM
        15.10.2023 18:48
        #26060754

        Внезапно может оказаться что это удобно для описания каких-нибудь процессов.

        Чистая математика сама по себе не имеет смысла. Особенно современная теоретическая математика. Но потом внезапно оказывается что физикам без какого-то раздела теоретической и вроде бы бесполезной математики очень неудобно мир описывать.

        Так что пусть развивают. Может и пригодится. И стоит недорого.


        1. Tzimie Автор
          15.10.2023 18:48
          #26060780
          +3

          Это если вы не платонист. Для платониста математика описывает реально существующие вещи


          1. Jeshua
            15.10.2023 18:48
            #26060930
            -1

            Странно быть платонистом более чем через 2000 лет после Платона. Примерно как всерьёз обсуждать устройство мира по Аристотелю. Это ценно с исторической точки зрения, а с практической как-то нелепо. Может, конечно, и существуют сейчас платонисты, Юрий Лоза ведь существует.


            1. Tzimie Автор
              15.10.2023 18:48
              #26060992
              +6

              А ещё странно верить в теорему Пифагора спустя 2500 лет, не правда ли?


              1. Jeshua
                15.10.2023 18:48
                #26061008
                +6

                Вы правы, в теорему Пифагора очень странно верить. Странно верить в то, что доказано. Предупреждая вопрос об аксиомах - в них верить нет необходимости, достаточно отсутствия явных указаний на их противоречивость.

                Что касается платонизма, тут нужно договариваться о значении слов. В общепринятом смысле про платонизм в Википедии можно прочитать вот это:

                Philosophers who affirm the existence of abstract objects are sometimes called Platonists; those who deny their existence are sometimes called nominalists. The terms "Platonism" and "nominalism" also have established senses in the history of philosophy. They denote positions that have little to do with the modern notion of an abstract object. (Выделение моё).


                1. Tzimie Автор
                  15.10.2023 18:48
                  #26061040
                  +1

                  А можно ли верить в теорему, доказанную, например с помощью аксиомы выбора, которую принимают не все?

                  Или верить в неконструктивной доказательство - есть конструктивная математика, где не работает принцип исключённого третьего

                  Если для теории чисел, как правило, такие вопросы не поднимаются, то теория множеств - это на 80 процентов метаматематика, и в ней важна разность философских подходов


                  1. AuroraBorealis
                    15.10.2023 18:48
                    #26061058
                    +2

                    Это всё же не вопрос веры, а скорее вопрос возможности получения полезных выводов. Помимо упомянутого парадокса Банаха-Тарского или разрешения квадратуры круга, аксиома выбора (в виде расширения ZF до ZFC) много где нужна.


                  1. Hardcoin
                    15.10.2023 18:48
                    #26063780

                    Так это же аксиомы. Принимайте, какие удобно.

                    Тем не менее, считать, что в мире абстракций существует абстрактная кровать, а все реальные кровати лишь тени той единственной вряд ли удобно.


                1. Tzimie Автор
                  15.10.2023 18:48
                  #26061042

                  Вы же не будете также укорять геделя, убежденного платониста, в наивности?


                  1. Vytian
                    15.10.2023 18:48
                    #26061640

                    Извините, но основываться на взглядах, мотивациях и убеждениях последовательно разрушавшейся (или возносившейся, как Вам угодно) личности конкретно Курта Гёделя -- довольно опрометчиво. Но, как сказано о другом гении по другому поводу: "ценим ми его не за это".


                    1. Tzimie Автор
                      15.10.2023 18:48
                      #26061658
                      +1

                      Что вы имеете в виду под разрушением личности Геделя?


                      1. ksbes
                        15.10.2023 18:48
                        #26061704
                        -1

                        Ну у него была именно болезненная параноя, как я слышал, которая прогрессировала всю его жизнь. Даже холодильников боялся - потому что могут отравить еду.
                        Непосредственно к математике это имеет отношение слабое, но в от к тому что он платонист - вполне себе прямое. Параноики всегда верят в существование каких-то неведомых объективных сил и сущностей.
                        Подходить чисто формально к вычислениям когда за тобой вселенные люди телепатически следят - довольно сложно.


                      1. Tzimie Автор
                        15.10.2023 18:48
                        #26061722
                        +1

                        Не думаю. Платон вот не страдал паранойей.

                        А то что гении странные - это часто так. Взять хотя бы упомянутого мной в статье Гретендика...


                      1. Tzimie Автор
                        15.10.2023 18:48
                        #26061734
                        +1

                        Вообще найти одного человека с болезнью, который придерживался оспариваемой точки зрения и на этом базировать аргументацию - это где то совсем внизу пирамиды Грэма


                      1. Inkor
                        15.10.2023 18:48
                        #26061752

                        Он наверное имел ввиду что Гедель под конец жизни стал параноиком с психическим расстройством личности. Наверное думает что платонизм его до такого довел, ну или что платонизм следствие этих проблем.


          1. karavan_750
            15.10.2023 18:48
            #26061816

            А платонист вкладывает в множество существующих вещей вещи еще не познанные, неисследованные наукой?
            Если "да", то какими свойствами он наделяет такие объекты?
            Если "нет" и при этом отрицать поиск инструментов для их познания и изучения, то как он познает новое?


            1. Tzimie Автор
              15.10.2023 18:48
              #26062210

              конечно вкладывает

              какими свойствами он наделяет такие объекты? - если они еще не познанные, то их и познают, исследуют


              1. karavan_750
                15.10.2023 18:48
                #26063150

                Но тогда и инструменты познания (в данном контексте -- математика) несуществующего имеют необходимость быть и изучаться.


  1. vics001
    15.10.2023 18:48
    #26060686

    Не совсем понятно, если Универсум фон Неймана  конструируется каждый раз при помощи операции множества подмножеств, то он счетен, так как у него есть механизм построения и L=V.
    Так что скорее всего универсуум определялся как-то более сложно...


    1. Tzimie Автор
      15.10.2023 18:48
      #26060768

      Почему? У V более чем счётное число уровней. Картинка, которую я стащил с интернета да, может вводить в заблуждение...


    1. Tzimie Автор
      15.10.2023 18:48
      #26060772

      Причем число повторений может быть больше, чем максимальная мощность, которая получена к этому шагу (если бы это было бы не так, то мы бы не преодолели первую недостижимую мощность)


  1. kapas19
    15.10.2023 18:48
    #26060994

    Странно, что в вашей статье отсутствует упоминание результатов П.Дж. Коэна (см. например:
    1. Коэн П. Дж., Теория множеств и континуум-гипотеза
    2. Ю.И. Манин, “Проблема континуума”, Итоги науки и техн. Сер. Соврем. пробл. мат., 5, ВИНИТИ, М., 1975, 5–72; J. Soviet Math., 5:4 (1976), 451–501 - https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=intd&paperid=14&option_lang=rus)


    1. Tzimie Автор
      15.10.2023 18:48
      #26061002
      +6

      Как это нет?

      "Четверть века спустя Cohen доказал, что это утверждение не может быть и опровергнуто"


  1. serg_meus
    15.10.2023 18:48
    #26061188
    +4

    Спасибо, благодаря Вашей статье я узнал, что я — платонист


  1. ksbes
    15.10.2023 18:48
    #26061590

    indiscernibles -можно хорошо перевести как "непознаваемые". Или "неписанные" - если хочется больше колорита.


    1. Tzimie Автор
      15.10.2023 18:48
      #26061666

      Скорее "неописуемые", но это слово уже нагружено другим смыслом...


      1. ksbes
        15.10.2023 18:48
        #26061720

        Нет. Здесь речь идёт именно о (невозможности) восприятии объекта , а не о выражении, описании его (там нет корня scribe). Т.е. надо передать смысл что мы не можем эти числа увидеть или понять, а не то что мы их не можем записать.


      1. PleaseKING
        15.10.2023 18:48
        #26062142

        А это разве не трансцендентные числа? Они так и определяются, как все вещественные, которые не алгебраические, то есть не корни алгебраических уравнений.


        1. Tzimie Автор
          15.10.2023 18:48
          #26062220

          нет. трансцендентое число определяется строкой конечной длины, например, 'sqrt(2)', '4*arctan(1)' (вторая строка определяет pi)

          для indiscernibles определяющих их строк нет


          1. PleaseKING
            15.10.2023 18:48
            #26062290

            Гм, Вики с вами не согласна, как и то, как меня учили когда-то: трансцендентные - это все те, что не алгебраические. Впрочем, это вопрос определения, в вашем случае вы расширили список порождающих функций для алгебраических чисел (добавив туда, как явствует из вашего примера, как минимум тригонометрические), и рассматриваете числа вне этого класса. Другими словами, это числа, не описываемые элементарными функциями. Что ж, можно и так, полезно было бы упомянуть, что каждое из них все равно выражается бесконечной непериодической десятичной дробью, так что "пощупать" их, в каком-то смысле, все же можно.


            1. mayorovp
              15.10.2023 18:48
              #26062372
              +4

              Что ж, можно и так, полезно было бы упомянуть, что каждое из них все равно выражается бесконечной непериодической десятичной дробью

              А смысл? Любое действительное число выражается бесконечной десятичной дробью, иррациональное - ещё и непериодической, с чего бы indiscernibles оказались исключением?

              так что "пощупать" их, в каком-то смысле, все же можно

              Разве что при очень богатом воображении (и слабых математических способностях). Если в процессе "щупанья" вы выведите хоть один способ такое число получить - число перестанет быть indiscernible (точнее, окажется что оно никогда и не было indiscernible).


            1. Tzimie Автор
              15.10.2023 18:48
              #26062378

              нет, indiscernibles максимально расширено - допускаются ЛЮБЫЕ формулы и функции, если они корректно и однозначно определены. Кстати вводить тригонометрические функции не нужно, достаточно знака бесконечной суммы для рядов.


            1. Tzimie Автор
              15.10.2023 18:48
              #26062386

              я вообще не говорил про алгебраические числа. я говорил про ВСЕ вещественные


            1. Tzimie Автор
              15.10.2023 18:48
              #26062388
              +2

              это числа, не описываемые элементарными функциями - нет. Это числа, которые ВООБЩЕ НИКАК не описать


            1. domix32
              15.10.2023 18:48
              #26062446
              -1

              Безликие по определению не могут быть представлены отношением в виде формулы или какого-нибудь свойства. Теоретически они не должны быть трансцендентными исходя из этого.


              1. Tzimie Автор
                15.10.2023 18:48
                #26062508
                +2

                Почему? Трансцендентные числа - числа которые не могут быть корнем многочлена бла бла. Среди трансцендентных числе есть безликие и не безликие.

                Пример: число e трансцендентно, но прекрасно описывается формулой - сумма бесконечного ряда.


                1. domix32
                  15.10.2023 18:48
                  #26062676

                  Исходя из определения в вики свойство тоже не должно определять безликих. Если мы невычислимость и трансцендентность не относим к ним, тогда да.


                  1. Tzimie Автор
                    15.10.2023 18:48
                    #26062698
                    +3

                    'безликость' - это мета свойство. Оно не выразимо в самой теории, так как теория оперируют формулами, и следующие вещи являются внешними по отношению к теории:

                    (не)существует доказательство что...

                    теория (не)полна/(не)противоречива

                    модель теории имеет такую то мощность

                    итд

                    на мета уровне 'безликость' неконструктивно определяет множество всех безликих чисел (как разность вещественных и подмножества определяемых) но не определяет ни одно безликое число конкретно


          1. ksbes
            15.10.2023 18:48
            #26062310
            -1

            Вообще по трансцендентным согласен.
            Но вот какая мысль меня посетила:

            Ведь пи, е мы можем записать. Собственно записываем. Можем даже i записать - хотя это вообще невозможное число.
            Т.е. что нам мешает взять и наречь какое-нибудь непознаваемое число как какое-нибудь кси и назвать его так? А мешает то что мы не сможем это кси никак не определить - нет такой математической операции результатом которой являлось бы кси.
            Т.е. эти непознаваемые числа на самом деле - числа бесполезные. Они - типичный "чайник Рассела", лишняя сущность. Что они есть, что их нет - никому ни холодно, ни жарко. Они не могут появиться или участвовать ни каком вычислении и ни в каком доказательстве. У них не может быть каких-либо свойств.
            Что делать? Правильно - звать священника. С бритвой! Можем смело считать что таких чисел просто нет (и не мучиться с переводом).


            1. Tzimie Автор
              15.10.2023 18:48
              #26062402
              +1

              Т.е. что нам мешает взять и наречь какое-нибудь непознаваемое число как какое-нибудь кси и назвать его так?

              Конечно можете. Для аксиомы выбора нет никакой проблемы вытащить число из моря безликих. Только это не будет конкретное число - так что в присвоении ему буквы будет мало смысла

              Но лишней сущностью они не являются - так как они существуют, их не замести под ковер. Более того, подавляющее большинство вещественных чисел - безликие


              1. ksbes
                15.10.2023 18:48
                #26062474

                А как они существуют? Как их существование проявляется?
                Лишняя сущность - она не в плане существования/несуществования а а в плане необходимости для объяснения чего либо. Если числа принципиально бесполезны - их всё равно что нет.

                Хотя если вы платновец - тогда да, существуют. Но в этом и проблема платоновщины :)
                Я тут больше "алгоритмист": для меня математика - это наука описания произвольных алгоритмов (в частности - алгоритмов вычислений, но не только их). Поэтому то для чего принципиально нельзя написать алгоритм - это для меня уже не математика.


                1. Tzimie Автор
                  15.10.2023 18:48
                  #26062498

                  то есть чиcло Хайтина для вас не существует, потому что его нельзя вычислить?

                  вообще теория алгоритмов интересна не только тем, что модно вычислить (всякие классы P, NP, итд), но и тем, что вычислить нельзя

                  https://ru.wikipedia.org/wiki/Константа_Хайтина


                  1. ksbes
                    15.10.2023 18:48
                    #26062604

                    Для "числа Хайтина " алгоритм нахождения есть. Нет алгоритма вычисления всех цифр этого числа (для конкретного языка) - но это другое. Это как с пи - алгоритм есть и он прост - длина окружности на диаметр, но цифр его мы всех никогда не вычислим.

                    И когда я говорю алгоритм - я не только о теории алгоритмов говорю.
                    Например доказательство теоремы Пифагора - это алгоритм того как убедить человека (в том числе и себя) в том, что сумма квадратов катетов равна квадрату гипотенузы (предварительно заставив его признать правоту аксиом геометрии и ещё пару построений).
                    Т.е. это именно рассмотрение всех математический выражений и рассуждений как алгоритмов действий (не обязательно реально исполнимых) необходимых для достижения той или иной цели (вычисления числа или установления истины).

                    В таком рассмотрении все числа - это тоже алгоритмы (измерений чего-либо). Что и поднимает вопрос о существовании "неведомых зверюшек"


                    1. Tzimie Автор
                      15.10.2023 18:48
                      #26062654
                      +3

                      Нет алгоритма вычисления, есть ОПРЕДЕЛЕНИЕ числа. Нельзя определение числа называть алгоритмом

                      Множество всех выражений шире чем множество всех алгоритмов. Есть вполне четко определенные, но алгоритмически неразрешимые проблемы

                      И не надо выдумывать свое определение алгоритма. Возьмем классическое - алгоритм - это программа для машины Тьюринга


                      1. ksbes
                        15.10.2023 18:48
                        #26062786
                        -1

                        Хотелось бы посмотреть как программа для машины Тьюринга приготовит борщ :)
                        Связи с роботизацией понятие алгоритма слега вылезло за пределы счёт, цифр и бумаг.

                        Но вообще даже в математическом смысле через Тьюринга это уже суженное определение. Лучше пользоваться чем-то таким

                        Подводя некоторые итоги: я свою позицию высказал, вашу услышал, принял. Ничего против не имею, но это - не моя позиция :)


                      1. WASD1
                        15.10.2023 18:48
                        #26062964
                        -1

                        Ну так программу написать не проблема.

                        Проблема в том, что не существует машины U+ (способной вычислить не не останавливающуюся программу и возвращающей not-ended) и U++ (способной вычислить бесконечное количество U+)


      1. anoldman25
        15.10.2023 18:48
        #26063238

        я помню их раньше называли "невычислимые"?

        https://ru.wikipedia.org/wiki/Вычислимое_число


        1. mayorovp
          15.10.2023 18:48
          #26064602
          +1

          Это разное. Любое indiscernible невычислимо, но обратное неверно.

          Тут выше уже приводили контрпример - константу Хайтина.


    1. domix32
      15.10.2023 18:48
      #26062390
      +2

      Голосую за "безликих"


      1. Tzimie Автор
        15.10.2023 18:48
        #26062438
        +3


    1. andrshu
      15.10.2023 18:48
      #26062706

      Сфера отсутствия форм или Арупьядхату (санскр. Ārūpyadhātu, или Arūpaloka, тиб. gzugs.med.pa'i khams), Сфера не-форм — в буддийской космологии совокупность миров где отсутствуют формы, я извиняюсь я не иатематик и даже не буддист, но числа непознаваемые навели меня на мысль, что они вот могут присутствовать в таком мире - мир отсутствия форм, в отличие от нашего мира форм где есть числа и все поддается счислению


      1. Tzimie Автор
        15.10.2023 18:48
        #26062712

        Они познаваемы для более высоких сущностей. Я тут об этом писал:

        https://habr.com/ru/articles/536804/

        Аксиома выбора и принципиальные ограничения человеческого разума


        1. andrshu
          15.10.2023 18:48
          #26062816

          а вы точно математик? правильно я понимаю, что математики могут выходить на какое-то ощущение, что кроме нашего мира может существовать другие, ну раз такие необычные числа существуют (которые для нашего мира бесполезны), или точно в формальном плане, это все платонизм, попытка увидеть, то чего нет, игра разума


          1. andrshu
            15.10.2023 18:48
            #26062848

            прочитал вашу статью, ну еще этим вопросом я правильно уловил вектор вашей мысли, но это уже переход к философии, а как же бритва окама, зачем плодить лишние сущности, вселенные и сверхсущесвт, раз существуют какие-то математические парадоксы?


            1. Tzimie Автор
              15.10.2023 18:48
              #26062902

              В математике нет бритвы Окама, а наоборот:

              https://en.wikipedia.org/wiki/Ontological_maximalism


              1. ksbes
                15.10.2023 18:48
                #26062940

                Я бы не сказал, что это "в математике". Это всего лишь одна из многих точек зрения. И не только в математике.


          1. Tzimie Автор
            15.10.2023 18:48
            #26062860

            https://ru.wikipedia.org/wiki/Кантор,_Георг

            Сам Кантор верил в то, что теория трансфинитных чисел была сообщена ему свыше

            Сам Кантор придерживался того же мнения, что и большинство современных нам математиков: любой непротиворечивый математический объект следует считать допустимым и существующим


            1. ksbes
              15.10.2023 18:48
              #26062888

              Поспрашивал математиков вокруг себя - все (оба) единогласно признали сферу в континуально-мерном пространстве (непрерывных на отрезке функций) допустимым но не существующим объектом. Но у нас тут больше материалисты все, а не идеалисты.

              Но вообще да, вопреки обывательскому мнению, философия математики касается. Особенно всяких фундаментальных вещей - как тот же континиум, множество и т.п.

              Сейчас рулит постмодерн - любую формулу или понятие можно интерпретировать как тебе нужно, но ты не имеешь права навязывать свою интерпретацию - только поделится ей и выводами которые из этого следуют.


              1. mayorovp
                15.10.2023 18:48
                #26063034
                +1

                Не существующем? С точки зрения квантовой механики наш мир как раз и описывается континуально-мерным пространством.


    1. andrshu
      15.10.2023 18:48
      #26062802

      Акимчаньяаятана (IAST: Ākiṃcanyāyatana, Ākiñcaññāyatana, тиб. ci.yang.med) — «Сфера, где ничего нет» (буквально отсутствует что бы то ни было) один из миров в буддийской космологии - я конечно извиняюсь -я не математик и не буддист, но размышления о таких цифрах меня на вело на мысль, что такие цифры непознаваемые могут существовать в таком мире, в отличии от нашего, где все почти счисляемо и познаваемо, т..е. числа из мира без форм или неформализуемые


  1. pda0
    15.10.2023 18:48
    #26062442
    +1

    Именно поэтому ни Гедель, ни большинство других математиков не верят в V=L, потому что эта гипотеза делает мир слишком примитивным.

    Это конечно самая мякотка. Повернулись направо (в область знания и доказательств) так сильно, что оказались слева (в области веры). Теоремы зато доказывать просто. "Мамой клянусь" или "Так угодно фон Нейману". :)


    1. ksbes
      15.10.2023 18:48
      #26062558

      Ну когда математика доходит до предела - то да там начинается некоторая вольность в поиске новых сущностей.
      Очень редко кто расписывает свои рассуждение буквально от аксиом. Это слишком много бумаги переводить на банальнейшие утверждения.
      А с помощью выбора из противоречивых аксиом (AC и AD - не единственная пара) можно вообще конструировать математики как из кубиков.


  1. Ivan_Gudoshnikov
    15.10.2023 18:48
    #26062994
    +1

    Даже не доходя до парадокса Банаха-Тарского, насколько я помню, "пример" множества, неизмеримого по Лебегу строится через аксиому выбора. Всегда казалось что что то странное с этой конструкцией, это не "нормальное" описание множества, и почему нельзя дать "нормальное"? Получается, именно что нельзя, странность здесь и заключается в том что неизмеримые множества являются indiscernibles?


    1. Tzimie Автор
      15.10.2023 18:48
      #26063004

      Верно, неизмеримые множества 'безлики' (indiscernibles)

      Из Аксиомы выбора следует закон исключенного третьего, поэтому она так часто создает странные объекты.


  1. yurixi
    15.10.2023 18:48
    #26063362
    -2

    Если посмотреть со стороны, то я бы сделал вывод, что математики рассуждают о существовании "большого пинка" - и не могут свести концы с концами.

    С одной стороны, в самой математике ничего не движется. С другой стороны чтобы что-то существовало надо проявить усилия к появлению, нужен большой пинок. А, возвращаясь обратно к первому варианту, обидно когда тебя пинают. И математиков от этого разрывает изнутри. Как это - пинать самого себя? Раньше математика была защитой от пинков, это что началось-то?

    И это как будто парадокс. Но давно известный. Принцип "Я знаю что ничего не знаю" - это именно к этой истории. Математики лучше всех понимают свою собственную не-математичность. И лучше всего это скрывают, в том числе от себя.

    Статья о том как стыдно быть математиком, только хорошо что не-математикам можно об этом не признаваться. А просто "мы там кое-чего ещё не понимаем". Посмешище! А ничего что это "кое-что" это сама суть?

    Какая-нибудь нулевая аксиома, которая не формализуется, но без понимания которой вся остальная математика - чистейшая безответственная тупость. По типу "Сначала разберись кто и зачем решает, это важно, ведь ограничение в вариантах результата не может быть объективным всегда-всегда".

    Аха-ха. Если пинок завершён, он существует или исчезает? Или существует как потребность в новом пинке? Как оказаться на активной стороне пинка, а не на пассивной? Кому всё это надо? При чём здесь политика? Математики не приспособлены решать философские задачи.


    1. Tzimie Автор
      15.10.2023 18:48
      #26063380
      +2

      Ой. Что вам сделали математики? У Нобеля вроде математик увел невесту, или это легенда, а вы почему не любите математиков?


      1. yurixi
        15.10.2023 18:48
        #26063738
        -1

        Психологическая суть математики - смещать с человека ответственность. И это имеет как позитивные так и негативные стороны, как у религии. А когда математика в процессе познания вынуждает немного взять ответственность на себя, и математик ей говорит "ой, а ты нам не для этого" - здесь уместна особенная ирония.


        1. Hardcoin
          15.10.2023 18:48
          #26064026
          +1

          Любые точные науки смещают ответственность с самого человека. Взял сопромат и построил небоскреб, который стоит сам по себе, а не на вере в строителей. Замечательно же.


          1. yurixi
            15.10.2023 18:48
            #26066120

            Вы упустили что я упомянул позитивные стороны или считаете что они перевешивают негативные? Я вот думаю так просто подразумевать перевешивание это упускать суть негативных сторон.


  1. Ostrie_Brevna
    15.10.2023 18:48
    #26063500
    +3

    Пришёл просто сказать автору спасибо за статью. Одна из самых моих любимых тем в математике :)


  1. Devastor87
    15.10.2023 18:48
    #26064394

    Если такое множество есть, то оно является indiscernible, потому что если бы это было бы не так, то мы могли бы доказать его существование, просто приведя пример его построения.

    Не факт. То, что мы могли бы в этом случае доказать его наличие примером ничего не говорит о вероятности возникновения этого случая ????


    1. Tzimie Автор
      15.10.2023 18:48
      #26064898

      простите, что? вероятности? с какой вероятностью X>10?

      хотя вот пример посложнее: https://ru.wikipedia.org/wiki/Парадокс_Бертрана_(вероятность)


  1. Vitter
    15.10.2023 18:48
    #26066920

    Вики всё же настаивает, что indiscernibles очень даже переводимо на русский, причём термин существует ещё со времён Лейбница.
    indiscernibles = неразличимые


  1. jimmytheneutrino
    15.10.2023 18:48
    #26067222

    Начинаешь читать и к сожаленью косяк сразу во второй формуле. Мощность континуума обозначается просто готической c, а не алефом от нее. Ну и разумеется это разные внщи: алеф от континуума больше алефа от омеги, который не может быть равен континууму даже в ZF.


  1. RolexStrider
    15.10.2023 18:48
    #26067248
    +1

    Удивлен как в этой дискуссии не появилось https://ru.wikipedia.org/wiki/Число_Райо Там есть очень интересный момент (в уточнении): вроде как присутствует некое число из счетного множества (гугол), но по-факту - если разобраться - это число, про которое нельзя сказать "я придумал число еще больше: это число Райо + 1"


    1. ksbes
      15.10.2023 18:48
      #26067278
      +2

      Можно, но чтобы его описать число Райо + 1 потребуется как минимум на один символ больше чем гугол символов на формальном языке теории множеств ("число Райо" - это не формальное описание).
      Так что это вполне нормальное, существующее число.


      1. Tzimie Автор
        15.10.2023 18:48
        #26067466

        А мне вспомнилась шутливая теорема про то "все целые числа интересные". Допустим, это не так. Тогда есть минимальное неинтересное число. Этим оно и интересно!

        Теорема шутливая, но с глубоким философским подтекстом