Уважаемые коллеги! Вашему вниманию предлагается небольшой "этюд выходного дня", посвящённый несколько, скажем так, нетрадиционному способу вычисления медианы массива значений с плавающей точкой. Вкратце — мы сделаем это в несколько проходов по исходному массиву (два для одинарной точности или четыре для двойной), вычисляя медианы по словам, начиная с более значащих, пользуясь при этом только целочисленной арифметикой, что даст возможность в некоторых случаях несколько обогнать по скорости "традиционные" классические алгоритмы. Возможно данная "зарисовка" как идея окажется кому-нибудь полезна.
Прежде чем продолжить — маленький дисклеймер: я никак не связан ни с какой из упоминающихся ниже компаний, пост не носит рекламного характера, код используйте на свой страх и риск.
А началась эта история с рядовой в общем-то задачки — мне нужно было найти медиану рентгеновской картинки (это обычно 12-14 бит изображение) в рамках проверки алгоритма Flat Field Correction. Моя основная рабочая библиотека - NI Vision Development Module, и там есть и среднее и стандартное отклонение, и много чего другого, а вот примитивной медианы не оказалось. На "подхвате" я использую также библиотеки OpenCV либо Intel IPP, но и там навскидку такой функции в готовом виде я не обнаружил (а может плохо искал). Ну не беда — расчехлим компилятор да напишем сами. Да, если вы знаете, как работает гистограммный метод, то можете сразу проматывать примерно до середины, либо прямо до конца, там где результаты замера производительности.
При работе по шестнадцатибитному массиву медиану обычно принято вычислять, пользуясь несложным гистограммным методом. Медиана — это ведь такое значение, которая делит массив (если его отсортировать, разумеется) пополам, так что половина всех остальных элементов по величине будет слева от медианы, а другая половина - справа. Поэтому за один проход по всему массиву строят гистограмму, а дальше перемещаются по ней, останавливаясь в тот момент, когда число отсчётов достигнет половины исходного количества элементов:
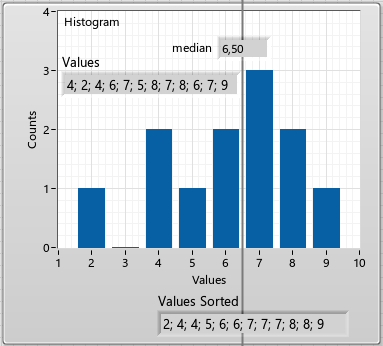
Поскольку я уже относительно немолод и в меру ленив, то для затравки я воспользуюсь ChatGPT. Ну давай, горшочек, вари! Поднатужившись, оно мне выдало вот такой шедевр, приведу его как есть:
unsigned short computeMedian(unsigned short* arr, int size)
{
// Create histogram array
int maxVal = 65536; // Maximum value for unsigned short
int* histogram = (int*)calloc(maxVal, sizeof(int));
// Populate histogram
for (int i = 0; i < size; i++) {
histogram[arr[i]]++;
}
// Find the median value
int medianPos = (size + 1) / 2;
unsigned short median = 0;
int count = 0;
for (int i = 0; i < maxVal; i++) {
count += histogram[i];
if (count >= medianPos) {
median = i;
break;
}
}
// Free memory
free(histogram);
return median;
}
На самом деле неплохо, оно даже знает, что calloc инициализирует память, но есть нюанс — мне даже запускать этот код не нужно, чтобы понять, что это будет работать, только если в массиве нечётное количество элементов. А в чётном случае мы берём среднее арифметическое от значений слева и справа от медианы и мой внутренний перфекционист просит, чтобы значение точно совпадало с референсным. Попросим поправить:
double computeMedian(unsigned short* arr, int size)
{
// Create histogram array
int maxVal = 65536; // Maximum value for unsigned short
int* histogram = (int*)calloc(maxVal, sizeof(int));
// Populate histogram
for (int i = 0; i < size; i++) {
histogram[arr[i]]++;
}
// Find the median position
int medianPos = (size + 1) / 2;
int count = 0;
int medianVal = 0;
// Iterate over histogram to find the median value
for (int i = 0; i < maxVal; i++) {
count += histogram[i];
if (count >= medianPos) {
medianVal = i;
break;
}
}
// If the size is odd, return the median value directly
if (size % 2 != 0) {
return (double)medianVal;
}
// If the size is even, find the next value to compute the median
int nextVal = medianVal + 1;
while (histogram[nextVal] == 0) {
nextVal++;
}
// Compute the median value for even-sized array
return (medianVal + nextVal) / 2.0;
}
Уже лучше, но во-первых, оно почему-то потеряло освобождение выделенной под гистограмму памяти, а во-вторых, этот код будет профукивать истинное значение медианы, если в исходном массиве будут повторяющиеся элементы. Дальнейшие просьбы исправлений будут раздувать код ещё сильнее (а сколько программистов скопипастят его прямо в таком виде?). Пожалуй без работы ChatGPT нас пока что не оставит. Засучиваем рукава и правим код ручками, ну как-то вот так что ли:
double computeMedian(unsigned short* arr, size_t size)
{
size_t* histogram;
double Median;
if (!arr || !size) return -1;
if (!( histogram = (size_t*)calloc(USHRT_MAX + 1, sizeof(size_t)))) return -2;
for (int i = 0; i < size; i++) histogram[arr[i]]++; // Populate histogram
size_t medianPos = (size + 1) / 2, count = 0, medianVal; // Find the median pos
for (medianVal = 0; medianVal <= USHRT_MAX; medianVal++) { // Iterate over histo
count += histogram[medianVal];
if (count >= medianPos) break;
}
if (!(size % 2 || count > medianPos)) { // If the size is even, find the next
size_t nextVal = medianVal;
while (!histogram[++nextVal]);
Median = (medianVal + nextVal) / 2.0; // Middle
}
else Median = (double)medianVal;
free(histogram);
return Median;
}
На код ревью, вероятно, могут возникнуть кое-какие вопросы, но всегда можно свалить на искусственный интеллект, опять же статический анализатор молчит как партизан.
32 бита
Рядовая в общем-то задачка не стоила бы поста на Хабре, да и его бы и не появилось, если бы во время ежевечерней прогулки с собакеным мой внутренний голос ехидно и вкрадчиво не поинтересовался: "— а вот если, предположим, у тебя массив не 16-и, а 32-х битный, то как тогда?". Ведь на гистограмму в четыре с лишним миллиардов элементов никакой памяти не хватит! Поразмышляв немного, я ещё до конца прогулки измыслил простой незатейливый метод — вначале надо пройти по старшим словам, построив гистограмму в 65 килоэлементов как и выше, а затем, отталкиваясь от найденного значения пройти по массиву ещё раз, строя гистограмму уже по младшему слову и уточняя значение медианы. В принципе метод не нов — мы фактически разбиваем весь диапазон на 65536 отрезков, и найдя подходящий отрезок, ищем там окончательное значение. Маленький нюанс есть с частным случаем когда в исходном массиве чётное количество элементов и наша медиана лежит между разными значениями старшего слова. Но если представить в уме отсортированный массив, то станет ясно, что отдельные гистограммы тут уже не нужны, просто слева (для меньшего старшего байта) следует взять максимальное значение младшего байта, а справа (для большего) — минимальное, и потом уже найти среднее, вот и всё:

Я набросал было код на LabVIEW, но пожалуй не стану вас мучить, хоть мы и в хабе "Ненормальное программирование".
На Си оно будет так же, как и в случае 16 бит, вот только гистограмму мы строим по старшим битам, задвигая их направо:
LIBMED_API int MedianU32(unsigned int* ptr, size_t Length, double* med)
{
//...
histo = (size_t*)calloc(USHRT_MAX + 1, sizeof(size_t));
for (int i = 0; i < Length; i++) histo[(ptr[i] & 0xFFFF0000) >> 16]++;
//...
До этого момента всё ровно как и раньше:
uint64_t medianPos = (Length + 1) / 2, count = 0;
for (int i = 0; i <= USHRT_MAX; i++) { // Iterate over histogram to find the med
count += histo[i];
if (count >= medianPos) { medianValMSW = i; break; }
}
if (!(Length % 2 || count > medianPos)) { // If the size is even, find the next
Если условие сработало, то на втором проходе просто смотрим минимум и максимум:
if (!(Length % 2 || count > medianPos)) { // If the size is even, find the next
nextVal = medianValMSW;
while (!histo[++nextVal]);
for (max = 0, min = 65535, i = 0; i < Length; i++) {
indexMSW = (ptr[i] & 0xFFFF0000) >> 16;
if (medianValMSW == indexMSW && (ptr[i] & 0x0000FFFF) > max)
max = (ptr[i] & 0x0000FFFF);
if (indexMSW == nextVal && (ptr[i] & 0x0000FFFF) < min)
min = (ptr[i] & 0x0000FFFF);
}
medianLeft = (medianValMSW << 16) | max;
medianRight = (nextVal << 16) | min;
*med = ((double)medianLeft + (double)medianRight) / 2.0;
А если условие не сработало, то сбрасываем гистограмму и делаем второй проход по младшему слову вот так, занося в гистограмму только те значения у которых старшее слово равно найденному на первом проходе и попутно считая количество элементов слева:
ZeroMemory(histo, (USHRT_MAX + 1) * sizeof(size_t));
med_ = medianValMSW << 16;
for (count = 0, i = 0; i < Length; i++) {
indexMSW = (ptr[i] & 0xFFFF0000) >> 16;
if (medianValMSW == indexMSW) histo[(ptr[i] & 0x0000FFFF)]++;
if (ptr[i] < med_) count++;
}
// Find the median position;
medianValLSW = 0;
for (int i = 0; i <= USHRT_MAX; i++) { // Iterate over histogram
count += histo[i];
if (count >= medianPos) { medianValLSW = i; break; }
}
Ну и здесь нас может настигнуть такая же ситуация, когда либо медиана собирается из двух значений, либо из одного:
if (!(Length % 2 || count > medianPos)) {
nextVal = medianValLSW;
while (!histo[++nextVal]);
medianLeft = (medianValMSW << 16) | medianValLSW;
medianRight = (medianValMSW << 16) | nextVal;
*med = ((double)medianLeft + (double)medianRight) / 2.0;
}
else {
medianValI32 = (medianValMSW << 16) | medianValLSW;
*med = (double)medianValI32;
}
Вот, собственно и всё. Понятно, что метод будет работать и для 64-х битных массивов, просто пройти по массиву придётся четыре раза, поскольку у нас четыре слова по два байта, причём частный случай с разными значениями слева и справа при чётном количестве элементов может возникнуть на любом прогоне.
полный листинг MedianU32
LIBMED_API int MedianU32(unsigned int* ptr, size_t Length, double* med)
{
size_t* histo;
int i;
uint64_t medianLeft, medianRight, indexMSW, nextVal, med_;
uint64_t medianValI32, medianValLSW, medianValMSW = 0, min, max;
if (!ptr || !Length) return -1;
histo = (size_t*)calloc(USHRT_MAX + 1, sizeof(size_t));
if (!histo) return -2;
//MSW HISTO:
for (int i = 0; i < Length; i++) histo[(ptr[i] & 0xFFFF0000) >> 16]++;
// Find the median position;
uint64_t medianPos = (Length + 1) / 2, count = 0;
for (int i = 0; i <= USHRT_MAX; i++) { // Iterate over histogram to find the med
count += histo[i];
if (count >= medianPos) { medianValMSW = i; break; }
}
if (!(Length % 2 || count > medianPos)) { // If the size is even, find the next
nextVal = medianValMSW;
while (!histo[++nextVal]);
for (max = 0, min = 65535, i = 0; i < Length; i++) {
indexMSW = (ptr[i] & 0xFFFF0000) >> 16;
if (medianValMSW == indexMSW && (ptr[i] & 0x0000FFFF) > max)
max = (ptr[i] & 0x0000FFFF);
if (indexMSW == nextVal && (ptr[i] & 0x0000FFFF) < min)
min = (ptr[i] & 0x0000FFFF);
}
medianLeft = (medianValMSW << 16) | max;
medianRight = (nextVal << 16) | min;
*med = ((double)medianLeft + (double)medianRight) / 2.0;
}
else { //LSW HISTO
ZeroMemory(histo, (USHRT_MAX + 1) * sizeof(size_t));
med_ = medianValMSW << 16;
for (count = 0, i = 0; i < Length; i++) {
indexMSW = (ptr[i] & 0xFFFF0000) >> 16;
if (medianValMSW == indexMSW) histo[(ptr[i] & 0x0000FFFF)]++;
if (ptr[i] < med_) count++;
}
// Find the median position;
medianValLSW = 0;
for (int i = 0; i <= USHRT_MAX; i++) { // Iterate over histogram
count += histo[i];
if (count >= medianPos) { medianValLSW = i; break; }
}
if (!(Length % 2 || count > medianPos)) {
nextVal = medianValLSW;
while (!histo[++nextVal]);
medianLeft = (medianValMSW << 16) | medianValLSW;
medianRight = (medianValMSW << 16) | nextVal;
*med = ((double)medianLeft + (double)medianRight) / 2.0;
}
else {
medianValI32 = (medianValMSW << 16) | medianValLSW;
*med = (double)medianValI32;
}
}
free(histo);
return 0;
} //MedianU32
Double
Но внутренний голос не отставал — ведь есть же ещё числа с плавающей точкой, так что код этот для беззнаковых 32-х битных целых я дотошно не проверял, поскольку у меня зачесались руки проделать такой же фокус для чисел с плавающей запятой, причём двойной точности и со знаком, ведь если взглянуть на представление IEEE 754, которым мы пользуемся, то легко заметить, что в положительной области монотонно возрастающим числам на шкале с плавающей точкой соответствуют монотонно возрастающие целые числа в том же битовом представлении, то есть если просто работать с этим массивом как с массивом целых (той же разрядности), а потом перевести представление обратно, то мы получим истинное значение медианы.
Вот смотрите на примере одинарной точности:
Нуль он так и будет нуль.
Если мы выставим первый бит, то получим наименьшее позитивное число:
1(0000 0001)->1,4012984643248171E-45
следующее вот такое
2(0000 0002)->2,8025969286496341E-45
...
65535(0000 FFFF)->9,1834094859526886E-41
65536(0001 0000)->9,1835496157991211E-41
...
Вот на этом значении (выставив 23-й бит) мы достигаем точной единицы:
1065353216(3F80 0000)->1,000000000000000000
... и далее до максимума:
2139095039(7F7F FFFF)->3,4028234663852886E+38
2139095040(7F80 0000)->Inf
2139095041(7F80 0001)->NaN
... едем дальше
2147483647(7FFF FFFF)->NaN
А вот при старшем бите мы уходим в негативные значения:
2147483648(8000 0000)->-0
2147483649(8000 0001)->-1,4012984643248171E-45
2147483650(8000 0002)->-2,8025969286496341E-45
3212836864(BF80 0000)->-1
4286578687(FF7F FFFF)->-3,4028234663852886E+38
4286578688(FF80 0000)->-Inf
4286578689(FF80 0001)->NaN
...
Остаётся лишь последний вопрос — как обойтись с негативными значениями? Если мы заранее знаем, что негативных значений в исходном массиве не будет, то никаких дополнительных телодвижений делать не нужно — всё будет работать как с беззнаковыми целыми. А вот если нет, то нам нужно сбросить старший бит у негативных значений, и установить его у позитивных значений (что сдвинет их вправо по беззнаковой шкале), но при этом также "перевернуть" всю последовательность негативных, чтобы меньшие числа располагались левее больших. Вот что я имею ввиду:

Вот теперь во всём диапазоне значений старшее слово будет монотонно расти и гистограмма будет работать (в принципе есть разные способы достичь этого результата, мне показалось проще вот так).
Итак, будем пилить вот такую функцию:
LIBMED_API int MedianDBL(double* ptr, size_t Length, double* med)
Гистограмма будет по-прежнему 64К элементов:
size_t* histo = (size_t*)calloc(USHRT_MAX + 1, sizeof(size_t));
Самое главное - берём указатель на входной массив и говорим, что работать будем с целыми:
uint64_t* ptr_U64 = (uint64_t*)ptr; //Cast
Чтобы у меня не рябило в глазах от нулей, сделаю несколько "упрощающих" подмен, да простят меня все, кто будет править этот код после меня:
#define xFFFF 0xFFFFFFFFFFFFFFFF
#define x8000 0x8000000000000000
#define x0000 0x0000000000000000
#define xF000 0xFFFF000000000000
#define x0F00 0x0000FFFF00000000
#define x00F0 0x00000000FFFF0000
#define x000F 0x000000000000FFFF
//0 - LSW; 3 - MSW
#define W3 (ptr_U64[i] & 0xFFFF000000000000)
#define W2 (ptr_U64[i] & 0x0000FFFF00000000)
#define W1 (ptr_U64[i] & 0x00000000FFFF0000)
#define W0 (ptr_U64[i] & 0x000000000000FFFF)
Ещё мне понадобятся простенькие энкодер и декодер:
#define ENCODE(var) if (!((var) & x8000)) (var) ^= x8000; else (var) ^= xFFFF
#define DECODE(var) if (((var) & x8000)) (var) ^= x8000; else (var) ^= xFFFF
Энкодер будет инвертировать старший бит, если он не установлен, в противном случае инвертировать вообще всё. Декодер будет возвращать всё обратно.
Делаем первый проход - готовим данные и собираем гистограмму из старшего слова:
for (i = 0; i < Length; i++) {
ENCODE(ptr_U64[i]);
histo[W3 >> 48]++;
}
Менять входные данные в общем — ну так себе идея, но мы в конце потихоньку вернём всё обратно, авось никто не заметит (до тех пор пока никто не будет читать этот массив во время выполнения). У numpy, кстати, я видел флаг overwrite_input — можно или нет модифицировать входящий массив.
Делаем первый проход по гистограмме, останавливаемся, когда наберём половину:
medianPos = (Length + 1) / 2;
for (count = 0, i = 0; i <= USHRT_MAX; i++) { // Iterate over histogram
count += histo[i];
if (count >= medianPos) { medValW3 = i; break; } // >> single Median at MSW
}
В случае чётного количества элементов и точного совпадения проматываем до следующего значения:
if (!(Length & 1) && count == medianPos) { //W3
nextVal = medValW3;
while (!histo[++nextVal]);
medValW3 <<= 48; nextVal <<= 48;
Теперь второй проход: ищем минимум и максимум во втором слове, там, где старшее совпадает с найденными выше:
for (max2 = 0, min2 = _UI64_MAX, i = 0; i < Length; i++) { //1.2 pass
if (medValW3 == W3 && W2 > max2) max2 = W2;
if (W3 == nextVal && W2 < min2) min2 = W2;
}
Повторяем для двух оставшихся слов
for (max1 = 0, min1 = _UI64_MAX, i = 0; i < Length; i++) { //1.3 pass
if (medValW3 == W3 && max2 == W2 && W1 > max1) max1 = W1;
if (W3 == nextVal && min2 == W2 && W1 < min1) min1 = W1;
}
for (max0 = 0, min0 = _UI64_MAX, i = 0; i < Length; i++) { //1.4 pass, final
if (medValW3 == W3 && max2 == W2 && max1 == W1 && W0 > max0) max0 = W0;
if (W3 == nextVal && min2 == W2 && min1 == W1 && W0 < min0) min0 = W0;
DECODE(ptr_U64[i]);
} // 1.2 - 1.4
В конце не забываем вернуть массив в исходное состояние.
Ну и "собираем" медиану из двух частей:
medianLeft = medValW3 | max2 | max1 | max0;
medianRight = nextVal | min2 | min1 | min0;
DECODE(medianLeft); DECODE(medianRight);
*med = (*(double*)&medianLeft + *(double*)&medianRight) / 2.0;
А в случае нечётного количества элементов собираем следующую гистограмму:
memset(histo, 0, (USHRT_MAX + 1) * sizeof(size_t));
med_ = (medValW3 <<= 48);
for (count = 0, i = 0; i < Length; i++) { //2.2 pass
if (medValW3 == W3) histo[W2 >> 32]++;
if (ptr_U64[i] < med_) count++;
} // 2.2
for (int i = 0; i <= USHRT_MAX; i++) {
count += histo[i]; //continue
if (count >= medianPos) { medValW2 = i; break; }
}
Ну и так далее, теперь собираем всё вместе методом отчаянного копипастинга (я отнюдь не случайно добавил хаб "ненормальное программирование"):
полный листинг MedianDBL
#define xFFFF 0xFFFFFFFFFFFFFFFF
#define x8000 0x8000000000000000
#define x0000 0x0000000000000000
#define xF000 0xFFFF000000000000
#define x0F00 0x0000FFFF00000000
#define x00F0 0x00000000FFFF0000
#define x000F 0x000000000000FFFF
//0 - LSW; 3 - MSW
#define W3 (ptr_U64[i] & 0xFFFF000000000000)
#define W2 (ptr_U64[i] & 0x0000FFFF00000000)
#define W1 (ptr_U64[i] & 0x00000000FFFF0000)
#define W0 (ptr_U64[i] & 0x000000000000FFFF)
#define ENCODE(var) if (!((var) & x8000)) (var) ^= x8000; else (var) ^= xFFFF
#define DECODE(var) if (((var) & x8000)) (var) ^= x8000; else (var) ^= xFFFF
LIBMED_API int MedianDBL(double* ptr, size_t Length, double* med)
{
if (!ptr || !Length) return -1;
size_t* histo = (size_t*)calloc(USHRT_MAX + 1, sizeof(size_t));
if (!histo) return -2;
uint64_t count, i, medianPos;
uint64_t min0, min1, min2, max0, max1, max2;
uint64_t medValW0 = 0, medValW1 = 0, medValW2 = 0, medValW3 = 0;
uint64_t medianLeft, medianRight, medVal, nextVal, med_;
uint64_t* ptr_U64 = (uint64_t*)ptr; //Cast
for (i = 0; i < Length; i++) {
ENCODE(ptr_U64[i]);
histo[W3 >> 48]++;
}
// Find the initial median position;
medianPos = (Length + 1) / 2;
for (count = 0, i = 0; i <= USHRT_MAX; i++) { // Iterate over histogram
count += histo[i];
if (count >= medianPos) { medValW3 = i; break; } // >> single Median at MSW
}
if (!(Length & 1) && count == medianPos) { //W3
nextVal = medValW3;
while (!histo[++nextVal]);
medValW3 <<= 48; nextVal <<= 48;
for (max2 = 0, min2 = _UI64_MAX, i = 0; i < Length; i++) { //1.2 pass
if (medValW3 == W3 && W2 > max2) max2 = W2;
if (W3 == nextVal && W2 < min2) min2 = W2;
}
for (max1 = 0, min1 = _UI64_MAX, i = 0; i < Length; i++) { //1.3 pass
if (medValW3 == W3 && max2 == W2 && W1 > max1) max1 = W1;
if (W3 == nextVal && min2 == W2 && W1 < min1) min1 = W1;
}
for (max0 = 0, min0 = _UI64_MAX, i = 0; i < Length; i++) { //1.4 pass, final
if (medValW3 == W3 && max2 == W2 && max1 == W1 && W0 > max0) max0 = W0;
if (W3 == nextVal && min2 == W2 && min1 == W1 && W0 < min0) min0 = W0;
DECODE(ptr_U64[i]);
} // 1.2 - 1.4
medianLeft = medValW3 | max2 | max1 | max0;
DECODE(medianLeft);
medianRight = nextVal | min2 | min1 | min0;
DECODE(medianRight);
*med = (*(double*)&medianLeft + *(double*)&medianRight) / 2.0;
} else {
memset(histo, 0, (USHRT_MAX + 1) * sizeof(size_t));
med_ = (medValW3 <<= 48);
for (count = 0, i = 0; i < Length; i++) { //2.2 pass
if (medValW3 == W3) histo[W2 >> 32]++;
if (ptr_U64[i] < med_) count++;
} // 2.2
for (int i = 0; i <= USHRT_MAX; i++) {
count += histo[i]; //continue
if (count >= medianPos) { medValW2 = i; break; }
}
if (!(Length & 1) && count == medianPos) { // W2
nextVal = medValW2;
while (!histo[++nextVal]);
medValW2 <<= 32;
nextVal <<= 32;
for (max1 = 0, min1 = _UI64_MAX, i = 0; i < Length; i++) { //2.3 pass
if (medValW3 == W3 && medValW2 == W2 && W1 > max1) max1 = W1;
if (W3 == medValW3 && nextVal == W2 && W1 < min1) min1 = W1;
}
for (max0 = 0, min0 = _UI64_MAX, i = 0; i < Length; i++) { //2.4 pass, final
if (medValW3 == W3 && medValW2 == W2 && max1 == W1 && W0 > max0) max0 = W0;
if (W3 == medValW3 && nextVal == W2 && min1 == W1 && W0 < min0) min0 = W0;
DECODE(ptr_U64[i]);
} //2.3-2.4
medianLeft = medValW3 | medValW2 | max1 | max0;
DECODE(medianLeft);
medianRight = medValW3 | nextVal | min1 | min0;
DECODE(medianRight);
*med = (*(double*)&medianLeft + *(double*)&medianRight) / 2.0;
} else {
memset(histo, 0, (USHRT_MAX + 1) * sizeof(size_t));
med_ = medValW3 | (medValW2 <<= 32);
for (count = 0, i = 0; i < Length; i++) { //3.3 pass
if (medValW3 == W3 && medValW2 == W2) histo[W1 >> 16]++;
if (ptr_U64[i] < med_) count++;
} //3.3
for (int i = 0; i <= USHRT_MAX; i++) {
count += histo[i];
if (count >= medianPos) { medValW1 = i; break; }
}
if (!(Length & 1) && count == medianPos) { //W1
nextVal = medValW1;
while (!histo[++nextVal]);
medValW1 <<= 16;
nextVal <<= 16;
for (max0 = 0, min0 = _UI64_MAX, i = 0; i < Length; i++) { //3.4 pass, final
if ((medValW3 == W3) && (medValW2 == W2) && (medValW1 == W1) && W0 > max0) max0 = W0;
if ((W3 == medValW3) && (medValW2 == W2) && (nextVal == W1) && W0 < min0) min0 = W0;
DECODE(ptr_U64[i]);
} //3.4
medianLeft = medValW3 | medValW2 | medValW1 | max0;
DECODE(medianLeft);
medianRight = medValW3 | medValW2 | nextVal | min0;
DECODE(medianRight);
*med = (*(double*)&medianLeft + *(double*)&medianRight) / 2.0;
} else {
memset(histo, 0, (USHRT_MAX + 1) * sizeof(size_t));
med_ = medValW3 | medValW2 | (medValW1 <<= 16);
for (count = 0, i = 0; i < Length; i++) {//!! Spaziergang !!
if (medValW3 == W3 && medValW2 == W2 && medValW1 == W1) histo[W0]++;
if (ptr_U64[i] < med_) count++;
DECODE(ptr_U64[i]); //restore back
} //4.4, final
for (int i = 0; i <= USHRT_MAX; i++) {
count += histo[i];
if (count >= medianPos) { medValW0 = i; break; }
}
if (!(Length & 1) && count == medianPos) {
nextVal = medValW0;
while (!histo[++nextVal]);
medianLeft = medValW3 | medValW2 | medValW1 | medValW0;
DECODE(medianLeft);
medianRight = medValW3 | medValW2 | medValW1 | nextVal;
DECODE(medianRight);
*med = (*(double*)&medianLeft + *(double*)&medianRight) / 2.0;
} else {
medVal = medValW3 | medValW2 | medValW1 | medValW0;
DECODE(medVal);
*med = *(double*)&medVal;
}
}
}
}
free(histo);
return 0;
} //MedianDBL
Выглядит довольно сурово, но если сравнить этот код с "классикой" типа QuickSelect из "Численных методов", то в предложенном подходе многое даже проще. И да, я учил Си по Кернигану и Ритчи.
Производительность
Ну вот, теперь можно и погонять этот код и сравнить с другими реализациями.
У меня в руках есть функции вычисления медиан из двух библиотеки - одна это Numpy Median, а вторая - NI Median.
Вот с ними мы и будем соревноваться.
Начну я с Питона, пожалуй, в силу значительно большей распространённости (продукты NI - используются не так часто). Я оформлю этот код выше библиотечкой libMed.dll и вызову из Питона вот так (я ни разу не профи в Питоне, и вызываю DLL из него в первый раз в жизни, так что получилось как получилось):
import os
from random import random
from time import time
from ctypes import CDLL, POINTER, byref, c_size_t, c_double
mylib = CDLL(os.path.dirname(os.path.abspath(__file__)) + os.path.sep + "libMed.dll")
ND_POINTER_1 = np.ctypeslib.ndpointer(dtype=np.float64, ndim=1, flags="C")
mylib.fnMedian.argtypes = [ND_POINTER_1, c_size_t, POINTER( c_double )]
mylib.fnMedian.restype = np.int32
# Test Data
T1M = np.array([random() for _ in range(1024*1024)])
MyRes = c_double( 0.0 )
start = time()
mylib.fnMedian(T1M, T1M.size, byref(MyRes))
print ("My 1M:", (time() - start)*1000, "ms; res = ", MyRes)
#...
(где-то вы будете встречать имя fnMedian, а не MedianDBL, это я просто декорацию имён выключил, да так оно и осталось).
Я в курсе невысокой точности time(), но мне и не нужно гнаться за микросекундами, в конце концов я могу прокрутить код десяток раз да получить среднее. Я проверю на трёх самых "ходовых" (в моём частном случае) размерах картинок — 1024х1024, 2048х2048 и 4096х4096, ну то есть 1, 4 и 16 миллионов случайных значений в массиве.
полный листинг теста производительности
import os
import numpy as np
from random import random
from time import time
from ctypes import CDLL, POINTER, byref, c_size_t, c_double
mylib = CDLL(os.path.dirname(os.path.abspath(__file__)) + os.path.sep + "libMed.dll")
ND_POINTER_1 = np.ctypeslib.ndpointer(dtype=np.float64, ndim=1, flags="C")
mylib.fastMedian.argtypes = [ND_POINTER_1, c_size_t, POINTER( c_double )]
mylib.fastMedian.restype = np.int32
# Test Data
T1M = np.array([random() for _ in range(1024*1024+1)])
T4M = np.array([random() for _ in range(2048*2048+1)])
T16M = np.array([random() for _ in range(4096*4096+1)])
MyRes = c_double( 0.0 )
start = time()
for x in range(10):mylib.fastMedian(T1M, T1M.size, byref(MyRes))
print ("My 1M:", (time() - start)*100, "ms; res = ", MyRes)
start = time()
for x in range(10):NumpyRes = np.median(T1M)
print ("np 1M:", (time() - start)*100, "ms; res = ", NumpyRes)
if (MyRes == NumpyRes): print("passed")
start = time()
for x in range(10):mylib.fastMedian(T4M, T4M.size, byref(MyRes))
print ("My 4M:", (time() - start)*100, "ms; res = ", MyRes)
start = time()
for x in range(10):NumpyRes = np.median(T4M)
print ("np 4M:", (time() - start)*100, "ms; res = ", NumpyRes)
if (MyRes == NumpyRes): print("passed")
start = time()
for x in range(10):mylib.fastMedian(T16M, T16M.size, byref(MyRes))
print ("My 16M:", (time() - start)*100, "ms; res = ", MyRes)
start = time()
for x in range(10):NumpyRes = np.median(T16M)
print ("np 16M:", (time() - start)*100, "ms; res = ", NumpyRes)
if (MyRes == NumpyRes): print("passed")
Результаты (My - это мой метод, а np — это numpy):
>python fastMedTest.py
My 1M: 9.675335884094238 ms; res = c_double(0.49913991096863186)
np 1M: 17.79000759124756 ms; res = 0.49913991096863186
passed
My 4M: 38.81254196166992 ms; res = c_double(0.5001439678114372)
np 4M: 69.83757019042969 ms; res = 0.5001439678114372
passed
My 16M: 152.37784385681152 ms; res = c_double(0.5000523968034343)
np 16M: 259.2304468154907 ms; res = 0.5000523968034343
passed
В моём Precision M6700, на котором я упражняюсь, камушек i7-3740QM, поэтому результаты так себе. А ноут, кстати, считаю одним из лучших всех времён (впереди только отдельные ThinkPadы), если б не вес под четыре кило.
Если пересесть на i7-7700 посвежее, то станет чуть веселее:
>python fastMedTest.py
My 1M: 4.303789138793945 ms; res = c_double(0.5003872509309095)
np 1M: 10.99863052368164 ms; res = 0.5003872509309095
passed
My 4M: 18.0020809173584 ms; res = c_double(0.4999627738635442)
np 4M: 46.71292304992676 ms; res = 0.4999627738635442
passed
My 16M: 78.09562683105469 ms; res = c_double(0.5001147029114446)
np 16M: 167.00820922851562 ms; res = 0.5001147029114446
passed
Но в любом случае в наличии практически двукратный выигрыш по времени, при этом результат в точности совпадает. В случае, когда данные будут содержать только положительные числа, а тем более в случае одинарной точности (когда мы найдём медиану всего за два прохода) выигрыш будут ещё значительнее. Эту же библиотеку я могу и из LabVIEW вызвать и проверить результат и время:

Библиотека от NI даёт примерно похожие с numpy результаты. В принципе начиная с LabVIEW 2019 нам завезли поддержку Питона прямо в LabVIEW и я могу вызвать Медиану из numpy вот так:

Но для оценки производительности это не очень подходит, поскольку я вижу очень сильные задержки при пробросе LabVIEW массива в скрипт на Питоне.
В принципе там есть ещё что пооптимизировать, часть можно переписать на AVX2/AVX512, возможно, Интеловский компилятор сможет дать чуть большую производительность. Разумеется, выигрыш этот метод даст начиная с определённого размера массива, так как прогулки по гистограммам сами по себе не бесплатны, и до 10000-15000 элементов он будет медленнее, кроме того довольно сильно зависеть от входных данных. Но в принципе уже с размеров в половину гистограммы, где-то с 25000 элементов - прирост производительности заметен:
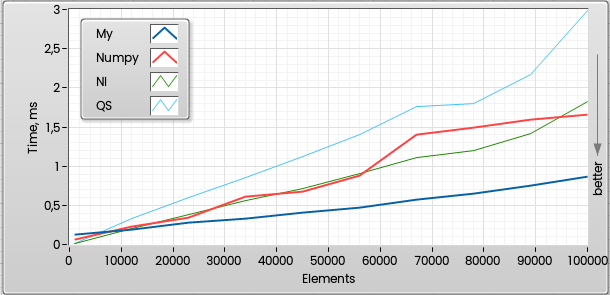
(QS - это Quick Select из "Численных Методов"). А это график до миллиона элементов. Видно. что NI и Numpy бегут почти вровень (numpy чуть лучше), а предложенный метод уверенно лидирует (чем больше массив, тем меньше вклад от пробежек по гистограммам):

Вот собственно и всё. Код (использовалась Студия 2022 версии 17.7.6) лежит на гитхабе, если кому нужно.
Если я где-либо ошибся, либо таки изобрёл велосипед — не сочтите за труд, напишите, пожалуйста в комментах.
Всем добра!
Комментарии (16)

chernish2
31.10.2023 16:21В OpenCV нет метода вычисления медианы? Вы серьезно?

AndreyDmitriev Автор
31.10.2023 16:21+4Абсолютно серьёзно. Есть медианная фильтрация, а вот просто значения медианы по каналу — нет. Все изобретают велосипед либо через cv::calcHist (), либо как я, ну или средним вместо медианы обходятся.Я по исходникам 4.8.1 поискал как Median так и NthOrder, но правда не нашёл.

alcotel
31.10.2023 16:21+1Весьма круто!
Заметно, что похоже на шаг корзинной сортировки. А он, как раз что-то типа O(n).Ну, на самом деле у вас O(n*log(d)), где log(d) - это разрядность данных, а d - количество этих самых корзин. Вы же при увеличении разрядности таки увеличиваете количество проходов по исходному массиву, чтобы гистограмма помещалась в кэш)
Это для большой разрядности, конечно, или для какой-то универсальной библиотеки обработки даблов. В задачах обработки сигналов не видел, чтобы АЦП выдавало больше 16 бит с аццкой скоростью. 24 бит - скорость уже точно не аццкая, и потребности в медиане не видел.
Ну и смачный подход к обработке данных с плавающей точкой, как с целыми - достойно! Это почти как idSoftware с квадратным корнем. ЦП на десктопах и сейчас с целыми работают раза в 4 быстрее, чем с FP. А вот GPU - не уверен.

AndreyDmitriev Автор
31.10.2023 16:21Спасибо! Если разрядность данных учитывать, то, конечно, асимптотика будет ещё хуже — там ведь не только больше проходов, но и больше сравнений потребуется. Но я всё-таки за сложность от количества данных, а не от типа. Практически же это действительно не так часто бывает нужно, да и отсутствие функции вычисления медианы в трёх библиотеках обработки изображений как бы намекает. Но если у кого-то медиана - "бутылочное горлышко", то как вариант.

U235a
31.10.2023 16:21Здорово, но не думаю, что окончалельный результат (ради чего все и делается) сильно бы изменился, если для нахождения медианы предварительно перевести float в int8. Будет ли в формуле медиана, 49 или 51 процентиль, скорее всего ничего особо не поменяется.Нужна ли такая точность как сейчас?

AndreyDmitriev Автор
31.10.2023 16:21Требуемая точность в общем от задачи зависит; если отрезать младший байт от float, то по моим прикидкам мы потеряем что-то около сотой процента в точности. Можно даже два байта отчекрыжить, тогда потеряем всего-то около процента. Но если оставить только один байт, то потеря будет значительна - ведь у нас в распоряжении будет всего 256 значений на весь диапазон. В данном же случае интерес был более "спортивный", нежели прикладной — получить ровно тот же результат, что выдают пара других библиотечных функций, но за меньшее время.

alcotel
31.10.2023 16:21Результат изменится. Все данные могут быть одного порядка, и тогда int8 будет один и тот-же, и все попадут в одну точку гистограммы. Или наоборот - при большом разбросе все попадут в две крайние точки.
Чтобы так легко сворачивать исходные данные, нужно про них что-то знать. А это как минимум ещё один проход по ним.

speshuric
31.10.2023 16:21+1А я правильно понимаю, что NaN ваша реализация не совсем дружит?

AndreyDmitriev Автор
31.10.2023 16:21+1Это хороший вопрос. Да, не совсем, если во входном массиве все элементы будут NaN, то сработает, а вот если перемешаны с "нормальными" — то нет (точнее не всегда). Я проверил как реагирует на NaN "референсная" NI реализация - там если хотя бы одно число NaN, то и результат всегда NaN, что в общем логично. Это просто элементарная проверка на первом прогоне, и она не должна сильно просадить производительность. Я добавлю, пожалуй, как только время появится. А с плюс минус бесконечностями вроде дружит.

speshuric
31.10.2023 16:21То что поправить несложно - это понятно. Я просто обратил внимание, что этот момент не обработан.


MzMz
я не очень понял из статьи - а что именно мешает просто отсортировать данные за O(n*log(n)) вместо построения гистограммы?
AndreyDmitriev Автор
Да как бы ничто не мешает, но сложности (n*log(n)) именно и хочется избежать. Исходные данные изначально несортированны, разумеется. А так сложность остаётся линейной, нам хочется детерминированного O(n). Ну и любой алгоритм поиска медианы, основанный на сортировке просядет по производительности на больших массивах. Это вот здесь уже обсуждалось немножко - Мой любимый алгоритм: нахождение медианы за линейное время
elderos
сортировать-то не надо, можно quickselect с O(N) в среднем
AndreyDmitriev Автор
Это так, просто по моим наблюдениям классический quickselect в среднем примерно этак вдвое-втрое медленнее гистограммного метода. Собственно в nimpy вариации на тему quickselect и реализованы в selection.cpp И там и там линейное время, но общий наклон линии тоже хотелось бы уменьшить. Это больше не про теоретическую сложность, а про практическое время выполнения на данном наборе данных.
elderos
я думаю в нумпи просто не рассчитывали на читерскую гистограмму на 2^16 бакетов :-) оптимизация на конкретные данные она такая
она же кажется и слабое звено, потому что на массивах в 100 элементов будет только тормозить
впрочем, если продолжить мысль то получится эдакий radixselect, прикольно
че если брать по 8 бит например? и нельзя ли как-то заюзать simd
AndreyDmitriev Автор
Про 8 бит я думал, но необходимость увеличенного вдвое количества проходов прибьёт идею, особенно если исходный массив в кэш не влезет — память, она медленная очень, кроме того чем дальше спускаться к младшим байтам, тем больше сравнений. Simd заюзать можно, но там очень много времени положить придётся. Простое включение AVX2 ничего не даёт - это я проверил, впрочем ассемблеровский листинг не смотрел. Проще вначале взять интеловский компилятор и посмотреть, что там векторизатор скажет.