Кратко:
В оригинальном исследовании показано совсем не то, что люди думают.
Оригинальное исследование так криво сделано статистически, что просто не удовлетворяет критерию фальсифицируемости. Простыми словами — генератор случайных чисел демонстрирует такой же результат.
Единственное, что этот эффект демонстрирует — это любовь людей к красивым историям (а математику никто не любит … и вообще есть ложь, большая ложь и статистика).
Существующие статьи на Хабре
Я решил, что не могу не писать после прочтения вот этого поста. Автор почему‑то пишет про автокорреляцию, но понимает под этим что‑то своё и в целом пост оценен в комментариях критически. Автокорреляция — это термин относящийся к последовательным (чаще всего временным) рядам и к делу отношения не имеет.
Далее я поискал, что ещё писали на Хабре в последнее время. И тут я приуныл.
Просто посты по поводу эффекта Даннинга‑Крюгера (далее эффект Д‑К):
Попытки критики:
Эффект Даннинга‑Крюгера — не то, чем кажется или Почему деление на умных и глупых — само по себе глупость Тут суть претензий психологическая. Людям нравится этот эффект и это тоже пример когнитивного искажения. По сути это тоже поддерживающий пост.
Разоблачаем Эффект Даннинга‑Крюгера. Статистический артефакт, пример автокорреляции — тут ад с автокорреляцией и ничего не понятно.
Чем является и чем не является эффект Даннинга‑Крюгера — адекватная статья, но слишком краткая и видимо никто ничего не понял.
Я‑то думал стюардессу уже закопали… Придется самому.
Расхождение исследования и интерпретации
«Долину отчаяния» по факту выдумали. Самооценка в исследовании строго растёт с результатом тестов. Коэффициент в регрессии сильно ниже единицы и поэтому можно разводить рассуждения об относительной пере‑ и недо‑оценке в сравнении с реальным результатом теста.
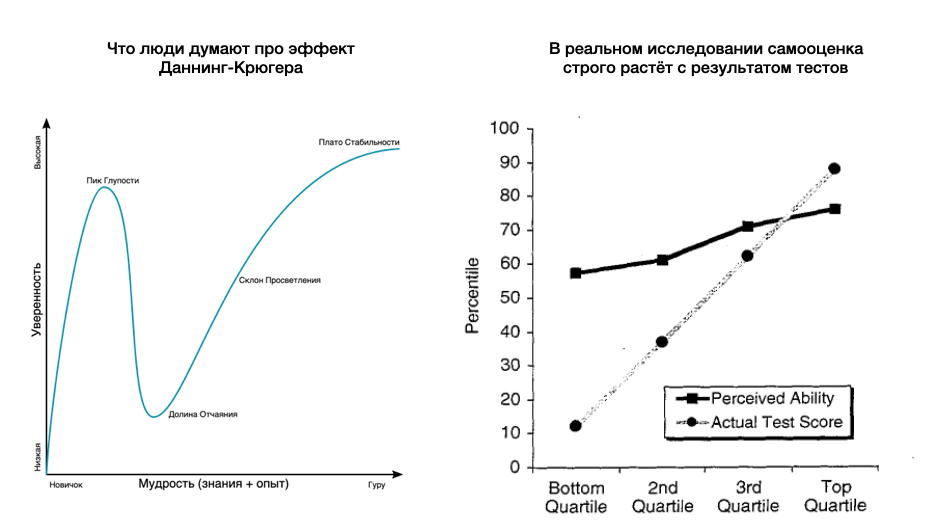
Источники для коллажа: Даннинг и Крюгер (1999) и Даннинг с Крюгером, Сократ и круги знаний.
Нефальсифицируемость всего исследования
Критиковать оригинальное исследование с точки зрения статистики стали довольно быстро. Первый хороший разбор вышел через три года у Krueger and Mueller (2002). Но кому нужны факты, когда такая тема для графоманства пропадает.
В эксперименте по сути сравниваются два метода измерения неких способностей:
Через тест
Через само‑оценку
Если оба метода работают нормально и без искажений, но имеют некую погрешность (самую нейтральную — просто нормально распределённый шум), то мы чисто математически должны получить коэффициент регрессии ниже единицы. Это явление называется регрессия к среднему (Regression toward the mean) и известно уже более ста лет.
Отступление - откуда есть пошло слово регрессия
В 1889 году Френсис Гальтон построил график зависимости роста сыновей от роста отцов. И получил коэффициент регрессии в районе 2/3. То есть сыновья очень низких отцов были выше, а сыновья очень высоких отцов были ниже (ничего не напоминает?). Гальтон использовал термин регрессия (в смысле роста у следующих поколений) и так этот термин вошёл в статистику. Сегодня все знают про регрессию, а вот про «регрессию к среднему» знают единицы.

Источник: википедия — Regression toward the mean
Назад к нашему эффекту Д‑К. Само наличие погрешности в двух измерениях уже гарантирует, что коэффициент будет ниже единицы.
То есть, если бы вместо вопроса про самооценку был просто другого типа тест на ту же способность, то мы бы получили похожий результат — испытуемые хорошо справляющиеся с тестом А относительно хуже справляются с тестом Б и можно начинать писать бестселлер про… психологические причины этой разницы между тестами.
Без формул проще всего объяснить так — лидеры в первом измерении реально сильны + им повезло. А во втором измерении им не повезло и они откатились в середину. И аналогично с худшими результатами.
Никакого нового знания по результатам такого эксперимента мы не получаем. Результат запрограммирован в дизайне — а значит есть проблема с фальсифицируемостью. Либо нужно демонстрировать, что эти тесты имеют низкий уровень шума — проводить повторные измерения всякие и так далее. Я такого не нашёл по факту.
Демонстрирую «эффект» на генераторе случайных чисел
Я ввожу исходный (верный) уровень способностей (нормальное распределение со средним 50 и стандартным отклонением 5) и два раза его «измеряю» прибавляя нормально распределённый шум (среднее 0 и стандартное отклонение 10). Одно измерение можно назвать «тест», а другое «самооценка». Но это только названия.
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
import plotly.express as px
import plotly.graph_objects as go
# Model
df = pd.DataFrame(np.random.normal(50, 5, 500), columns=['underlying_ability'])
df['test'] = df['underlying_ability'] + np.random.normal(0, 10, 500)
df['self_estimate'] = df['underlying_ability'] + np.random.normal(0, 10, 500)
# Fit regression
model = ols("self_estimate ~ test", df).fit()
print(f"self_estimate = {model.params['Intercept']:.2f} + {model.params['test']:.2f}*test")
# Plot data and regression
df['regression'] = model.params['Intercept'] + model.params['test']*df['test']
fig1 = px.scatter(x=df['test'], y=df['self_estimate'])
fig2 = px.line(x=df['test'], y=df['regression'])
fig = fig2.update_traces(line_color='red', line_width=2)
fig = fig = go.Figure(data=fig1.data + fig2.data)
fig.update_layout(
autosize=False,
width=600,
height=600,
plot_bgcolor='rgba(0,0,0,0)'
)Получаем график почти неотличимый от оригинального:
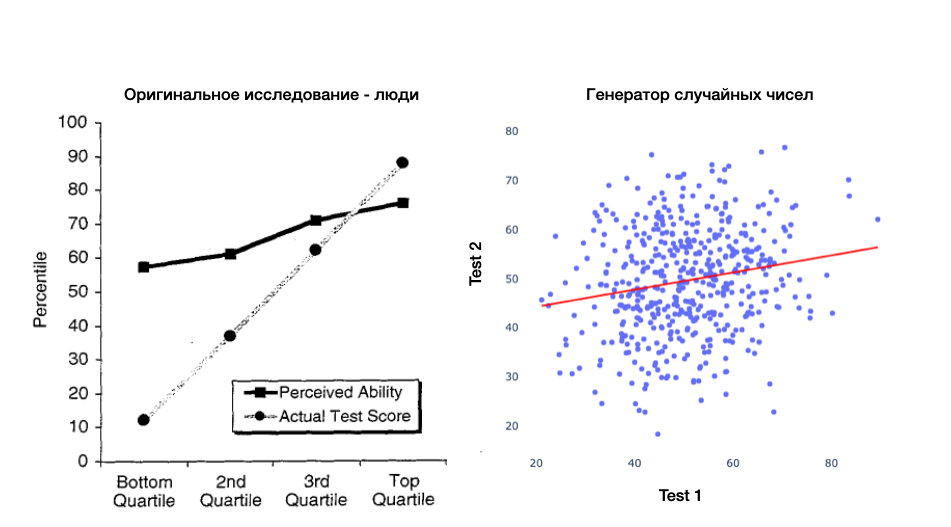
Заметки
Можно заметить, что моя линия регрессии чуть ниже оригинальной (в районе 50, а не 65). Одно из объяснений — это общая склонность завышать свою оценку вне зависимости от способностей. Но я сомневаюсь, что тут есть что‑то важное. Скорее всё зависит от сеттинга для эксперимента. Студентам в опросе могло быть просто стыдно совсем уж низкие баллы писать и сдавать профессору.
Ещё люди копали в сторону ограничений шкалы измерений. Написавшие на 99 из 100 баллов тест по сути могли в самооценке ошибаться только в сторону ниже. И то же самое с худшими студентами. Но мне думается, что это детали. У меня выше получилось неплохо и с нормальным распределением без границ шкалы.
Моё личное мнение по поводу поведенческой психологии как науки
В последнее время эту дисциплину кто только не пинал.
Лет десять назад были обвинения в нереплицируемости (базовая статья Ioannidis 2005) и в p‑hacking (базовая статья Simonsohn U 2014)
В последнее время крупные авторитеты получают обвинения в прямой фабрикации данных — см. Дэн Ариэли (лучше читать hacker news) и Франческа Джино (лучше читать оригинальный разбор). Причём я помню как ещё лет 10 назад над Ариэли в кулуарах другие исследователи прямо ржали. Но про фальшивые данные никто не подозревал.
Уже половину книжки Канемана «Думать быстро и медленно» можно вычёркивать (лучше читать такой разбор).
Что вообще происходит? Далее строго моё мнение.
Неадекватная экстраполяция результатов. Даннинг и Крюгер проводят письменный тест среди студентов‑психологов Корнельского университета на знание английской грамматики, понимание юмора и на умение решать логические задачки. А результаты экстраполируются на все виды знаний и способностей без привязки к письменным тестам и на всех людей подряд в любых ситуациях. Главное чтобы было интересно читать.
Неадекватное описание исследований. На поведение человека влияет куча факторов, которые обычно в статье не описаны. Как и каким тоном давались инструкции? Что в это время было в новостях? Это всё, думаете, не влияет на результат?
Я, помню, работал в опросном бизнесе. Там есть некий протокол как отлавливать интервьюеров, которые рисуют анкеты. Он работает. Но даже после него я всегда строил зависимость результатов от идентификатора интервьюера. И всегда были «звёзды», которые несмотря на инструкцию читать строго формулировку вопроса — «поддерживаете ли Вы…» — умудрялись транслировать своё мнение просто через интонацию. Да, я слушал записи, когда были опросы по телефону.
Как это работает в условиях исследований с двойным ослеплением? У меня есть гипотеза, что многие «эффекты» можно просто разворачивать управляя уровнем внимания респондента. Просто задавая некий фрейм «отвечай быстро не думая» или напротив «думай, тут вопрос с заковыркой». Но проверять я её конечно не буду…
Комментарии (18)

ABRogov
01.12.2023 08:29+4Автор похоже специально разными отступлениями и личными мнениями пытается ее ещё больше запутать и ввести читателя в заблуждение. Формальное доказательство будет?

NNikolay Автор
01.12.2023 08:29Это популярная статья. Если что-то непонятно, то можно попробовать по запускать мой код и почитать по ссылкам. Ссылку на одну академическую статью я дал в самом начале. Там с формулами. Тогда уж можно почитать и ответ на неё от Даннинга с Крюгером и ответ на ответ и... там много было итераций. Можно ещё сходить на английскую википедию, там в соответствующем разделе залинковано таких формальных доказательств штук 10 - ссылка.

ABRogov
01.12.2023 08:29Спасибо за ссылку на википедию, но в каком разделе там перечислены опровержения?
Ссылку на одну академическую статью я дал в самом начале.
Там много ссылок, "ад с автокорреляцией" ?

NNikolay Автор
01.12.2023 08:29Я дал ссылку именно что на раздел википедии, где "перечислены опровержения". Ссылка поломалась? У меня работает.
Не, я про академические статьи в научных журналах, не про хабр. Вот ещё раз - Krueger and Mueller (2002).

adeshere
01.12.2023 08:29+3Когда в обоих переменных есть шум, то правильнее использовать
ортогональную регрессию, а не линейную
В обоих случаях минимизируется сумма квадратов расстояний от экспериментальных точек до аппроксимирующей прямой, поэтому обе эти регрессии, вообще говоря, линейные. А разница в том, что это расстояние берется либо по перпендикуляру к прямой (ортогональная линейная регрессия) либо по вертикали (классическая линейная регрессия, или "просто линейная")
С философской точки зрения, простую линейную регрессию надо использовать, когда независимая переменная известна точно (а зависимая - с ошибками). А ортогональную - когда погрешность (шум) есть в обоих сопоставляемых переменных. Меня обескураживает тот факт, что даже в ВУЗ-ах, рассказывая про регрессионный анализ, преподаватели не всегда акцентируют на этом внимание. Хотя тут вообще никаких формул нет - просто элементарная философия, понятная "из первых принципов"
Тогда
смещение коэффициента регрессии, вызванное зашумлением, исчезает
Вот сварганил наспех на коленке иллюстрацию - пояснение:
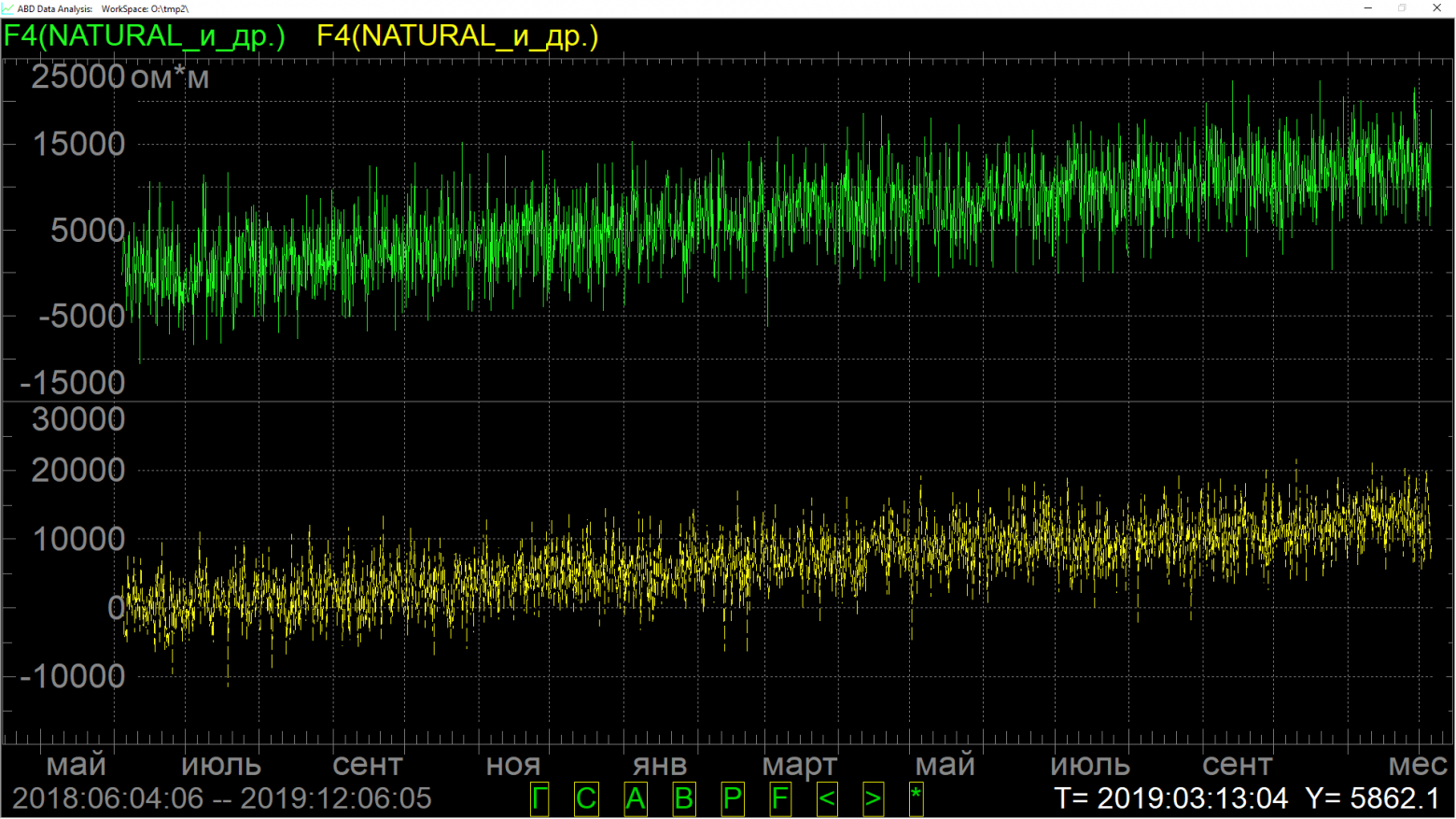
К одному и тому же линейному тренду добавлен белый шум (разный) 
Линейная регрессия, коэффициент А=0.13 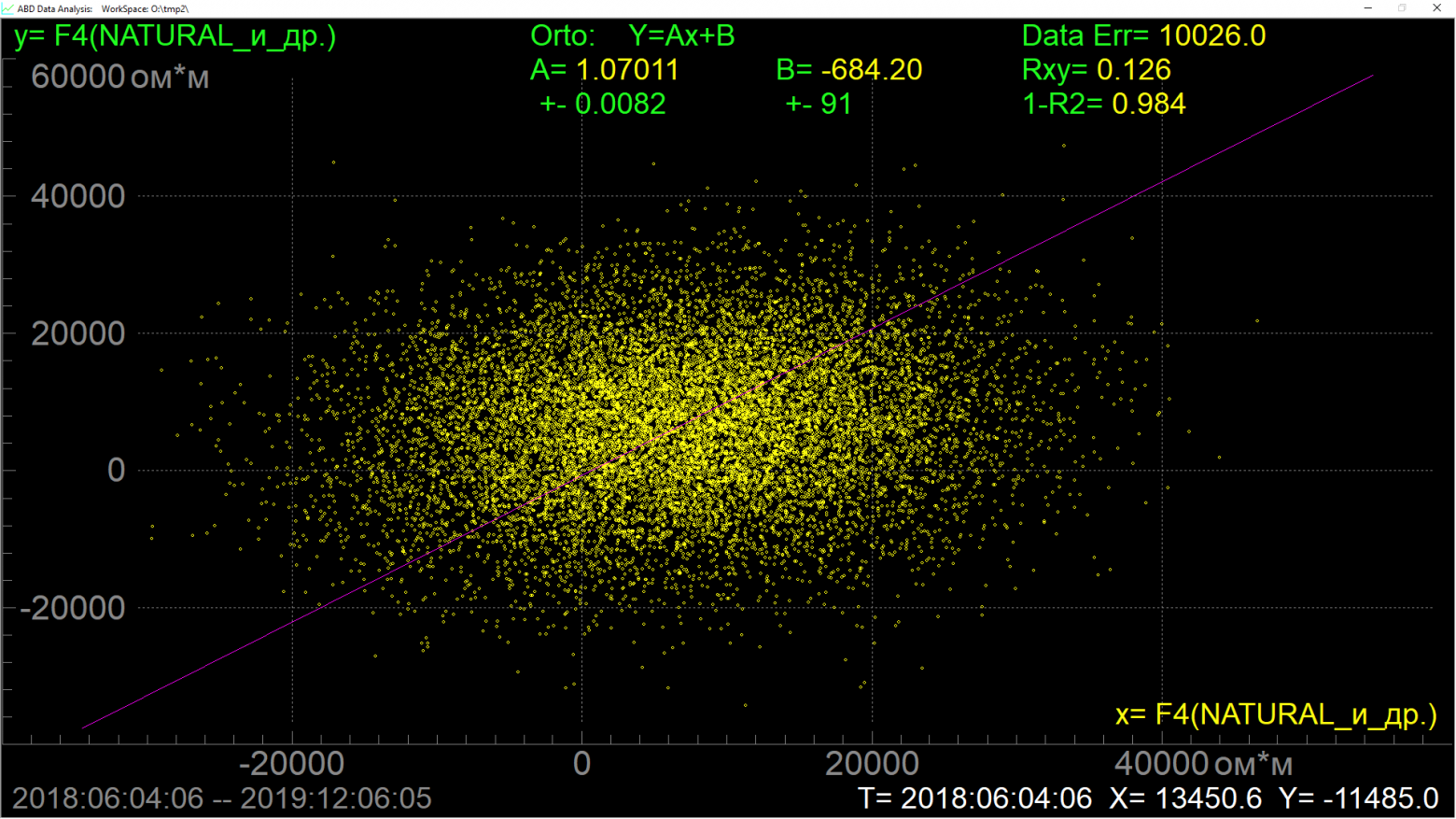
Линейная ортогональная регрессия, коэффициент А=1.07 Фактически на двух последних картинках считается регрессия ряда самого на себя (+шум). Теоретическое значение коэффициента регрессии в обоих случаях, разумеется, единица.
P.S. На шкалы на картинках не обращайте внимания, я для простоты сгенерил синтетические ряды по образцу того, что было в рабочем пространстве. Это просто иллюстрация разницы между двумя способами минимизации невязок.
Но в рамках описанной автором задачи все почему-то упорно используют именно линейную регрессию, как будто независимая переменная известна точно. Хотя вполне очевидно, что при таком дизайне исследования это допущение не выполняется.
Так что не вдаваясь в интерпретации, могу подтвердить, что с матобработкой у авторов оригинальной статьи явно были проблемы.
Что, впрочем, совершенно не удивительно, если познакомиться с приведенным вот тут коротким обзором (смотреть надо в конце стр.71). Сразу несколько разных авторов, анализировавших статьи в медицинских журналах на предмет корректности матобработки, утверждают что в большинстве медицинских исследований статистические методы
применяются неправильно
Данные слегка устаревшие, но тем не менее:
В работе [Hall, 1982] проанализированы публикации одного из известных медицинских журналов Великобритании. Ошибки в применении статистических методов допущены 78% статей:
В работе [Леонов, 2007а] показано, что лишь 10% клинической информации в российских медицинских публикациях подвергается корректному статистическому анализу
В работе [Леонов, Ижевский, 1997] - что t-критерий Стьюдента в половине случаев применяется некорректно (в этой работе тоже рассматривались диссертации и публикации в наиболее известных биомедицинских журналах).
Другие примеры, а также полные библиографические ссылки на упомянутые выше статьи можно найти все в той же нашей работе, которая доступна для скачивания вот здесь. (Если ссылка протухнет, статью также можно найти на ResearchGate)
Да, перечисленные в обзоре работы слегка устарели, и сейчас ситуация
стала немного получше
хотя публикаций с явными ошибками в медицинских журналах по-прежнему полным-полно, но все-таки их не 90%, как раньше, а значительно меньше
Но оригинальная-то работа Д&К (1999) относится-то как раз к тому самому "золотому веку" неведения, про который пишут авторы вышеупомянутого обзора. Когда многие медики еще не вкусили запретный
яблочныйплод от математического древа познания...
NNikolay Автор
01.12.2023 08:29+2Вот такими комментариями и хорош Хабр! Я как-то не подумал ортогональную регрессию привести здесь. Спасибо!

harikein70
01.12.2023 08:29Выводы автора - типичная профанация. Что за поведенческая психология такая? А чем она отличается от когнитивной или экспериментальной или вообще поведенческого анализа?? . Яркий пример поговорки -слышал звон , не зная где он.

NNikolay Автор
01.12.2023 08:29+1Для меня привычнее английский. Я имею ввиду behavioral science. Как желаете перевести? Я думаю из контекста понятно, что я имею ввиду.

Batalmv
01.12.2023 08:29+2Да что же вы эту ветрянную мельницу мучаете то :)
-----------------
Ну смотрите, сначала просто почему это работает. Это ж не про математику, а про психологию. Вот есть Солнце и есть Земля. Все ж видят что Земля большая, Солнце маленькое. Оно движется, его можно закрыть рукой. Значит земля центр мира, а Солнце крутится вокруг и дарит там свет и тепло.
... конечно же нет :), но много веков назад людей которые так думали, было абсолютное большинство. И все эти люди нисколько не сомневались в своем "знании", и более того, окажись вы в то время и вступи с ними в спор - итог скорее всего был бы печальным, но коротким. Т.е. убежденность людей в своей правоте была просто на максимально возможном уровне, а неприятие другой точки зрения макстимально болезненным для его носителя
Но были те, кто знали больше (их сейчас называют экспертами) и они сомневались в этой стройной и всем понятной картине мира. Они исследовали, строили гипотезы и далее последовал ряд открытий. Изменение картины мира, законы Кепплера .. Кто-то нашел целую планету, засомневавшись в том, что результаты измерений известных планет верны. И т.д.
Наука движется сомневающимися людьми, которые способны свои сомнения обратить в тягу к знаниям и методично ищут новую истину.
Таких примеров есть огромное количество и почти всегда "толпе абсолютно уверенных в себе людей" противостоит (слава богу, что не прямо, иначе бы мы все еще были плоскоземельщиками) незначительное число сомневающихся экспертов. Вы только представьте, сколько де......тов, де...ов, ду...ов говорили Колумбу кто он по своим умственным способностям :) И все они свято верили, что правы и знают лучше всех.
Это просто массовый эффект, который вокруг нас все время. Просто мы, к сожалению, не эксперты и часто не даем себе труд сомневаться :)
Но понятно, что просто сомнения тоже не признак ума :)
----------------
Если же вам все таки хочется победить ветряную мельницу ... ну смотрите. Математически опровергать гипотезу как-то не очень продуктивно. Математика сама по себе штука очень в себе. Что рождается в математике, там и остается. Вопрос всегда в том, какие данные вы взяли, и как вы интерпретировали полученный результат. Если есть гипотеза, которая начинается в мире психологии, потом некими числами уходит в математику, и в конце снова в виде интерпретации возвращается в психологию, то чисто формально у вас есть три точки приложения ваших усилий:
найти что не так с входными данными. Наверняка были РЕАЛЬНЫЕ эксперименты и вы можете провести свои собственные, чтобы повторить путь, который уже пройдет и найти ошибку
погрузиться в мир математики, тут (я уже писал вам), можно начать с банального аналитического дополнения к Excel, которвый вам все бесплатно подсчитает. И не надо много писать, скрина будет достаточно тем, кто в теме
попробовать найти ошибку в рассуждениях, которые интерпретируют результаты рассчетов
Попытки же как-то что-то показать на аналогиях и прочем - это просто не имеет смысла в виду лживости аналогий и наличия простого пути, который я описал выше

NNikolay Автор
01.12.2023 08:29Это нормально относиться скептически. Я могу и по Вашей программе тоже:
1) Реальные эксперименты: из недавнего исследование на студентах ВШЭ с похожими выводами - Magnus and Peresetsky 2022.
2) Excel: тут я не очень понял чем Вам не подходит мой код не питоне со скриншотом. Тем что не Excel?
3) Ошибка в рассуждениях: если не нравится мой аргумент с нефальсифицируемостью, то можно почитать более подробно в деталях у Gignac and Zajenkowski 2020. Тоже, кстати, у них сделано своё исследование на 900 респондентах.
Поймите, эта тема разобрана во всех вариантах до очевидности. Стоит только захотеть разобраться.

Batalmv
01.12.2023 08:29Ну блин, там же взята выборка студентов, которым пообещали бонус за точный прогноз :) Но в реальной жизни, к которой и применим эффект, никто бонус не обещает. Никто ж не приходит к вам и говорит - я вам дам бонус, если вы не совещании ... Суть же не в просто проведении неких телодвижений с цифрами. Я ж вам написал "данные" - "модель" - интерпретация. Тут же ж заранее данные взяты в исскуственной среде, которую еще и мотивировали на поведение, отличное от стандартного.
Просто так понятно и точно работает. Или EViews. Сорян, читать код, зачем?
Вы просто осознайте пример с Солнцем и Землей. Вот нагляднейший пример работы эффекта. И он очевиден без математики.
Зачем вы игнорируете реальную жизнь?
=====
Вы поймите. Математикой легко обосновать, что Солнце крутится вокруг Земли. Достаточно просто взять "верные" исходные данные
Вы, и многие, просто идедте сразу в понятную (я так предполагаю) вам область чисел, забывая о том, а что вы вообще считаете
Если вы не делаете корректный переход из реального мира в его модель - дальнейшие "упражнения" не имеют смысла.

NNikolay Автор
01.12.2023 08:29Я не знаю как математикой обосновать, что Солнце крутится вокруг Земли:)

Batalmv
01.12.2023 08:29Да просто, любая задача на движение, векторы с 9-го класса. Точкой отсчета выбирается Земля. И все. В вашей модели, как ни старайся, все крутится относительно ее :)
Например на соударение объектов. Часто для упрощения помещают точку отсчета на один из объектов, корректируя вектор остальных :)

NNikolay Автор
01.12.2023 08:29Видимо вы имеете в виду астрономические наблюдения. Так как раз нельзя обосновать что вокруг чего крутится, так как можно поставить в центр Солнце и мат модель будет тоже соответствовать наблюдениям - оба варианта работают. Заметьте разницу - не "можно обосновать", а именно что "нельзя обосновать". Для вращения Земли строгое доказательство пришло только с маятником Фуко. С эффектом Д-К то же самое - в него можно верить, но нужно понимать, что никаких научных данных нет так как данные прекрасно бьются с моделью вообще без психологии.

NNikolay Автор
01.12.2023 08:29А если по делу - Вы разбирали какая была мотивация в оригинальном исследовании? На самом деле Даннинга с Крюгером критиковали за ОТСУТСВИЕ мотивации по факту. И они даже повторили это исследование с 5$ призами. С тем же результатом. Я, кстати ссылки на два исследования приводил. Вы оба успели посмотреть? Суть как раз в нефальсифицируемости. Хоть с мотивацией, хоть без мотивации, хоть у ВШЭ, хоть в оригинале получается один и тот же результат, который соответствует как модели с шумом так и психологическим объяснениям. Это как с гипотезой о Боге - нефальсифицируема.
Извините, но я на EViews с питона не буду переписывать, так как не верю, что Вы серьёзно это пишите.





Wizard_of_light
Есть много случаев, когда что-то похожее на эффект Данига-Крюгера работает. Водители, например, больше всего попадают в аварии в первый год - когда ещё ничего не умеют, и на третий год - когда думают что уже умеют. (Ну, по статистике ещё и в пятнадцатый - когда у него уже хрен проскочишь :)).
NNikolay Автор
Я так понимаю по описанию, Вы видели вот это исследование - там на графике видны выбросы на 5 и как раз 15 год. Но там очень маленькая выборка только по Латвии и авторы таких выводов по годам тоже не делают. Куча гуглится других статей, где пики на других годах или их вообще не видно (например здесь) - это просто шум похоже.
Wizard_of_light
Нет, вот как раз этого исследования я не видел - я рассматривал статистику ДПС из журнальных публикаций и отчёт региональной ассоциации автошкол Москвы (там правда только до трёхлетнего стажа).