Сравнительный анализ методов аппроксимации на основе SQL-запросов / forpes.ru

Главная
Сравнительный анализ методов аппроксимации на основе SQL-запросов

Сравнительный анализ методов аппроксимации на основе SQL-запросов

11.12.2023 08:31

neoflex 6 2000 Источник

1. Введение

При работе с данными часто приходится сталкиваться с ситуацией, когда имеется некоторая функциональная зависимость y_i = f(x_i), которая получена в результате эксперимента или сбора статистики. То есть исходные данные представлены набором точек (x₁, y₁), (x₂, y₂) … (x_n, y_n), где n – количество экспериментальных значений. Если аналитическое выражение функции f(x) неизвестно или весьма сложно, то возникает чисто практическая задача: найти такую функцию Y = F(x), значения которой при x=x_i будут близки к экспериментальным данным. Приближение функции f(x_i) к более простой F(x) называется аппроксимацией. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. Как правило, выбор модели аппроксимации определяется по минимальному значению погрешности на всем интервале исходных данных. Для расчетов необходимо использовать несколько видов аппроксимаций, чтобы определить более точное описание зависимости экспериментальных данных y = f(x_i). Численным коэффициентом, определяющим надежность аппроксимации принято считать величину R² ("эр-квадрат"). Итак, R²– это величина достоверности аппроксимации, подробней о которой поговорим ниже.

Переход от функциональной зависимости f(x) к аналитической F(x) позволяет нам получить значение F(x) на всей области определения, а если x временная переменная, то в каком-то смысле и заглянуть в будущее. Другими словами, если известна F(x), то подставляя в нее произвольные x, можно получить значения функции в тех точках, где f(x) была не определена. Действительно, если есть аналитическая функция, то можно попытаться подставить в нее произвольное значение, а не только те значения, которые были в эксперименте. Такой способ позволяет нам спрогнозировать дальнейшее развитие событий, что безусловно является сильной стороной аппроксимации.

Все числа, получаемые при измерениях, являются приближенными. Увы, никакое измерение нельзя выполнить абсолютно точно. Причин тому достаточное количество: это и ограниченные возможности измерительного оборудования, и несовершенство органов чувств, и неоднородность измерительных объектов, а также внешние и внутренние факторы, влияющие на объекты. Систематические и приборные ошибки связаны с конструктивными особенностями приборов измерения и неточностями методов измерений. Работая с уже имеющимся экспериментальным результатом, мы не можем повлиять на данный вид ошибок. Другое дело, если речь идет об ошибках случайных. Действительно, при малом объеме данных вполне может оказаться, что результаты эксперимента оцениваются исходя из случайного преобладания маловероятных исходов. В этом случае существует значительная вероятность большой ошибки. Следует помнить, что увеличение числа измерений уменьшает влияние случайных ошибок. Другими словами, чтобы повысить достоверность данных, нам потребуется работать с большим количеством экспериментов. А для работы с большими числовыми массивами лучше всего подходят те базы данных, которые легко масштабируются. Таким образом, речь прежде всего пойдет об обработке данных на основе запросов к таким базам как GreenPlum/Postgres и Hive. Вместе с тем, предложенный подход легко может быть перенесен и на другие базы данных.

К настоящему времени существует множество библиотек и программных продуктов, в которых реализованы те или иные методы аппроксимации. Не будем останавливаться здесь подробно, скажем лишь, что такие возможности присутствуют как в известных математических пакетах, так и программных продуктах, нацеленных на решение такого рода задач. Проблема здесь в том, что исходные экспериментальные данные, особенно если речь идет о больших числовых массивах, как правило хранятся в специально предназначенных для этого базах данных. Процесс передачи данных во внешние приложения может оказаться достаточно трудоемкой задачей, а порой так и вовсе неразрешимой. В данной статье мы хотим показать, что для решения задач аппроксимации совсем не обязательно использовать сторонние инструменты. Если ваши экспериментальные данные хранятся в базе, и есть возможность выполнять к данным SQL запросы, значит у нас есть все необходимое, чтобы решить задачу аппроксимации.

2. Аппроксимация: метод наименьших квадратов

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от экспериментальных входных данных. Минимальность отличий между исходной f(x) и аппроксимирующей функции F(x) определяется числовой мерой, а именно: сумма квадратов отклонений f(x) от F(x) должна быть наименьшей [1].

Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений расчетной аппроксимирующей функции от заданного массива экспериментальных данных. Данный критерий метода наименьших квадратов записывается в виде следующего выражения:

$\sum_{i=1}^{N}{\left[y_i-F\left(x_i\right)\right]^2 \to min}.\mspace{72mu} (1)$

Здесь F(x_i) – значения расчетной аппроксимирующей функции в узловых точках, x_i, y_i – заданный массив экспериментальных данных в узловых точках x_i.

Использование метода наименьших квадратов позволяет:

ответить на вопрос: есть ли зависимость между x_i и y_i;
получить оптимальную аналитическую модель;
рассчитать параметры регрессионного уравнения, характеризующего аналитическую модель.

Ответ на первые два вопроса может дать расчет так называемой величины достоверности R², которая в свою очередь может быть оценена на основе выбранной аналитической модели F(x). Величина достоверности (она же – коэффициент детерминации) согласно [2] может быть рассчитана следующим образом:

$R^2=1-\frac{\sum_{i=1}^{N}\left[y_i-F(x_i)\right]^2}{\sum_{i=1}^{N}\left[y_i-\bar{F}(x_i)\right]^2},\mspace{72mu}(2)$

где:

$\sum_{i=1}^{N}\left[y_i-F\left(x_i\right)\right]^2$

– сумма квадратов остатков регрессии; y_iи F(x_i)– фактическое и расчетное значение переменной y в данной точке x,

$\sum_{i=1}^{N}\left[y_i-\bar{F}\left(x_i\right)\right]^2$

– сумма квадратов разности между фактическим и средним значением F(x_i), N – число точек. [2].

Чем ближе значение коэффициента R²к 1, тем лучше полученный результат. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50 %. Модели с коэффициентом детерминации выше 80 % можно признать достаточно хорошими.

Конкретный вид аппроксимирующей функции выбирается, как правило, из физических соображений. А значит, это могут быть линейная, экспоненциальная, степенная, полиномиальная, обратная и другие функции.

Будем считать, что вид аппроксимирующей зависимости выбран и ее можно записать в виде:

$y=F(x,\text{a}_0,\text{a}_1,...,\text{a}_m),\ \ \ \ \ \ m\le\ N-1,\mspace{72mu}(3)$

где F – известная функция, a₀, a₁, … a_m– неизвестные постоянные параметры, значения которых надо найти. В методе наименьших квадратов приближение функции (3) к экспериментальной зависимости считается наилучшим, если выполняется условие:

$Q=Q\left(\text{a}_0,\text{a}_1,\ldots,\text{a}_m\right)=\sum_{i=1}^{N}\left(y_i-F\left(x_i,\text{a}_0,\text{a}_1,\ldots,\text{a}_m\right)\right)^2 \to min.\mspace{72mu}(4)$

То есть суммa квадратов отклонений искомой аналитической функции от экспериментальной зависимости должна быть минимальна.

Необходимым условием минимума функции нескольких переменных является равенство нулю всех частных производных этой функции по параметрам. Таким образом, отыскание наилучших значений параметров аппроксимирующей функции (3), то есть таких их значений, при которых

$Q=Q\left(\text{a}_0,\text{a}_1,\ldots,\text{a}_m\right)$

минимальна, сводится к решению системы уравнений:

$\left\{\begin{matrix} \large\frac{\partial Q}{\partial \text{a}_0}=0\\\begin{matrix}\large\frac{\partial Q}{\partial \text{a}_1}=0\\...\\\large\frac{\partial Q}{\partial \text{a}_m}=0\\\end{matrix}\\\end{matrix}\right. \mspace{72mu}(5)$

Строго говоря, с точки зрения математики, такое условие не является достаточным. Для того, чтобы быть уверенным в том, что перед нами действительно минимум функции, а не просто экстремум, надо еще дополнительно убедиться, что вторые производные функции Q по параметрам a_i больше нуля. Для простоты мы не будем выполнять такие расчеты, а будем исходить из того, что в случае, если построенная аппроксимация плохо описывает эксперимент (R²< 0,5), то будем считать такую аппроксимацию неудовлетворительной.

3. Практика: пример аппроксимации на основе Excel

Одним из самых простых инструментов, с помощью которых можно построить аппроксимацию на основе экспериментальных данных, можно считать Excel из пакета Microsoft Office. Давайте посмотрим на то, как работает простейший вид аппроксимации на реальном примере. Excel позволяет нам не только построить аналитическую зависимость F(x), он еще и позволяет увидеть все численные коэффициенты как самой аналитической зависимости, так и величину достоверности.

В качестве экспериментального результата для исследования возьмем статистику роста интернет пользователей в зависимости от года (см. рис. 1) [3].

Рис.1Ежегодная статистика количества интернет пользователей [3]. — Рис.1
Ежегодная статистика количества интернет пользователей [3].

Перенесем имеющиеся у нас экспериментальные результаты в Excel и построим аппроксимацию (линию тренда). В качестве таковой выберем простейший вариант – линейной зависимости (Linear). Также в свойствах аппроксимации отметим галочками такие как «Display Equation on chart» (отобразить формулу в явном виде) и «Display R-squared value on chat» (показать величину R²). И то, и другое можно видеть на рисунке. Добавим к построению теоретической зависимости диапазон для будущих годов – Forecast forward (в нашем случае установлен в 5, что значит продлить зависимость еще на 5 лет). То есть мы с определённой степенью точности можем предсказать, как будут развиваться события в будущем (пунктирная часть красной линии: та, что больше 2022 года). Можно сказать, что полученная аппроксимация [F(x) = 0,242x – 0,5291] (см. рис. 2) весьма хорошо описала эксперимент. Такой вывод можно сделать не только из визуального совпадения. Важнее, что величина R² оказалась существенно выше, чем требуется в теории (более 80% – хорошее совпадение), но можно ли считать, что такая аналитическая кривая наилучшим образом описывает эксперимент? В принципе можно, но лишь до того момента, пока не будет найдена иная аналитическая кривая, у которой величина достоверности больше той, что мы видим на рисунке. Таким образом, в теории, мы получили ответы на поставленные вопросы – большая величина коэффициента R² говорит о том, что есть зависимость между аргументами и полученными значениями, мы также получили численные значения для аналитической зависимости (коэффициенты a и b), и, хотя у нас на данный момент нет ответа, является ли данная аппроксимация наилучшей, можно считать, что она хорошо описывает имеющийся экспериментальный материал (см. рис. 2).

Рис. 2. Линия тренда (аппроксимация) на основе экспериментальных данных с учетом прогноза на последующие несколько лет. Для простоты расчета будем отсчитывать время наблюдения от 2005 года, т.е. 2005 год – это первый год наблюдения — Рис. 2.
Линия тренда (аппроксимация) на основе экспериментальных данных с учетом прогноза на последующие несколько лет. Для простоты расчета будем отсчитывать время наблюдения от 2005 года, т.е. 2005 год – это первый год наблюдения

4. Практика: аппроксимация простейшими функциями

Теперь выполним самостоятельно ряд расчетов на основе теории, изложенной выше. В качестве функций для аппроксимации выберем ряд простейших функций. Очевидно, что для описания имеющегося экспериментального результата необходимо использовать возрастающую функцию. Таким образом, нам подойдут не все функции, однако не будем исключать на данном этапе иные варианты, поскольку их вполне можно использовать для описания других экспериментальных результатов.

4.1 Линейная функция

Рассмотрим, как это работает на простом примере линейной функции. Будем считать, что F(x_i) = ax_i + b. Тогда перепишем формулу (1) следующим образом:

$\sum_{i=1}^{N}{\left({\text{a}x}_i+b-y_i\right)^2\rightarrow min}\mspace{72mu}(6)$

Переменными в данном случае выступают a и b, а поскольку результат должен стремиться к нулю, то можно записать условие экстремума по переменным a и b (см. (5)):

$\left\{\begin{matrix}\frac{\partial}{\partial \text{a}}\sum_{i=1}^{N}{\left(\text{a}x_i+b-y_i\right)^2=0}\\\frac{\partial}{\partial b}\sum_{i=1}^{N}{\left(\text{a}x_i+b-y_i\right)^2=0}\\\end{matrix}\right.$

Отсюда несложно получить:

$\left\{\begin{matrix}\text{a}\sum_{i=1}^{N}{x_i^2+b\sum_{i=1}^{N}{x_i=}}\sum_{i=1}^{N}{x_iy_i}\\\text{a}\sum_{i=1}^{N}{x_i+bN=}\sum_{i=1}^{N}y_i\\\end{matrix}\right.$

Выразив a и b, получим следующий результат:

$\left\{\begin{matrix}\text{a}=\Large\frac{N\sum_{i=1}^{N}{\left(x_iy_i\right)-\sum_{i=1}^{N}{x_i\sum_{i=1}^{N}y_i}}}{N\sum_{i=1}^{N}x_i^2-\left(\sum_{i=1}^{N}x_i\right)^2}\\b=\Large\frac{\sum_{i=1}^{N}{x_i^2\sum_{i=1}^{N}y_i-\sum_{i=1}^{N}{x_i\sum_{i=1}^{N}\left(x_iy_i\right)}}}{N\sum_{i=1}^{N}x_i^2-\left(\sum_{i=1}^{N}x_i\right)^2}\\\end{matrix}\right..\mspace{72mu}(7)$

Теперь коэффициенты a и b можно подставить в уравнение F(x) = ax + b в явном виде.

Создадим таблицу для работы с экспериментальными данными. В простейшем виде это будет таблица tbl_iu с двумя полями yiu INTEGER, ciu FLOAT. Наполним ее теме же данными, что присутствуют на рис. 1 и 2. Год будем отчитывать от единицы: поле yiu (YearInternetUsers), а поле ciu (CountInternetUsers) будет отвечать за количество пользователей. Теперь ничто не мешает нам записать соответствующее view для построения линейной зависимости (см. листинг 1). Тут замечу, что листинг 1 включает дополнительные расчеты для других типов аппроксимаций, необходимость в которых будет объяснена позже. Для оценки величины достоверности R² нам потребуется еще один запрос, основанный на формуле 2. Поскольку у нас есть все необходимые параметры, его также можно написать в явном виде. Такой запрос можно увидеть на листинге 2.

CREATE OR REPLACE VIEW approximation AS
WITH
  k_yval AS (SELECT MAX(yiu)                 AS max_year
                  , MIN(yiu) - 1             AS min_year
               FROM tbl_iu)
, k_stat AS (SELECT yiu::decimal - min_year  AS xi
                  , ciu                      AS yi
               FROM tbl_iu 
                  , k_yval)
, k_par AS (SELECT COUNT(1)                  AS cnt
                 , SUM(xi * xi)              AS sum_xx
                 , SUM(xi * yi)              AS sum_xy
                 , SUM(yi * yi)              AS sum_yy
                 , SUM(LN(xi))               AS sum_ln_x
                 , SUM(LN(yi))               AS sum_ln_y
                 , SUM(xi * LN(yi))          AS sum_x_ln_y
                 , SUM(yi * LN(xi))          AS sum_y_ln_x
                 , SUM(LN(xi) * LN(xi))      AS sum_ln_x_ln_x
                 , SUM(LN(xi) * LN(yi))      AS sum_ln_x_ln_y
                 , SUM(1 / yi)               AS sum_dy
                 , SUM(1 / xi)               AS sum_dx
                 , SUM(xi / yi)              AS sum_xdy
                 , SUM(yi / xi)              AS sum_ydx
                 , SUM((1 / xi) * (1 / xi))  AS sum_dxdx
                 , SUM(xi)                   AS sum_x
                 , SUM(yi)                   AS sum_y
              FROM k_stat)
, k_app AS (SELECT (cnt * sum_xy - sum_x * sum_y) 
                 / (cnt * sum_xx - sum_x * sum_x)                          AS a_lin
                 , (sum_xx * sum_y - sum_x * sum_xy) 
                 / (cnt * sum_xx - sum_x * sum_x)                          AS b_lin
                 , EXP(
                     (sum_ln_y * sum_xx - sum_x * sum_x_ln_y) 
                   / (cnt * sum_xx - sum_x * sum_x)
                   )                                                       AS a_exp
                 , (cnt * sum_x_ln_y - sum_x * sum_ln_y) 
                 / (cnt * sum_xx - sum_x * sum_x)                          AS b_exp
                 , EXP(
                     (sum_ln_y * sum_ln_x_ln_x - sum_ln_x * sum_ln_x_ln_y) 
                   / (cnt * sum_ln_x_ln_x - sum_ln_x * sum_ln_x)
                   )                                                       AS a_pwr
                 , (cnt * sum_ln_x_ln_y - sum_ln_x * sum_ln_y) 
                 / (cnt * sum_ln_x_ln_x - sum_ln_x * sum_ln_x)             AS b_pwr
                 , (sum_ln_x_ln_x * sum_y - sum_ln_x * sum_y_ln_x) 
                 / (cnt * sum_ln_x_ln_x - sum_ln_x * sum_ln_x)             AS a_log
                 , (cnt * sum_y_ln_x - sum_ln_x * sum_y) 
                 / (cnt * sum_ln_x_ln_x - sum_ln_x * sum_ln_x)             AS b_log
                 , (sum_xx * sum_dy - sum_x * sum_xdy) 
                 / (cnt * sum_xx - sum_x * sum_x)                          AS a_inv
                 , (cnt * sum_xdy - sum_x * sum_dy) 
                 / (cnt * sum_xx - sum_x * sum_x)                          AS b_inv
                 , (sum_dxdx * sum_y - sum_dx * sum_ydx)
                 / (cnt * sum_dxdx - sum_dx * sum_dx)                      AS a_hyp
                 , (cnt * sum_ydx - sum_dx * sum_y)
                 / (cnt * sum_dxdx - sum_dx * sum_dx)                      AS b_hyp
              FROM k_par)
SELECT x                                     AS x_year
     , y_real                                AS y_users
     , k_app.a_lin                           AS a_lin
     , k_app.b_lin                           AS b_lin
     , x * k_app.a_lin + k_app.b_lin         AS y_approximation
  FROM (SELECT CASE 
                 WHEN x_year < 0 THEN max_year - x_year - k_yval.min_year 
                 ELSE x_year - k_yval.min_year 
               END AS x
             , y_real
             , CASE WHEN x_year < 0 THEN max_year - x_year ELSE x_year END AS x_year
          FROM (SELECT yiu AS x_year
                     , ciu AS y_real
                  FROM tbl_iu
                 UNION ALL
                SELECT -1 * ROW_NUMBER() OVER (ORDER BY yiu) AS x_year
                     , NULL AS y_real
                  FROM (SELECT UNNEST(STRING_TO_ARRAY(LPAD('', 5-1, ','), ',')) AS yiu) AS t0
               ) t1
             , k_yval
         ORDER BY x_year
       ) t_in
 CROSS JOIN k_app
 ORDER BY x_year

--                            Листинг 1.  
-- Набор точек, соответствующих линейной аппроксимации.

WITH app_avg
  AS (SELECT AVG(y_approximation)         AS y_app_avg
        FROM approximation app_in
       WHERE y_users IS NOT NULL
     )
 SELECT 1
      - SUM(POWER(y_users - y_approximation, 2))
       / SUM(POWER(y_users - y_app_avg, 2)) AS R2
   FROM (SELECT x_year
              , y_users
              , y_approximation
           FROM approximation
          WHERE y_users IS NOT NULL
        ) t0
      , app_avg

--                           Листинг 2. 
-- Расчет величины достоверности R2 для варианта линейной аппроксимации

Полученные таким образом результаты представлены на рис. 3

Рис. 3 Линейная аппроксимация y = ax + b, построенная на основе Листинга 1. — Рис. 3
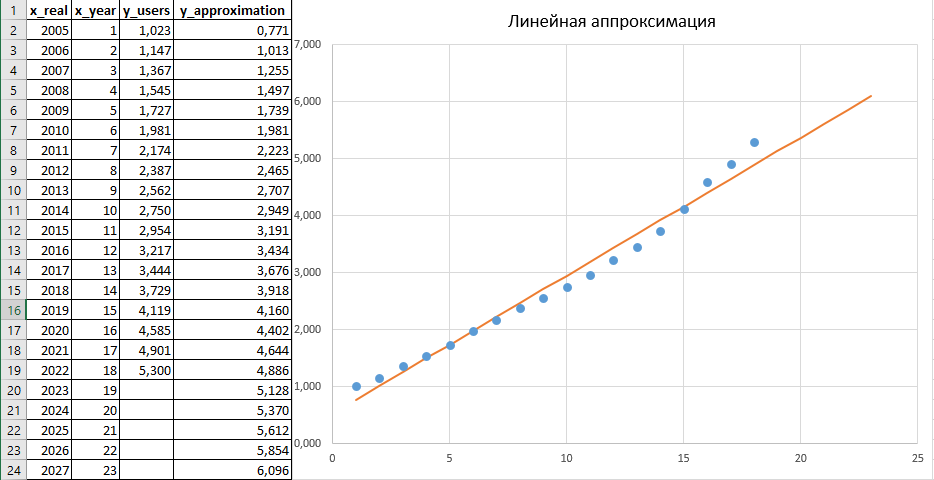
Линейная аппроксимация y = ax + b, построенная на основе Листинга 1.

В расчете (Листинги 1, 2) были получены следующие численные значения: a_lin = 0,242; b_lin = 0,5291; R²= 0,9782, что говорит о хорошем совпадении аппроксимации с эмпирическими данными.

4.2 Экспоненциальная функция

$y=\text{a}\cdot exp(bx)\mspace{72mu}(8)$

Снова решаем систему уравнений (5), но уже для другого вида функций аппроксимации (8). Проще всего это сделать, выполнив замену вида:

$X=x;\ \ Y=ln(y);\ \ A=b;\ \ B=ln(\text{a})\ \mspace{72mu}(9)$

отсюда (8) можно записать как Y = B + AX, таким образом решение сводится к уже проделанному ранее (см. формулу 7):

$\left\{\begin{matrix}A=\large\frac{N\sum_{i=1}^{N}{\left(X_iY_i\right)-\sum_{i=1}^{N}{X_i\sum_{i=1}^{N}Y_i}}}{N\sum_{i=1}^{N}X_i^2-\left(\sum_{i=1}^{N}X_i\right)^2}\\B=\large\frac{\sum_{i=1}^{N}{X_i^2\sum_{i=1}^{N}Y_i-\sum_{i=1}^{N}{X_i\sum_{i=1}^{N}\left(X_iY_i\right)}}}{N\sum_{i=1}^{N}X_i^2-\left(\sum_{i=1}^{N}X_i\right)^2}\\\end{matrix}\right.\mspace{72mu}(10)$

Выполнив обратную замену в соответствии с (9), получим:

$\left\{\begin{matrix}\text{a}=exp\left\{\Large\frac{\sum_{i=1}^{N}{ln\left(y_i\right)\sum_{i=1}^{N}x_i^2-\sum_{i=1}^{N}{x_i\sum_{i=1}^{N}\left[x_iln\left(y_i\right)\right]}}}{N\sum_{i=1}^{N}x_i^2-\left(\sum_{i=1}^{N}x_i\right)^2}\right\}\\b=\Large\frac{N\sum_{i=1}^{N}\left[x_iln\left(y_i\right)\right]-\sum_{i=1}^{N}{x_i\sum_{i=1}^{N}ln\left(y_i\right)}}{N\sum_{i=1}^{N}x_i^2-\left(\sum_{i=1}^{N}x_i\right)^2}\\\end{matrix}\right.\mspace{72mu}(11)$

Теперь коэффициенты a и b можно подставить в уравнение (8) в явном виде. Аналогично предыдущему расчету можем записать соответствующий SQL запрос для построения экспоненциальной зависимости. Не будем, по сути, дублировать листинг 1, запишем только ту часть листинга, которую придётся скорректировать при переходе к экспоненциальной функции.

….
SELECT x                                     AS x_year
     , y_real                                AS y_users
     , k_app.a_exp                           AS a_exp
     , k_app.b_exp                           AS b_exp
     , k_app.a_exp * EXP(k_app.b_exp * x)    AS y_approximation
….
--                             Листинг 3. 
-- Изменения в листинге 1, соответствующие экспоненциальной аппроксимации (строки 57-61)

Полученные таким образом результаты представлены на рис. 4:

Рис. 4Экспоненциальная аппроксимация y = a∙exp(bx), построенная на основе Листинга 3. — Рис. 4
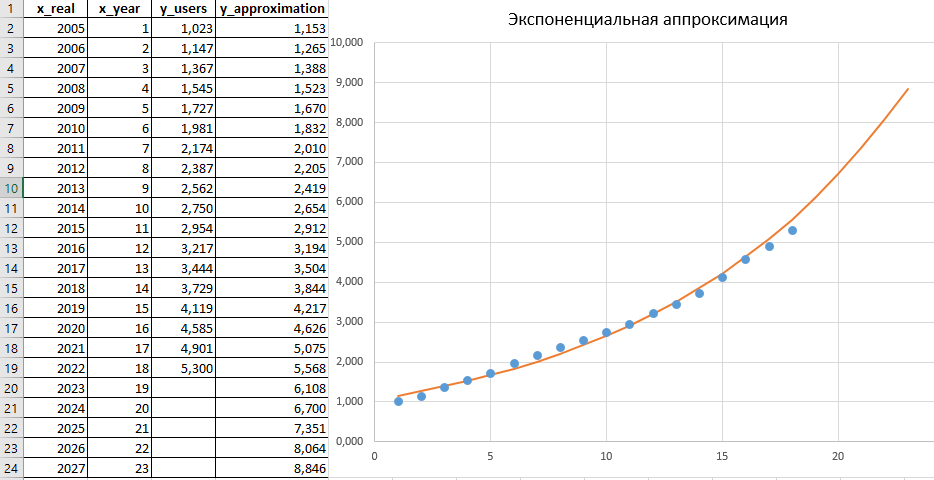
Экспоненциальная аппроксимация *y = a∙exp(bx),* построенная на основе Листинга 3.

В расчете (Листинги 3 и 2) были получены следующие численные значения a_exp = 1,051; b_exp = 0,0926; R²= 0,9903, что говорит о хорошем совпадении аппроксимации с эмпирическими данными.

Следует отметить, что в общем виде формула 8 могла бы содержать дополнительное слагаемое – c, т. е. могла бы быть записана следующим образом: y=a∙exp(bx)+c. К сожалению, в таком виде свести функцию к линейному виду, а следовательно, решить
аналитически уравнение методом МНК – не получится. Однако, если наблюдаемая
экспериментальная зависимость, как и в нашем случае, возрастает (b > 0), а
асимптотой является горизонтальная прямая, не совпадающая с осью Х, то величина
с может быть определена как смещение по оси Y, т.е. c – расстояние от оси X до
асимптоты. Тогда задачу можно будет решить в новой системе координат, где y_new= y – c, после чего вернуться к «старой» системе.

4.3 Степенная функция

$y=\text{a}\cdot x^b.\mspace{72mu}(12)$

Аналогично предыдущему пункту выполним линеаризацию ln(y) = ln(a) + b∙ln(x), отсюда переобозначение:

$X=ln(x); Y=ln(y); A=b; B=ln(\text{a}).\mspace{72mu}(13)$

Получим такое же решение, как и в (10), а выполнив обратные преобразования (13), получаем:

$\left\{\begin{matrix}\text{a}=exp\left\{\Large\frac{\sum_{i=1}^{N}{ln\left(y_i\right)\sum_{i=1}^{N}\left[ln\left(x_i\right)\right]^2-\sum_{i=1}^{N}{ln\left(x_i\right)\sum_{i=1}^{N}\left[ln\left(x_i\right)ln\left(y_i\right)\right]}}}{N\sum_{i=1}^{N}\left[ln\left(x_i\right)\right]^2-\left[\sum_{i=1}^{N}ln\left(x_i\right)\right]^2}\right\}\\b=\Large\frac{N\sum_{i=1}^{N}\left[ln\left(x_i\right)ln\left(y_i\right)\right]-\sum_{i=1}^{N}ln\left(x_i\right)\sum_{i=1}^{N}ln\left(y_i\right)}{N\sum_{i=1}^{N}\left[ln\left(x_i\right)\right]^2-\left[\sum_{i=1}^{N}ln\left(x_i\right)\right]^2}\\\end{matrix}\right.\mspace{72mu}(14)$

Теперь коэффициенты a и b можно подставить в уравнение (12) в явном виде. Аналогично предыдущему расчету можем записать соответствующий SQL-запрос для построения степенной зависимости. По сути не будем дублировать листинг 1, а запишем только ту его часть, которую придётся скорректировать при переходе к степенной функции.

….
SELECT x                                     AS x_year
     , y_real                                AS y_users
     , k_app.a_pwr                           AS a_pwr
     , k_app.b_pwr                           AS b_pwr
     , k_app.a_pwr * POWER(x, k_app.b_pwr)   AS y_approximation 
….

--                             Листинг 4. 
-- Изменения в листинге 1, соответствующие степенной аппроксимации (строки 57-61)

Полученные таким образом результаты представлены на рис. 5:

Рис. 5Степенная аппроксимация y = a ∙ x b, построенная на основе листинга 4. — Рис. 5
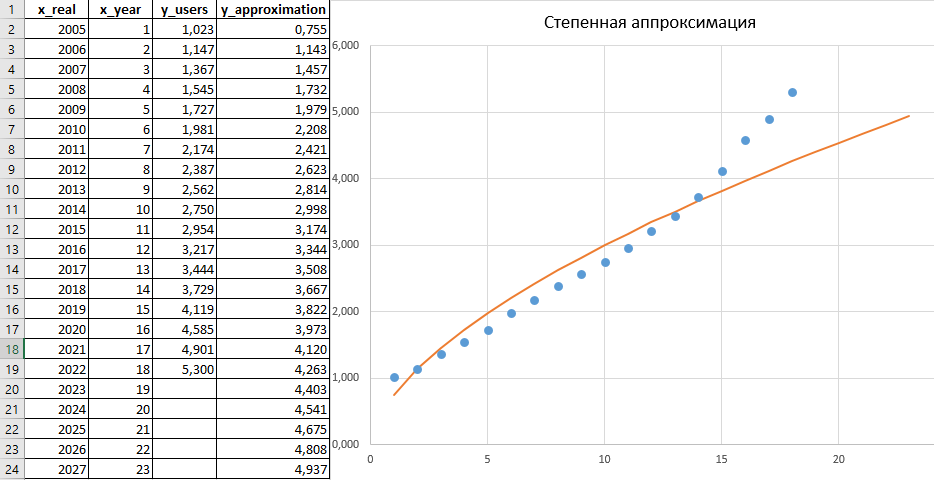
Степенная аппроксимация *y = a ∙ x ^b*_, построенная на основе листинга 4.

В расчете (Листинги 4 и 2) были получены следующие численные значения: a_pwr = 0,7548; b_pwr = 0,599; R² = 0,9073. Здесь согласие с эмпирическими данными неплохое, однако не лучшее.

Аналогично, как и в параграфе 4.3 формула 12, в общем виде могла бы содержать дополнительное слагаемое – с. То есть могла бы быть записана следующим образом: y = a∙x^b + c. Здесь мы получаем аналогичную ситуацию, когда решение может быть найдено только переопределением системы координат. Т.е. выполнив смещение по оси Y на с, мы можем попытаться получить более точную аппроксимацию, в данном случае с = y(0).

4.4 Логарифмическая функция

$y=\text{a}+b\cdot ln(x).\mspace{72mu}(15)$

Линеаризация Y = B+AX и переобозначение:

$X=ln(x); Y=y; A=b; B=\text{a}.\mspace{72mu}(16)$

Отсюда получим такое же решение, как и в (10), а выполнив обратные преобразования (16), получаем:

$\left\{\begin{matrix}\text{a}=\Large\frac{N\sum_{i=1}^{N}\left[y_iln\left(x_i\right)\right]-\ \sum_{i=1}^{N}{ln\left(x_i\right)\sum_{i=1}^{N}y_i}\ \ \ \ }{N\sum_{i=1}^{N}\left[ln\left(x_i\right)\right]^2-\left[\sum_{i=1}^{N}ln\left(x_i\right)\right]^2}\\b=\Large\frac{\sum_{i=1}^{N}\left[ln\left(x_i\right)\right]^2\sum_{i=1}^{N}{y_i-\sum_{i=1}^{N}{ln\left(x_i\right)\sum_{i=1}^{N}\left[y_iln\left(x_i\right)\right]}}}{N\sum_{i=1}^{N}\left[ln\left(x_i\right)\right]^2-\left[\sum_{i=1}^{N}ln\left(x_i\right)\right]^2}\\\end{matrix}\right.\mspace{72mu}(17)$

Теперь коэффициенты a и b можно подставить в уравнение (15) в явном виде. Аналогично предыдущему расчету можем записать соответствующий SQL-запрос для построения логарифмической зависимости. По сути не будем дублировать листинг 1, запишем только ту его часть, которую придётся скорректировать при переходе к логарифмической функции.

….
SELECT x                                     AS x_year
     , y_real                                AS y_users
     , k_app.a_log                           AS a_log
     , k_app.b_log                           AS b_log
     , k_app.a_log + k_app.b_log * LN(x)     AS y_approximation
….

--                             Листинг 5. 
-- Изменения в листинге 1, соответствующие логарифмической аппроксимации (строки 57-61)

Полученные таким образом результаты представлены на рис. 6:

Рис. 6Логарифмическая аппроксимация y = a + b ∙ ln(x), построенная на основе листинга 5. — Рис. 6
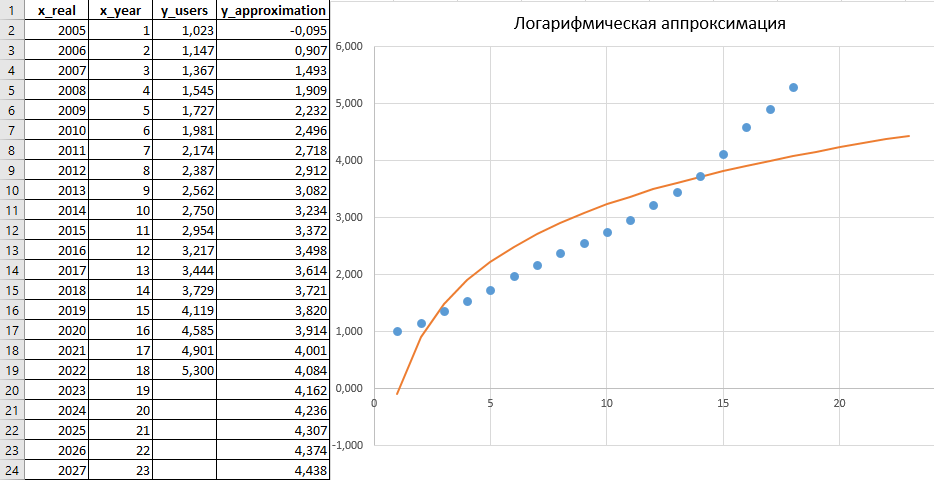
Логарифмическая аппроксимация *y = a + b ∙ ln(x)*, построенная на основе листинга 5.

В расчете (листинги 5 и 2) были получены следующие численные значения a_log = -0,0951; b_log = 1,4459; R²= 0,7876. Здесь величину достоверности уже нельзя считать удовлетворительной.

4.5 Обратная функция

$y=\frac{1}{\text{a}+b\cdot x}\mspace{72mu}(18)$

По виду функции можно сразу сделать вывод, что она не сможет корректно описать рассматриваемый пример. Но не будем сводить все к нашему частному случаю, так как такая функция в теории может прекрасно подойти для описания другой экспериментальной зависимости. А значит есть смысл рассмотреть ее более подробно.

Линеаризация Y = B+AX и переобозначение:

$X=x; Y=1/y; A=b; B=\text{a}.\mspace{72mu}(19)$

Отсюда получим такое же решение, как и в (10), а выполнив обратные преобразования (19) получаем:

$\left\{\begin{matrix}\text{a}=\Large\frac{\ \sum_{i=1}^{N}{x_i^2\sum_{i=1}^{N}{\frac{1}{y_i}-\sum_{i=1}^{N}{x_i\sum_{i=1}^{N}\left(\frac{x_i}{y_i}\right)}}}\ \ \ }{N\sum_{i=1}^{N}x_i^2-\left(\sum_{i=1}^{N}x_i\right)^2}\\b=\Large\frac{N\sum_{i=1}^{N}\left(\frac{x_i}{y_i}\right)-\ \sum_{i=1}^{N}{x_i\sum_{i=1}^{N}\frac{1}{y_i}}}{N\sum_{i=1}^{N}x_i^2-\left(\sum_{i=1}^{N}x_i\right)^2}\\\end{matrix}\right. \mspace{72mu}(20)$

Теперь коэффициенты a и b можно подставить в уравнение (18) в явном виде. Аналогично предыдущему расчету можем записать соответствующий SQL-запрос для построения обратной зависимости. Запишем только ту часть листинга 1, которую придется скорректировать при переходе к обратной функции.

….
SELECT x                                     AS x_year
     , y_real                                AS y_users
     , k_app.a_inv                           AS a_inv
     , k_app.b_inv                           AS b_inv
     , 1 / (k_app.a_inv + k_app.b_inv * x)   AS y_approximation
….

--                             Листинг 6. 
-- Изменения в листинге 1, соответствующие обратной аппроксимации (строки 57-61)

Полученные таким образом результаты представлены на рис. 7:

Рис. 7Обратная аппроксимация y = 1 / (a + b∙x) построенная на основе листинга 6. — Рис. 7
Обратная аппроксимация y = 1 / (a + b∙x) построенная на основе листинга 6.

В расчете (листинги 6 и 2) были получены следующие численные значения: a_inv = 0,8356; b_inv = -0,0411; R²= -0,1197. Здесь величину достоверности уже нельзя считать удовлетворительной. Нетрудно заметить, что функция (18) проходит через точку разрыва второго рода, то есть в точке x = -a/b не существует. Мы не увидели этого разрыва на графике в силу низкой точности аппроксимации. Это как раз тот случай, когда однозначно понятно, что обратная функция точно не подходит для построения линии тренда имеющегося экспериментального материала.

4.6 Гиперболическая функция

$y=\text{a}+\frac{b}{x}.\mspace{72mu}(21)$

Линеаризация Y = B+AX и переобозначение:

$X=1/x; Y=y; A=b; B=\text{a}.\mspace{72mu}(22)$

Отсюда получим такое же решение, как и в (10), а выполнив обратные преобразования (22) получаем:

$\left\{\begin{matrix}\text{a}=\Large\frac{\ \sum_{i=1}^{N}{\left(\large\frac{1}{x_i}\right)^2\sum_{i=1}^{N}{y_i-\sum_{i=1}^{N}{\frac{1}{x_i}\sum_{i=1}^{N}\left(\frac{y_i}{x_i}\right)}}}\ \ \ }{N\sum_{i=1}^{N}\left(\frac{1}{x_i}\right)^2-\left(\sum_{i=1}^{N}\frac{1}{x_i}\right)^2}\\b=\Large\frac{N\sum_{i=1}^{N}\left(\frac{y_i}{x_i}\right)-\ \sum_{i=1}^{N}{\frac{1}{x_i}\sum_{i=1}^{N}y_i}}{N\sum_{i=1}^{N}\left(\frac{1}{x_i}\right)^2-\left(\sum_{i=1}^{N}\frac{1}{x_i}\right)^2}\\\end{matrix}\right..\mspace{72mu}(23)$

Теперь коэффициенты a и b можно подставить в уравнение (21) в явном виде. Аналогично предыдущему расчету можем записать соответствующий SQL-запрос для построения гиперболической зависимости. Запишем только ту часть листинга 1, которую придётся скорректировать при переходе к гиперболической функции.

….
SELECT x                                     AS x_year
     , y_real                                AS y_users
     , k_app.a_hyp                           AS a_hyp
     , k_app.b_hyp                           AS b_hyp
     , k_app.a_hyp + k_app.b_hyp / x         AS y_approximation
….

--                             Листинг 7. 
-- Изменения в листинге 1, соответствующие гиперболической аппроксимации (строки 57-61)

Результаты, полученные таким образом, представлены на рис. 8:

Рис. 8Гиперболическая аппроксимация y = a + b/x построенная на основе листинга 7. — Рис. 8
Гиперболическая аппроксимация *y = a + b/x* построенная на основе листинга 7.

В расчете (Листинги 7 и 2) были получены следующие численные значения: a_hyp = 3,5503; b_hyp = -3,7176; R²= 0,4345, здесь величину достоверности уже нельзя считать удовлетворительной.

4.7 Полиномы второй степени

$y=\text{a}x^2+bx+c.\mspace{72mu}(24)$

В соответствии с формулой (1) получаем:

$\sum_{i=1}^{N}{\left[y_i-\left(\text{a}x_i^2+bx_i+c\right)\right]^2\rightarrow min}$

В таком случае согласно (5) получаем систему уравнений:

$\left\{\begin{matrix}\sum_{i=1}^{N}{\left[\left(\text{a}x_i^2+bx_i+c-y_i\right)x_i^2\right]=0}\\\sum_{i=1}^{N}{\left[\left(\text{a}x_i^2+bx_i+c-y_i\right)x_i\right]=0}\\\sum_{i=1}^{N}{\left(\text{a}x_i^2+bx_i+c-y_i\right)=0}\\\end{matrix}\right.,$

выполнив преобразования, получаем:

$\left\{\begin{matrix}\text{a}\sum_{i=1}^{N}{x_i^4+b\sum_{i=1}^{N}{x_i^3+}c\sum_{i=1}^{N}{x_i^2=\sum_{i=1}^{N}{x_i^2y_i}}}\\\text{a}\sum_{i=1}^{N}{x_i^3+b\sum_{i=1}^{N}{x_i^2+}c\sum_{i=1}^{N}{x_i=\sum_{i=1}^{N}{x_iy_i}}}\\\text{a}\sum_{i=1}^{N}{x_i^2+b\sum_{i=1}^{N}{x_i+}cN=}\sum_{i=1}^{N}y_i\\\end{matrix}\right..\mspace{72mu}(25)$

Проще всего решить данную систему уравнений методом Крамера [4] (напомню, что неизвестными в нашем случае являются переменные a, b и с):

$\bigtriangleup = \begin{vmatrix} \sum_{i=1}^{N}x_i^4 & \sum_{i=1}^{N}x_i^3 & \sum_{i=1}^{N}x_i^2 \\ \sum_{i=1}^{N}x_i^3 & \sum_{i=1}^{N}x_i^2 & \sum_{i=1}^{N}x_i\\ \sum_{i=1}^{N}x_i^2 & \sum_{i=1}^{N}x_i & N \end{vmatrix} \mspace{24mu}\bigtriangleup_\text{a} = \begin{vmatrix} \sum_{i=1}^{N}x_i^2\cdot y_i & \sum_{i=1}^{N}x_i^3 & \sum_{i=1}^{N}x_i^2 \\ \sum_{i=1}^{N}x_i\cdot y_i & \sum_{i=1}^{N}x_i^2 & \sum_{i=1}^{N}x_i\\ \sum_{i=1}^{N}y_i & \sum_{i=1}^{N}x_i & N \end{vmatrix}$ $\bigtriangleup_b = \begin{vmatrix} \sum_{i=1}^{N}x_i^4 & \sum_{i=1}^{N}x_i^2\cdot y_i & \sum_{i=1}^{N}x_i^2 \\ \sum_{i=1}^{N}x_i^3 & \sum_{i=1}^{N}x_i\cdot y_i & \sum_{i=1}^{N}x_i\\ \sum_{i=1}^{N}x_i^2 & \sum_{i=1}^{N}y_i & N \end{vmatrix} \mspace{24mu}\bigtriangleup_c = \begin{vmatrix} \sum_{i=1}^{N}x_i^4 & \sum_{i=1}^{N}x_i^3 & \sum_{i=1}^{N}x_i^2\cdot y_i \\ \sum_{i=1}^{N}x_i^3 & \sum_{i=1}^{N}x_i^2 & \sum_{i=1}^{N}x_i\cdot y_i\\ \sum_{i=1}^{N}x_i^2 & \sum_{i=1}^{N}x_i & \sum_{i=1}^{N}y_i \end{vmatrix}$

Отсюда:

$\text{a}=∆_\text{a}/∆; b=∆_b/∆; c=∆_c/∆.\mspace{72mu}(26)$

Теперь коэффициенты a, b и c можно подставить в уравнение (24) в явном виде. А значит можем записать соответствующий SQL-запрос для построения полиномиальной зависимости второй степени (см. листинг 8).

CREATE OR REPLACE VIEW approximation AS
WITH 
  k_yval AS (SELECT MAX(yiu)                 AS max_year
                  , MIN(yiu) - 1             AS min_year
               FROM tbl_iu)
, k_stat AS (SELECT yiu::decimal - min_year  AS xi
                  , ciu                      AS yi
               FROM tbl_iu 
                  , k_yval
             )
, k_par AS (SELECT COUNT(1)                  AS cnt
                 , SUM(POWER(xi, 2))         AS sum_x2
                 , SUM(POWER(xi, 3))         AS sum_x3
                 , SUM(POWER(xi, 4))         AS sum_x4
                 , SUM(xi * xi * yi)         AS sum_xxy
                 , SUM(xi * yi)              AS sum_xy
                 , SUM(xi)                   AS sum_x
                 , SUM(yi)                   AS sum_y
              FROM k_stat
            )
, k_app AS (SELECT dlta/dlt0 as a_sqr
                 , dltb/dlt0 as b_sqr
                 , dltc/dlt0 as c_sqr
              FROM (SELECT sum_x2 * (cnt * sum_x4 + 2 * sum_x3 * sum_x - sum_x2 * sum_x2)
                         - sum_x4 * sum_x * sum_x - cnt * sum_x3 * sum_x3             AS dlt0
                         , sum_xxy * (cnt * sum_x2 - sum_x * sum_x)
                         + sum_xy * (sum_x * sum_x2 - cnt * sum_x3)
                         + sum_y * (sum_x * sum_x3 - sum_x2 * sum_x2)                 AS dlta
                         , sum_xxy * (sum_x * sum_x2 - cnt * sum_x3)
                         + sum_xy * (cnt * sum_x4 - sum_x2 * sum_x2)
                         + sum_y * (sum_x2 * sum_x3 - sum_x * sum_x4)                 AS dltb
                         , sum_xxy * (sum_x3 * sum_x - sum_x2 * sum_x2)
                         + sum_xy * (sum_x2 * sum_x3 - sum_x * sum_x4)
                         + sum_y * (sum_x2 * sum_x4 - sum_x3 * sum_x3)                AS dltc
                      FROM k_par
                   ) t1
              )
SELECT x_year                                AS x_year
     , y_real                                AS y_users 
     , k_app.a_sqr                           AS a_sqr
     , k_app.b_sqr                           AS b_sqr
     , k_app.c_sqr                           AS c_sqr
     , x * x * k_app.a_sqr
     + x * k_app.b_sqr                      
     + k_app.c_sqr                           AS y_approximation
  FROM (SELECT CASE 
                 WHEN x_year < 0 THEN max_year - x_year - k_yval.min_year 
                 ELSE x_year - k_yval.min_year
               END AS x
             , y_real
             , CASE WHEN x_year < 0 THEN max_year - x_year ELSE x_year END AS x_year
          FROM (SELECT yiu AS x_year
                     , ciu AS y_real
                  FROM tbl_iu
                 UNION ALL
                SELECT -1 * ROW_NUMBER() OVER (ORDER BY yiu) AS x_year
                     , NULL AS y_real
                  FROM (SELECT UNNEST(STRING_TO_ARRAY(LPAD('', 5-1, ','), ',')) AS yiu) AS t0
               ) t1
             , k_yval
         ORDER BY x_year
       ) t_in
 CROSS JOIN k_app
 ORDER BY x_year

--                                 Листинг 8
-- Набор точек, соответствующих полиномиальной аппроксимации 2 степени.

Результаты, полученные таким образом, представлены на рис. 9:

Рис. 9Аппроксимация полиномом второй степени y = ax2 + bx + c построенная на основе листинга 8. — Рис. 9
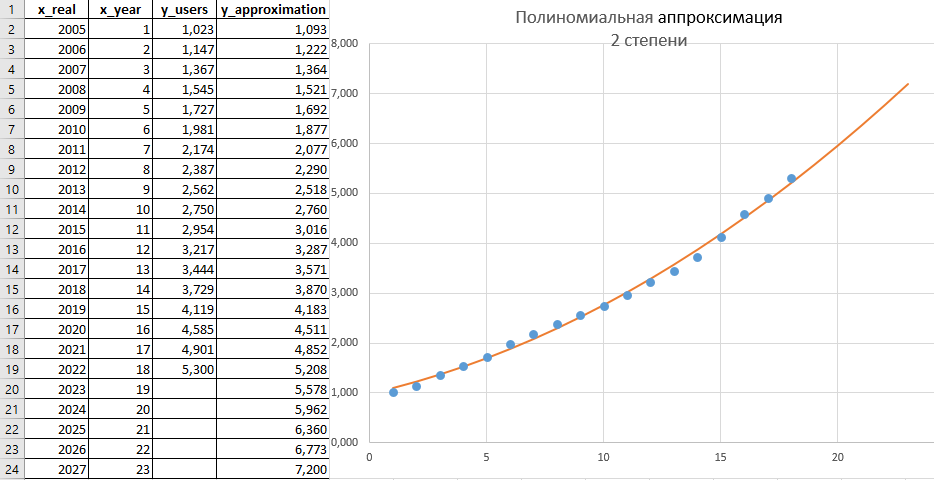
Аппроксимация полиномом второй степени *y = ax² + bx + c* построенная на основе листинга 8.

В расчете (листинги 8 и 2) были получены следующие численные значения: a_sqr = 0,0071; b_sqr = 0,1070; c_sqr = 0,9791; R²= 0,9962, и это лучший вариант аппроксимации, который удалось получить. Здесь стоит сказать, что можно было бы выполнить аналогичные расчеты для полиномов более высокого порядка, так как принципиальных сложностей с их решением нет. Однако, такие расчеты были бы существенно более громоздкими, чем в случае полинома второй степени. Здесь ограничимся просто констатацией того, что SQL подойдет и для работы с аппроксимацией полиномами более высокого порядка. Стоит отметить, что при увеличении степени полиномиальной аппроксимации можно получить такой результат, когда более высокая степень полинома лучше решает задачу интерполяции (т.е. теория ближе к экспериментальным точкам), но при этом существенно хуже подходит для расчета линии тренда на будущие периоды. Аппроксимация по определению есть некое приближение – попытка заменить сложные зависимости относительно простыми математическими моделями. Здесь важно избегать излишнего усложнения.

4.8 Краткие результаты

Аппроксимация	Функция	a; b; c	R²	Результат
Линейная	y = ax + b	0,242; 0,529	0,978	отличный
Экспоненциальная	y = a∙exp(b∙x)	1,051; 0,093	0,990	отличный
Степенная	y = a ∙ x ^b	0,755; 0,599	0,907	хороший
Логарифмическая	y = a + b ∙ ln(x)	-0,095; 1,446	0,788	средний
Обратная	y = 1 / (a + b∙x)	0,836; -0,041	-0,112	плохой
Гиперболическая	y = a + b/x	3,550; -3,718	0,435	плохой
Полиномиальная второй степени	y = ax² + bx + c	0,007; 0,107; 0,979	0,996	лучший

Из всех рассмотренных нами аппроксимаций, наилучший результат показала аппроксимация, выполненная на основе полиномов второй степени. Судить о степени совпадения с эмпирическими данными правильней всего, основываясь на величине коэффициента достоверности. Напомним, что хорошим результатом принято считать такой, у которого R² более 0,8. Процесс аппроксимации можно автоматизировать, выбирая тот вариант аппроксимации, который показал лучший результат. Данный подход хорош тем, что в процессе наблюдения за экспериментальным результатом по мере поступления данных может оказаться так, что один вид аппроксимации придется заменить на другой. Так резкий рост числа пользователей интернета (который как раз мы рассматриваем) не будет продолжаться долгие годы. Очевидно, что со временем число пользователей перестанет увеличиваться столь стремительными темпами, а следовательно и вид аппроксимаций тоже изменится.

5. Hadoop

Поскольку Postgres/GreenPlum и Hive несколько по-разному смотрят на преобразования типов, то при переходе к Hive придётся внести некоторые изменения в синтаксис. Так, к примеру, SELECT 1 / 2 = 0 (версия PG) и SELECT 1 / 2 = 0,5 (версия Hive). Таком образом, в Hive нет необходимости явно выполнять преобразование типов (пункт 1, листинг 9). Цифра 5 (пункт 2, листинг 9) отвечает за продолжительность прогноза на перспективу (в нашем случае – это пять лет).

Ниже представим изменения выполненные в соответствии с синтаксисом Hive:

1)
--GREENPLUM
SELECT yiu::decimal - min_year

--HIVE  
SELECT yiu - min_year


2)
--GREENPLUM
SELECT UNNEST(STRING_TO_ARRAY(LPAD('', 5-1, ','), ',')) AS yiu

--HIVE  
SELECT EXPLODE(SPLIT(LPAD('', 5-1, ','), ',')) AS yiu

--                              Листинг 9
-- Изменения в синтаксисе запросов при переходе к Hive.

6. Выводы

Для демонстрации представленных результатов нам потребовалось совсем немного: таблица с результатами измерений, возможность писать SQL-запросы и Excel в качестве BI-инструмента. Возможностью отображать результаты на дашборде, используя SQL-запросы, обладают такие известные BI-инструменты как Grafana, Power BI и другие. При таком выборе визуализации полученных результатов (линий тренда) достаточно перенести аппроксимирующий запрос в сам BI-инструмент, собственно задача на этом будет решена.

Выбор аппроксимирующей функции должен осуществляться на основе вычисленных параметров, наиболее близко описывающих функциональную зависимость между изучаемыми величинами. Таким образом, если есть несколько подходящих вариантов аппроксимирующих функций, нужно выбрать ту функцию, которая предоставляет большую величину достоверности R².

Представленное количество функций для аппроксимации, конечно, не является полным набором всех возможных вариантов. Это наиболее распространённые и вместе с тем наиболее простые способные аппроксимировать непериодический набор экспериментальных результатов. Используемый здесь метод наименьших квадратов хорош тем, что предоставляет готовую теорию, которую можно использовать для разных типов аппроксимирующих функций. А значит вы можете сами добавить ту функцию, которая по вашему мнению могла бы описать функциональную зависимость лучшим образом, если вас не устроят те, что уже представлены в статье. Для этого вам придется проделать аналогичные вычисления, после чего оценить успешность проделанной работы, рассчитав коэффициент достоверности R².

Увы, МНК имеет некоторые существенные ограничения: во-первых, погрешность отдельного измерения здесь никак не учитывается, во-вторых, метод не способен учитывать возможную систематическую ошибку, а в-третьих, его применение обосновано лишь при достаточно большом количестве экспериментальных результатов. Действительно, набор точек (x,y), что были получены из эксперимента, неизбежно содержат ошибку измерений, шум, выбросы и т.д. При большом наборе исходного материала (большое количество измерений) можно выполнять интегрирование входящих параметров, уменьшая влияние ошибок на конечный результат. Для этих целей может быть применена оконная функция AVG(x) over (PARTITION BY mygroup) где mygroup – группа точек за некоторый промежуток (за неделю, месяц, квартал и т.д.).

Сложность и многообразие процессов функционирования реальных систем не позволяют получить абсолютно адекватные математические модели. Математическая модель, описывающая формализованный процесс функционирования системы, в состоянии охватить только основные характерные закономерности. От аппроксимации разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все экспериментальные точки. То есть процесс аппроксимации заключается в построении приближенной функции. Исследователь вынужден руководствоваться лишь собственной интуицией, опираясь на постановку прикладной задачи и понимание природы процессов
функционирования системы.

Источники

Автор статьи: Константин Скибинский, ведущий консультант центра компетенций Big Data Solutions в компании Neoflex

Комментарии (6)

Akina
11.12.2023 09:49
#26253448
Сильно удивлён используемым видом уравнения регрессии для степенной функции (формула 12). Нет, вот какой смысл аппроксимировать функцию, которая имеет точку, подозрительно напоминающую (0, 1), используя аналитическую функцию, которая ни при каких обстоятельствах через эту точку не проходит? зато гарантированно проходящую через точку (0, 0), которой в показанной зависимости и не пахнет... Что мешает ввести постоянный член? можно даже принудительно - единицу, это уже должно значительно улучшить результат.

Что же до "гиперболической функции" (формула 21), то тут я вообще не понял, что в этой формуле было найдено гиперболического. Ну и опять же, пройти в районе точки (0, 1) функции показанного вида явно не светит.
1. neoflex Автор
  11.12.2023 09:49
  #26254706
  Добрый день! Рассмотренная в статье зависимость (количество Интернет-пользователей от времени) – это всего лишь один из возможных примеров. Предложенный вариант решения носит универсальный характер, то есть подходит под любой пример. По этой причине рассматриваются все варианты аппроксимации, даже если они заведомо плохо описывают конкретный пример (есть вероятность, что другой пример опишет как раз та аппроксимация, которая не дала хорошего согласия в нашем случае). Вариант степенной регрессии записан в виде y=ax^b. Надо понимать, что мало записать функцию произвольного вида, следующим шагом необходимо решить уравнения методом МНК, а это накладывает существенные ограничения. Не каждая система уравнений может быть решена аналитически. Как раз это и мешало добавить дополнительное слагаемое - с в уравнение (добавить можно, но решить нельзя). Для улучшения аппроксимации можно переопределить систему координат, и об этом говорится в статье. График функции 21 - y=b/x – это гипербола.
  1. Akina
    11.12.2023 09:49
    #26254820
    К слову, вынужден напомнить.
    
    Вы используете замену переменных. При этом получаете аппроксимацию по МНК для именно заменённых данных - но при этом, скорее всего, найденное значение вовсе не будет МНК-минимумом для исходных данных без замены. И чем "кривее" замена, тем больше "вес" отклонений на одной стороне по сравнению с другой, и тем больше разница между оптимумом, полученным с заменой, и полученным без неё.

ptr128
11.12.2023 09:49
#26254068
Если вспомнить, что в PostgreSQL в качестве процедурного языка можно использовать R или Python, а параметры могут быть массивами, то можно воспользоваться уже готовыми пакетами этих языков, вместо изобретения велосипедов на SQL. Причем если простые аппроксимации закодировать на SQL хотя бы реально, то более сложные периодические модели - уже не очень. Да даже просто читать код вычислений на R или Python легче, чем на SQL.
1. neoflex Автор
  11.12.2023 09:49
  #26254756
  Добрый день! Верно, задача аппроксимации может быть решена с использованием сторонних библиотек. R или Python как раз те языки, где есть библиотеки, предоставляющие такие решения. Если вас больше устраивает такой вариант, конечно, им можно пользоваться, тем более, что вам ближе R или Python, чем SQL. Но стоит остановиться на ряде недостатков такого подхода:
  
  1) SQL-решение может быть (возможно, с небольшими доработками) перенесено практически на любой тип базы (Oracle, MS SQL, SAP и т.д.). Возможно ли его так же легко перенести со сторонними библиотеками? Скорее – нет;
  
  2) Производительность – не самая сильная сторона R или Python. Сможет ли ваше решение работать с такой же производительностью, как SQL-запрос? Здесь могут быть сомнения;
  
  3) Установка дополнительных библиотек – не всегда простая задача. Если вам доводилось работать в крупных организациях, то на согласование и установку библиотек уйдут месяцы;
  
  4) По поводу того, что нельзя/сложно апроксимировать периодическую функцию: ряд Фурье считается SQL-ем практически так же, как и другим языком;
  
  5) Какой код легче читать – здесь, как нам кажется, дело вкуса и привычки.
  1. ptr128
    11.12.2023 09:49
    #26255126
    1) На MS SQL тоже самое доступно через sp_execute_external_script() или через CLR. Hana и Oracle я знаю поверхностно, но сомневаюсь, что они лишены подобных интерфейсов.
    
    2) Что касается производительности, то тут Вы лукавите. Математические пакеты и в R, и в Python, пишут на C/C++ и сами языки выступают лишь связкой между вызовами. Да и не сказал бы, чтобы производительность plpgsql была выше, чем у plr или plpythonu.
    
    3) Мне доводилось внедрять в очень крупных организациях. Именно поэтому я поставил на первое место R, так как для Python есть только небезопасный plpythonu. Для R же все намного проще согласуется.
    
    4) Я имел в виду намного более сложные аппроксимации. Например, восстановление пропусков фильтром Калмана по сезонной модели ARIMA.
    
    5) SQL не предоставляет удобных способов присвоения переменной значения и использование значений этой переменной в одном и том же запросе. Костыли в виде функций или CTE и читаются хуже, и на производительность влияют не лучшим образом. Отсюда и громоздкие повторяющиеся выражения. Все же математические выкладки лучше вписываются в императивное представление, чем в декларативное.