Общая концепция

Основа работы игровой физики, как и игры в целом, является дискретность, то есть разбиение по кадрам. В случае с графикой мы стремимся как можно чаще рисовать кадр, чтобы игра была более плавной. Но в случае с физикой обычно стремятся к фиксированному времени кадра, в угоду стабильности. Обычно обновление физического мира происходит 60 раз в секунду.

На кадре происходит расчет взаимодействия объектов, а затем до следующего кадра все двигается так, как будто нет никаких препятствий.

Уже из этого ограничения вытекают проблемы. Кажется что 1/60 секунды - это довольно маленькое время (17 миллисекунд, если быть точным), однако в мире физики может случиться многое. Например, пуля, летящая сквозь тонкую стенку. Один кадр она с одной стороны стенки, а следующий кадр уже с другой. С точки зрения дискретной физики между ними не было контакта и пуля летит дальше.

Справедливости ради обычно пули так в играх не делают, применяют трассировку луча. Или используют другие подходы в обнаружении столкновений (об этом позже).

Однако это фундаментальное ограничение игровой физики, которое ограничивает точность работы. Нельзя ожидать что физика в играх будет точно такой же как в реальной жизни, и дискретность - это ключевое ограничение.

Для симуляции используются 2 основных подхода, применяющиеся на практике: это физика твердых и мягких тел. Разберем каждый из них.

Физика твердых тел

Как и следует из названия, основой этого подхода являются твердые тела, которые двигаются в пространстве, имеют некую оболочку (или коллайдер), взаимодействуют друг с другом и не могут деформироваться. При столкновении тела обмениваются импульсами, и на них могут воздействовать сторонние силы, например гравитация.

Последовательность симуляции

Рассмотрим что происходит на каждом кадре обновления симуляции по шагам:

• Шаг 1: интегрирование. Двигаем тела в соответствии с их скоростями

• Шаг 2: поиск столкновений. Ищем какие тела столкнулись, какие точки контакта

• Шаг 3: разрешение контактов. Считаем и применяем импульсы в местах контакта, а так же в других ограничениях, напр. в джоинтах (чуть ниже)

• Шаг4: применение сил. Применяем сторонние силы, например гравитацию, аэродинамику и другие игровые фичи

На следующем кадре все шаги повторяются.

Параметры тела

Рассмотрим параметры тел, которыми оперирует физика твердого тела (rigid body):

• трансформация в пространстве. Матрица или вектор + кватернион. Описывают позицию центра масс и ориентацию тела в пространстве.

• линейная и угловая скорости. Описывают с какой скоростью в текущий момент движется тело, и с какой скоростью крутится относительно центра масс.

• масса. Общая масса тела, для расчета импульса

• инерция и момент инерции. Физические величины, показывающие насколько сложно сдвинуть и закрутить тело соответственно

• тип тела. Определяют может ли это тело двигаться от взаимодействия с другими объектами.
  

  • Статическое тело не движется никогда. С его помощью делают, например, землю.

  • Динамическое движется и взаимодействует с другими телами. Это обычные движущиеся тела.

  • Кинетическое - что-то среднее между статическим и динамическим: оно может двигаться и иметь скорость (например от анимации), но другие тела не могут повлиять на него. Используется, например, для движимых платформ.

• набор коллайдеров. Определяют форму объекта, его границы, как оно будет сталкиваться с другими телами. Имеют параметры плотности, коэффициенты отскока и трения. Коллайдер как правило один, но для сложных форм может быть скомбинировано несколько.

Шаг 1: интегрирование

Итак, у нас есть тела, в физическом мире их может быть множество. Со временем они меняют свое положение в зависимости от скоростей.

На этом шаге рассчитывается новые трансформации тел на основе текущих скоростей. На предыдущем кадре мы их как-то посчитали, и на этом шаге применили их - подвинули трансформации так, как будто они летели 1/60 секунды без каких-либо препятствий. Кроме линейного движения так же они крутятся в зависимости от угловой скорости.

position = position + velocity * delta_time;

На этом же шаге объекты могут засыпать и замирать. Это оптимизация для тех объектов, которые почти или совсем не двигаются. Для них не происходит интегрирование, не пересчитываются столкновения. Это сильно экономит ресурсы, т.к. обычно на сцене большинство объектов "спит" без движения, пока их не коснутся движущиеся объекты и не разбудят.

Шаг 2: Поиск столкновений

Теперь, когда тела заняли свои новые позиции, нужно проверить не столкнулись ли они. Для этого проверяем их коллайдеры на предмет пересечений. Нам необходимо узнать не только факт того что они пересеклись, но и получить довольно подробную информацию как именно:

• точки контакта (P). Одна или несколько точек в пространстве, описывающие площадь контакта

• нормаль контакта (N). Фактически описывает в каком направлении одно тело приникло в другое. Для плоскости нормаль будет перпендикулярна этой плоскости. Для сферы направлена наружу, по направлению от центра к точке контакта на границе сферы.

• глубина проникновения (H). Это расстояние, на которое необходимо раздвинуть объекты вдоль нормали контакта, чтобы они перестали пересекаться. Грубо говоря, насколько один коллайдер залез в другой.

• идентификаторы точек контакта. Между разными кадрами мы должны уметь понимать что коллайдеры продолжают соприкасаться в конкретных точках. Это необходимо для стабильных расчетов импульса, об этом будет позже

• параметры коллайдеров. Коэффициенты отскока и трения.

Как найти эти точки контакта? Эта задача довольно сложная, и в игровой физике это одна из самых сложных задач.

Во-первых, объектов много. На сцене может быть запросто несколько сотен тел. Для каждой пары тел необходимо проверить не пересекаются ли они, а это огромное количество проверок. Во-вторых, сама проблема поиска точек контакта - весьма сложная математическая и алгоритмическая задача.

В целях оптимизации шаг поиска столкновений делится на 2 части: широкая и узкая фаза.

Широкая фаза

В широкой фазе мы отсеиваем пары тел, которые точно не пересекаются, с помощью грубых проверок. Для этого есть несколько подходов:

• axis aligned bounding box (AABB). Мы можем посчитать в какой объем по всем осям помещается вся геометрия коллайдера. Далее с помощью весьма простых условий мы можем понять что AABB двух коллайдеров не пересекаются и быстро отсеивать явно не пересекающиеся тела

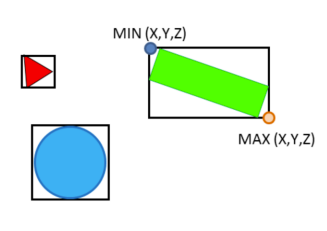
if (first.xMax < second.xMin || first.xMin > second.xMax || 
    first.yMax < second.yMin || first.yMin > second.yMax || 
    first.zMax < second.zMin || first.zMin > second.zMax) 
{ return false; }

Вместо AABB можем использовать и другую геометрию, например сферы. Их проверка тоже довольно простая

if (distance > first.radius + second.radius) { return false; }

• различные способы разбиения пространства. Если объекты в разных секторах, то можно не проверять их пересечение

  

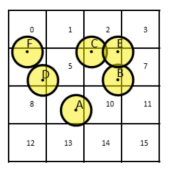
• сортировка по оси. Сортируем все объекты по какой-то из осей мира (или нескольким). Далее по ней же грубо проверяем что объекты точно не пересекаются и отсеиваем их

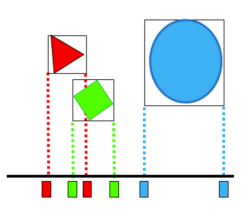
В современных движках эти подходы комбинируются.

В итоге мы за счет более простых проверок пересечения отсеиваем основную массу явно не пересекающихся тел, значительно уменьшая нагрузку.

Узкая фаза

В этой фазе мы проверяем реальные коллайдеры на пересечение и ищем точки контакта.

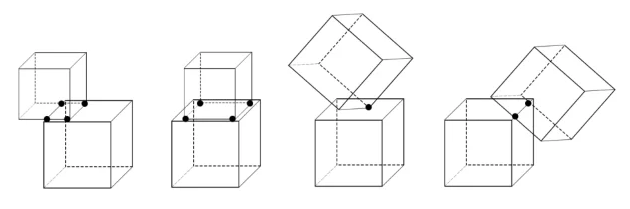
Возьмем самый очевидный пример: проверка пересечения двух мешей. Каждый меш - это набор треугольников. Для графики мы тоже их используем при отрисовке, почему бы не использовать их для проверки пересечения?

Однако, это самый сложный случай проверки пересечения. Ведь по факту нам нужно перебрать каждую пару треугольников и проверить не пересекаются ли они. Здесь мы получаем ту же самую проблему с количеством проверок, как описано выше про количество тел. Так же выплывает множество нюансов, таких как общие ребра между треугольниками. Все это сильно усложняет проверку пересечения двух мешей.

Так же использовать такие же меши что и в рендере - весьма плохая затея из-за избыточности. В графике могут быть использованы модели с десятками тысяч треугольников, и проверка пересечения двух таких мешей крайне затратна. К тому же, в физике не нужна такая точность, и даже наоборот, более грубые коллайдеры ведут себя лучше и более предсказуемо: они не цепляются острыми краями, получается меньше точек контакта и точность расчета импульсов повышается.

Гораздо лучше себя показывают упрощенные геометрические фигуры: сферы, боксы, цилиндры, капсулы и т.п. У них есть простое математическое описание и понятные алгоритмы проверки пересечения. Правда, для каждой пары типов геометрий нужна своя отдельная функция проверки пересечений.

Лучше всего в проверке пересечения в узкой фазе показывают себя выпуклые фигуры. Они описываются несколькими гранями и вершинами, и всегда образуют выпуклую геометрию. Для них есть простой алгоритм проверки пересечения - теорема разделяющей оси. Она гласит что два замкнутых выпуклых объекта не пересекаются, если существует линия («разделяющая ось»), на которой не пересекаются проекции двух объектов.

Для каждой грани мы получаем нормаль, проецируем на нее обе фигуры, и если хотя бы по одной оси пересечений нет - значит фигуры не пересекаются. В качестве нормали берем ту ось, на которой пересечение минимальное. Глубина проникновения - это пересечения проекций. Точки контактов строятся как пересечение плоскостей фигур, лежащих перпендикулярно разделяющей оси.

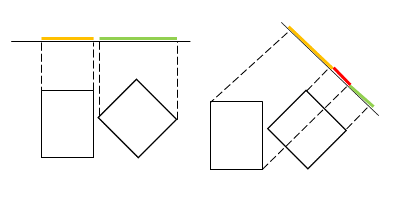
Сложные фигуры можно составлять из нескольких выпуклых фигур. Любой меш можно разбить на несколько выпуклых фигур и скомбинировать между собой. Для физики не важно что геометрия описана несколькими фигурами, важно получить список контактов.

Continous Collision Detection

Вспомним пример с пулей, которая быстро пролетает сквозь стенку. Предыдущий кадр она с одной стороны, на следующий кадр с другой. Классический подход не даст нам точек контакта и пуля пролетит сквозь стенку.

Для решения этой проблемы используются другие алгоритмы проверки столкновений, который учитывает предыдущее положение коллайдера на прошлом кадре. В таком случае мы поймем что коллайдер пули на самом деле пересекается со стеной.

Однако, такой подход значительно более затратен и сложнее. При этом в большинстве ситуаций фактически он не нужен, ведь скорости большинства объектов не такие большие. Как правило физические движки позволяют комбинировать оба подхода. Поэтому стоит включать такой режим точечно, только по необходимости.

"Застрять в текстурах"

Здесь как раз и можно объяснить этот термин. На самом деле ни в каких текстурах конечно же ничего не застревает, по сути это понятие противоречит логике. Текстура - это картинка, которая в рендере натягивается на меш, определяющая как он выглядит. Застрять в текстуре, это что-то вроде как застрять в кино или в картинке, но никак не имеет отношения к физике.

На самом деле застревание происходит в коллайдерах, когда объект попадает между составными частями коллайдеров объекта. Классический пример: регдолл (ragdoll, симуляция трупа) где-то застревает и начинает неестественно болтаться. Просто его разные коллайдеры застревают по разные стороны других коллайдеров, из-за того что они слишком глубоко пролезли друг через друга.

Шаг 3: Разрешение контактов

Теперь у нас есть информация о том, кто с кем и как пересекся в физическом мире. Сейчас важно сделать так, чтобы после контактов тела повели себя физически правдоподобно. Фактически нам нужно обновить скорости всех тел, чтобы проинтегрировать их на следующем кадре.

Все контакты рассматриваются как ограничения:

• проникновение тел должно быть нулевым

• суммарный импульс должен сохраниться

Фактически нам нужно решить систему ограничений, образованных множеством контактов. Часть физического движка, отвечающая за решение контактов, называется солвер (solver).

В физике твердых тел применяется подход с импульсами. Тело может контактировать с множеством других тел, но взаимодействия между ними рассматриваются попарно и последовательно. Для каждой точки контакта мы рассчитываем суммарный импульс столкнувшихся тел, применяем коэффициенты трения и отскока, и прикладываем обратную импульс к объектам, в зависимости от их масс.

// Скорость тел в точке контакта:
(A)  rel_a_velocity = A.velocity + (contact_point - A.position) ^ A.ang_velocity
(B)  rel_b_velocity = B.velocity + (contact_point - B.position) ^ B.ang_velocity

// Относительная скорость тел в точке контакта
rel_velocity = rel_a_velocity - rel_b_velocity

// Проекция скоростей
proj_velocity = rel_velocity * contact_normal = 0

Проблемы

Однако, есть нюансы. В целом если просто посчитать импульсы и применить их, поведение выглядит правдоподобным. Но если происходит какое-то продолжительное взаимодействие, например объект лежит на земле, или еще хуже целая стопка, то система становится не стабильной и совсем не похожа на реальную жизнь.

Не стабильной она оказывается из-за того что объекты обновляют свое положение с неким промежутком времени, за который может много чего поменяться. Так же в сложных ситуациях, когда множество тел взаимодействуют друг с другом, импульсы между ними направлены в разные или даже противоположные стороны, итоговые скорости получаются совсем далекие от реальности и вся система расползается или вовсе взрывается. Наверняка вы видели такие глитчи в играх, особенно старых.

Так же есть проблема взаимопроникновения. За отведенный промежуток времени интеграции тела успеют немного влететь друг в друга (или даже совсем не немного), и приходится их "расталкивать". Для этого иногда применяют подход с дополнительным увеличением импульса, чтобы вытолкнуть объекты друг из друга. Однако, при большой глубине проникновения импульс может получиться слишком большой и объект вылетит с неестественной скоростью. Думаю, такое тоже многие наблюдали в играх.

Может начать проявляться эффект дрожания (jittering). Это когда на одном кадре считается излишний импульс, на следующем кадре объект "пролетает" свое стабильное положение, что порождает излишний импульс в другом направлении, и таким образом объект зациклено дрожит в из кадра в кадр.

К сожалению такой наивный подход с импульсами дает довольно посредственные результаты и такая физика подойдет разве что для простого бильярда.

Численные методы

Суть проблемы в том, что в системе оказывается много противоречащих ограничений. Накладывается еще и дискретность мира.

Чтобы корректно решить эту систему, недостаточно просто посчитать импульсы в моменте и применить их к скоростям. Нужно решить целую систему уравнений, где каждый контакт - это ограничение. С большим количеством объектов такие системы уравнений оказываются довольно громоздкими.

Для решения таких систем существуют численные методы. Это способ решения математических уравнений не аналитически, когда мы решаем его и находим правильный ответ, а итерационно приближаем результат к корректному. То есть итерация за итерацией, мы все точнее и точнее получаем решение системы уравнений.

Такой подход гораздо проще, чем аналитический, и он применен в игровой физике.

Однако, здесь так же есть проблема. Если решать классическими методами, то мы будем работать с огромными разреженными матрицами, тратя огромные ресурсы на умножение нулей. Есть подходы по оптимизации, однако в современный физических движках применяется несколько иной способ.

В начале 2000х на конференции GDC Erin Catto показал простую демку и рассказал о своем подходе к разрешению контактов. Эта демка называлась Box2D. Да, если вы слышали, что есть такой физический движок, то вы правы, это он и есть. Он вырос из простой демки. Что же такого там было?

Во-первых, тот же самый итерационных подход к решению ограничений. Суть сводилась к тому, чтобы считать импульсы и применять их к скоростям несколько итераций за кадр (около 6-8). При этом не считая импульс с нуля каждый кадр, а со значения импульса на предыдущем кадре. Именно для этого нужна идентификация точек контакта между кадрами.

Во-вторых, для решения проблем взаимопроникновения, использовались отдельные псевдо-импульсы и псевдо-скорости, направленные только на выталкивание тел. После интеграции, в отличие от обычной скорости, эти скорости обнуляются. Таким образом объекты выталкиваются друг из друга, но не улетают в космос.

И это дало замечательный результат! Физическая симуляция стала стабильной, даже самые сложные сцены вели себя корректно и не разъезжались. Классический стресс-тест физического движка - это пирамидка или кирпичная стенка. В ней физика должна быть очень точна, т.к. малейшая дестабилизация, и все кирпичики валятся. С ней такой подход справляется на отлично.

Трение

До сих пор мы не коснулись важной темы - трения. Но тут на самом деле все просто. Трение считается тоже через импульсы, но направленные перпендикулярно нормали контакта. Так же применяется коэффициент трения.

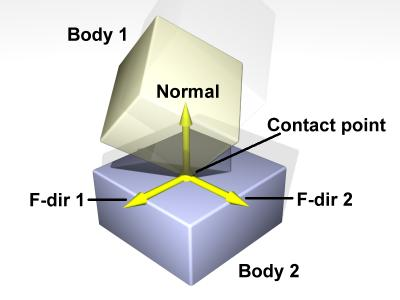
Соединения тел или джоинты

Некоторые объекты могут быть связаны друг с другом с помощью специальных соединений. С их помощью делаются, например, двери, система рычагов подвески автомобиля, подвижные части техники, симуляция тела (ragdoll)

Работают они так же через импульсы. Задаются ограничения свободы перемещения объектов относительно друг друга, и с помощью придания импульсов объектам движок пытается заставить тела принять положения, удовлетворяющие этим ограничениям.

Разрешением этих условий так же занимается солвер, с использований все тех же итерационных методов.

Джоинты могут разрушатся при преодолении некого заданного усилия. С помощью этого делаются разрушаемые объекты: они делятся на предзаготовленные части и распадаются при достижении неких усилий.

Шаг 4: Применение сил

На этом шаге применяются сторонние силы, например гравитация или другие силы, обусловленными игровыми механиками.

Здесь может быть рассчитана аэродинамика. Или взрывы от гранат: в определенном радиусе от центра взрыва ко всем телам прикладывается сила, пропорциональная удалению от центра.

В общем, здесь задается какое-то внешнее влияние на объекты через силы, которые прикладываются и обновляют скорости объектов.

Итого

Итак, мы разобрали как работает физика твердых тел. Этот подход чаще всего используется в играх и есть несколько распространенных физических движков, использующих этот подход: PhysX, Havok, Bullet, Box2D.

К плюсам можно отнести простоту понимания использования таких движков, достаточную точность для игр, и приемлемые затраты на симуляцию.

Минусом можно назвать саму особенность физики твердых тел - они не деформируются, разрушение происходит по заранее заготовленным частям. Хотя, справедливости ради, с помощью большого количества тел и джоинтов можно делать довольно интересные симуляции разрушений.

Оптимизации

С помощью правильной настройки можно сильно сократить затраты на физический движок. Общее правило - чем меньше и чем проще, тем лучше.

Более оптимально скомбинировать несколько простых коллайдеров, чем использовать меш. Например, для лавочки использовать набор боксов. А если она еще и стоит недвижимо на земле, можно пренебречь ножками и сделать всю лавочку одним простым боксом.

Так же очень эффективно использовать коллайдеры-сферы. У них очень простая формула проверки столкновения и поиска точки контакта. Однако, из множества сфер можно собрать любую форму. Да, она будет грубой и не точной, но чаще всего этого достаточно.

Иногда можно изменять шаг времени в физическом мире. Обычно используется 60 кадров в секунду как стандарт, однако, если в игре не требуется большая точность, можно уменьшить до 45-30 кадров. Для устранения рывков можно интерполировать объекты между кадрами физической симуляции.

Так же можно уменьшать количество итераций солвера. 8 итераций дают хороший результат, но если у вас нет кирпичных стен и больших нагромождений, может быть достаточно всего 3 итераций. Да, точность будет ниже, но возможно из-за особенностей геймплея это будет не заметно.

Еще один трюк с оптимизацией связан с засыпанием тел. Можно настраивать условия засыпания - за какое время тело не должно изменить свою трансформацию более какой-то дельты. Если сделать так, чтобы тела засыпали как можно раньше, пусть даже они еще совсем немного двигаются, то можно сократить затраты на интегрирование и солвер.

Физика мягких тел

Основа этой концепции в том, что тела описываются не как единый объект, а как набор связанных между собой частиц.

Каждая частица может свободно двигаться в пространстве. Они имеют только позицию, скорость и вес, но не имеют угла поворота. Частицы соединены связями (или балками). Каждая связь соединяет 2 частицы и ограничивают расстояние между ними. По сути объектов в физическом мире как таковых нет, все в нем частицы и связи. Объекты это какие-то логические представления определенных частиц и связей.

С помощью этих примитивов можно описывать что-то гибкое, например ткань. А можно и твердые формы, например треугольник. Из треугольников можно составлять более сложные формы.

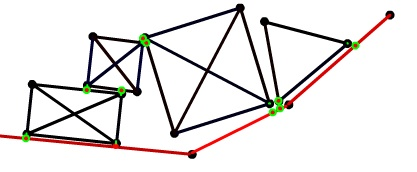
Такой подход называется физикой мягких тел потому что с его помощью принято делать что-то деформирующееся. С помощью связей можно сделать не только что-то в принципе деформирующееся, типа ткани. Связи могут так же деформироваться - разжиматься и сжиматься - за счет чего твердые структуры могут стать мягкими.

Во многом этот подход схож с физикой твердого тела, например в шагах симуляции:

• Шаг 1: интегрирование. Двигаем частицы в соответствии с их скоростями

• Шаг 2: поиск столкновений. Ищем точки контакта

• Шаг 3: разрешение контактов. Выталкиваем контактирующие частицы и ребра так, чтобы они больше не проникали друг в друга, применяем трение

• Шаг4: разрешение связей. Восстанавливаем ограничение расстояние для каждой связи

• Шаг5: применение сил. Применяем сторонние силы, например гравитация, аэродинамика и другие игровые фичи

Вершины и связи

По сути каждая частица - это точка в пространстве, движущаяся с какой-то скоростью и имеющая массу. Обычно в физике мягких тел используется интегрирование Верле, в котором нет мгновенной скорости, но есть позиция на предыдущем кадре. По сути, это некое представление скорости, которое сыграет нам на руку чуть позже.

Свойства вершины:

• текущая позиция

• позиция на предыдущем кадре

• масса

Связь соединяет 2 частицы и задает расстояние между ними:

• индекс связи 1

• индекс связи 2

• расстояние

Для более интересных эффектов могут быть добавлены коэф. упругости, пластичности и прочности.

Шаг 1: Интегрирование

Объектов как таковых у нас нет, поэтому шаг интегрирование - это интегрирование частиц. Происходит оно по простой формуле:

delta = position - prev_position;
prev_position = position;
position = position + delta;

Шаг 2: Поиск столкновений

Этот шаг максимально схож с поиском столкновений в физике твердых тел. Твердые структуры можно описывать какой-то геометрией.

Но, как правило, в физике мягких тел частиц наделяют коллайдерами-сферами, что дает правдоподобный результат. Нет проблем с тем чтобы "гнуть" геометрию вслед за деформациями. И сферы супер оптимальны для поиска столкновений с любыми другими формами.

Мы точно так же получаем всю необходимую информацию о точках, нормалях и глубине контакта.

Шаг 3: Разрешение контактов

Здесь начинается небольшая "магия". В предыдущем подходе с твердыми телами мы оперировали физическими импульсами. В теории и в этом подходе можно было бы их применить... но обычно все происходит гораздо проще.

Для применения отталкивающей силы между телами мы просто сдвигаем частицы, которые проникли в другое тело так, чтобы они больше не проникали. В случае проникновения ребер сдвигаются две вершины.

Во-первых это придает некоторую скорость частице, т.к. меняется положение относительно предыдущего кадра. А как мы разбирали выше, дельта между ними - это и есть скорость.

Во-вторых, жесткие связи толкают связанные частицы, те в свою очередь другие частицы, и в итоге все тело получает некоторый импульс.

Шаг 4: Разрешение связей

Как мы видим, соль этого подхода в связях. Которые, по сути, очень жесткие пружины. Однако и здесь не все просто.

Если сделать пружины недостаточно жесткими, то твердые тела не будут твердыми, а скорее как желе. А если сделать очень упругими, то за время кадра частицы будут улетать слишком далеко. Ведь чем жестче пружина, тем большая сила прикладывается к частицам, и тем большая скорость, а значит они улетят за 1/60 секунды слишком далеко, что породит еще большую силу. Достаточную для того чтобы система "взорвалась" за несколько кадров.

На сцену снова выходят численные методы. Их использование для решения связей предложил Thomas Jakobsen, разработчик физики Hitman: Codename 47. Он предположил, что связь - это бесконечно упругая пружина, которая за любой промежуток времени стабилизируется и приведет расстояние между вершинами в целевое. То есть не нужно считать скорости, упругость и так далее, нужно просто поставить две вершины так, чтобы расстояние между ними было таким, какое задает связь. И сделать это для всех связей итеративно 6-8 раз за кадр.

for(int j=0; j<NUM_ITERATIONS; j++) 
{
  for(int i=0; i<NUM_CONSTRAINTS; i++) 
  {
    Constraint& c = m_constraints[i];
    Vector3& x1 = m_x[c.particleA];
    Vector3& x2 = m_x[c.particleB];
    
    Vector3 delta = x2-x1;
    float deltalength = sqrt(delta*delta);
    float diff=(deltalength-c.restlength)/deltalength;
    
    x1 -= delta*0.5*diff;
    x2 += delta*0.5*diff;
  }
}

Насколько прост этот метод, настолько и эффективен. Вершин много, связей тоже много, в процессе итераций система стабилизируется и приходит в наиболее правильное положение. А учитывая что для движения частиц и объектов достаточно двигать только текущие позиции, система ведет себя физически правдоподобно.

Ключевое - правдоподобно. Ведь интегрирование положения, как вы возможно заметили, не зависит от шага времени. И при столкновениях глубина проникновения, а соответственно применяемой силы, несколько случайная. Это значит что точность такой физика далека от реальности, но все же достаточна для игр.

Трение и джоинты

По сути применяется все тот же сдвиг частиц относительно друг друга учитывая силы трения или соединения.

Шаг 4: Применение сил

Здесь все так же, если нужно приложить какое-то усилие, например гравитацию, необходимо просто сдвигать частицы на нужное расстояние

Итого

Этот подход прекрасен своей простотой и результатом. С его помощью можно делать даже более интересные эффекты, чем с физикой твердых тел. Можно симулировать ткани, растительность, разрушающиеся и пластичные объекты, а так же твердые. Это, очевидно плюсы подхода.

К минусам можно отнести точность, которая тянет максимум на "правдоподобную" и далекую от реальности.

Комбинация физики твердых и мягких тел

В современных физических движках поддерживаются оба эти подхода. Картинка выше иллюстрирует использование двух подходов: ткань сделана с помощью физики мягких тел, а сферы на ней - твердые тела.

Эти два мира вполне можно подружить, достаточно понимать места их контакта, а так же обменивать импульсы на сдвиги частиц и наоборот. Учитывая что в поиске столкновений используются одинаковые функции и подходы, сделать это относительно легко.

Мысли о развитии

В завершении хотелось бы добавить своих мыслей по поводу физики в играх. Многие вылизывают картинку добиваясь фотореалистичности, техники рендера совершенствуются от года к году. И это дает плоды, статическая картинка во многих играх весьма хороша и реалистична.

Однако, когда картинка начинает двигаться, иллюзия рассыпается. Наш мозг подмечает мельчайшие детали, которые мы порой не можем объяснить. Не хватает физичности, динамичности и большей правдоподобности. На самом деле то что мы считаем твердым, не очень-то твердое: кузов автомобиля или грузовика немного прогибается от нагрузок, а крыло самолета гнется. А предзаготовленные повреждения машин всегда заметны и ты знаешь что это фейк. Всегда интереснее видеть как игровой мир реагирует на твои действия, даже не связанные с геймплеем.

Сейчас мощностей железа достаточно чтобы делать великолепные вещи. А современные движки позволяют добавлять физичность миру парой кликов мышкой.

Мне кажется стоит чаще внедрять физичные штуки в игры. Как бы это парадоксально ни звучало, мне кажется это может дать ощутимый скачек "картинки" в играх.