Помните добрый мультик про Панду Кунг Фу и «случайности, которые не случайны», как говаривал учитель‑черепаха? Похоже он намекал на детерминизм.

В разговорной речи часто встречается понятие «случайность». Говоря более «сухим» языком — это случайное событие. Не столь важно, как правильно называть такое явление. Смысл простой — случайность с физической точки зрения подразумевает событие, которое может произойти, а может и не случиться. И всю философию тут полезно исключить.
Тогда появляется интересный вопрос. Где-то глубоко в теории, любая случайность по всей логике должна быть всё-таки детерминирована. То есть исчерпывающий набор факторов и детальное описание любого процесса должны дать возможность прогнозировать явление с высокой точностью.
Упрощу формулировку: Существование случайности описывается математически. Это событие с низкой вероятностью его существования. Дальше исходим из того, что математический аппарат настолько громоздкий, а явление настолько сложное, что мы, как это говорится "забиваем" и называем всё случайным. Хотя это просто событие с низкой, точно вычисляемой, вероятностью существования.
Отмечу, что лично моё мнение по вопросу всегда строилось на том, что любая случайность - это плохо просчитанная вероятность, где не хватает данных. Что случайность невозможна технически. Но тут на своём канале я обсуждал с уважаемым комментатором принцип работы процесса измерений в квантовом компьютере.
Квантовый компьютер использует логику эффекта наблюдателя. Относительно эффекта наблюдателя у меня тоже было чёткое мнение. Я исходил из того, что существует просто невероятное количество вариантов, которые можно подсчитать согласно методу определения вероятности. Это будет, скажем, 100 (не важно сколько точно, наверное больше), возможных сценариев. Мы "наблюдая" выберем "выпавший" как в лото.
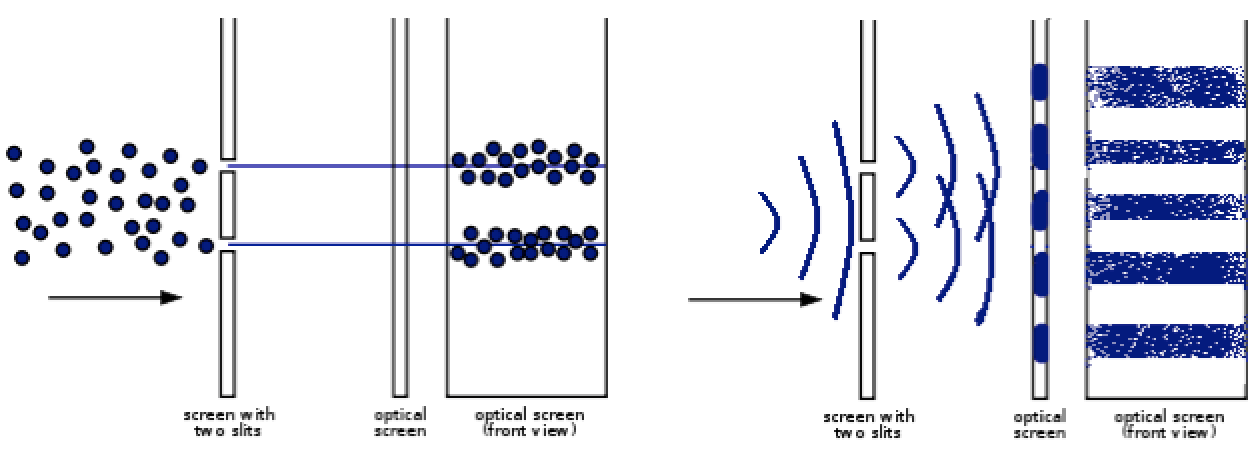
Вот только мой собеседник обвинил меня в использовании логики использования идеи "скрытых параметров". И на тот момент, я не мог представить, что случайность не детерминирована. Но такое мнение встречается мне всё чаще. Давайте попробуем ковырнуть глубже.
Случайности и точные науки
Точные науки они на то и "точные". Но возьмем, скажем, математику. Случайность, это такое событие, которое могло бы быть другим, но стало таким.
Теория вероятности делит события на три типа:
Невозможные - при данных условиях невозможны
Случайные - могут быть, а могут не быть
Достоверные - точно произойдут
Случайное событие происходит с некоторой вероятностью. События сравнивают по величине их вероятности. Например, в идеальном случае для монеты вероятность выпадения орла равна вероятности выпадения решки. И эти вероятности почти равны 0,5. Правда тут я бы "доковырялся" к этому классическому примеру и сказал, что с одной стороны монетка тяжелее, чем с другой. Значит, это точно не 0,5. Но это не суть беседы.
Как оказалось, я в своих размышлениях всегда опирался на так называемую теорию детерминизма. Она подразумевает, что если бы мы смогли запрограммировать все факторы и имели бы точное расчётное уравнение, то вычислить вероятность того или иного исхода при якобы "случайностях" не составило бы никакого труда. Причём, точность была бы 100%.
Эту логику "кроют" эффектом бабочки.
Дело в том, что большинство дифференциальных уравнений, описывающих реальные процессы, являются нелинейными уравнениями с неустойчивыми решениями относительно начальных условий.
Это подразумевает, что вроде как "точные" формулировки уравнений меняются ещё и сами вместе с изменениями условий.
Математика тут, вроде как, точная. Однако, изобилие решений делают процесс непрогнозируемым. Скажем, этакая задача трёх тел. Правда её сегодня, вроде как, уже смогли детерминировать. Но давайте рассматривать задачу трёх тел с позиции Ньютона, у которого из вычислительных устройств были, разве что счёты (и тех, не было, если серьезно). Каждое новое движение меняет расчётное уравнение.

В науке такое явление получило название "эффект бабочки". Если бабочка махнула крылышками, то где-то прошёл ураган. Таков один из возможных вариантов. Математика "оправдывает" это тем, что решение уравнения процесса будет по экспоненте отклоняться от предыдущего решения.
Два решения с очень близкими начальными условиями очень быстро станут диаметрально противоположны.
Что же...Всё равно не убедили
И всё-таки. Хорошо, многие процессы описываются нелинейными уравнениями. Предсказать что-то в объективном понимании невозможно. Компьютеры банально не умеют работать с некоторыми числами высокой точности, где есть миллионные знаки после запятой, а всё это может сказаться при наложении факторов и сработает эффект бабочки. Пусть так.
Но любое нелинейное уравнение - это всё-таки математический инструмент. Невероятно сложно учитывать все факторы. Их невозможно подсчитать и пересчитать. Результаты отличаются взрывным образом. Но всё это точная математика.
Тут я вижу два разрешения проблемы:
Или математический аппарат в принципе не может работать с высокими точностями. Значит, сколько уравнений не составляй, где-то мы упрёмся в предел вычислений и предел точности, и числа типа 0,56565689 и 0,56565683 будут иметь сходное физическое значение
Или всё-таки всё упирается в невозможность это подсчитать, а это уже совсем другая история и вся "магия" случайности пропадает и превращается в детерминированные значения
Есть ещё один вариант, о котором не хотелось бы тут писать. Вероятно, я сам не понимаю всю глубину и сложность тем нелинейных уравнений и вижу это излишне упрощенно.
Теория говорит, что в нелинейных системах взаимодействия могут влиять сами на себя: когда воздушные потоки протекают по крыльям реактивного самолёта, поток воздуха изменяет молекулярные взаимодействия, которые, в свою очередь, изменяют воздушный поток, и так далее.
Такая петля обратной связи порождает хаос, где небольшие изменения в начальных условиях позже приводят к крайне изменчивому поведению, что делает прогнозы практически невозможными.
Вот только отругайте меня в комментариях, если так нужно. Но это не исключает точный расчёт. Пускай условия хоть трижды влияют сами на себя. Они делают это согласно закономерности. Сложно не означает "невозможно". Всё упирается в ограниченность самой математики. Но это не отменяет детерминированности случайности.
В одной из статей было отмечено, что:
Эндрю Чайлдс из Университета Мэриленда возглавил работу, в которой учёные пытаются позволить квантовым компьютерам точнее моделировать нелинейную динамику. Алгоритм его команды превратил хаотичные системы в массив более понятных линейных уравнений с помощью метода линеаризации Карлемана. Джон Т. Консоли / Университет Мэриленда
Значит, если упрощение достигнуто, то и логика видимо работает. Правда здесь же отмечено, что квантовый компьютер технически не справится со всей проблемой. Ведь это устройство, которое тоже построено на линейной логической модели и заставить его решать такие вопросы - это как заставить машину летать.
Я так понимаю, что основная и главная проблема - невозможность применить линейность для работы с нелинейностью. Вся логика принципиально другая и дело тут не в философском понимании действительности. И тут я был бы благодарен за хорошие комментарии по теме. Ведь похоже нелинейность - это не просто закономерность по экспоненте или параболе, а что-то более глубокое. По крайней мере только это может оправдать существование случайности именно в том виде, как её преподносят в статьях про эффект наблюдателя.
П.с.: Подобные вопросы я часто разбираю на своём Telegram‑канале и буду рад гостям.
Комментарии (16)

Jury_78
22.04.2024 14:45Причём, точность была бы 100%.
Может надо начать с неопределенности Гейзенберга?

Radisto
22.04.2024 14:45+6Для этого автору надо бы начать с того, что математика и физический мир - разные вещи, и формула к примеру гравитации - не гравитация, а ее модель. После этого установить границы применимости этой модели (а они часто заканчиваются намного раньше, чем математическая вычислимость этой модели), а уже затем думать. Прежде чем считать, полезно понять, что именно ты считаешь: сферический конь в вакууме часто не похож на живого жеребца Василия в некоторых стремящихся к бесконечности моментах

riv9231
22.04.2024 14:45Постарайтесь вникнуть в смысл Теоремы Белла. Вы поймёте, что речь идет не о точности вычисления, а о том, что статистика истинно случайных событий отличается от статистики событий, которые только выглядят как случайные в силу невозможности установить параметры от которых они зависят. Отличается настолько, что не выполняется конкретное неравенство, разделяющее эти случаи. Оно так и называется - неравенство Белла.

miksoft
22.04.2024 14:45Существование случайности описывается математически. Это событие с низкой вероятностью его существования.
А где можно почитать именно про низкую вероятность случайности?

Kergan88
22.04.2024 14:45Про теорему Белла уже сказали.
Про некорректные задачи - суть в том, что для них погрешность решения не зависит непрерывно (и тем более с какойто гладкостью) от исходных данных. Это значит, что вот у нас есть погрешность Х, и мы ни как не можем ее уменьшить, как бы ни повышали точность наших измерений и раасчетов. Не важно, какой знак после запятой там будет - если в начальных данных есть хоть какаято погрешность (а она всегда есть), то мы не сможем ни как посчитать точнее чем Х.

Wakeonlan
22.04.2024 14:45Границы математики для описания мира проявятся, когда число пи будет по разному выглядеть в разных расчетах. Ждём:)

smart_alex
22.04.2024 14:45И тут я был бы благодарен за хорошие комментарии по теме.
Нужны хорошие комментарии? Нет проблем — сейчас будет вам хороший комментарий :)
В физическом мире любая «сущность» имеет бесконечное количество «аспектов», учесть которые во всей полноте невозможно в принципе (если вы не Бог), то есть «расшифровать матрицу» и отличить «вероятность» от «случайности» в общем случае невозможно.
Хотя «вероятности» являются (можно сказать детерминированным) следствием физического взаимодействия всего, что составляет реальный физический мир «де факто».
Надеюсь я достаточно ясно выразил свою мысль :)

Oksenija
22.04.2024 14:45>>В физическом мире любая «сущность» имеет бесконечное количество «аспектов»
Если верить популяризатору квантовой механики Семихатову, то наоборот, квантовые сущности (объекты) "имеют" ("состоят из") строго определенное и маленького кол-ва квантовых параметров или чисел (спин, заряд и т.д.) и сущности с одинаковым набором квантовых чисел неразличимы. Текст взят из лекции Семихатова https://300.ya.ru/v_AucOkd04 И более того по Беллу, доказано, что скрытых параметров у них нет. И по Беллу доказано, как ни странно, неслучайность поведения запутанных частиц. Выше же многие комментаторы говорят что Белл доказал абсолютную случайность, хотя если читать про Белла, то наоборот доказана неслучайность, корреляция, которой не должно быть при абсолютной случайности. В самой постановке вопроса по Беллу есть деталь - для корректной работы корреляторов нужен сильный сум измерений, потому там корреляторы под 22.5 градуса или 45 в разных вариантах. При 90 и 180 - неравенство Белла неприменимо и не позволяет выявить что-то новое, доп. корреляцию отнсительно абсолютной случайности. Но шумы измерений сами по себе могут быть коррелированы например из-за виртуальных частиц....

MasterOgon
22.04.2024 14:45Практика показывает что мозг может во сне предсказать события которые вы не спрогнозируете иным способом вообще никак. Я много лет на это исследование потратил и это точно. Фишка только в том что информация во сне закодирована в ассоциативные символы которые дают ощутить эмоции событий и общий смысл, но не то как это будет на самом деле. Их можно научится разгадывать благодаря повторяющимся снам. В редких случаях когда сны более осознанны можно увидеть будущее очень точно но как правило это короткие вспышки озарения в общем массиве символического сюрреализма сна, в его конце перед пробуждением. Поэтому справедливо считать что если вы не видите причин и следствий то вы их просто не видите

mivlad
22.04.2024 14:45Кажется, примерно так «предсказывают события» и карты таро.

MasterOgon
22.04.2024 14:45Ну нет. В таро одна карта может иметь много интерпретаций. Например большой финансовый успех или много лайков или ещё что то. Во сне один символ значит один тип событий, характеристики символа значат характеристики события. Например средство передвижения- работа. Самолёт - быстрые деньги, метро- невыгодная рутина. Езда наломалась-наломалась работа. Но это лично у меня и для всех персонально надо выявлять. Как в соннике одна примета для всех вряд-ли будет работать, разве что у всех одинаковые ассоциации в подсознании.
И в случае когда значение определено это работает точно как часы в том плане что предсказанное событие становится первым событием данного типа наступившим через нное время после сна. А какие либо подробности и детали события которые идентичны реальным так же могут быть но отделить их от символов изначально трудно. Не знаю как это работает и зачем но у меня в этом больше нет никаких сомнений

Kealon
22.04.2024 14:45Математика тут, вроде как, точная. Однако, изобилие решений делают процесс непрогнозируемым. Скажем, этакая задача трёх тел.Скажем так, современная физика работает с этим очень просто. Как пример, расчёт столкновения метеорита с Землёй. Всё прекрасно считается. Фокус тут в другом.
Современная физика начинается с экспериментов Гаусса (в школе это не проходят, а на матфакультетах этот ньюанс не объясняют). Перелом произошёл в понимании измерений и расчётов. Физики фактически отказались не только от знания величины, но и от 100%-й достоверности попадания в интервал. Помните анекдот про физика и математика?
"Величина" в физике и инженерных науках, по факту, описывается функцией распределения вероятности.
Например, задача: есть две коробки с гвоздями: (500+-3)мм и (700+-4)мм
Задача: посчитать сколько будет сумма длин двух гвоздей взятых из двух коробок.
Школьник сложит величины и применит формулу расчёта погрешности для сложения da+db и получит (1200+-7) мм. Его ошибка в неучёте ограничения этой формулы и непонимании инженерного описания (a+-da). Формула в школе абсолютно верная, но имеет ограничение: "все величины 100% достоверны", а это не соблюдается, так как инженерное описание (500+-3)мм подразумевает, что величина имеет нормальное(Гауссово) распределение G(500,3). Мы видим, что в интервал (500+-3)мм попадает больше 67% но не 100%. И задача математически описывается как поиск соответствия для множеств {G(500,3) + G(700,4)} = {G(?, ?)}.
Применив формулу сложения двух нормальных распределений из теории вероятности мы получим (1200+-5) мм.
Теперь к расчёту полёта метеорита. Всё это (действительно всё, вплоть до ядерного моделирования) считается с помощью ММК (методы Монте-Карло). Выполнив множество вариантов расчётов мы получим "распределение решения" нашей задачи, и соответственно можем выделить аттракторы (попал - не попал) и их вероятности.


yeg
В квантовой физике есть теорема Белла, которая позволяет отличить истинно случайную величину от псевдослучайной, то есть зависящей от некоторых неизвестных (скрытых) параметров.
Белл показал, что никакая физическая теория локальных скрытых параметров не может воспроизвести все предсказания квантовой механики. То есть, в мире существуют процессы, которые фундаментально случайны, и случайность - их неотъемлемое свойство.
Там, правда, есть философские лазейки, в стиле того, что эта теорема не работает, если есть глобальная высшая сила, которая определяет вообще всё, включая сознание наблюдателей, и заставляет их верить в то, что они делают случайный выбор, который на самом деле не случаен.
Короче, проще допустить, что случайные процессы объективно существуют
pavel_kudinov
Меня в диспуте "случайности не случайны", теореме Белла и применимому к ней в качестве контраргумента принципу супердетерминизма смущает:
проблема "случайности не случайны" не сводится к теореме Белла. теорема Белла говорит о конкретной разновидности предопределенности - причинно-следственной связанности квантовых объектов друг с другом.
я могу привести в пример гораздо более простой тип предопределённости (ожидал именно этого от супердетерминизма, но там зачем-то приплели сознание экспериментатора):
"не причинно-следственная предопределенность". можно представить себе как заранее сгенерированный и сохранённый вовне Вселенной (или симуляции) поток истинно случайных чисел, которые подсовываются квантовым системам извне системы каждый раз, когда те должны сгенерировать "истинную" случайность внутри системы
такую не причинно-следственную предопределенность изнутри Вселенной (или симуляции) никак нельзя будет отличить от истинной случайности, тем не менее ход развития такой Вселенной (или симуляции) будет полностью заранее предопределён извне
поэтому следует различать глобальный философский вопрос "случайности не случайны" (предопределенность системы извне как таковая, не гарантирующая возможность предсказаний изнутри системы) и вопрос существования скрытых параметров (причинно-следственная предопределенность, дающая надежду на возможность предсказания изнутри системы)
Antocyan
Если поток этих псевдослучайных чисел сгенерирован заранее для всех событий вселенной - это и есть супердетерминизм. Который важен с философской точки зрения, но с научной - ни в каких экспериментах ничем не отличается от истинной случайности