первая часть
Прибыв домой, Гарднер тотчас же продемонстрировал Конвею более 20 статей, посвящённых расчёту дня недели для любой даты. Правило Льюиса Кэрролла выглядело лучше остальных. Гарднер повернулся к Конвею и сказал: «Джон, тебе необходимо разработать более простое правило, которым я смогу поделиться с читателями». И, как рассказывает Конвей, длинными зимними ночами, когда мистер и миссис Гарднер у себя дома отправлялись спать (хотя в гости к ним он приезжал исключительно летом), Конвей размышлял над тем, как сделать такой расчёт достаточно простым, чтобы его можно было объяснить среднему человеку с улицы.
Он думал над этим всю дорогу домой, и в общей комнате университета, и наконец додумался до «правила Судного дня». Для работы алгоритму требовались лишь сложение, вычитание и запоминание. Также Конвей придумал мнемоническое правило, помогавшее хранить промежуточные вычисления на пальцах руки. А для наилучшего запоминания информации о дате, Конвей прикусывает свой большой палец.
С годами Конвей научил этому алгоритму тысячи людей. Иногда в конференц-зале набирается человек по 600, вычисляющих дни рождения друг друга и прикусывающих свои большие пальцы. А Конвей, как всегда, пытается быть неразумным – он уже неудовлетворён своим простым алгоритмом. С самого момента разработки он пытается его улучшить.
Кроме своих периодических поездок к Гарднеру, Конвей писал тому длинные письма, в которых суммировал свои изыскания. Он имел обыкновение вставлять в пишущую машинку рулон бумаги (подобную той, в которую заворачивают мясо) и печатал письма, измеряя их по длине. Обычно хватало письма длиной немногим более метра, хотя рекорд, по подсчётам Гарднера, был эквивалентен 11 обычным страницам.
Обычно он начинал письма с преамбулы:
Затем он углублялся в новости по своим исследованиям, начав, допустим, со своего решения по вопросу разделения пирога, переходя на новую загадку с проводом и ниткой, а затем посвящая большую часть письма:
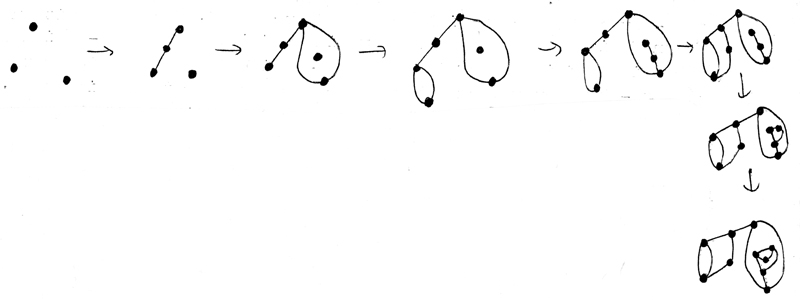
«Побеги» были изобретены совместно со студентом Майком Патерсоном и были освещены в колонке Scientific American в июле 1967 года. В ответ на письмо Гарднер отправил список вопросов, начинавшийся с вопроса «Что обозначает H в имени John H. Conway?». После каждого вопроса Гарднер оставил на листе много места, чтобы вписать ответ.
Ответ Конвея:
Гарднер также интересовался деталями происхождения игры. «Я предсказываю, что эта игра станет настолько общепринятой и известной, что для истории будут интересны детали её создания,- писал Гарднер. – Не мог бы ты рассказать о них подробнее? Ты рисовал каракули на лекции (если да, то какой?) Или за кружкой пива?»
И Конвей не останавливался. Следующее письмо было озаглавлено:
ВАЖНО! ПРОРЫВ В ПОБЕГОЛОГИИ!

Именованные позиции: мокрица, жук, таракан, серёжка, скорпион
Сегодня уже существует «Международная ассоциация игры в побеги» [The World Game of Sprouts Association], которая «посвящена изучению реальности побегов» и «серьёзному исследованию игры». Она проводит ежегодные онлайн-чемпионаты. В них могут участвовать только люди, поскольку компьютерный анализ игры за эти годы вдохновил некоторых написать ботов для игры. Конвей недавно узнал об этой ассоциации, но ему уже давно было известно о существовании компьютерных программ, играющих в игру.
В начале 90-х три учёных из Лаборатории Белла и Университета Карнеги-Меллон написали работу «Компьютерный анализ игры в побеги», в которой анализировались выигрышные стратегии вплоть до n=11. «После 11 точек их программа не смогла справиться со сложностью игры»,- писал Гарднер для своих читателей. Через пару десятилетий два французских студента, решивших побить рекорд, написали программу GLOP (в честь французского персонажа комиксов Pif le chien, говорившего glop всякий раз, когда он испытывал удовлетворение). Они защитили докторскую по этой теме, и утверждают, что нашли выигрышные стратегии вплоть до n = 44. Конвей был очень заинтересован и удивлён этим:
Ещё один пример гениальности Конвея – игра «Автомобильные пробки», в которой выдуманная страна имеет треугольную карту, а города представлены буквами. Все буквы являются первыми буквами названий реальных городов — Aberystwyth, Oswestry и Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch.
Подозреваю, что Конвей изобрёл игру только для того, чтобы лишний раз иметь возможность произнести название города Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch. Он видел его на табличке на ж/д станции и на городской площади. Интересно, что эти знаки отличались на одну букву. А что касается игры, то её вопрос был – какой первый шаг должен сделать игрок?
В игре «Пробки» четыре игрока начинают с Aberystwyth (A), Dolgellau (D), Ffestiniog (F) и Merioneth (M). Они по очереди передвигаются по односторонним улицам между городами. Игра заканчивается, когда все игроки застревают в Conwy , из которого нет выхода. Проигрывает тот, чей ход должен был быть следующим.
Все эти игры поставляли данные для теории сюрреальных чисел Конвея. Лучшими подопытными игроками были его собственные дочки, Сьюзи и Рози, 7 и 8 лет.
По счастливой случайности, в этот период (около 1970), чемпион британии по Го, Джон Даймонд, учился в Кембридже. Он основал общество Го и постоянно играл в эту игру в общей комнате. Даймонд, сейчас являющийся президентом Британской ассоциации го, не помнит, чтобы хоть раз играл с Конвеем. Конвей обычно стоял рядом, смотрел на доску и размышлял над ходами игроков.
Конвей вспоминает:
А это, в свою очередь, подвигло его на ещё большее пристрастие к играм. У него с собой всегда были все нужные аксессуары, чтобы можно было неожиданно обрушиться на соперника. В его кожаном пенале всегда были кубики, шашки, доска, бумага, карандаши, верёвка, и несколько колод карт. Карточные игры и трюки ему удавались. Его анализ игр эволюционировал от простых до составных игр, до случаев, когда игрок одновременно играл в несколько игр сразу (иногда, например, шахматы, го и игра «Domineering») – и игрок выбирал, в какой из игр ему сходить. А он заполнял бумажные рулоны анализом этих игр. Как он рассказал репортёру журнала Discover:
И всё это развивалось, чтобы в результате стать сюрреальными числами – самым большим расширением множества вещественных чисел. Название им дал компьютерный специалист из Стэнфорда Дональд Кнут. И с тех пор Конвей уже не беспокоился о трудоголике профессоре Фрэнке Адамсе и о том, чтобы угодить ему и его коллегам. Он понял, что это открытие, пришедшее из «глупых игр», относилось уже к серьёзной математике. После того, как за один период в 12 месяцев он придумал сюрреальные числа, изобрёл игру «Жизнь» и открыл группы Конвея, он принял «клятву»: «И да закончишь ты волноваться и чувствовать вину, и да будешь делать то, что угодно тебе». Он сдался своему природному любопытству, шёл туда, куда оно его вело — хоть к развлечениям, хоть к исследованиям, хоть вообще в какое-то нематематическое место.
Гарднер суммировал теорию сюрреальных чисел, как «Винтажный Конвей: глубокий, инновационный, волнующий, оригинальный, блестящий, остроумный и отличающийся Кэрролловской игрой слов. И на тривиальном фундаменте Конвей строит огромное и фантастическое здание. Но чему оно посвящено?
Конвей в работе под названием „Все числа, большие и малые“, ставит вопрос проще: есть ли польза у этой структуры?
»Она находится на границе развлечений и серьёзной математики,- говорит американский математик венгерского происхождения Пол Халмос. – Конвей понимает, что её не назовут великой, но может попытаться убедить вас, что она именно такая". Напротив, Конвей верит, что сюрреальные числа – великая вещь, безо всяких «может». Он просто разочарован, что они пока не привели к ещё более великим вещам.
И на какое место они ставят его на пути древнего интеллектуального путешествия к красоте и правде? Конвей видит себя членом оркестра на параде, марширующего по улицам времени. В топ-10 газеты Observer Конвей упомянут среди математиков, чьи открытия изменили мир. Но попробуйте обсудить с ним этот список, или же другой список, в котором он недавно нашёл себя – в книге Клиффорда Пиковера «Чудеса чисел», под названием «десять самых влиятельных математиков нашего времени»… Он сразу же возразит:
Конвей считает Архимеда отцом математики. Именно он понял вещественные числа, и был первым, рассчитавшим число ? и ограничившим его сверху 3 1?7, а снизу — 3 10?71. Но в рейтинге Observer на первом месте идёт Пифагор. Если он и не лучший, то известный более других, в основном благодаря теореме его имени. И обычно в этих списках присутствуют Эйлер, Гаусс, Кантор, Эрдёш. Конвей идёт в конце, за ним идут Перельман и Тао.
Юношеская пора Конвея пришлась на сексуальные 70-е и неумеренные 80-е. В 80-х он развёлся с первой женой и женился на математике Ларисе Куин, начав новую семью. Стал членом Королевского общества и профессором Кембриджа. А затем перевёлся в Принстон в 1987-м. Пока ещё мы слишком близко находимся к Перельману, Тао и Конвею, чтобы правильно оценить их вклад в науку – особенно, каким образом их абстрактные теории смогут пригодиться на практике. Этот анализ займёт много времени.
Интересным исключением стал Джон Нэш, коллега Конвея в Принстоне, про которого написана книга и снят фильм «Игры разума». Нэш сделал вклад в теорию игр, моментально пригодившийся в эволюционной биологии, бухгалтерском деле, политике, военной теории и рыночной экономике, что и привело к получению им Нобелевской премии по экономике. С точки зрения Конвея, работа, заслужившая Нэшу нобелевку, была менее интересной, чем Теорема Нэша о регулярных вложениях (любое Риманово многообразие можно изометрически включить в Евклидово пространство). Конвей нацелился на получение премии Абеля («Нобель для математиков»). Он выиграл кучу других призов, но с премией Абеля пока ничего не выходит.
Да и практическое приложение его работы ещё предстоит открыть. Немногие сомневаются в том, что хотя бы что-нибудь из его творений сможет найти применение. Например, сюрреальные числа. «Сюрреальные числа найдут применение,- говорит его коллега, Питер Сарнак. – Вопрос только в том, какое и когда». Сарнак вообще восхваляет Конвея. «Конвей – соблазнитель»,- говорит Сарнак, имея в виду талант Конвея как учителя и толкователя, будь то занятия со студентами, математический лагерь, лекция на частной вечеринке или его альков в общей комнате Принстона.
Его всегда можно найти в этом алькове, где он не занят работой. И хотя он надеется ещё наткнуться на другие «горячие» темы вроде сюрреальных чисел, чаще он играется с любимыми тривиальностями. Он никогда не стесняется того, чтобы поймать незнакомца и начать заваливать его своими интересами. Один из недавних – "теорема свободы воли", в которой, по его мнению, заинтересован каждый человек. Она разработана за десять лет совместно с коллегой Саймоном Коченом, и формулируется через геометрию, квантовую механику и философию. Простая формулировка звучит так: если у физиков есть свобода воли при проведении экспериментов, то она есть и у частиц. И это, по их мнению, объясняет, почему у людей вообще есть свобода воли. Это не замкнутый круг, а больше замкнутая спираль, которая поддерживает сама себя, но раскручивается и становится всё больше.
Но обычно он более всего увлечён числами. Он их поворачивает, переворачивает, выворачивает и смотрит, как они себя ведут. А более всего он ценит знание и хочет узнать всё про Вселенную. Обаяние Конвея идёт от его желания поделиться своей тягой к знаниям, распространить это увлечение и связанную с ним романтику. Он упрямо, упорно стремится объяснить необъяснимое, и даже когда оно остаётся необъяснённым, ему удаётся вдохновить аудиторию, скреплённую неудавшейся попыткой, чувствующую себя частью одной команды, удовлетворённой тем, что они смогли пофлиртовать с проблеском понимания.
Прибыв домой, Гарднер тотчас же продемонстрировал Конвею более 20 статей, посвящённых расчёту дня недели для любой даты. Правило Льюиса Кэрролла выглядело лучше остальных. Гарднер повернулся к Конвею и сказал: «Джон, тебе необходимо разработать более простое правило, которым я смогу поделиться с читателями». И, как рассказывает Конвей, длинными зимними ночами, когда мистер и миссис Гарднер у себя дома отправлялись спать (хотя в гости к ним он приезжал исключительно летом), Конвей размышлял над тем, как сделать такой расчёт достаточно простым, чтобы его можно было объяснить среднему человеку с улицы.
Он думал над этим всю дорогу домой, и в общей комнате университета, и наконец додумался до «правила Судного дня». Для работы алгоритму требовались лишь сложение, вычитание и запоминание. Также Конвей придумал мнемоническое правило, помогавшее хранить промежуточные вычисления на пальцах руки. А для наилучшего запоминания информации о дате, Конвей прикусывает свой большой палец.
Следы от зубов должны быть видны! Только так можно это запомнить. Когда я рассказываю студентам об этом методе, я всегда прошу кого-нибудь из первого ряда подтвердить наличие отметок от зубов на пальце. Серьёзных людей так делать не заставишь – они решат, что это детский сад. Но смысл в том, что всё это дело обычно не задерживается у вас в мозгу, и вы забываете дату дня рождения, названную вам человеком. Но большой палец способен запомнить за вас, как далеко эта дата отстоит от ближайшего «Судного дня».
С годами Конвей научил этому алгоритму тысячи людей. Иногда в конференц-зале набирается человек по 600, вычисляющих дни рождения друг друга и прикусывающих свои большие пальцы. А Конвей, как всегда, пытается быть неразумным – он уже неудовлетворён своим простым алгоритмом. С самого момента разработки он пытается его улучшить.
Кроме своих периодических поездок к Гарднеру, Конвей писал тому длинные письма, в которых суммировал свои изыскания. Он имел обыкновение вставлять в пишущую машинку рулон бумаги (подобную той, в которую заворачивают мясо) и печатал письма, измеряя их по длине. Обычно хватало письма длиной немногим более метра, хотя рекорд, по подсчётам Гарднера, был эквивалентен 11 обычным страницам.
Обычно он начинал письма с преамбулы:
Получил первую посылку с книгами прямо перед Рождеством, и так обрадовался, что несколько дней читал их и перечитывал, особенно «Алису» с комментариями (жена моя от тебя не в восторге!).
Затем он углублялся в новости по своим исследованиям, начав, допустим, со своего решения по вопросу разделения пирога, переходя на новую загадку с проводом и ниткой, а затем посвящая большую часть письма:
Побеги. Эту игру мы придумали две недели назад, днём во вторник. К среде весь математический департамент был ею заражён, поддались даже секретари. Начинаем с n точек на листе бумаги. Ход состоит в объединении двух точек (можно объединять точку с собой) при помощи кривой, а затем в обозначении на этой кривой новой точки. Кривая не должна проходить через старые точки, не должна пересекать старые кривые, и из одной точки не должно выходить более трёх кривых. В обычных Побегах проигрывает тот, кто не может сделать ход. В Побегах-мизер проигрывает последний, сделавший ход.
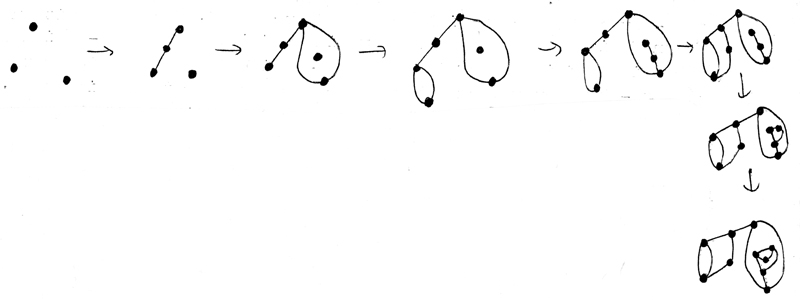
«Побеги» были изобретены совместно со студентом Майком Патерсоном и были освещены в колонке Scientific American в июле 1967 года. В ответ на письмо Гарднер отправил список вопросов, начинавшийся с вопроса «Что обозначает H в имени John H. Conway?». После каждого вопроса Гарднер оставил на листе много места, чтобы вписать ответ.
Ответ Конвея:
Хортон. А зачем так много места-то оставил? Ты думал, это будет нечто вроде Hog- ginthebottomtofflinghame-Frobisher-Williamss-Jenkinson?
Гарднер также интересовался деталями происхождения игры. «Я предсказываю, что эта игра станет настолько общепринятой и известной, что для истории будут интересны детали её создания,- писал Гарднер. – Не мог бы ты рассказать о них подробнее? Ты рисовал каракули на лекции (если да, то какой?) Или за кружкой пива?»
Мы рисовали каракули после чаепития в общей комнате департамента, пытаясь изобрести игру для карандаша и бумаги. Это было уже после того, как я провёл полный анализ одной старой игры, в которой были точки, но не было добавления новых – так что у неё не было «побегов». Она произошла от одной довольно сложной игры со складыванием марок, которую Майк Патерсон превратил в игру для карандаша и бумаги, и мы пытались модифицировать её правила. И Майк сказал – почему бы не добавить точку в середине? И сразу все остальные правила были отброшены, начальная позиция упрощена до n точек (изначально – 3), и побеги начали отрастать…
На следующий день в неё, казалось, играли все. За кофе или чаем группки людей рисовали глупые или очень сложные рисунки из побегов. Некоторые уже занимались этим на бутылках Клейна и т.п., а один математик размышлял о многомерном варианте игры. Листочки с партиями можно было найти в совершенно неожиданных местах.
Как только я пытаюсь кого-нибудь с ней познакомить, то оказывается, что он о ней уже где-то слышал. Даже мои дочки 3 и 4 лет играют в неё – хотя у них я обычно выигрываю.
И Конвей не останавливался. Следующее письмо было озаглавлено:
ВАЖНО! ПРОРЫВ В ПОБЕГОЛОГИИ!

Именованные позиции: мокрица, жук, таракан, серёжка, скорпион
Сегодня уже существует «Международная ассоциация игры в побеги» [The World Game of Sprouts Association], которая «посвящена изучению реальности побегов» и «серьёзному исследованию игры». Она проводит ежегодные онлайн-чемпионаты. В них могут участвовать только люди, поскольку компьютерный анализ игры за эти годы вдохновил некоторых написать ботов для игры. Конвей недавно узнал об этой ассоциации, но ему уже давно было известно о существовании компьютерных программ, играющих в игру.
Это было грустным известием. Компьютеры использовались для решения ряда открытых проблем. Они могли решить проблемы, существовавшие по 100 лет. Мы хотели изобрести игру, в которую было бы трудно играть компьютеру.
В начале 90-х три учёных из Лаборатории Белла и Университета Карнеги-Меллон написали работу «Компьютерный анализ игры в побеги», в которой анализировались выигрышные стратегии вплоть до n=11. «После 11 точек их программа не смогла справиться со сложностью игры»,- писал Гарднер для своих читателей. Через пару десятилетий два французских студента, решивших побить рекорд, написали программу GLOP (в честь французского персонажа комиксов Pif le chien, говорившего glop всякий раз, когда он испытывал удовлетворение). Они защитили докторскую по этой теме, и утверждают, что нашли выигрышные стратегии вплоть до n = 44. Конвей был очень заинтересован и удивлён этим:
Сильно сомневаюсь. Они утверждают, что совершили невозможное. Если бы кто-нибудь утверждал, что изобрёл машину, выдающую пьесы не хуже Шекспира – вы бы им поверили? Это очень сложно, и всё тут. Это как учить свиней летать. Но мне было бы интересно взглянуть на их работу.
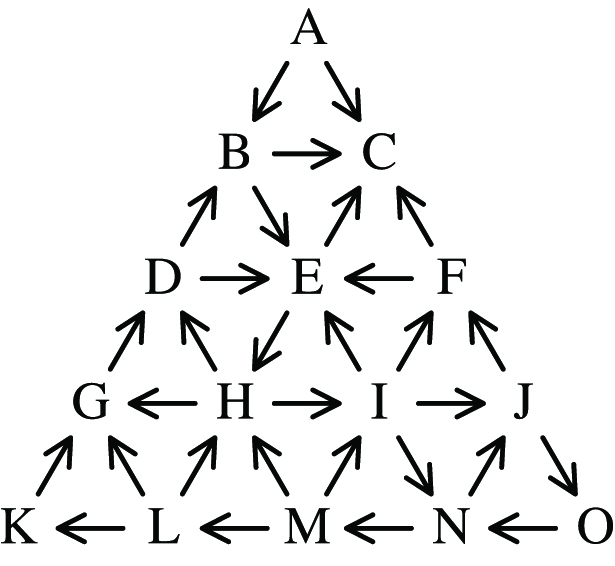
Ещё один пример гениальности Конвея – игра «Автомобильные пробки», в которой выдуманная страна имеет треугольную карту, а города представлены буквами. Все буквы являются первыми буквами названий реальных городов — Aberystwyth, Oswestry и Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch.
Подозреваю, что Конвей изобрёл игру только для того, чтобы лишний раз иметь возможность произнести название города Llanfairpwllgwyngyllgogerychwyrndrobwllllantysiliogogogoch. Он видел его на табличке на ж/д станции и на городской площади. Интересно, что эти знаки отличались на одну букву. А что касается игры, то её вопрос был – какой первый шаг должен сделать игрок?

В игре «Пробки» четыре игрока начинают с Aberystwyth (A), Dolgellau (D), Ffestiniog (F) и Merioneth (M). Они по очереди передвигаются по односторонним улицам между городами. Игра заканчивается, когда все игроки застревают в Conwy , из которого нет выхода. Проигрывает тот, чей ход должен был быть следующим.
Все эти игры поставляли данные для теории сюрреальных чисел Конвея. Лучшими подопытными игроками были его собственные дочки, Сьюзи и Рози, 7 и 8 лет.
По счастливой случайности, в этот период (около 1970), чемпион британии по Го, Джон Даймонд, учился в Кембридже. Он основал общество Го и постоянно играл в эту игру в общей комнате. Даймонд, сейчас являющийся президентом Британской ассоциации го, не помнит, чтобы хоть раз играл с Конвеем. Конвей обычно стоял рядом, смотрел на доску и размышлял над ходами игроков.
Конвей вспоминает:
Они обсуждали свои ходы за игрой, а непрошенные советчики вокруг галдели: «Почему ты так глупо сходил?». А эти плохие ходы для меня выглядели так же, как хорошие. Я никогда не понимал го. Но я понял, что к концу она разбивается на несколько игр – внутри одной большой игры были малые игры в разных частях доски. И это подвигло меня к разработке теории сумм партизанских игр.
А это, в свою очередь, подвигло его на ещё большее пристрастие к играм. У него с собой всегда были все нужные аксессуары, чтобы можно было неожиданно обрушиться на соперника. В его кожаном пенале всегда были кубики, шашки, доска, бумага, карандаши, верёвка, и несколько колод карт. Карточные игры и трюки ему удавались. Его анализ игр эволюционировал от простых до составных игр, до случаев, когда игрок одновременно играл в несколько игр сразу (иногда, например, шахматы, го и игра «Domineering») – и игрок выбирал, в какой из игр ему сходить. А он заполнял бумажные рулоны анализом этих игр. Как он рассказал репортёру журнала Discover:
Меня ждал удивительный сюрприз – я понял, что существует аналогия между моими записями и теорией вещественных чисел. А затем я понял, что это не аналогия – это действительно были вещественные числа.
И всё это развивалось, чтобы в результате стать сюрреальными числами – самым большим расширением множества вещественных чисел. Название им дал компьютерный специалист из Стэнфорда Дональд Кнут. И с тех пор Конвей уже не беспокоился о трудоголике профессоре Фрэнке Адамсе и о том, чтобы угодить ему и его коллегам. Он понял, что это открытие, пришедшее из «глупых игр», относилось уже к серьёзной математике. После того, как за один период в 12 месяцев он придумал сюрреальные числа, изобрёл игру «Жизнь» и открыл группы Конвея, он принял «клятву»: «И да закончишь ты волноваться и чувствовать вину, и да будешь делать то, что угодно тебе». Он сдался своему природному любопытству, шёл туда, куда оно его вело — хоть к развлечениям, хоть к исследованиям, хоть вообще в какое-то нематематическое место.
Гарднер суммировал теорию сюрреальных чисел, как «Винтажный Конвей: глубокий, инновационный, волнующий, оригинальный, блестящий, остроумный и отличающийся Кэрролловской игрой слов. И на тривиальном фундаменте Конвей строит огромное и фантастическое здание. Но чему оно посвящено?
Конвей в работе под названием „Все числа, большие и малые“, ставит вопрос проще: есть ли польза у этой структуры?
»Она находится на границе развлечений и серьёзной математики,- говорит американский математик венгерского происхождения Пол Халмос. – Конвей понимает, что её не назовут великой, но может попытаться убедить вас, что она именно такая". Напротив, Конвей верит, что сюрреальные числа – великая вещь, безо всяких «может». Он просто разочарован, что они пока не привели к ещё более великим вещам.
И на какое место они ставят его на пути древнего интеллектуального путешествия к красоте и правде? Конвей видит себя членом оркестра на параде, марширующего по улицам времени. В топ-10 газеты Observer Конвей упомянут среди математиков, чьи открытия изменили мир. Но попробуйте обсудить с ним этот список, или же другой список, в котором он недавно нашёл себя – в книге Клиффорда Пиковера «Чудеса чисел», под названием «десять самых влиятельных математиков нашего времени»… Он сразу же возразит:
С одной стороны, приятно. Я могу быть одним из известнейших математиков нашего времени – но это не то же самое, что быть лучшим. И это, скорее всего, из-за «Жизни». Но это смущает меня. Люди могут подумать, что я отстаю от лучших. Но это не так. И вообще, что ещё меня смущает, что в этих списках нет Архимеда или Ньютона.
Конвей считает Архимеда отцом математики. Именно он понял вещественные числа, и был первым, рассчитавшим число ? и ограничившим его сверху 3 1?7, а снизу — 3 10?71. Но в рейтинге Observer на первом месте идёт Пифагор. Если он и не лучший, то известный более других, в основном благодаря теореме его имени. И обычно в этих списках присутствуют Эйлер, Гаусс, Кантор, Эрдёш. Конвей идёт в конце, за ним идут Перельман и Тао.
Юношеская пора Конвея пришлась на сексуальные 70-е и неумеренные 80-е. В 80-х он развёлся с первой женой и женился на математике Ларисе Куин, начав новую семью. Стал членом Королевского общества и профессором Кембриджа. А затем перевёлся в Принстон в 1987-м. Пока ещё мы слишком близко находимся к Перельману, Тао и Конвею, чтобы правильно оценить их вклад в науку – особенно, каким образом их абстрактные теории смогут пригодиться на практике. Этот анализ займёт много времени.
Интересным исключением стал Джон Нэш, коллега Конвея в Принстоне, про которого написана книга и снят фильм «Игры разума». Нэш сделал вклад в теорию игр, моментально пригодившийся в эволюционной биологии, бухгалтерском деле, политике, военной теории и рыночной экономике, что и привело к получению им Нобелевской премии по экономике. С точки зрения Конвея, работа, заслужившая Нэшу нобелевку, была менее интересной, чем Теорема Нэша о регулярных вложениях (любое Риманово многообразие можно изометрически включить в Евклидово пространство). Конвей нацелился на получение премии Абеля («Нобель для математиков»). Он выиграл кучу других призов, но с премией Абеля пока ничего не выходит.
Да и практическое приложение его работы ещё предстоит открыть. Немногие сомневаются в том, что хотя бы что-нибудь из его творений сможет найти применение. Например, сюрреальные числа. «Сюрреальные числа найдут применение,- говорит его коллега, Питер Сарнак. – Вопрос только в том, какое и когда». Сарнак вообще восхваляет Конвея. «Конвей – соблазнитель»,- говорит Сарнак, имея в виду талант Конвея как учителя и толкователя, будь то занятия со студентами, математический лагерь, лекция на частной вечеринке или его альков в общей комнате Принстона.
Его всегда можно найти в этом алькове, где он не занят работой. И хотя он надеется ещё наткнуться на другие «горячие» темы вроде сюрреальных чисел, чаще он играется с любимыми тривиальностями. Он никогда не стесняется того, чтобы поймать незнакомца и начать заваливать его своими интересами. Один из недавних – "теорема свободы воли", в которой, по его мнению, заинтересован каждый человек. Она разработана за десять лет совместно с коллегой Саймоном Коченом, и формулируется через геометрию, квантовую механику и философию. Простая формулировка звучит так: если у физиков есть свобода воли при проведении экспериментов, то она есть и у частиц. И это, по их мнению, объясняет, почему у людей вообще есть свобода воли. Это не замкнутый круг, а больше замкнутая спираль, которая поддерживает сама себя, но раскручивается и становится всё больше.
Но обычно он более всего увлечён числами. Он их поворачивает, переворачивает, выворачивает и смотрит, как они себя ведут. А более всего он ценит знание и хочет узнать всё про Вселенную. Обаяние Конвея идёт от его желания поделиться своей тягой к знаниям, распространить это увлечение и связанную с ним романтику. Он упрямо, упорно стремится объяснить необъяснимое, и даже когда оно остаётся необъяснённым, ему удаётся вдохновить аудиторию, скреплённую неудавшейся попыткой, чувствующую себя частью одной команды, удовлетворённой тем, что они смогли пофлиртовать с проблеском понимания.
Комментарии (6)

olekl
28.12.2015 15:04Что-то я в «пробках» не понял — а что мешает игроку бесконечно ходить по кругу, например, D -> E -> H?

valemak
28.12.2015 16:51Игроки, которые начинают с точек A, D и F уже на первых ходах будут мешать друг другу ездить по кругу. Игроку, начинающему с точки M ещё надо выехать на подходящую траекторию.
По всей видимости, граф подобран так, что непересекающееся периодическое движение для всех четырёх игроков невозможно. Даже если они будут играть кооперативно, не удастся синхронизировать их движение так чтобы они друг другу не мешали.

hmpd
28.12.2015 19:47Простая формулировка звучит так: если у физиков есть свобода воли при проведении экспериментов, то она есть и у частиц. И это, по их мнению, объясняет, почему у людей вообще есть свобода воли.
А Толстой в «Войне и мире» довольно убедительно доказывал, что свобода воли у человека отсутствует ))
Спасибо за статью. Теперь запомню Конвея не только как создателя «Жизни»


Sirion
Прочитав название статьи, даже как-то забеспокоился о здоровье товарища Конвея. Не сразу понял, что имеется в виду окончание перевода.