А не замахнуться ли нам на Эдсгера нашего Дейкстру?

В первой части мы описали способ ранжирования симметрично связанных объектов (узлов неориентированного графа) относительно заданного направления. Для каждого объекта (узла) вычисляется потенциал (лапласиана), который определяет его положение относительно заданных источника и цели. В данной статье мы покажем, как потенциалы узлов упрощают задачу поиска кратчайших путей (оптимальных маршрутов). А также как меняются сами потенциалы при изменении внешних условий.

В общем случае минимизируемая величина — это необязательно расстояние, — весами ребер графа могут быть стоимости, штрафы, убытки, времена, — любые величины, которые можно складывать. Задача является классической, наиболее простой алгоритм поиска кратчайшего пути дал Э. Дейкстра аж в 1959 году.

Карта потоков

На основании вычисленных в предыдущей части потенциалов и заданных связностей/проводимостей (обратных расстояниям) можно нарисовать карту потоков. Вот ее вид:


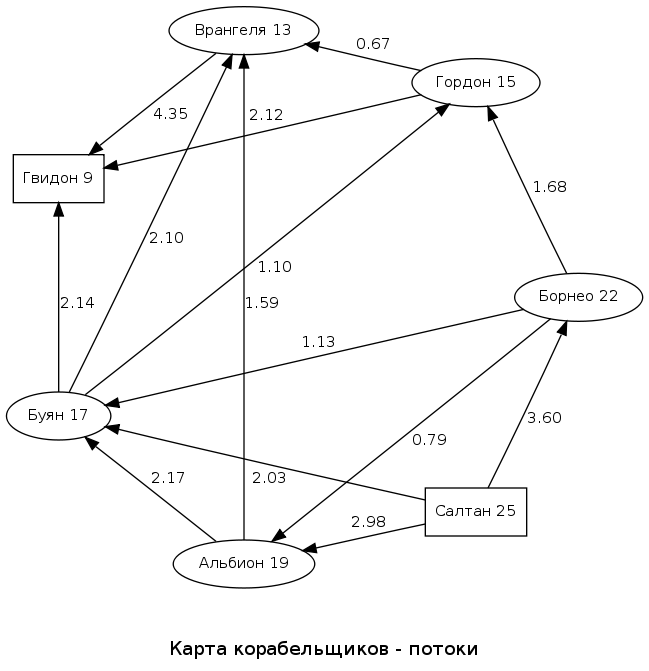
Источник (Салтан) и приемник (Гвидон) выделены квадратами. Рядом с названием узла (острова) округленное значение потенциала. Цифры рядом со стрелками отражают величину потока (разность потенциалов деленная на расстояние).

Если бы Салтан пошел на Гвидона армией, то ему бы пришлось распределять направления перемещения масс с учетом величин потоков, указанных на данной карте. Или если б Салтан был комаром фотоном или электроном — тогда бы он тоже полетел/поплыл по всем путям одновременно. Но в реальном мире рулят путешественники-одиночки с ненулевой массой, поэтому нам нужны не все пути, а как раз наоборот — один, но оптимальный.

Наличие потенциалов упрощает (ускоряет) построение оптимального пути. Есть два основных алгоритма — быстрый (но без гарантий оптимальности) и точный. Последний тоже быстрый (относительно классических), но медленнее первого.

Алгоритм Нео

Вспомним рекомендацию Нео — "если хочешь добраться ко сроку — плыви по максимальному потоку". Мы можем ей воспользоваться на основании приведенной карты.

Идея такая. Для каждого узла приведенного на рисунке графа (кроме исходного) надо оставить только входящую ветку и удалить все остальные. Это гарантирует однозначность маршрута от источника. Условием выбора входящей ветки будет максимальность потока.
Для того, чтобы обеспечить скорость работы алгоритма и не перебирать все узлы графа, надо начать с конечного (целевого) узла и двигаться от него по веткам с максимальным потоком в начало.

Согласно карте максимальный поток (4.35) на Гвидона идет с Врангеля — значит, оставляем ветку «Врангель-Гвидон» (включаем ее в путь).
Переходим по ветке на Врангеля. Максимальный поток на Врангеля (2.10) идет с Буяна — идем на Буян. С Буяна соответственно на Альбион, с Альбиона — на Салтана, путь построен. В нашем случае он действительно оптимальный (относительно сумм весов веток исходной карты расстояний) — повезло.

Достоинство данного способа — простота и быстрота построения пути. Мы перебираем только те узлы графа, которые входят в маршрут, то есть скорость работы алгоритма фактически пропорциональна длине оптимального пути (часто это намного меньше размера графа).
Минус — использованный принцип (максимальный поток) не гарантирует оптимальности маршрута. Можно построить карту, для которой «маршрут Нео» будет не самым оптимальным, хотя и близким к нему.

Алгоритм Дейкстры с ранжированием

Если нужен оптимальный алгоритм с гарантией, то придется считать расстояния для каждого узла. Данный способ похож на упомянутый в начале алгоритм Дейкстры, но использование потенциалов (упорядоченности узлов) позволяет выполнить данный расчет за линейное (относительно количества узлов графа) время.

Принцип остается тем же — нам надо определить (оставить) только одну входящую ветку для каждого узла (кроме исходного). Но теперь мы будем использовать точно рассчитанные для узлов длины путей (расстояния от источника) и оставлять ветки с минимальной длиной пути.

Начинаем с начала (остров Салтана) и далее по степени убывания потенциала перебираем каждый узел/остров. Использование порядка перебора узлов гарантирует, что при определении длины пути до текущего узла входящие в него ветки будут идти от уже посчитанных узлов.



Итак, поехали. Остров Салтана является источником, поэтому ему присваиваем нулевую длину пути — d(Салтана) = 0. У источника нет входящих веток (нечего обрезать), поэтому переходим к следующему — Борнео.

У Борнео только одна входящая ветка, поэтому для него сразу можно определить расстояние от источника d:
d(Борнео) = d(Салтана) + Вес пути (Борнео — Салтан) = 0 + 1 = 1

Идем далее на Альбион. В Альбион входит две ветки — от Салтана и от Борнео. Длина пути d для них уже известна, поэтому можно определить длину пути Альбиона для обеих веток: от Салтана — 2, через Борнео — 1+3 = 4. Оставляем минимальную (от Салтана) и присваиваем Альбиону расстояние от источника — d = 2.
Ненужные ветки либо помечаем как неактуальные, либо (если нам нужно построить минимальное дерево — остов графа) удаляем.

Следующий по порядку — остров Буян. У Буяна три входящих ветки. Определяем минимальную — эту будет ветка через Альбион и длина пути от источника до Буяна будет d(Альбион) + 1 = 2 + 1 = 3.

И так далее для всех островов. Последним будет остров Гвидона — на нем расчет пути заканчивается. Для определения оптимального пути двигаемся в обратном направлении от Гвидона до Салтана по актуальным входящим веткам.

В отличие от алгоритма Нео здесь нам приходится пройтись по всем узлам графа и для каждого рассчитать оптимальное расстояние от источника. Но зато мы можем сразу построить дерево (остов) достижимости всех узлов графа из источника (у такого дерева интересные свойства, но это отдельная тема).

Достоинство данного алгоритма по сравнению с классическим Дейкстрой — он однопроходный (сложность ~n). Путь до узла считается только один раз и больше не пересчитывается — следствие упорядоченности узлов графа. Соответственно скорость данного алгоритма выше. Но за все приходится платить. Здесь платой являются начальные затраты на расчет потенциалов (матрицы потенциалов) узлов.

Можно было бы назвать данный алгоритм «улучшенным алгоритмом Дейкстры», если бы у Дейкстры уже не было n-го количества улучшений. Назовем его поэтому «алгоритмом Дейкстры с предварительным ранжированием».

Салтан может отправляться в путь — Альбион (2) > Буян (3) > Врангеля (5) > Гвидон (6). Привет князю.

Устойчивость к переменам

Как известно, устойчивость системы определяется ее реакцией на внешнее воздействие. Если при небольшом изменении входных параметров системы получаем большие изменения выходных — то это слабо устойчивая система. Применительно к алгоритмам на графе это означает, что устойчивый алгоритм не должен требовать полного пересчета в случае изменения, например, величины связности одного из ребер графа.
Достоинство использования матрицы потенциалов в том, что изменение входных требований можно учесть явными формулами — повторного обращения лапласиана не требуется.

Что может измениться? Ну, например, на обратном пути надо заехать из Гвидона в Борнео. Какой маршрут оптимальный? Если есть матрица потенциалов, то пересчет прост — надо посчитать потенциалы нового направления и выполнить описанный выше алгоритм расчета оптимального пути.

В нашем случае важна только разность потенциалов между узлами, поэтому значения потенциалов узлов при заданном источнике S и приемнике G можно считать по формуле:



Это аналог формулы (2.5) из предыдущей части. По данному выражению очень просто пересчитать потенциалы для нового маршрута (например, из Гвидона в Борнео).

Более сложная ситуация — изменилась проводимость (связность) одного из путей (у нас в городе каждой весной такая ситуация) — как это скажется на значениях потенциалов?

Изменение потенциала i-го узла при изменении связности ребра jk запишем как:



Отметим во избежание путаницы, что здесь под производной понимается симметричное возмущение, то есть



(В предыдущей части для возмущения мы использовали направленную производную, там варьирование было несимметричным: ).

Из выражения (2) видно, что для определения изменений потенциалов узлов нам надо научиться считать производные матрицы потенциалов . Эти же производные будут востребованы, если понадобится пересчитать значения матрицы потенциалов при изменении связности .

Смежные производные и потенциалы 3-го порядка

Возможны три ситуации в зависимости от пересечения множеств индексов i, j и k, l. Если индексы варьируемой переменной kl совпадают с индексами потенциала i j, то тут все просто — производная равна 0.



Если совпадает только один из индексов, то будем назовем такую производную смежной. Смежная производная потенциала 2-го порядка выражается через потенциал 3-го порядка:



Поскольку значение симметричного потенциала не зависит от порядка индексов, то видим, что что все смежные производные с одним и тем же составом индексов равны между собой:



Для нас важно, что потенциалы 3-х порядков могут быть выражены через матрицу потенциалов (то есть через потенциалы 2-го порядка) согласно тождеству:



Выражение (5) можно немного укоротить:



Здесь — скалярный (общий) потенциал, который можно рассматривать просто как множитель.
Избавимся в (5) от обозначений потенциала и оставим только индексы:



Дамы и господа, перед нами знаменитая Джоконда формула Герона, которая как известно, используется для нахождения площади треугольника. Да, потенциалы 3-го порядка тесно связаны с площадями фигур. Следствие того, что как уже отмечалось, потенциалы 2-го порядка не менее тесно связаны с квадратами расстояний.

Но вот как так получается, что производные каких-то потенциалов каких-то абстрактных графов вдруг оказываются связанными с формулами геометрии — загадка и маленькое чудо.

Итак, смежные (и симметричные) производные потенциалов (по связности) можно выразить через сами эти потенциалы.
Теперь мы можем посчитать, например, как изменится потенциал ветки «Борнео-Альбион» при изменении связности ветки «Салтан-Борнео». Согласно формуле нам нужны для этого потенциалы между всеми 3-мя узлами. Согласно матрице потенциалов имеем:

• «Салтан — Борнео» — 6.25,
• «Альбион — Борнео» — 8.36,
• «Салтан — Альбион» — 8.19.

Скалярный потенциал лапласиана равен 8.61.
Подставляя значения потенциалов в формулу (6) и (4), получаем значение изменения потенциала для единичного варьирования:



Так и есть, можете проверить.

Свободные производные потенциалов 2-го порядка

Под свободной производной мы понимаем такую, в которой индексы варьируемой связности не пересекаются с индексами потенциала. На самом деле это и есть наиболее общий случай, из которого должны следовать все остальные. Но именно поэтому выразить значение данной производной через значения потенциалов 2-го порядка оказалось не так-то просто (во всяком случае — мне).

Опуская подробности (укажем лишь, пожалуй, что выражения потенциалов одного порядка через другие удобно использовать тождество Доджсона, который по совместительству Льюис Кэрролл), приведем конечный ответ. Он совпал (и, конечно, стал сразу очевидным после того, как был найден) с выражением для площади четырехугольника (откуда тут площади — уже обсуждали, а почему четырехугольник — тоже понятно — у нас 4 независимых вершины графа). В индексных обозначениях:



(Мы тут довольно свободно используем обозначения, чтобы не загромождать общую структуру, — надеюсь, все понятно. Одинокая (и свободная) i — это скалярный потенциал).

Четырехугольник, площадь которого соответствует данной формуле, образуется вершинами i, j k, l. При этом вершины i, j (и соответственно j, k) должны быть противоположными.
Потенциалы — это квадраты длин диагоналей данного четырехугольника (ну и длинное же слово). Остальные потенциалы — квадраты длин сторон.

Круто. Я не понимаю, как и почему производные потенциалов связаны с площадями, но все равно спасибо за то, что формулы такие простые. (И, пользуясь случаем, — спасибо, Wolphram — нет-нет, да выручаешь).

Тождество (7) является пуантой наших усилий (тут бы надо сесть и не спеша над ним помедитировать. Но некогда).
Из него легко получить формулу Герона (6) и тождество (3), которое геометрически объясняется тем, что площадь отрезка равна 0 (в терминах геометрии это очевидно, а в потенциалах лапласиана — не сразу).

Теперь у нас есть формулы для всех видов производных. Можно, например, рассчитать изменение потенциала ветки «Альбион — Гвидон» при том же изменении связности «Салтан-Борнео» (для тех, кто захочет, ответ — 9.36).

Таким образом матрица потенциалов лапласиана (плюс скалярный потенциал) определяет и значения всех своих производных (а также потенциалов более высоких порядков). Данное свойство позволяет динамически поддерживать актуальность значений матрицы при изменениях связности ребер графа. Нам не надо обращать лапласиан, достаточно воспользоваться формулой площади четырехугольника (7) и вычислить новые значения потенциалов.

Резюме

Заканчиваем. В статье мы рассмотрели использование потенциалов для одной из классических задач — поиск кратчайшего пути. Матрица потенциалов позволяет упростить и ускорить алгоритм такого поиска. Это неплохой и полезный прикладной результат.

Но главное даже не в этом. Мы использовали данную задачу лишь как повод рассказать о лапласианах и о некоторых их замечательных свойствах. Показали, что представляет собой матрица потенциалов и как ее можно использовать. Увидели, как неожиданно проявляется связь между казалось бы различными областями математики. Пользуйтесь!